Cómo funciona la criptografía de curva elíptica en TLS 1.3

Un par de advertencias para el lector:

Para simplificar (tanto como sea posible) el proceso de explicación y exprimir el volumen de publicación, vale la pena hacer una reserva clave de inmediato: todo lo que escribimos sobre el lado práctico del problema es correcto para el protocolo TLS versión 1.3. Esto significa que, aunque su certificado ECDSA, si lo desea, funcionará con TLS 1.2, la descripción del proceso de protocolo de enlace, conjuntos de cifrado y puntos de referencia se basa en la última versión del protocolo TLS - 1.3. Como saben, esto no se aplica a la descripción matemática de los algoritmos que subyacen a la base de los sistemas criptográficos modernos.

Este material no fue escrito por un matemático o incluso un ingeniero, aunque ayudaron a allanar el camino a través de la jungla matemática. Muchas gracias al personal de Qrator Labs.

( E líptico C urve) D iffie- H ellman ( E phemeral)

Legado del siglo XXI Diffie-Hellman

Naturalmente, este tema no comienza con Whitfield Diffie y no con Martin Hellman. Alan Turing y Claude Shannon hicieron una gran contribución a la teoría de algoritmos y teoría de la información, así como al campo del criptoanálisis. Diffie y Hellman, a su vez, son reconocidos oficialmente por los autores de la idea de la criptografía de clave pública (también llamada asimétrica), aunque ahora se sabe que también se han logrado resultados serios en esta área en el Reino Unido. Sin embargo, permanecieron en secreto durante mucho tiempo, lo que hace que los dos caballeros mencionados en los subtítulos sean pioneros.

Que exactamente

Esto puede parecer divertido, pero hasta el 6 de noviembre de 1976, no había conocimiento disponible sobre los sistemas criptográficos de clave pública. Whitfield Diffie y Martin Hellman (y, de hecho, Ralph Merkle): matemáticos, ingenieros informáticos y entusiastas, así como criptólogos, fueron los primeros en proponer un concepto adecuado.

Durante la Segunda Guerra Mundial, la criptografía ayudó a mantener la información en secreto, y el criptoanálisis ayudó a revelarla. Estados Unidos y el Reino Unido se consideraban los más avanzados en el campo de la criptografía. Estos dos países incluyeron algoritmos criptográficos en la sección de armas y vetaron sus exportaciones. Al mismo tiempo, el cifrado disponible y destinado para uso comercial o doméstico se ha aflojado en estos países. Por esta razón, los investigadores británicos que trabajan en un esquema de distribución de claves asimétricas en el Centro de Comunicaciones del Gobierno (GCHQ) y que desarrollan un concepto similar no fueron reconocidos por la comunidad hasta 1997, cuando las restricciones existentes en los algoritmos criptográficos y su descripción perdieron todo significado y, en general moralmente anticuado

Volviendo a nuestro par de inventores, ¿qué revolucionaron exactamente Diffie y Hellman?

Para explicar esto, echemos un vistazo a la ilustración de la publicación original, que refleja a la perfección el salto gigante en la comprensión de cómo puede funcionar la criptografía, incluso aunque solo sea inicialmente teóricamente:

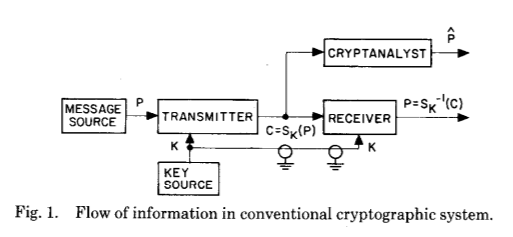
Y ahora para lo siguiente:

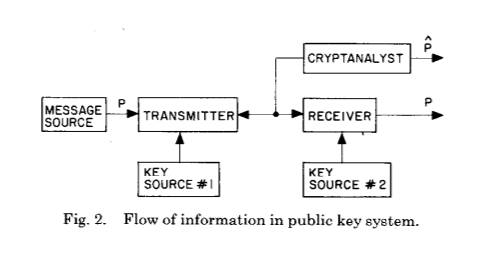
Estas dos imágenes muestran la principal innovación de Whitfield Diffie y Martin Hellman después de siglos de desarrollo de criptografía y criptoanálisis: el establecimiento de un secreto común como resultado de cálculos de cierto tipo.

Veamos otra imagen de Wikipedia, donde se usan diferentes colores como secretos:



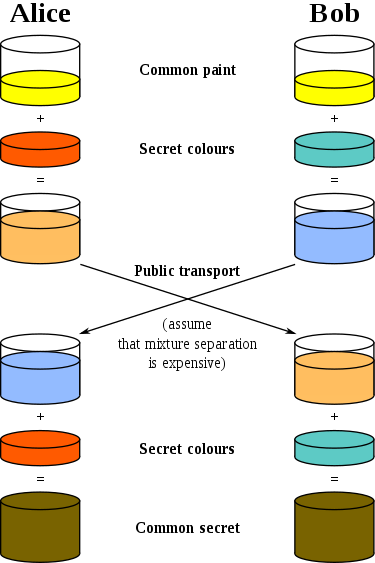
Ella también explica bien lo que está sucediendo. Antes de la innovación de Diffie y Hellman, solo había una clave común en forma de un esquema de establecimiento de clave común: se usaba para cifrar y descifrar un mensaje. Si desea transferir dicha clave al segundo lado, debe transmitirse a través del canal originalmente protegido. Inmediatamente se aclaran todas las limitaciones de dicho esquema: necesita un canal de comunicación seguro (desde la escucha), no puede usar la misma clave más de una vez e, idealmente, la longitud de la clave debe corresponder a la longitud del mensaje.

Claude Shannon, en su trabajo desclasificado más adelante, "Teoría de la comunicación en sistemas secretos", demostró que todos los cifrados teóricamente irrompibles deben tener las mismas propiedades que un bloque de cifrado único, también conocido como el cifrado Vernam, por el nombre del creador de este algoritmo de cifrado de flujo polialfabético aditivo.

Y nuevamente, echemos un vistazo a la publicación científica original:


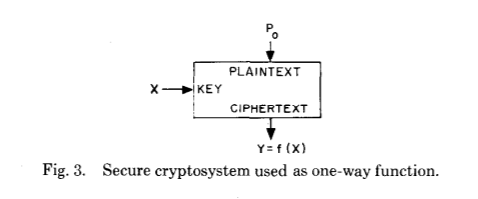
Antes de continuar, hagámonos una pregunta obviamente simple: ¿cómo podrían dos personas, incluso muy desarrolladas intelectualmente, llegar a algo tan innovador en el campo aplicado, especialmente dados los enormes éxitos de la guerra? Probablemente debido a la combinación de las siguientes áreas que se estaban desarrollando activamente en ese momento:

• Teoría de la información formulada por Claude Shannon;
• La teoría de algoritmos , que fue influenciada, entre otros, por Alonzo Church, John von Neumann y Alan Turing;
• Y, sobre todo, la teoría de la computabilidad , basada principalmente en el trabajo de Turing.

Podemos decir que todas estas áreas se han desarrollado y madurado alrededor del mismo período del siglo XX. Diffie y Hellman también mencionaron a Claude Shannon como una figura que influyó en su trabajo más que otros.

El concepto de "Seguridad Universal" de Arjen Lenstra muestra cuánta energía se debe gastar en "piratear" un sistema criptográfico simétrico con claves de diferentes longitudes. Resultó que para descifrar la clave de 228 bits del algoritmo basado en curvas elípticas, se necesita tanta energía como sea suficiente para calentar toda el agua de la Tierra hasta el punto de ebullición. Sin embargo, esta afirmación es correcta solo si consideramos algoritmos bien conocidos y usamos equipos modernos, ya que, estrictamente hablando, son posibles algoritmos o equipos más eficientes, pero su existencia aún no se conoce. La clave de 228 bits para el algoritmo EC para piratear la complejidad es comparable a la clave de 2380 bits en RSA, pero más sobre eso más adelante. En esta comparación, las claves RSA y EC se utilizan en un criptosistema asimétrico, se pueden considerar equivalentes a una clave de 128 bits en un esquema simétrico.

Es fácil imaginar que algo "difícil de calcular" requerirá una gran cantidad de tiempo y energía para calcular. Tendemos a pensar que las computadoras pueden "contar cualquier cosa", pero resulta que esto está lejos de ser verdad.

En primer lugar, hay ejemplos de problemas sin solución, como el problema de detención. Sin embargo, en el campo de la criptografía, tales tareas no se utilizan.

En segundo lugar, si consideramos el tiempo de ejecución requerido por un algoritmo particular, entonces puede ser arbitrariamente grande. Esto es exactamente lo que usa la criptografía. Una tarea se considera computacionalmente "simple" si el tiempo requerido para que el algoritmo correspondiente funcione depende del tamaño de los datos de entrada (medidos en bits) como un polinomio: $$$T (n) = O (n ^ k)$ por algo positivo $$$k$ . En la teoría de la complejidad computacional, tales problemas forman una clase de complejidad P. Si el tiempo de ejecución del algoritmo crece más rápido que un polinomio, por ejemplo, exponencialmente, dicha tarea se considera computacionalmente "difícil".

La clase de complejidad P incluye tareas para las cuales existe un algoritmo determinista que funciona en tiempo polinómico. Otra clase de complejidad es NP (en la que, presumiblemente, existen problemas "difíciles"), que es un problema de solución, es decir, un problema que requiere una respuesta de "sí" o "no", cuya corrección puede verificarse, es decir, para proporcionar pruebas de la corrección de la solución. en tiempo polinomial. ¿Ves la palabra "prueba" aquí? Este es el lugar en el que pasamos a funciones unilaterales cuyo problema de inversión pertenece a la clase de complejidad NP.


Publicado por: xkcd

(Funciones unidireccionales (con entrada secreta))

Por definición, una función unidireccional es una función que es fácil de calcular para cualquier entrada, pero difícil de invertir, es decir, obtener la entrada original solo con el resultado. "Fácil" y "difícil" se refieren a la teoría de la complejidad computacional mencionada anteriormente. Es interesante que no se haya probado la existencia de funciones unidireccionales (matemáticamente), ya que una prueba rigurosa de su existencia también probaría la desigualdad de las clases P y NP, uno de los problemas del milenio y un problema abierto urgente, cuya solución promete un avance algorítmico. Por lo tanto, es necesario tener en cuenta que casi toda la criptografía moderna se basa en hipótesis no comprobadas.

En su publicación original, Diffie y Hellman presentan una nueva generación de funciones unidireccionales, llamándolas "funciones unidireccionales con una entrada secreta", en inglés, función trampilla. ¿En qué se diferencian de las funciones unidireccionales?

Veamos su explicación original:

En un sistema criptográfico con una clave pública, el cifrado y el descifrado se realizan mediante varias claves, E y D, respectivamente, de modo que calcular D desde E es prácticamente imposible (por ejemplo, requerir $$$10 ^ {100}$ instrucciones). La clave de cifrado E puede divulgarse públicamente sin comprometer la clave D. Esto permite que cualquier usuario del sistema envíe un mensaje a cualquier otro usuario, cifrado de tal manera que solo el destinatario esperado pueda descifrarlo. <...> La tarea de autenticación, tal vez, es un problema de telecomunicaciones más serio para las transacciones comerciales, en comparación con la distribución de claves, ya que (la autenticación) se encuentra en el corazón de cualquier sistema que funcione con contratos y facturación para el pago.

Por lo general, los caracteres criptográficos Alice y Bob se utilizan para explicar los principios del funcionamiento del sistema criptográfico (se esfuerzan por una comunicación segura). Alice y Bob acuerdan elegir primos grandes $$$n$ y $$$g$ tal que $$$1 <g <n$ . Esta elección afecta la seguridad de todo el circuito. Numero $$$n$ llamado un módulo debe ser simple; Además, el número $$$(n-1) / 2$ También debería ser simple, pero $$$g$ debe ser la raíz primitiva en el módulo de grupo de residuos $$$n$ ; ademas $$$n$ debe ser lo suficientemente grande: al menos 512 bits en representación binaria. Además, el protocolo Diffie-Hellman se puede describir en cinco simples pasos:

1. Alice recoge $$$x$ (primo grande) y calcula $$$X = g ^ x \ bmod n$
2. Bob recoge $$$y$ (también una gran prima) y calcula $$$Y = g ^ y \ bmod n$
3. Alice envía $$$X$ Bob, Bob envía $$$Y$ Alice ( $$$x$ y $$$y$ cada uno de ellos sigue siendo un secreto)
4. Alice calcula $$$k = Y ^ x \ bmod n$
5. Bob está calculando $$$k '= X ^ y \ bmod n$

Como resultado, Alice y Bob obtienen el mismo resultado en la construcción. $$$k = k '$ - Un secreto compartido.

Entonces, una función unidireccional con una entrada secreta es una función unidireccional que se puede revertir al tener una información especial llamada "entrada secreta". Suena simple, pero en la práctica, encontrar esa función resultó ser una tarea no trivial: el primer método decente resultó ser el progenitor de toda una familia de algoritmos basados ​​en una clave pública llamada RSA por los nombres de sus creadores: Ron Rivesta, Adi Shamira y Leonard Adleman.

RSA

En RSA, la complejidad de invertir una función se basa en el hecho de que la factorización (factorización de un número) lleva mucho más tiempo que la multiplicación o, más precisamente, se puede argumentar que no se encontró ningún método para factorizar números grandes en tiempo polinómico en una computadora clásica, aunque no fue Está comprobado que dicho algoritmo no puede existir.

En RSA, como en cualquier otro sistema criptográfico con una clave pública, hay dos claves: pública y privada. El algoritmo RSA toma un mensaje de entrada representado por una cadena de bits y le aplica una operación matemática (elevando a un módulo de potencia un gran número) para obtener un resultado indistinguible de aleatorio. Para el descifrado, se toma el resultado y se realiza una operación similar para recibir el mensaje original. En la criptografía asimétrica, el cifrado se realiza con una clave pública y el descifrado con una clave privada.

¿Cómo es esto posible? Debido al hecho de que los valores utilizados pertenecen a un grupo cíclico finito (el conjunto de enteros con multiplicación en aritmética modular). Las computadoras no funcionan muy bien con números arbitrariamente grandes, pero la propiedad del grupo cíclico es "envolvente": un número mayor que el máximo permitido se "ajusta" a un valor del conjunto permitido. Esto nos permite usar claves con una longitud de "no más que" un cierto número de bits. En la criptografía basada en curvas elípticas, también se usan grupos cíclicos (multiplicativos), pero se construyen de manera ligeramente diferente, como veremos más adelante.

A un nivel muy primitivo, todo lo que hace RSA es tomar dos primos grandes, multiplicándolos para obtener el llamado módulo. Todos los demás números con los que se realizarán las operaciones deben estar entre cero y el valor del módulo. El módulo en sí se convertirá en parte de la clave pública: su longitud determina la longitud de la clave. La segunda parte de la clave pública es el número elegido entre cero y el valor de la función Euler (las implementaciones RSA modernas usan la función Carmichael en lugar de Euler) del módulo, con algunas restricciones adicionales. Finalmente, puede calcular la clave privada resolviendo la ecuación modular. Para cifrar el mensaje, tomamos el número que representa el mensaje y simplemente lo elevamos a la potencia igual al valor de la clave pública, y descifrarlo: para recibir el mensaje original, elevarlo a la potencia igual al valor de la clave privada. Debido a la naturaleza cíclica del grupo, obtenemos el mismo significado.

Hoy, RSA tiene dos problemas principales, uno de los cuales es consecuencia del otro. A medida que crece la longitud de la clave, la complejidad no crece tan rápido como nos gustaría. Esto se debe a que existe un algoritmo de factorización subexponencial (pero aún superpolinómico ). Por lo tanto, para mantener el nivel de protección necesario, la longitud de la clave RSA debería crecer algo más rápido que la de la clave ECC. Por esta razón, las longitudes de clave RSA más comunes hoy en día son bastante grandes: 2048 y 3072 bits.

Un poco más adelante veremos en figuras específicas cómo la longitud de la clave afecta el rendimiento final del sistema criptográfico al comparar los certificados firmados por Let's Encrypt RSA y ECDSA.

E líptica C urve A lgoritmos de la ignición digital S

En busca de funciones más confiables con una entrada secreta, a mediados de los años 80, los criptógrafos utilizaron una rama de las matemáticas dedicada a las curvas elípticas.

Sería demasiado difícil describir todos los detalles de la criptografía basada en curvas elípticas en un texto, por lo que no haremos esto. En cambio, veamos una función de entrada secreta unidireccional construida sobre la base de curvas elípticas y el problema del logaritmo discreto.

Hay una gran cantidad de materiales de revisión e introducciones más detalladas en esta área de la criptografía. Nos gustaría señalar "ECC: una introducción amable" de Andrea Corbellini, especialmente si está interesado en el dispositivo.

Nosotros, en este material, estamos interesados ​​en una explicación mucho más "simple".
Una curva elíptica se define mediante una ecuación que se ve así: $$$y ^ 2 = x ^ 3 + hacha + b$ .

El segundo objeto es un subgrupo cíclico sobre un campo finito. Los siguientes parámetros se utilizan en el algoritmo ECC:

• Número primo $$$p$ , que determina la dimensión del campo final;
• Las probabilidades $$$a$ y $$$b$ ecuaciones de curva elíptica;
• Punto base $$$G$ generar el subgrupo ya mencionado;
• Orden $$$n$ subgrupos;
• Cofactor $$$h$ subgrupos

Como resultado, el conjunto de parámetros para nuestros algoritmos está representado por seis $$$(p, a, b, G, n, h)$ .

Los puntos de una curva elíptica pertenecen a un campo finito. $$$\ mathbb {F} _p$ donde $$$p$ Este es un número primo bastante grande. Entonces, tenemos muchos módulos enteros $$$p$ donde son posibles operaciones como sumar, restar, multiplicar, tomar lo contrario. La suma y la multiplicación funcionan de manera similar a cómo lo describimos en términos de la aritmética modular de la sección RSA (envoltura).

Como la curva es simétrica respecto al eje x, para cualquier punto $$$P$ podemos tomar $$$−P$ y obtener el punto opuesto a él. Inmediatamente estipulamos que el punto $$$−O$ corresponde a cero, es decir $$$−O$ será simple $$$O$ .

La adición de puntos en una curva se define de modo que, conociendo los puntos $$$P$ y $$$Q$ , podemos dibujar una línea que pase por ambos puntos, así como un tercero: $$$R$ para que $$$P + Q = -R$ y $$$P + Q + R = 0$ .

Echemos un vistazo a la ilustración ilustrada de Mark Hughes :

Vemos una línea recta estirada a lo largo de la superficie del toro. La línea intersecta dos puntos seleccionados al azar en la curva.



Para encontrar $$$R$ , dibujamos una línea desde el primer punto seleccionado $$$P$ al segundo $$$Q$ continuando la línea hasta que cruza la curva en el tercer punto $$$-R$ .

Después de la intersección, refleje el punto relativo al eje de abscisas para encontrar el punto. $$$R$ .

La multiplicación por un escalar se determina obviamente: $$$n \ cdot P = P + P + P + \ dots + P$ .

La función unidireccional con una entrada secreta en este caso se basa en el problema del logaritmo discreto para las curvas elípticas, y no en la factorización, como es el caso con RSA. El problema del logaritmo discreto en este caso se formula de la siguiente manera: si se conoce $$$P$ y $$$Q$ , entonces cómo encontrar $$$k$ tal que $$$Q = k \ cdot P$ ?

Tanto el problema de factorización (RSA subyacente) como el logaritmo discreto para curvas elípticas (que son la base de ECDSA y ECDH) se consideran difíciles; en otras palabras, no hay algoritmos para resolver estos problemas en tiempo polinómico para una longitud de clave determinada.

Aunque, por lo general, sería bombardeado con trapos sucios (en el mejor de los casos) para mezclar algoritmos de distribución de firma (ECDH) con firma (ECDSA), todavía tengo que explicar cómo funcionan juntos.Un certificado TLS moderno contiene una clave pública, en nuestro caso, de un par generado utilizando un algoritmo basado en curvas elípticas, generalmente firmado por alguna organización autorizada. El cliente verifica la firma del servidor y genera un secreto compartido. Este secreto se usa en un algoritmo de cifrado simétrico como AES o ChaCha20. Sin embargo, los principios básicos siguen siendo los mismos: acuerde un conjunto (seis) de parámetros, obtenga un par de claves, donde la clave privada es un entero seleccionado al azar (un factor de$$Q = k ⋅ P ), y la clave pública es un punto en la curva. Los algoritmos de firma usan un punto base$Q=k\cdot P$$$G , que es un generador de un subgrupo de orden$G$$$$n$ ( $$n es un primo grande), entonces$n$$$n ⋅ G = 0 , donde 0 es el elemento neutral del grupo. La firma prueba que se establece una conexión segura con una parte autenticada: un servidor que tiene un certificado TLS (clave pública) firmado por una organización autorizada para un nombre de servidor determinado.$n\cdot G=0$

(EC) DH (E) + ECDSA = forma moderna de apretón de manos

En la versión 1.3 moderna de TLS, el cliente y el servidor generan un par de claves sobre la marcha, estableciendo una conexión. Esto se llama la versión "efímera" del algoritmo de intercambio de claves. Las bibliotecas TLS más populares son compatibles con tal versión de protocolo. En su mayor parte, hoy se utiliza la curva elíptica Edwards 25519 , propuesta por Daniel Bernstein Jr. (djb), que proporciona un nivel de protección de 128 bits. Desde 2014, esta curva ha estado disponible para crear pares de claves en la biblioteca openssh. Sin embargo, a fines de 2019, los navegadores aún no establecen una sesión TLS con servidores que utilicen la clave pública del algoritmo de firma EdDSA.

Veamos cómo funciona todo en TLS 1.3.

En la última versión del protocolo, los mecanismos de distribución de claves se limitan a (EC) DH (E): x25519 es la función más común para obtener una clave compartida; es compatible con la mayoría de las bibliotecas TLS de navegador y servidor. El conjunto de cifrado consta de solo tres entradas: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 y TLS_CHACHA20_POLY1305_SHA256. Para aquellos de ustedes que están familiarizados con cómo se nombraron los conjuntos de cifrado en la versión anterior del protocolo: TLS 1.2, es obvio que la indicación del mecanismo de intercambio de claves se "separó" del conjunto de cifrado durante la transición a TLS 1.3. Además, los métodos estáticos de intercambio de claves RSA y DH se eliminaron de la especificación. Incluso la recuperación de la sesión en TLS 1.3 con la ayuda de PSK y los tickets de la sesión anterior se lleva a cabo de acuerdo con el protocolo ECDHE, donde la última efímera E es especialmente importante.Además, en TLS 1.3, no es posible establecer sus propios valores para el mecanismo Diffie-Hellman: solo queda un conjunto predefinido en las especificaciones del protocolo, hay un consenso con respecto a la seguridad de este conjunto.

De particular interés es el hecho de que los mecanismos modernos de encriptación asimétrica funcionan de manera diferente. En ECC (en particular, cuando se usan certificados ECDSA) utilizamos claves de longitud relativamente corta en comparación con RSA para llegar a niveles aceptables de seguridad. Esto le permite usar criptografía asimétrica fuerte y esquemas de intercambio de claves incluso en dispositivos que, al parecer, no deberían tener suficiente potencia para las operaciones necesarias, por ejemplo, tarjetas inteligentes.

En primer lugar, es necesario aclarar qué significa el término "criptosistema híbrido" tal como se aplica a la descripción de TLS 1.3. El criptosistema híbrido utiliza un esquema de cifrado asimétrico (con una clave pública) para establecer un secreto compartido, que luego se utiliza como clave en un algoritmo de cifrado de secuencia o bloque simétrico.

En segundo lugar, existe una infraestructura de claves públicas (PKI) y certificados (CA). Es interesante que en 2004 Martin Hellman mencionó a uno de los "héroes anónimos": Lauren Könfelder, cuya tesis para defender el diploma de bachiller del MIT era la posibilidad de crear una estructura de árbol, lo que hoy conocemos como PKI. Pero volvamos a los certificados.

El hecho de que el servidor realmente posee la clave privada se verifica mediante su firma, que se puede verificar utilizando la clave pública. Y el archivo de certificado en el servidor certifica que una clave pública específica pertenece a un servidor específico. Esto significa que está estableciendo una conexión segura con el interlocutor deseado, y no con un impostor: su banco, no un fraude cibernético.

TLS 1.3 ha mejorado significativamente el esquema de negociación en comparación con las versiones anteriores del protocolo. Ahora, el servidor firma toda la información recibida en el protocolo de enlace cuando se crea dicha firma: cliente hola y su propio servidor, junto con el conjunto de cifrados seleccionados para su uso. Echemos un vistazo a la sección correspondiente de la descripción de interacción de RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

En TLS 1.3, el cliente envía su parte de la clave (junto con los parámetros necesarios) y la lista de firmas disponibles en el primer mensaje (Client Hello). Las claves necesarias en esta etapa son creadas por el cliente sobre la marcha; el usuario ni siquiera lo nota. Luego, el cliente y el servidor intercambian esta información para crear un secreto común: una clave de sesión que se crea (o, más precisamente, se deriva) del par pre-maestro recibido después de que el servidor respondió al cliente con su mensaje (Server Hello).
En el lado "Server Hello", puede ver el registro correspondiente a la transferencia del certificado al cliente (Certificado *), junto con la verificación CertificateVerify *, que confirma que la parte realmente tiene una clave privada relacionada con el registro de clave pública correspondiente, y luego crea un par de claves de sesión (simétrica) en caso de exito. En otras palabras, la parte que solicita los datos (cliente) ha verificado con éxito la autenticidad de la parte que responde (servidor) al cambiar a un secreto compartido.

Las dos operaciones criptográficas principales están protegidas en esta transferencia: crear una firma y verificar la firma. Estas operaciones generalmente se realizan en diferentes extremos de la conexión, ya que la mayoría de las veces los clientes verifican la autenticidad del servidor. La firma es esencialmente una confirmación de la propiedad de la clave privada correspondiente a la clave pública. Es decir, que recibimos datos del firmante y nos aseguramos de que el mensaje no haya cambiado durante la transferencia.

Cuando se utiliza el algoritmo RSA, como demostraremos un poco más adelante en los números, la operación de crear una firma es la más costosa. Dado que firmamos con una clave de 2048 o 3072 bits, dicha operación carga significativamente el servidor, mucho más fuerte que el cliente durante su verificación (firma).

En ECDSA, operamos con teclas relativamente cortas (en el ejemplo de referencia, analizaremos ECDSA usando la curva NIST P-256 (o secp256v1), pero estas teclas están involucradas en operaciones más complejas. Como resultado, usar ECC puede representarse como un RSA "invertido" con puntos de vista de rendimiento: el cliente se carga mucho más duro con la operación de verificación de firma, mientras que el servidor maneja fácilmente la operación de creación de firma, como lo demuestran las mediciones que proporcionamos en la sección de referencia.

Este efecto ayuda a escalar Internet: dado que los clientes modernos son casi tan poderosos como los servidores (si consideramos solo la velocidad del reloj del núcleo del procesador), pueden asumir una operación computacionalmente difícil sin problemas. El servidor, a su vez, puede usar la potencia informática liberada para crear más firmas y, como resultado, establecer más sesiones.

Firma del certificado en Let's Encrypt

Le proporcionaremos a nuestro lector una instrucción simple y comprensible en la que puede crear independientemente un servidor capaz de establecer una sesión TLS utilizando un par de claves ECDSA en el que Let's Encrypt se firma públicamente y se incluye en el certificado de la cadena de confianza como un certificado.
Decidimos mostrar la ruta completa desde la creación de claves, creando una solicitud de firma de certificado (CSR) para Let's Encrypt y enviándola para su firma utilizando la utilidad certbot, que devuelve las cadenas necesarias y el certificado ECDSA.

Primero necesitas crear un par de claves. Para esto usaremos la biblioteca OpenSSL. La Guía del usuario de OpenSSL dice que la creación de claves para algoritmos basados ​​en curvas elípticas ocurre usando un comando especial dedicado a la familia de algoritmos basados ​​en curvas elípticas.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Para verificar que nuestro equipo funcionó correctamente, ejecutamos el comando ec que indica la ruta al archivo recién creado que contiene la clave privada.

 openssl ec -in privatekey.pem -noout -text 

La salida debería mostrarnos la curva utilizada, con la que se generó la clave.

El siguiente paso es bastante importante al crear una CSR: para no completar el cuestionario necesario para firmar un certificado cada vez, necesitamos un archivo de configuración. Afortunadamente, casi todo el trabajo para nosotros fue realizado por Mozilla, creando el " Generador de configuración SSL ". En él, puede elegir entre una variedad de opciones para los modos de servidor con los que puede establecer una conexión TLS. La configuración limpia de OpenSSL, por alguna razón que falta en el generador de Mozilla, se ve así:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Nota: no es necesario que tenga un archivo de configuración; si no está allí, se le pedirá que complete todos los campos en la línea de comando. Con el archivo de configuración, la ruta a la que especificamos en el siguiente comando, el proceso se simplifica.

Lo siguiente es la creación de la solicitud de firma de certificado (CSR) en sí. Para esto, tenemos un conveniente equipo de OpenSSL.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

También podemos verificar la corrección de la CSR recién creada.

 openssl req -in csr.pem -noout -text -verify 

Finalmente, llegamos a la etapa final: utilizando el cliente ACME, certbot, transferiremos nuestra solicitud para firmar el certificado de la organización Let's Encrypt.

Certbot no solo lo ayudará a obtener un certificado, sino que también tiene muchas otras excelentes opciones. Agregamos que si es nuevo en la criptografía con una clave pública y realmente no comprende la infraestructura de clave pública que existe en este momento, es mejor usar la opción --dry-run antes de intentar obtener un certificado real para cualquiera de sus dominios.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

En este caso, el cliente certbot verifica que la lista de dominios requeridos solicitados en la línea de comando coincide con la lista en la solicitud de firma de certificado (CSR). Dentro de la --dns-somednsprovider poco, ya que hay muchas maneras de confirmar Let's Encrypt que posee una cierta porción del tráfico de Internet. Pero si usa algún tipo de proveedor en la nube, como DigitalOcean, AWS, Azure, Hetzner, lo que sea, es posible que ya tenga una manera más fácil de proporcionar la información que necesita para la certificación, porque su proveedor se ha encargado de la herramienta de integración.

Después de eso, si está seguro de que los parámetros pasados ​​al CSR usando el certbot para Let's Encrypt son correctos, simplemente elimine el parámetro --dry-run del comando y continúe.

Si tiene éxito, el cliente le devolverá varios certificados: el certificado firmado en sí, los certificados intermedio y raíz, así como una combinación de estos últimos en forma de una cadena de certificados, todo en formato .pem.

OpenSSL tiene un comando que usamos para mirar dentro del certificado:

 openssl x509 -in chainfilepath.pem -noout -text 

Ahora debería quedar claro que Let's Encrypt firmó el certificado utilizando el algoritmo hash SHA256. Además de esto, Let's Encrypt solo planea agregar firmas raíz e intermedias a ECDSA, por lo que por ahora sigue siendo contenido con firmas RSA intermedias. Pero no da miedo, porque en cualquier caso usará la clave pública ECDSA.

Al final de esta sección, nos gustaría agregar información sobre la comparación de las longitudes de clave de varios algoritmos. En seguridad de la información, se acostumbra decir que el nivel de seguridad es 2 ^ x, donde x es la longitud del bit (RSA es una excepción, ya que crece algo más lento que el exponente). Para aproximar cómo se comparan las claves de varios algoritmos, nos referimos a la página wiki de OpenSSL :

Como puede ver, las diferencias son notables. Aunque por ahora, Let's Encrypt le permite recibir certificados firmados solo en las claves de solo dos curvas elípticas: 256 (secp256v1) y 384 (secp384r1).

Dificultades conocidas, así como la NSA

Publicado por: xkcd

Quizás el problema central en el uso de la criptografía basada en curvas elípticas fue la necesidad de un generador de números aleatorios muy bien implementado, que se requiere para crear claves de cierto nivel de seguridad.

Un gran escándalo se asoció con el algoritmo Dual_EC_DRBG : tomó muchos años resolverlo. Existe incertidumbre acerca de la base de patentes en torno a ECC; se sabe que muchas patentes pertenecían a Certicom, que fue adquirida por Blackberry. También hay varios casos conocidos de certificación Blackberry ECC. Finalmente, existe una cierta desconfianza en los estándares del NIST, que podrían estar influenciados por la NSA o cualquier otra agencia de inteligencia de los Estados Unidos.

Los errores en la implementación de estándares criptográficos es un tema completamente ortogonal. En 2010, la PlayStation 3 sufrió una fuga de la clave privada de Sony debido a la implementación incorrecta del algoritmo ECDSA: Sony no pudo hacer frente al RNG y proporcionó el mismo número aleatorio, lo que permitió resolver la función con una entrada secreta. OpenSSL sufrió el año siguiente, sin embargo, rápidamente corrigió una vulnerabilidad que le permitió obtener una clave privada mediante un ataque de tiempo; se pueden encontrar más detalles en la publicación de investigación original .

En una conferencia de RSA en 2013, un grupo de investigadores presentó un trabajo de investigación titulado “ ¡Falló al azar! ”Dedicado a las vulnerabilidades de la clase Java SecureRandom. Seis meses después, las cosas comenzaron con las billeteras Bitcoin creadas con un generador de números pseudoaleatorios criptográficamente inseguros.

Debido al hecho de que se descubrieron varias vulnerabilidades graves en un corto período de tiempo, en el mismo agosto de 2013, el IETF lanzó RFC 6979 , que describe la generación determinista de k al crear una clave. Podríamos escribir que el problema se resolvió de esta manera, pero no lo haremos; en cualquier momento, los investigadores pueden encontrar nuevos errores en la implementación debido a desviaciones innecesarias de las especificaciones del protocolo.

Y algunas palabras sobre la NSA. Si no ha estado al tanto del historial de Dual_EC_DRBG, tómese un tiempo y lea los materiales relevantes, no se arrepentirá de haber descubierto los detalles. Edward Snowden se convirtió en parte de esta historia, porque fue debido a sus filtraciones en 2013 que se confirmaron todas las dudas que existían. Esto resultó en el hecho de que muchos criptógrafos eminentes perdieron la confianza en NIST, ya que fue esta organización la que creó y describió muchas de las curvas y algoritmos elípticos que funcionan en ECDSA.

La curva 25519 creada por Daniel Burnshite y la función Diffie-Hellman para la distribución de teclas es la respuesta a muchas de las preguntas anteriores. Y, como ya escribimos, hay un movimiento constante hacia EdDSA. En el caso de las curvas NIST, todavía no se ha encontrado confirmación de su vulnerabilidad, y en cuanto a la experiencia con números aleatorios, fue bastante doloroso y contribuyó a la rápida asimilación.

Para concluir esta parte, nos gustaría citar a John von Neumann: "Cualquiera que tenga debilidad por los métodos aritméticos para obtener números aleatorios está libre de pecado sin ninguna duda".

Algunos puntos de referencia

Utilizamos el servidor NGINX 1.16.0 con la biblioteca OpenSSL versión 1.1.1d para realizar pruebas con dos certificados. Como se mencionó anteriormente, en este momento, Let's Encrypt le permite usar solo los algoritmos prime256v1 y secp384r1 para crear una solicitud de firma de certificado, así como no proporcionar certificados raíz e intermedios con una firma ECDSA, probablemente tratando con esta característica mientras lee esta nota.

Como puede ver, en un solo núcleo de la CPU Intel® Xeon® Silver 4114 a 2.20GHz (lanzado en el tercer trimestre de 17), la diferencia total entre el rendimiento de ECDSA y el RSA generalmente aceptado con una longitud de clave de 2048 bits es 3.5 veces.

Veamos los resultados de ejecutar el comando openssl -speed para ECDSA y RSA en el mismo procesador.

Aquí podemos encontrar la confirmación de una tesis escrita previamente sobre cómo las operaciones computacionales de una firma y su verificación difieren entre ECC y RSA. Actualmente, armado con TLS 1.3, la criptografía basada en curvas elípticas proporciona un aumento significativo en el rendimiento del servidor con un mayor nivel de protección en comparación con RSA. Esta es la razón principal por la cual nosotros en Qrator Labs recomendamos y alentamos a los clientes que también están listos para usar certificados ECDSA. En las CPU modernas, la ganancia de rendimiento a favor de ECDSA es 5x.

Si está interesado en cómo su procesador (hogar o servidor) maneja la computación criptográfica, ejecute el comando de velocidad openssl. Las -rsa , -ecdsa y -eddsa permiten especificar los algoritmos de interés para la evaluación comparativa.

El futuro (en superposición)

Irónicamente, en el proceso de escribir este material, Google anunció "lograr la superioridad cuántica" . ¿Significa esto que ya estamos en peligro y que todo el progreso realizado hasta el momento actual ya no puede garantizar el secreto?

No

Como Bruce Schneier escribió en el ensayo "Criptografía después del aterrizaje alienígena" para la Circular de seguridad y privacidad de IEEE, una computadora cuántica realmente puede infligir un golpe serio solo en la criptografía asimétrica con una clave pública. Los algoritmos simétricos seguirán siendo persistentes.

Pero para continuar, cederemos la palabra al propio Sr. Schneier:

Hay otro escenario futuro que no requiere una computadora cuántica. Si bien ahora tenemos varias teorías matemáticas que subyacen a la unilateralidad utilizada en la criptografía, la prueba de la validez de estas teorías es en realidad uno de los mayores problemas abiertos en informática. Del mismo modo que un criptógrafo inteligente puede encontrar un nuevo truco que facilite la piratería de un algoritmo particular, podemos imaginar extraterrestres con suficiente teoría matemática para descifrar todos los algoritmos de cifrado. Hoy parece ridículo. La criptografía de clave pública es una teoría numérica y es potencialmente vulnerable a los extraterrestres con mentalidad matemática. La criptografía simétrica es tan no lineal, tan simple de crear y complicar, y también lo fácil que es alargar las claves, qué futuro es inimaginable. Un ejemplo es la variante AES con un bloque de 512 bits y un tamaño de clave, así como 128 rondas. Si las matemáticas no son fundamentalmente diferentes de nuestra comprensión actual de las mismas, entonces dicho algoritmo estará seguro hasta que las computadoras estén hechas de algo diferente a la materia y ocupen algo que no sea el espacio.

Pero si sucede lo inimaginable, nos dejará solo con criptografía basada únicamente en la teoría de la información: cuadernos de cifrado desechables y sus variantes.

Bruce Schneier describe perfectamente el área donde, además de los errores de implementación, se pueden encontrar las principales vulnerabilidades de la criptografía moderna. Si en algún lugar hay un grupo de matemáticos, criptoanalistas y criptógrafos acomodados, junto con ingenieros informáticos que trabajan en la prueba o refutación de algunos problemas matemáticos particularmente complejos (como P? = NP), que han logrado lograr cierto progreso en esta actividad en este momento: Nuestra posición es vulnerable. Al rechazar las teorías de conspiración, se puede decir que dicho progreso en los campos de la informática, la teoría de la información y la teoría de la computabilidad difícilmente se puede ocultar. Tal evento escribiría los nombres de sus propios creadores en las páginas de Historia y, en particular, en los libros de texto de Historia de Internet, lo cual es invaluable para cualquier individuo o grupo tan intelectual. Por lo tanto, un escenario similar puede descartarse como imposible.

Tampoco está claro si tales éxitos en la computación cuántica se lograrán en los próximos 5 años, y después de todo, ya hay primitivas criptográficas adecuadas para su uso en el mundo post-cuántico: redes, usando isogenización supersingular de curvas elípticas, funciones hash, códigos de corrección de errores. Ahora, los expertos en seguridad solo están experimentando con ellos, pero no hay duda de que, si es necesario, la humanidad encontrará la manera de implementar rápidamente nuevos algoritmos a cualquier escala.

Solo resta agregar que para la próxima década, la criptografía basada en curvas elípticas parece ser ideal para los objetivos y necesidades que la mayoría de sus usuarios se establecen, brindando seguridad y alto rendimiento.