Al girar, reorganizar y bajar una secuencia predeterminada de formas, el algoritmo de impresora Tetris utiliza la mecánica de Tetris para generar mapas de bits arbitrarios.
Descripción del algoritmo
El algoritmo convierte los píxeles de la imagen de origen en los cuadrados del campo
Tetris línea por línea, moviéndose de abajo hacia arriba. Para generar un solo cuadrado, el algoritmo ensambla una estructura que consiste en un área rectangular que está completamente soportada por un cuadrado debajo de él. Después de completar el ensamblaje de la región rectangular, sus líneas se borran, dejando un cuadrado debajo de ella. Aquí hay tres ejemplos de este comportamiento.
Como se muestra a continuación, el algoritmo también puede generar varios cuadrados con una estructura.
En el proceso de construcción de una fila, todos los cuadrados creados de esta manera deben basarse en algo. En las imágenes mostradas arriba, los cuadrados generados están en el piso del campo de juego. Sin embargo, si una línea arbitraria contiene agujeros, no podrá proporcionar el soporte necesario para construir una línea sobre ella. El algoritmo resuelve este problema creando una plataforma plana en la parte superior de la cadena con agujeros. En la animación a continuación, una plataforma construida en la parte superior de una línea consta de un cuadrado rojo. Una plataforma es una estructura temporal, y al insertar la última forma se elimina.

La fila de 5 cuadrados rojos que se muestra a continuación está en la parte superior de la fila de 3 cuadrados rojos. Esto se logra mediante la construcción de una plataforma plana en la parte superior de la línea de fondo. La plataforma proporciona el soporte necesario para generar 5 cuadrados rojos. Al final, la plataforma se elimina insertando la última forma, y la nueva línea cae en su lugar. Tenga en cuenta que si el algoritmo necesita generar líneas en el orden inverso (una línea de 3 cuadrados rojos sobre una línea de 5 cuadrados rojos), entonces la plataforma no será necesaria.
Patrones de una plaza
Como referencia, daré los nombres de 7 tetramino (piezas del juego).
La versión del algoritmo de impresora Tetris presentada en el artículo está diseñada específicamente para renderizar sprites de videojuegos antiguos. Estos juegos empacaron gráficos en 8 × 8 mosaicos, y se asignaron 2 bytes por cada píxel. Por lo tanto, los sprites generalmente contenían solo 3 colores más áreas transparentes y con mayor frecuencia tenían un tamaño de 16 × 16 o 16 × 32 píxeles.
La animación a continuación muestra todos los patrones utilizados para crear cuadrados individuales. Cada patrón utiliza tetramino intercambiable J, T y L, creando un único cuadrado en la parte inferior. El algoritmo asigna este tetramino a uno de los 3 colores presentes en el sprite. Al resto del tetramino se le asignan colores arbitrarios. A lo largo del juego, todos los colores permanecen constantes.
Debido a la forma de los tres tetramino, es imposible crear un cuadrado a partir de los tres colores en las primeras dos y últimas dos columnas. Por lo tanto, el ancho mínimo del campo de juego para renderizar un sprite con un ancho de 16 píxeles es 2 + 16 + 2 = 20 cuadrados. Sin embargo, resultó que 20 es muy poco.
Como se muestra a continuación, el área sobre el cuadrado inferior único no puede consistir en una sola línea, porque las únicas figuras que pueden caber en ella (tetramino I) no tienen soporte.
Con dos líneas, la única forma de estirar todo el campo de juego para que tenga soporte es usar tetramino S y Z. Pero en este caso, los agujeros permanecerán en la línea superior.
El número mínimo de líneas requeridas sobre el cuadrado inferior es 3, y como se muestra varias veces arriba, tales patrones existen. 20 cuadrados es el ancho mínimo requerido para colocar un sprite con un ancho de 16 píxeles. Pero 20 × 3 + 1 = 61, y este número no es divisible por 4, lo que significa que no se puede construir a partir de tetramino. Sin embargo, un ancho de 21 nos da 21 × 3 + 1 = 64, y se puede construir a partir de 16 tetramino. De hecho, este ancho permite que el algoritmo renderice sprites de hasta 17 píxeles de ancho.
El campo de juego del Tetris original tiene un tamaño de 10 × 20 cuadrados (relación 1: 2). En esta versión del algoritmo, esta relación se conserva: el campo de juego tiene un tamaño de 21 × 42 cuadrados.
Dado que el tetramino J, T y L son intercambiables cuando se crea un cuadrado, y 3 cuadrados de estos tetramino están involucrados en la creación de una línea por encima de él, hay 21 - 3 = 18 patrones para crear un solo cuadrado. Sin embargo, debido a la simetría de espejo, en realidad solo hay 9. Hay 3 líneas que funcionan para la mayoría de estos 9. Sin embargo, un estudio exhaustivo por computadora mostró que los dos patrones necesitaban más. La siguiente opción posible es 7 líneas, porque 21 × 7 + 1 = 148, que requiere 37 tetraminos. Como se muestra en las imágenes a continuación, existen tales patrones.
Múltiples patrones cuadrados
Los patrones para crear múltiples cuadrados están limitados a los mismos tres colores creados por los patrones de un solo cuadrado. Los cuadrados resultantes se crean a partir de tetramino J, T y L, cada uno de los cuales ocupa 3 cuadrados en una línea sobre la línea de creación. El número máximo de cuadrados que se pueden crear potencialmente con un solo patrón es 21/3 = 7. Sin embargo, para sprites con un ancho de 16 píxeles, el tetramino más a la derecha no puede crear un cuadrado. Incluso en el caso de sprites con un ancho de 17 píxeles, puede crear un cuadrado de un solo color. Por lo tanto, el patrón de crear a partir de 7 cuadrados rara vez se usa.

El número de patrones para crear un número arbitrario de cuadrados se puede determinar utilizando la combinatoria de enumeraciones. Considere el siguiente patrón, que representa una fila sobre una fila de tres cuadrados. Cada bloque de tres cuadrados blancos adyacentes designa una parte de tetramino; los cuadrados creados no se muestran.
Tres tetramino crean 4 vacíos. Hay 21 - 3 × 3 = 12 cuadrados oscuros que se pueden insertar arbitrariamente en estos vacíos para formar un patrón específico. El número de formas de distribuir estos cuadrados oscuros se puede calcular colocándolos en una línea en la que los cuadrados blancos individuales se tratan como divisores.
Entonces, la tarea se redujo a calcular el valor del coeficiente del polinomio. Si observa estos cuadrados blancos, puede comprender que se trata de la cantidad de formas de elegir 3 de 15.
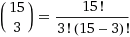
= 455.
En el caso general, para
n es igual a
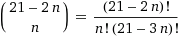
. Pero debido a la simetría del espejo, de hecho, son la mitad; si la cantidad es impar, luego dividiendo por dos, redondeamos al entero más cercano para incluir en él un patrón perfectamente simétrico que debería existir en este conjunto, como, por ejemplo, se muestra a continuación para el caso con 455.
Aplicando esta fórmula a 7 tetramino, confirmamos lo obvio: solo hay un patrón para crear 7 cuadrados.
El patrón de crear 6 cuadrados se puede construir de dos maneras: dos líneas rellenas (2 × 21 + 6 = 48) y seis líneas rellenas (6 × 21 + 6 = 132), lo que requiere 12 y 33 tetramino. La fórmula anterior muestra que hay 84 patrones para crear 6 cuadrados, pero solo 35 de ellos se pueden construir a partir de 2 líneas completas. 49 patrones requieren 6 líneas. Los números son impares debido a los patrones simétricos que se muestran a continuación.
También vale la pena señalar que aquí son posibles 2 líneas, porque en contraste con el patrón de crear un cuadrado que requería tetramino S y Z, se usan 6 figuras en estos patrones.
La tabla a continuación muestra el número de cuadrados creados por cada tipo de patrón, el número de líneas completas, el número de tetramino utilizado y el número de patrones.
Ejemplos de patrones.
Plataformas
Antes de construir una línea, el algoritmo examina la línea debajo de ella. Si la fila inferior no puede proporcionar soporte para todos los cuadrados encima de ella, entonces se necesita una plataforma temporal. Cuando se retira la plataforma, baja una nueva línea y, debido a cómo se implementa la gravedad en el Tetris original, algunos cuadrados permanecen suspendidos en el aire.
La siguiente ilustración muestra 10 patrones de plataforma. La construcción de la plataforma comienza bajando el tetramino T en la parte superior de uno de los cuadrados de la última línea generada. Los tetraminos restantes se basan en esta primera T. Es decir, si la línea generada anterior contiene al menos 1 cuadrado, como el cuadrado rojo en la imagen a continuación, podemos crear una plataforma plana encima para generar la siguiente línea.

En el medio de la construcción de la plataforma, la línea de fondo se completa y se elimina, dejando tres líneas sobre ella. El último tetramino J o L, que eliminará estas líneas, no se inserta hasta que los patrones de creación generen la siguiente línea de sprite en la parte superior de la plataforma. Esta última figura impide la creación de cuadrados en las dos primeras y últimas líneas. Pero, como se mencionó anteriormente, debido a la geometría del tetramino J, T y L utilizados en este proceso, los patrones para crear cuadrados están limitados a 17 columnas internas.
Además, de las 19 formas posibles de construir plataformas sobre Tetramino T, solo se muestran 10 arriba.
Matrices Empaquetadas
Como se indicó anteriormente, un subconjunto de los patrones de creación de 6 cuadrados implica borrar solo dos líneas. Todos los demás patrones requieren 6 líneas. Para entender por qué este es el caso, considere el siguiente patrón.
Estos tetramino son intercambiables con tetramino J y L, y cada uno de ellos agrega 3 cuadrados adyacentes a la fila común. Las filas a completar están representadas por la matriz que se muestra a continuación.
Ahora todo está empacando el espacio vacío con tetramino. Comenzando por la izquierda, la única opción es usar la secuencia de tetramino I.
La única forma de llenar el espacio restante es usar J y O o I y L. Ambas opciones se muestran a continuación.
Desafortunadamente, el tetramino O y L no son compatibles con las matrices que se muestran arriba. Este patrón de 6 cuadrados requiere una matriz más grande.
Un problema similar surge en dos patrones de crear un cuadrado. Considere la matriz a continuación:
La única forma de llenar la línea inferior a la derecha es encadenar la secuencia Z.
Del mismo modo, la única forma de obtener 3 cuadrados vacíos en la esquina inferior izquierda es tetramino S.
En la línea media hay un cuadrado vacío entre S y Z y la única forma de llenarlo es usando tetramino J, T o L, como se muestra en las siguientes figuras.
Insertar cualquiera de estas formas divide el espacio en blanco. El área vacía a la izquierda contiene 5, 6 y 7 huecos, respectivamente. Como ninguno de estos valores es divisible por 4, es imposible continuar. Se requiere una matriz más grande para este patrón cuadrado único.
Lo mismo se aplica a otro patrón para crear un cuadrado, que se muestra en la matriz a continuación.
Después de usar tetramino S y Z para llenar la mayor parte de la línea inferior, hay un espacio vacío entre ellos en la línea media.
Como se muestra en las imágenes a continuación, el inserto del agujero divide el espacio vacío, y el área vacía de la izquierda contiene 9, 10 u 11 cuadrados, respectivamente; ninguno de los números es divisible por 4.
Pero empacar matrices no es la única forma de generar un patrón de cuadrados. Por ejemplo, eche un vistazo al creador de 4 cuadrados a continuación.
El siguiente es un intento de representar el patrón como un conjunto de tetraminos empaquetados.
La última L se omite, porque el espacio para ella se forma solo después de completar y eliminar la tercera fila.
Pero después de una búsqueda exhaustiva, se descubrió que esta técnica no proporciona los patrones de un cuadrado antes mencionados con la capacidad de trabajar con solo 3 líneas. Además, no le permite implementar ningún patrón nuevo de 6 cuadrados en dos líneas. No es necesario buscar los patrones restantes fuera de las matrices empaquetadas, porque ya usan la menor cantidad posible de tetramino. Y limitándonos a las matrices empaquetadas, encontraremos todos los patrones necesarios mucho más rápido.
Búsqueda de patrones
Para simplificar la salida de datos, el algoritmo de impresora Tetris se limita a crear tetramino en el punto central superior del campo de juego, girarlo, moverlo horizontalmente y bajarlo. Nunca tiene que mover la figura horizontalmente después de pasar cierta distancia. Esta restricción reduce en gran medida el espacio de búsqueda, ya que no permite la formación de espacios debajo de las cifras agregadas a la matriz. Como ejemplo, veamos la siguiente matriz de 3 cuadrados.
Si arrojamos J en el centro de la matriz, como se muestra arriba, obtenemos un espacio de 2 cuadrados vacíos, que no se pueden llenar con las figuras posteriores. Por lo tanto, la búsqueda no seguirá este camino.
Como los espacios cubiertos no están permitidos, cada columna de la matriz se puede considerar como una pila de cuadrados rellenos y la altura de estas pilas describe completamente el contenido de toda la matriz. Independientemente del número de filas, una matriz entera unidimensional con 21 elementos será suficiente para describir una matriz bidimensional.
Cuando una figura cae en la matriz, las alturas de las pilas de las columnas correspondientes aumentan. Para acelerar este proceso, todas las tetraminas se analizan por adelantado. Hay 19 giros de tetramino, y la búsqueda considera que cada uno de ellos es una figura única.
El tetramino J en la esquina superior izquierda de la imagen ocupa 3 columnas. Al bajar a la matriz, las alturas de 3 pilas adyacentes aumentan en 1, 1 y 2 casillas, respectivamente. Pero antes de que se pueda bajar la figura, el perfil inferior de la figura debe corresponder al perfil superior de las pilas respectivas. Si este J estuviera en el piso del campo de juego, debajo de cada una de estas columnas debería haber espacios de 1, 1 y 0 cuadrados vacíos. Dado que los espacios libres están prohibidos, las alturas relativas de 3 pilas tendrán que coincidir completamente con el patrón.
Otra consecuencia de la falta de espacios fue que cuando las figuras caen en la matriz, las filas se llenan de abajo hacia arriba. No es posible llenar una fila en el medio de una matriz antes o simultáneamente no completar todas las filas debajo de ella. En el proceso de llenar la matriz, su límite inferior se mueve realmente hacia arriba. Por lo tanto, una pila de columnas de matriz puede proporcionar soporte solo si su altura menos el número de filas completadas es mayor que 0. Cuando se agrega una forma a la matriz, al menos una de las columnas correspondientes debe proporcionar soporte.
La búsqueda almacena una segunda matriz unidimensional que contiene el número de cuadrados rellenos en cada fila. La J anterior contiene en las líneas correspondientes 3 y 1 un cuadrado. Cuando lo inserta en la matriz, estos valores se agregan a los elementos correspondientes de la matriz. El número de líneas completadas es el número de elementos con un valor de 21.
Como se indicó en la sección anterior, si la figura agregada divide la matriz, entonces los tamaños de las áreas resultantes deben dividirse entre 4. Por ejemplo, en la imagen a continuación, al agregar I crea 2 áreas, cada una de las cuales contiene 46 cuadrados vacíos. Dado que 46 no es divisible por 4, ya no hay forma de completar el resto de la matriz.
La separación aparece cuando la altura de la pila es igual a la altura de la matriz. Después de insertar la figura incrementando las alturas de las pilas respectivas, las dimensiones de todas las áreas divididas de espacio vacío se pueden determinar escaneando la matriz de alturas y sumando el espacio restante en cada pila. Este número se verifica y restablece cuando se detecta una división.
La búsqueda utilizada para generar todos los patrones utiliza una construcción incremental aleatoria, un algoritmo de retroceso que verifica sistemáticamente todas las combinaciones en orden aleatorio. La construcción incremental de una solución al insertar formas al azar hace que crezca como un cristal. La aleatoriedad proporciona una irregularidad que contiene caras rotas que sirven de base para las formas agregadas posteriores. La mayor parte de la matriz se empaqueta aleatoriamente muy rápidamente, y cuando el espacio vacío se vuelve escaso, el retroceso entra en juego.
Antes de realizar la búsqueda, se realizan permutaciones aleatorias de 371 formas de agregar una figura a la matriz. El pseudocódigo de la función de búsqueda se muestra a continuación.
private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if ( S Z) { S Z if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } for( , ) { if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION }
La matriz original pasada a la función de búsqueda está vacía, excepto por la fila inferior que contiene bloques de 3 cuadrados adyacentes. Se transmite junto con el número de cifras restantes que deben agregarse. Si el
remaining es 0, la matriz contiene la solución y la función vuelve. Cada llamada recursiva incrementa el número global de intentos de
attempts . Si supera
MAX_ATTEMPTS , que tiene un valor de 1000, la búsqueda comienza nuevamente.
La tercera
if intenta agregar tetramino S o Z al fondo de la matriz si el espacio lo permite. El significado de esto es evitar situaciones como la que se muestra a continuación, cuando el algoritmo pasa tiempo llenando parte de la matriz, no pudiendo llenar el resto debido a la falta de soporte.
Gracias a la
if forma rápidamente una plataforma sobre la cual construir:
Para intentar agregar una figura a la matriz, se requieren las verificaciones anteriores. El algoritmo verifica si la figura tendrá soporte, dadas las líneas completadas. También comprueba si divide entre 4 el tamaño de cada espacio vacío individual creado por la inserción de la forma.
Conversión de imagen
El algoritmo de impresora Tetris convierte cada línea del mapa de bits en una serie de pasadas. Moviéndose de izquierda a derecha, cada pasaje de una manera "codiciosa" inserta tetramino J, T y L donde se colocan. Por ejemplo, la imagen a continuación muestra una fila de 16 píxeles de un mapa de bits.
La imagen a continuación muestra los 5 pases necesarios para cubrir estos 16 píxeles.
La secuencia de formas que el algoritmo intenta insertar está determinada por los colores de los píxeles. Para que las formas no se superpongan, se utiliza una matriz unidimensional de valores booleanos. Para insertar una figura, deben estar presentes 3 elementos cero en la matriz. Tras la inserción exitosa de la figura 3, los elementos de la matriz correspondientes toman el valor 1.
Para rastrear píxeles completados entre múltiples pasadas, se utiliza una segunda matriz unidimensional de valores booleanos. Cuando cada elemento es 1, la línea está completa.
Al final de cada pasada, el convertidor de imágenes busca en la tabla todos los patrones para crear uno o más cuadrados. A la salida, pasa el patrón correspondiente con el tetramino J, T y L insertados en la parte inferior. Por ejemplo, el primer paso que se muestra arriba se muestra como el siguiente patrón de creación de 5 cuadrados:
Búsqueda en tiempo real
El convertidor de imágenes descrito en la sección anterior es extremadamente rápido porque utiliza una tabla constante que contiene todos los patrones para crear cuadrados y no los busca en tiempo real. Sin embargo, la búsqueda en tiempo real puede usar patrones que no están en la tabla y, por lo tanto, reducir en gran medida la cantidad de tetramino necesaria para generar la imagen. Utiliza los cuadrados creados en pasajes anteriores, utilizándolos como soportes adicionales. Por ejemplo, como se mencionó anteriormente, el siguiente patrón para crear un cuadrado requiere 7 líneas completas.
Pero un cuadrado rojo creado en el pasaje anterior en la esquina inferior izquierda de la imagen a continuación proporciona soporte adicional, reduciendo el número de líneas rellenas a 3.
Además, una búsqueda en tiempo real puede cubrir 3 píxeles adyacentes del mismo color volteando tetramino J, T o L.
De hecho, puede combinar tetramino invertido e invertido, cubriendo una gran cantidad de píxeles en una pasada. Por ejemplo, los 5 pases anteriores necesarios para cubrir 16 píxeles se pueden reducir al pase único que se muestra a continuación.
Para obtener este patrón, el convertidor de imágenes comienza empacando ansiosamente tetramino J, T y L.
Luego, intenta con entusiasmo agregar las versiones sin girar, y en este caso se las arregla para agregar otra J.
En principio, una tabla de búsqueda precalculada también se puede utilizar en este proceso, pero el gran tamaño de dicha tabla la hace inaplicable en la práctica.
En este ejemplo, se agregan 8 cuadrados en una fila sobre la fila que se creará a la fila inferior de la matriz vacía. Para
n cuadrados en un campo de juego de 21 cuadrados de ancho, la altura de la matriz
h es el número entero positivo más pequeño, de modo que
21h - n es divisible por 4. En este caso, se requiere una matriz de altura 4.
La búsqueda en tiempo real funciona exactamente de la misma manera que el algoritmo de búsqueda descrito anteriormente, pero tiene mejoras menores. Como antes, la pila de columnas de la matriz proporciona soporte solo si la altura de la columna menos el número de filas completadas es mayor que cero. Cuando la diferencia es cero, la pila de columnas no debe proporcionar soporte. Sin embargo, en esta versión, si es igual a cero, verifica los cuadrados en la línea creada generada por los pases anteriores. Es decir, cualquier cuadrado en la fila debajo de la fila inferior de la matriz proporciona soporte para columnas vacías.
Además, dado que la búsqueda se realiza en tiempo real, no será práctico hacerla exhaustiva. Si no encuentra una solución después de un número determinado de intentos, agrega 4 filas más en la parte superior de la matriz y luego lo intenta nuevamente. Después de eso, si aún no pudo encontrar una solución después de un número dado de intentos, en el pasaje actual regresa al método con tablas de búsqueda precalculadas y conversión de imágenes descritas en la sección anterior del artículo.
Imprimir
Para imprimir, debe seguir las instrucciones que muestra el convertidor de imágenes en el campo de juego de Tetris. La impresora crea un tetramino específico en el punto central superior del campo de juego en una orientación estándar. Luego la impresora lo gira, lo mueve horizontalmente y lo baja. Este proceso se muestra en el video:
Código fuente
El código fuente para el proyecto Java 7 está disponible
aquí .
Los algoritmos de búsqueda para tablas preparadas y en tiempo real se encuentran en los paquetes
search.precomputed y
search.realtime . Utilizan algunas clases comunes ubicadas en el paquete de
search . Los resultados de una búsqueda calculada previamente se almacenan en el paquete de
patterns como una secuencia de archivos de texto. Los archivos de texto almacenan matrices empaquetadas como caracteres ASCII, comenzando con
A Por ejemplo, las primeras 3 matrices en
emitters1.txt (el conjunto de patrones para crear un cuadrado) se ven así:
Como se indica repetidamente en el artículo, 3 símbolos
A adyacentes en las matrices anteriores se pueden reemplazar con tetramino J, T o L. Los símbolos
B ,
C ,
D y así sucesivamente representan la secuencia de tetramino que necesita crear.
La clase
imageconverter.ImageConverter contiene el método
main , que recibe un único argumento de línea de comando: el nombre del archivo sprite de imagen. Una imagen no puede tener más de 17 × 32 píxeles y no puede contener más de 3 colores opacos. Todos los demás píxeles deben ser transparentes.
Curiosamente, en los videojuegos antiguos, los desarrolladores a menudo usaban el fondo para obtener más color. Por ejemplo, alumnos y boca de Bubble from Bubble bobble, alumnos de Donkey Kong de Donkey Kong y cejas con el lunar de Miss Pakman de Ms. Pac-Man es en realidad transparente. El negro se obtiene de un fondo sólido.
El fondo del campo de juego de Tetris se puede utilizar de manera similar.
ImageConverter resultado de
ImageConverter se parece a este fragmento:
Los 3 valores hexadecimales en la primera línea son 3 colores opacos extraídos del archivo de imagen de sprite. Corresponden a los colores de tetramino J, T y L. Los colores de otros tetramino no afectan la imagen. Los bloques restantes son patrones empaquetados ejecutados en el campo de juego (para los caracteres después de
Z y hasta a
a vea la
tabla de caracteres ASCII ). Los bloques amarillos resaltados forman la plataforma. El primer bloque agrega la plataforma, el segundo la elimina.
La clase
printer.Printer recibe un archivo de texto en este formato y genera un archivo de imagen al jugar Tetris.
El algoritmo de la impresora utilizado para generar un video parecido a la
versión NES de Tetris define cada tipo de tetramino en cada bloque de un archivo de texto. Luego se mueve en el orden opuesto desde el punto de partida y la orientación inicial hacia el ángulo de rotación y las coordenadas de la reducción de la figura indicada en el archivo. Nota: debido a la velocidad extremadamente alta de las figuras que caen, es imposible ir más allá del nivel 30 en la versión NES real de Tetris. Se supone que la impresora transmite todos sus comandos al campo de juego lo suficientemente rápido. para compensar esto.
Para regenerar archivos de patrones, use
search.precomputed.PatternSearcher . Se puede personalizar cambiando las constantes al comienzo del archivo de código fuente.
public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000;
RANDOM_SETS es el número de permutaciones aleatorias de 371 formas de agregar una figura a la matriz. Cuando se establece en
100000 , lleva varios segundos inicializar las permutaciones al inicio. Además, su almacenamiento requiere más de un gigabyte de memoria.
MAX_ATTEMPTS controla el tiempo de ejecución de una búsqueda. Un valor relativamente pequeño de
1000 permite que la búsqueda descarte rápidamente los comienzos aleatorios que no se muestran bien. Sin embargo, para demostrar que para un tamaño de matriz específico y el número de cuadrados creados no hay solución, es necesario explorar completamente todo el espacio de búsqueda. Para hacer esto, puede establecer
MAX_ATTEMPTS en
Integer.MAX_VALUE .
Constantes similares se encuentran en
search.realtime.RealtimeSearcher , que utiliza el convertidor de imágenes. Como se mencionó anteriormente, un valor
RANDOM_SETS grande requiere un aumento en la memoria máxima y conduce a un inicio más largo.
MAX_RETRIES controla el número de intentos, después de los cuales la búsqueda en tiempo real se rinde y vuelve a la búsqueda con una tabla calculada previamente.
Tenga en cuenta que ambos algoritmos de búsqueda utilizan el 100% de la CPU, creando muchos subprocesos paralelos que tienen el mismo tamaño que la cantidad de procesadores disponibles.