Phoebe Wong, científica y directora financiera de Equal Citizens, habló sobre el conflicto cultural en la ciencia cognitiva. Elena Kuzmina tradujo el artículo al ruso.
Hace unos años vi una discusión sobre el procesamiento del lenguaje natural. Hablaron el "padre de la lingüística moderna"
Noam Chomsky y el nuevo portavoz de la guardia,
Peter Norvig , director de investigación de Google.
Chomsky reflexionó en qué dirección se mueve la esfera del procesamiento del lenguaje natural y
dijo :
Supongamos que alguien está a punto de liquidar un departamento de física y quiere hacerlo según las reglas. De acuerdo con las reglas, esto es tomar una cantidad infinita de videos sobre lo que está sucediendo en el mundo, alimentar estos gigabytes de datos a la computadora más grande y rápida y realizar un análisis estadístico complejo, bueno, entiendes: Bayesiano "de ida y vuelta" * y obtendrás un cierto pronóstico sobre lo que está por suceder fuera de tu ventana. De hecho, obtendrá un pronóstico mejor que el que da la Facultad de Física. Bueno, si el éxito está determinado por lo cerca que esté de la masa de datos brutos caóticos, entonces es mejor hacerlo que la forma en que lo hacen los físicos: no realizar experimentos mentales en superficies ideales, etc. Pero no obtendrá el tipo de comprensión que la ciencia siempre ha buscado. Lo que obtienes es solo una idea aproximada de lo que está sucediendo en la realidad.
* De la probabilidad de Bayes: una interpretación del concepto de probabilidad, en el que, en lugar de la frecuencia o tendencia a algún fenómeno, la probabilidad se interpreta como una expectativa razonable, que representa una evaluación cuantitativa de una creencia personal o estado de conocimiento. Los investigadores de inteligencia artificial utilizan estadísticas bayesianas en el aprendizaje automático para ayudar a las computadoras a reconocer patrones y tomar decisiones basadas en ellos.
Chomsky enfatizó repetidamente esta idea: el éxito actual en el procesamiento del lenguaje natural, es decir, la precisión de los pronósticos, no es una ciencia. Según él, arrojar una gran cantidad de texto en una "máquina compleja" es simplemente aproximarse a datos sin procesar o recolectar insectos, no conducirá a una comprensión real del idioma.
Según Chomsky, el objetivo principal de la ciencia es descubrir principios explicativos de cómo funciona realmente el sistema, y el enfoque correcto para lograr este objetivo es permitir que la teoría dirija los datos. Es necesario estudiar la naturaleza básica del sistema mediante la abstracción de "inclusiones irrelevantes" con la ayuda de experimentos cuidadosamente diseñados, es decir, de la misma manera que fue aceptado en la ciencia desde la época de Galileo.
En sus palabras:
Es poco probable que un simple intento de lidiar con datos caóticos sin procesar lo lleve a ninguna parte, así como Galileo no lo haría a ninguna parte.
Posteriormente, Norwig respondió a las afirmaciones de Chomsky en un
largo ensayo . Norvig señala que en casi todas las áreas de la aplicación del procesamiento del lenguaje: motores de búsqueda, reconocimiento de voz, traducción automática y respuesta a preguntas, prevalecen los modelos probabilísticos capacitados porque funcionan mucho mejor que las herramientas antiguas basadas en reglas teóricas o lógicas. Él dice que el criterio de éxito de Chomsky en la ciencia, el énfasis en la pregunta "por qué" y la subestimación de la importancia de "cómo", está mal.
Confirmando su posición, cita a Richard Feynman: "La física puede desarrollarse sin evidencia, pero no podemos desarrollar sin hechos". Norwig recuerda que los modelos probabilísticos generan varios billones de dólares al año, mientras que los descendientes de la teoría de Chomsky ganan mucho menos de mil millones, citando los libros de Chomsky vendidos en Amazon.
Norwig sugiere que el desprecio de Chomsky por "Bayesian de ida y vuelta" se debe a la división entre las
dos culturas en el modelo estadístico descrito por Leo Breiman:
- Una cultura de modelado de datos que asume que la naturaleza es un cuadro negro donde las variables están conectadas estocásticamente. El trabajo de los expertos en modelado es determinar el modelo que mejor se adapte a las asociaciones que subyacen.
- La cultura del modelado algorítmico implica que las asociaciones en una caja negra son demasiado complejas para ser descritas usando un modelo simple. El trabajo de los desarrolladores de modelos es seleccionar el algoritmo que mejor evalúa el resultado utilizando variables de entrada, sin esperar que se puedan entender las verdaderas asociaciones básicas de variables dentro del cuadro negro.
Norwig sugiere que Chomsky no es tan polémico con los modelos probabilísticos como tales, sino que no acepta modelos algorítmicos con "miles de millones de parámetros": no son fáciles de interpretar y, por lo tanto, son inútiles para resolver las preguntas de "por qué".
Norwig y Breiman pertenecen a otro campo: creen que los sistemas como los idiomas son demasiado complejos, aleatorios y arbitrarios para ser representados por un pequeño conjunto de parámetros. Y abstraerse de las dificultades es similar a hacer que una herramienta mística esté sintonizada en un área permanente que realmente no existe y, por lo tanto, se pasa por alto la cuestión de qué lenguaje es y cómo funciona.
Norwig reafirma su tesis en
otro artículo , donde argumenta que deberíamos dejar de actuar como si nuestro objetivo fuera crear teorías extremadamente elegantes. En cambio, debe aceptar la complejidad y utilizar nuestro mejor aliado: eficiencia de datos irrazonable. Señala que en el reconocimiento de voz, la traducción automática y casi todas las aplicaciones de aprendizaje automático para datos web, los modelos simples como los modelos de n-gramas o los clasificadores lineales basados en millones de funciones específicas funcionan mejor que los modelos complejos. quienes intentan descubrir las reglas generales.
Lo que más me atrae en esta discusión no es con lo que Chomsky y Norvig no están de acuerdo, sino con lo que están unidos. Están de acuerdo en que analizar grandes cantidades de datos utilizando métodos de aprendizaje estadístico sin comprender las variables proporciona mejores predicciones que un enfoque teórico que intenta modelar cómo las variables se relacionan entre sí.
Y no soy el único que está desconcertado por esto: muchas personas con antecedentes matemáticos con quienes hablé también encuentran esto contradictorio. ¿No debería el enfoque más adecuado para modelar relaciones estructurales básicas también tener el mayor poder predictivo? ¿O cómo podemos predecir algo con precisión sin saber cómo funciona todo?
Predicciones contra la causalidad
Incluso en los campos académicos, como la economía y otras ciencias sociales, los conceptos de poder predictivo y explicativo a menudo se combinan entre sí.
Los modelos que demuestran una alta capacidad de explicación a menudo se consideran altamente predictivos. Pero el enfoque para construir el mejor modelo predictivo es completamente diferente del enfoque para construir el mejor modelo explicativo, y las decisiones de modelación a menudo conducen a compromisos entre los dos objetivos. Las diferencias metodológicas se ilustran en
Introducción al aprendizaje estadístico (ISL).
Modelado predictivo
El principio fundamental de los modelos predictivos es relativamente simple: evalúe Y usando un conjunto de datos de entrada X. Si el error X es en promedio cero, Y puede predecirse usando:
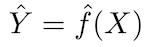
donde ƒ es la información sistemática sobre Y proporcionada por X, que conduce a Ŷ (predicción de Y) para una X dada. La forma funcional exacta generalmente no es significativa si predice Y, y ƒ se considera como un "recuadro negro".
La precisión de este tipo de modelo se puede descomponer en dos partes: un error reducible y un error fatal:
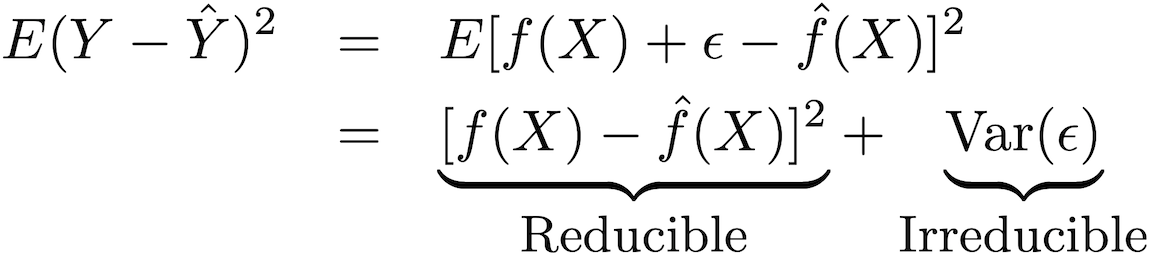
Para aumentar la precisión del pronóstico del modelo, es necesario minimizar el error reducible, utilizando los métodos más adecuados de capacitación estadística para la estimación con el fin de evaluar ƒ.
Modelado de salida
ƒ no puede considerarse como un "recuadro negro" si el objetivo es comprender la relación entre X e Y (cómo cambia Y en función de X). Porque no podemos determinar el efecto de X en Y sin conocer la forma funcional ƒ.
Casi siempre al modelar conclusiones, se utilizan métodos paramétricos para estimar ƒ. El criterio paramétrico se refiere a cómo este enfoque simplifica la estimación de ƒ al tomar la forma paramétrica ƒ y evaluar ƒ a través de los parámetros propuestos. Hay dos pasos principales en este enfoque:
1. Haga una suposición sobre la forma funcional ƒ. La suposición más común es que ƒ es lineal en X:
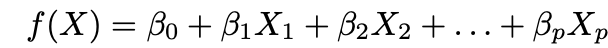
2. Utilice los datos para ajustar el modelo, es decir, encuentre los valores de los parámetros β₀, β₁, ..., βp de manera que:
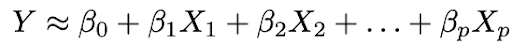
El enfoque de ajuste de modelo más común es el método de mínimos cuadrados (OLS).
El compromiso entre flexibilidad e interpretabilidad
Quizás ya se esté preguntando: ¿cómo sabemos que ƒ es lineal? De hecho, no lo sabremos, ya que la verdadera forma ƒ es desconocida. Y si el modelo seleccionado está demasiado lejos del real ƒ, nuestras estimaciones estarán sesgadas. Entonces, ¿por qué queremos hacer tal suposición en primer lugar? Porque existe un compromiso inherente entre la flexibilidad del modelo y la interpretabilidad.
La flexibilidad se refiere al rango de formas que un modelo puede crear para adaptarse a las diferentes formas funcionales posibles ƒ. Por lo tanto, cuanto más flexible sea el modelo, mejor ajuste puede crear, lo que aumenta la precisión de la predicción. Pero un modelo más flexible es más complejo y requiere más parámetros para ajustarse, y las estimaciones de a menudo se vuelven demasiado complejas para que se interpreten las asociaciones de cualquier predictor individual y factores pronósticos.
Por otro lado, los parámetros en el modelo lineal son relativamente simples e interpretables, incluso si no realiza un pronóstico preciso muy bien. Aquí hay un gran diagrama en ISL que ilustra esta compensación en varios modelos de capacitación estadística:
"
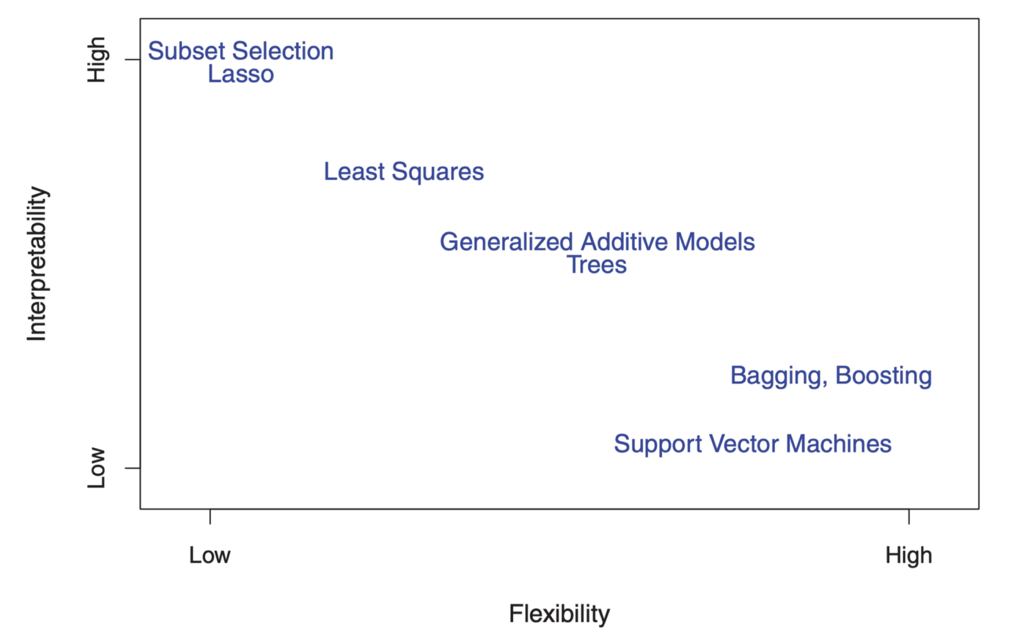
"
Como puede ver, los modelos de aprendizaje automático más flexibles con una mejor precisión de pronóstico, como el método de vector de soporte y los métodos de mejora, al mismo tiempo tienen una baja capacidad de interpretación. El modelado de inferencia también rechaza la precisión del pronóstico del modelo interpretado, haciendo una suposición segura sobre la forma funcional f.
Identificación causal y razonamiento contrafactual
Pero espera un momento! Incluso si usa un modelo bien interpretado con buen ajuste, aún no puede usar estas estadísticas como una evidencia separada de causalidad. Esto se debe al viejo y cansado cliché "la correlación no es causalidad".
Aquí hay un
buen ejemplo : suponga que tiene datos sobre la longitud de cien astas, la longitud de sus sombras y la posición del sol. Usted sabe que la longitud de la sombra está determinada por la longitud del polo y la posición del Sol, pero incluso si establece la longitud del polo como una variable dependiente y la longitud de la sombra como una variable independiente, su modelo seguirá ajustando coeficientes estadísticamente significativos, etc.
Es por eso que las relaciones causales no pueden establecerse solo mediante modelos estadísticos y requieren conocimientos básicos: la supuesta causalidad debe estar justificada por una comprensión teórica preliminar de la relación. Por lo tanto, el análisis de datos y el modelado estadístico de las relaciones de causa y efecto a menudo se basan principalmente en modelos teóricos.
E incluso si tiene una buena justificación teórica para decir que X causa Y, identificar un efecto causal suele ser muy difícil. Esto se debe a que evaluar una relación causal implica identificar lo que sucedería en un mundo contraactivo en el que X no tuvo lugar, que por definición no es observable.
Aquí hay
otro buen ejemplo : suponga que desea determinar los efectos de la vitamina C en la salud. ¿Tiene datos sobre si alguien está tomando vitaminas (X = 1 si está tomando; 0 - no está tomando), y algunos resultados de salud binarios (Y = 1 si están sanos; 0 - no están sanos) que se ve así:
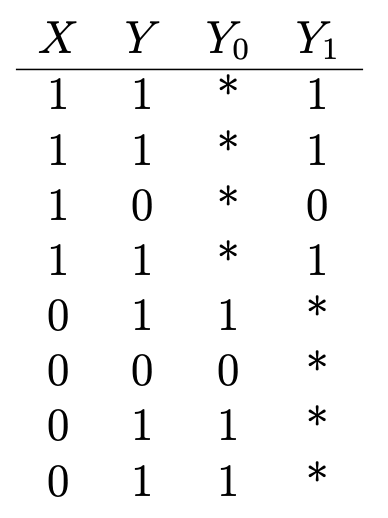
Y₁ es el resultado de salud de quienes toman vitamina C, e Y₀ es el resultado de salud de quienes no lo toman. Para determinar el efecto de la vitamina C en la salud, evaluamos el efecto promedio del tratamiento:
Pero para hacer esto, es importante saber cuáles serían las consecuencias para la salud de quienes toman vitamina C si no tomaran vitamina C, y viceversa (o E (Y₀ | X = 1) y E (Y₁ | X = 0)), que se indican mediante asteriscos en la tabla y representan resultados contrafactuales no observados. El efecto del tratamiento promedio no puede evaluarse secuencialmente sin esta entrada.
Ahora imagine que las personas ya sanas, como regla, intentan tomar vitamina C, pero las personas que ya no son saludables no lo hacen. En este escenario, las evaluaciones mostrarían un fuerte efecto curativo, incluso si la vitamina C en realidad no afectara la salud en absoluto. Aquí, el estado de salud anterior se denomina factor mixto, que afecta tanto la ingesta de vitamina C como la salud (X e Y), lo que conduce a estimaciones distorsionadas. La forma más segura de obtener una puntuación consistent consistente es aleatorizar el tratamiento a través del experimento para que X no dependa de Y.
Cuando el tratamiento se prescribe al azar, el resultado del grupo que no recibe el medicamento, en promedio, se convierte en un indicador objetivo de los resultados contrafácticos del grupo que recibe el tratamiento, y asegura que no haya un factor de distorsión. Las pruebas A / B se guían por esta comprensión.
Pero los experimentos aleatorios no siempre son posibles (o éticos, si queremos estudiar los efectos de fumar o comer demasiadas galletas con chispas de chocolate en la salud), y en estos casos, los efectos causales deben estimarse a partir de observaciones con un tratamiento a menudo no aleatorio.
Existen
muchos métodos estadísticos que identifican los efectos causales en condiciones no experimentales. Lo hacen construyendo resultados contrafácticos o modelando prescripciones aleatorias de tratamiento en datos de observación.
Es fácil imaginar que los resultados de este tipo de análisis a menudo no son muy confiables o reproducibles. Y aún más importante: estos niveles de obstáculos metodológicos no están destinados a mejorar la precisión de la predicción del modelo, sino a presentar evidencia de causalidad a través de una combinación de conclusiones lógicas y estadísticas.
Es mucho más fácil medir el éxito de un pronóstico que de un modelo causal. Aunque existen indicadores de rendimiento estándar para los modelos pronósticos, es mucho más difícil evaluar el éxito relativo de los modelos causales. Pero si es difícil rastrear causa y efecto, no significa que debamos dejar de intentarlo.
El punto principal aquí es que los modelos pronósticos y causales sirven para propósitos completamente diferentes y requieren datos completamente diferentes y procesos de modelado estadístico, y a menudo tenemos que hacer ambas cosas.
Un ejemplo de la industria cinematográfica ilustra: los estudios usan modelos de pronóstico para pronosticar el ingreso bruto de la taquilla, predecir los resultados financieros de la distribución de películas, evaluar los riesgos financieros y la rentabilidad de su cartera de películas, etc. Pero los modelos de pronóstico no nos acercarán a comprender la estructura y la dinámica del mercado de películas y no ayudarán a hacer decisiones de inversión, porque en las primeras etapas del proceso de producción de la película (generalmente años antes de la fecha de lanzamiento), cuando se toman decisiones de inversión, la variación de posible Los resultados son altos.
Por lo tanto, la precisión de los modelos de pronóstico basados en datos iniciales en las primeras etapas se reduce considerablemente. Los modelos predictivos se están acercando a la fecha de inicio de la distribución de películas, cuando la mayoría de las decisiones de producción ya se han tomado y el pronóstico ya no es particularmente factible y relevante. Por otro lado, el modelado de las relaciones de causa y efecto permite a los estudios descubrir cómo diversas características de producción pueden influir en los ingresos potenciales en las primeras etapas de la producción de películas y, por lo tanto, son cruciales para informar sobre sus estrategias de producción.
Mayor atención a las predicciones: ¿Chomsky tenía razón?
Es fácil entender por qué Chomsky está molesto: los modelos pronósticos dominan la comunidad científica y la industria.
Un análisis textual de las preimpresiones académicas muestra que las áreas de más rápido crecimiento de la investigación cuantitativa están prestando cada vez más atención a los pronósticos. Por ejemplo, el número de artículos en el campo de la inteligencia artificial que mencionan "predicción" se ha más que duplicado, mientras que los artículos sobre conclusiones se han reducido a la mitad desde 2013.
Los currículos de ciencia de datos ignoran en gran medida las relaciones de causa y efecto. Y la ciencia de datos en los negocios se centra principalmente en modelos predictivos. Las prestigiosas competencias de campo, como el premio Kaggle y Netflix, se basan en la mejora de los indicadores de rendimiento predictivos.
Por otro lado, todavía hay muchas áreas en las que se presta insuficiente atención al pronóstico empírico, y pueden beneficiarse de los logros obtenidos en el campo del aprendizaje automático y el modelado predictivo. Pero presentar el estado actual de las cosas como una guerra cultural entre el "Equipo Chomsky" y el "Equipo Norvig" es incorrecto: no hay ninguna razón por la que sea necesario elegir una sola opción, porque hay muchas oportunidades para el enriquecimiento mutuo entre las dos culturas. Se ha trabajado mucho para que los modelos de aprendizaje automático sean más comprensibles. Por ejemplo,
Susan Ati de Stanford usa métodos de aprendizaje automático en una metodología de relación causal.
Para terminar con una nota positiva, recuerde los
trabajos de Jude Pearl . Pearl dirigió un proyecto de investigación sobre inteligencia artificial en la década de 1980, que permitió a las máquinas razonar probabilísticamente utilizando redes bayesianas. Sin embargo, desde entonces se ha convertido en el mayor crítico de cómo la atención de la inteligencia artificial exclusivamente a las asociaciones y correlaciones probabilísticas se convirtió en un obstáculo para los logros.
Al compartir la opinión de Chomsky,
Pearl argumenta que todos los logros impresionantes del aprendizaje profundo se reducen a ajustar la curva a los datos. , ( ), 30 . , — « ».
, - , , — , , .
, - , , .
en uno de sus artículos afirma:La mayor parte del conocimiento humano se organiza en torno a relaciones causales más que probabilísticas, y la gramática de cálculo de probabilidad no es suficiente para comprender estas relaciones ... Es por esta razón que me considero solo medio bayesiano.
Parece que la ciencia de datos solo ganará si tenemos más mordiscos.