
Si consideramos los algoritmos de aprendizaje automático de hoy en día con un movimiento desde la ignorancia (abajo) a la conciencia (arriba), entonces los algoritmos actuales son como un salto. Después del salto, hay una desaceleración en la tasa de desarrollo (capacidad de aprendizaje) y un inevitable giro y caída (reentrenamiento). Todos los esfuerzos se reducen a intentos de aplicar la mayor potencia posible al salto, lo que aumenta la altura del salto pero no cambia fundamentalmente los resultados. Al bombear saltos, aumentamos la altura, pero no aprendemos a volar. Para dominar la técnica del "vuelo controlado" será necesario repensar algunos principios básicos.
En las redes neuronales, se utiliza una estructura estática que no permite ir más allá de la capacidad de aprendizaje establecida de toda la estructura. Al fijar el tamaño de la red a partir de un número fijo de
neuronas, limitamos el tamaño de la capacidad de aprendizaje de la red que la red nunca puede pasar por alto. La instalación de una mayor cantidad de neuronas al crear una red le permite aumentar la capacidad de aprendizaje, pero ralentizará el tiempo de aprendizaje. Los cambios dinámicos en la estructura de la red durante el entrenamiento y el uso de datos binarios otorgarán a la red propiedades únicas y eludirán estas limitaciones.
1. Estructura de red dinámica
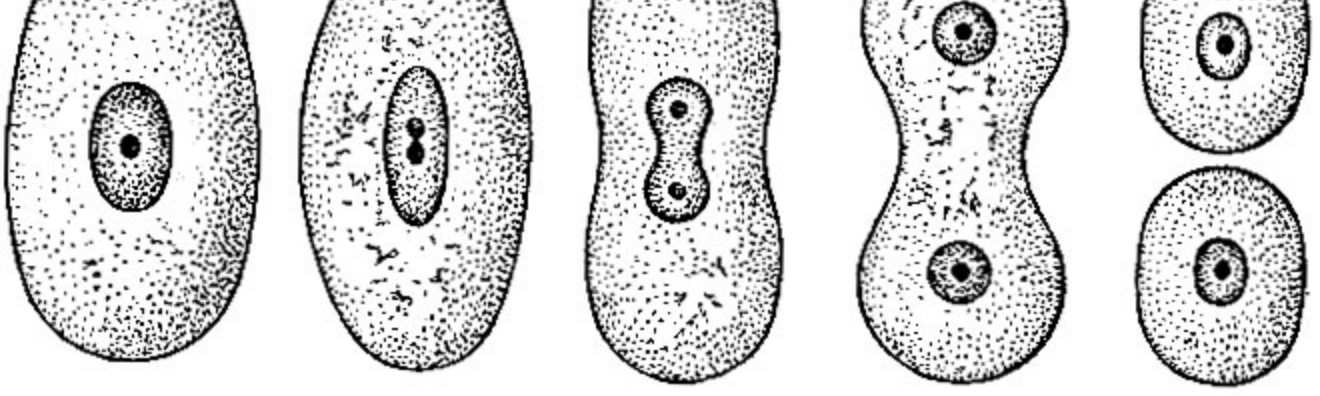
La red misma debe tomar decisiones sobre su tamaño. Según sea necesario, crezca en la dirección correcta aumentando de tamaño. Al crear una red, una neurona, capa o dos, no podemos conocer inequívocamente la capacidad de entrenamiento necesaria de la red y, en consecuencia, su tamaño. Nuestra red debería comenzar desde cero (falta total de estructura) y debería poder expandirse en la dirección correcta de forma independiente cuando lleguen nuevos datos de capacitación.
2. Atenuación de señal
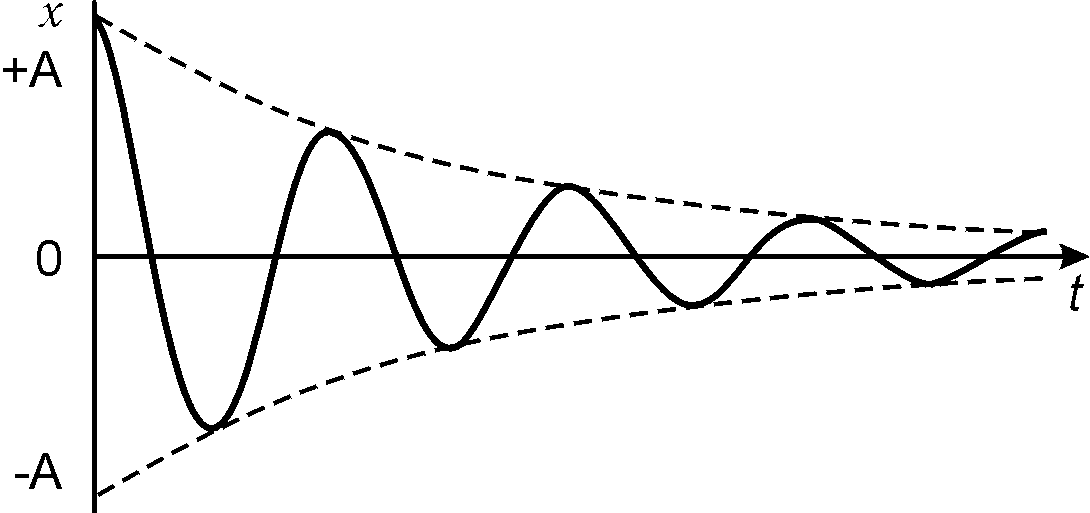
Las redes neuronales involucradas en la suma de la señal utilizan el enfoque "analógico" para el cálculo. Las conversiones múltiples conducen a la atenuación de la señal y su pérdida durante la transmisión. En tamaños de red grandes, los métodos de cálculo "analógicos" inevitablemente conducirán a pérdidas. En las redes neuronales, el problema de la atenuación de la señal puede resolverse mediante redes recurrentes, de hecho, ser una muleta que solo reduce el problema, no lo resuelve por completo. La solución es usar una señal binaria. El número de transformaciones de tal señal no conduce a su atenuación y pérdida durante las transformaciones.
3. Capacidad de aprendizaje en red

Al ampliar la estructura a medida que aprendemos, aumentamos su capacidad de enseñanza. La red misma determina a partir de la tarea en qué dirección desarrollarse y cuántas neuronas se necesitan para resolver el problema. El tamaño de la red limita solo la potencia informática de los servidores y los límites de tamaño del disco duro.
4. Entrenamiento en red
Al cambiar las señales de las redes analógicas a las binarias, tiene la oportunidad de aprender de forma acelerada. El entrenamiento proporciona una configuración inequívoca de la señal de salida. El proceso de aprendizaje en sí cambia solo una pequeña parte de las neuronas, dejando una parte significativa de ellas sin cambios. El tiempo de entrenamiento se reduce muchas veces limitado a cambios en varios elementos de la red.
5. Cálculo de red

Para calcular la red neuronal, necesitamos calcular todos los elementos. Saltarse el cálculo de incluso parte de las neuronas puede conducir al efecto mariposa, donde una señal insignificante puede cambiar el resultado de todo el cálculo. La naturaleza de las señales binarias es diferente. En cada etapa, es posible excluir parte de los datos del cálculo sin consecuencias. Cuanto más grande es la red, más elementos podemos ignorar en los cálculos. El cálculo de los resultados de las redes se reduce al cálculo de un pequeño número de elementos hasta fracciones de un porcentaje de la red. Para el cálculo, un 3,2% (32 neuronas) con una red de mil neuronas, un 0,1% (1 mil) con un millón de "neuronas" en una red y un 0,003% (32 mil) con una red de mil millones de "neuronas" en tamaño son suficientes. Con un aumento en el tamaño de la red, disminuye el porcentaje de neuronas requeridas para calcular.
6. Interpretación de resultados.
En las redes neuronales, los pesos multiplicados por coeficientes hacen que sea imposible establecer una fuente de señal. Todas las señales entrantes de la red neuronal, sin excepción, afectan el resultado, lo que complica la comprensión de las razones que llevaron a su formación. La influencia de las señales binarias en el resultado puede ser cero, parcial o completa, lo que indica claramente la participación de los datos de origen en el cálculo. Los métodos binarios para calcular señales le permiten rastrear la relación de los datos entrantes con el resultado y determinar el grado de influencia de los datos de origen en la formación del resultado.
Todo lo anterior sugiere la necesidad de cambiar los enfoques de los algoritmos de aprendizaje automático. Los métodos clásicos no dan un control completo de la red y una comprensión inequívoca de los procesos que ocurren en ella. Para lograr un "vuelo controlado", es necesario garantizar la fiabilidad de la conversión de la señal dentro de la red y la formación dinámica de la estructura sobre la marcha.