Hola Habr! Les presento la traducción del artículo
"Una explicación intuitiva de las pruebas de hipótesis y los valores P" de Joos Korstanje.
Hace unos años, hice mi primer trabajo de estadística independiente para una empresa de entrega de frutas y verduras. Veinticuatro horas al día, los productos entrantes de los agricultores, antes de ser enviados a los supermercados, pasaron por el departamento de control de calidad. La elección de los productos fue realizada al azar por los empleados de este departamento.
En el informe anual, notaron que la calidad de este año es menor que la calidad del pasado: la diferencia fue de aproximadamente medio punto en una escala del 1 al 10.
Luego me invitaron. Tuve que responder la pregunta:
¿Son estos 0.5 puntos una diferencia significativa?Si no conoce las estadísticas, entonces esta pregunta puede parecerle extraña. Pero no se preocupe: el propósito de este artículo es mostrarle cómo puede responder a esta pregunta utilizando la prueba de hipótesis, también llamada inferencia estadística.
El juego de los números: la contribución de una manzana
Imagine que está comprobando una manzana para bien o para mal, usando una selección aleatoria de manzanas de una caja muy grande con manzanas. En la imagen a continuación vemos el efecto real del tamaño de la muestra en las mediciones: el efecto de una manzana es muy significativo para muestras pequeñas y se vuelve cada vez menos significativo cuanto mayor es el tamaño de la muestra.
La contribución de una manzana depende del tamaño de la muestra.Comprender el efecto del tamaño de la muestra es la primera base para comprender las pruebas de hipótesis. Podemos comenzar a argumentar que 0.5 en 2 manzanas será como una diferencia de 1 manzana, muy pequeña. Pero para 100 manzanas, 0.5 será una diferencia de 50 manzanas: ¡una gran diferencia!
Para muestras pequeñas, 0.5 puntos es una pequeña diferencia, pero para muestras grandes 0.5, esta es una gran diferencia.Qué tan grande debe ser la muestra: prueba de hipótesis y significado como respuesta
Hay varias formas de responder a esta pregunta, pero en este artículo me voy a sumergir en la inferencia estadística o la prueba de hipótesis.
La prueba de hipótesis es una familia de métodos estadísticos utilizados para comprender cómo se puede usar el muestreo de objetos observados para aceptar o rechazar una hipótesis predefinida. Las pruebas de hipótesis se utilizan para resolver muchos problemas, principalmente en la investigación científica y como método clave en el marketing en línea (pruebas A \ B).
Los matemáticos han desarrollado una prueba de hipótesis de tal manera que existe un cierto procedimiento para encontrar la verdad.
La prueba de hipótesis le permite probar solo hipótesis, pero no desarrollarlas.Del cuadro en el que 100 manzanas (llamémosle población), tomamos una muestra de 8 manzanas. Este año, de 8 manzanas, 5 estaban podridas (62%), y en la muestra del año pasado, de 8 manzanas, solo 4 estaban podridas (50%). Queremos usar una prueba de hipótesis para determinar si el porcentaje de manzanas podridas este año es mayor que el año pasado.
La prueba de hipótesis es una alternativa matemática para medir la población. Gracias a estos cálculos, podemos generalizar las mediciones de una pequeña muestra a una gran población. Entonces hacemos menos trabajo.
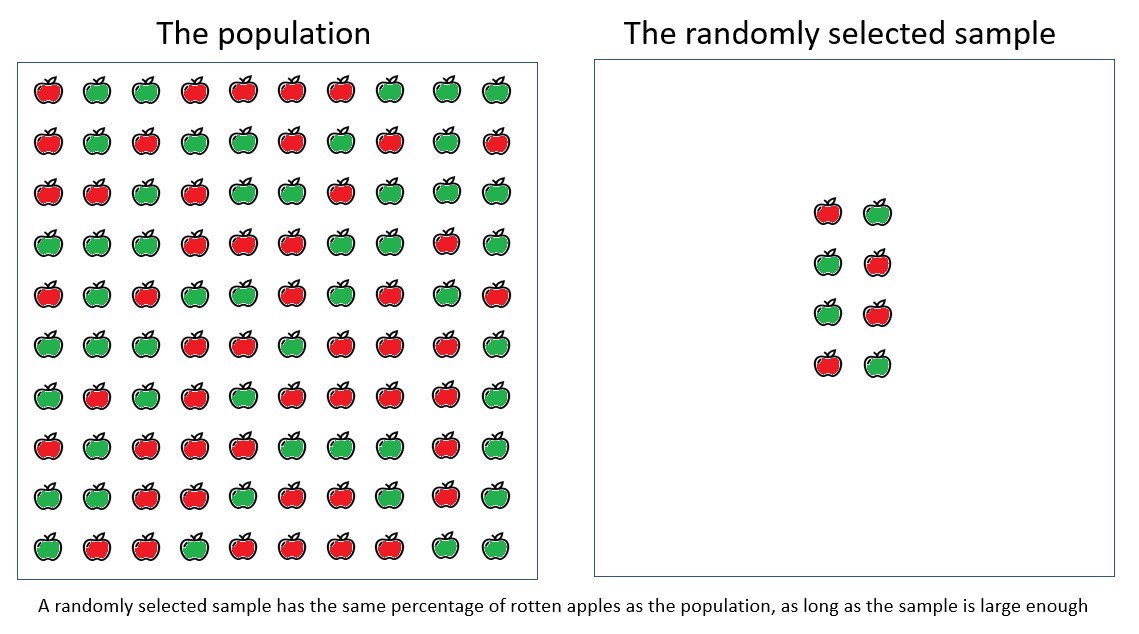
Una muestra muestreada al azar tiene el mismo porcentaje de manzanas podridas que la población general, siempre que la muestra muestreada sea lo suficientemente grande.
Los matemáticos han encontrado una forma de generalizar la conclusión basada en la muestra a la población general.
Este método comienza con la formulación de una hipótesis de investigación clara. Desafortunadamente, las matemáticas solo funcionan si ya tenemos una idea de lo que queremos probar.
La hipótesis principal para nuestro ejemplo:
El porcentaje de manzanas podridas en la población general este año es mayor que en el pasado.Prueba de hipótesis real
La matemática de las pruebas de hipótesis forma un equilibrio entre el resultado de las mediciones de la muestra con el número de observaciones. El resultado es un valor p.Estos cálculos pasan por el uso de distribuciones: para casi todas las situaciones imaginarias, se ha derivado una ley matemática que describe el resultado esperado.
Para preguntas de sí / no, como la pregunta de nuestras manzanas podridas (podrido / no podrido), se aplica la ley de lanzamiento de monedas. Este es el ejemplo más simple de una ley matemática: 50% de colas, 50% de águila.
También se puede representar de manera muy simple como una distribución matemática estándar que nos informa sobre la probabilidad de observaciones. Por ejemplo, 7 águilas cayeron de 10 lanzamientos de monedas. Esto se llama distribución binomial y se puede representar de la siguiente manera:
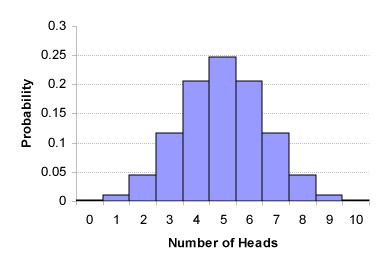Distribución binomial de 10 lanzamientos de monedas.En este artículo estaré lejos de las matemáticas difíciles, pero es importante saber que podemos usar fórmulas matemáticas para evaluar si el porcentaje observado está lejos del porcentaje esperado.
Al final de este artículo, le daré una lista de fórmulas de prueba de hipótesis de uso común para varios casos, y luego le explicaré cómo usarlas. Pero primero, explicaré la interpretación de la prueba de hipótesis.
Resultado de la prueba de hipótesis: valor p
Detrás de la prueba de hipótesis hay un equilibrio matemático entre los valores observados y el tamaño de la muestra. Al final de los cálculos, cada opción de prueba de hipótesis existente producirá una puntuación estandarizada que le permitirá comparar el resultado incluso cuando las matemáticas no sean exactamente las mismas.
El valor P es una forma estándar de formular un resultado de prueba de hipótesis y usarlo en cualquier otra prueba.
El valor P es un número entre 0 y 1 que nos dice si la diferencia está entre nuestras observaciones de las muestras y nuestras hipótesis son muy diferentes. El valor de referencia es 0.05.
La diferencia es estadísticamente significativa si el valor p es menor que 0.05.
Y la diferencia no es estadísticamente significativa si el valor p es mayor que 0.05.
Ejemplo 1:
Hicimos 10 lanzamientos de monedas.
Nuestra hipótesis: esperamos 5 colas.
Nuestras observaciones: tenemos 6 colas.
El cálculo del valor p produjo 0.518, que es más de 0.05.
Nuestra conclusión: la diferencia no es estadísticamente significativa.
Nuestra interpretación: el resultado es consistente con la hipótesis.
Ejemplo 2
Hicimos 10 lanzamientos de monedas
Nuestra hipótesis: esperamos 5 colas.
Nuestro resultado: tenemos 10 colas.
Nuestro valor p es 0.0, que es menor que 0.05.
Nuestra conclusión: la diferencia es estadísticamente significativa
Nuestra interpretación: el resultado no es consistente con la hipótesis.
Ejemplo 3
Verificamos 10 manzanas.
Nuestra hipótesis: esperamos 1 manzana podrida.
Nuestro resultado: tenemos 1 manzana podrida.
Nuestro valor p es 1.0, que es más de 0.05.
Nuestra conclusión: la diferencia no es estadísticamente significativa
Nuestra interpretación: el resultado es consistente con la hipótesis.
Ejemplo 4
Verificamos 10 manzanas.
Nuestra hipótesis: esperamos 1 manzana podrida.
Nuestro resultado: tenemos 5 manzanas podridas.
Nuestro valor p es 0.0114, que es menor que 0.05.
Nuestra conclusión: la diferencia es estadísticamente significativa
Nuestra interpretación: el resultado no es consistente con la hipótesis.
Conclusión
En este artículo, di una interpretación intuitiva de la estructura general de los errores estadísticos o las pruebas de hipótesis. Espero que ahora comprenda mejor las pruebas de hipótesis y cómo puede serle útil.
No profundicé en las pruebas matemáticas y en detalles específicos. La tabla a continuación proporciona una lista de las pruebas de hipótesis más frecuentes que recomiendo para estudios posteriores.
Una lista con hipótesis alternativas para algunas pruebas de hipótesis.
Espero que este artículo le sea útil, y le deseo buena suerte en futuras investigaciones sobre pruebas de hipótesis.