Todos los días, la web global se repone con artículos sobre los algoritmos de aprendizaje automático más populares y más utilizados para resolver diversos problemas. Además, la base de estos artículos, ligeramente modificada en su forma en un lugar u otro, vaga de un investigador de datos a otro. Además, todos estos trabajos están unidos por un postulado generalmente aceptado e indiscutible: la aplicación de uno u otro algoritmo de aprendizaje automático depende del tamaño y la naturaleza de los datos disponibles y de la tarea en cuestión.
Además de esto, los investigadores de datos especialmente insistidos, compartiendo su experiencia, enfatizan:
"La elección de un método de evaluación debería depender parcialmente de sus datos y de lo que, en su opinión, el modelo debería ser bueno" ("Ciencia de datos: información privilegiada para principiantes. Incluyendo lenguaje R, por Cathy O'Neill, Rachel Shutt) .
En otras palabras, un investigador estadístico / de datos debe tener no solo experiencia en el campo temático, sino también una amplia gama de conocimientos variados:
"Un investigador de datos es aquel que tiene conocimiento en las siguientes áreas: matemáticas, estadística, ingeniería informática, aprendizaje automático, visualización, medios de intercambio de datos ... " (del mismo libro). Solo cargando a fondo el conocimiento de las áreas anteriores en la cabeza se puede abordar el aprendizaje automático y encontrar soluciones a los problemas indicados.
En cuanto a mí, este comienzo es bastante adecuado para un libro regular de un kilo y medio sobre ciencia de datos, o un artículo de historia de terror científico con las siguientes fórmulas, símbolos y garabatos de dos pisos "inútiles" que tienen un impacto grave y deprimente en los principiantes en el campo del aprendizaje automático y por casualidad interesados en esta dirección lectores inexpertos, no cargados de "conocimiento necesario". Además, la ronda número 10 de los mismos artículos sobre los 10 algoritmos de aprendizaje automático más populares (
por ejemplo ) solo refuerza el efecto impuesto.
En habr, también se distinguieron :
"La respuesta a la pregunta:" ¿Qué tipo de algoritmo de aprendizaje automático debo usar? "Siempre suena así:" Dependiendo de las circunstancias ". La elección del algoritmo depende del volumen, la calidad y la naturaleza de los datos. Depende de cómo gestiones el resultado. Depende de cómo se crearon las instrucciones para la computadora que lo implementa a partir del algoritmo, y también de cuánto tiempo tiene. Incluso los analistas de datos más experimentados no le dirán qué algoritmo es mejor hasta que lo prueben ".Sin lugar a dudas, todo este conocimiento, así como la perseverancia e interés son necesarios y útiles para lograr buenos resultados no solo en el camino hacia la comprensión del aprendizaje automático, sino también en muchas otras áreas. Además, facilitarán la comprensión de que los algoritmos de aprendizaje automático (en adelante denominados algoritmos) están lejos de ser una docena; pero esto es solo más tarde, con estudio independiente.
Mi objetivo es presentar al lector los algoritmos más utilizados desde un punto de vista práctico y accesible. (El hecho de que no soy un programador y, además, no soy un matemático (¡santo-santo-santo!) Debería subrayar el interés en la narrativa. Educación en ingeniería más experiencia en el "crecimiento del tema" de 10 años (solo algún tipo de número mágico ) - como dicen, y todas mis cosas, todo mi equipaje con el que me fui de frente al aprendizaje automático. Gracias a la experiencia adquirida en la industria petrolera, se encontraron ideas para usar redes neuronales artificiales y algoritmos de aprendizaje automático de inmediato (lea - fueron necesarios conjuntos de datos.) Todo lo que quedaba era tratar Scarlet: aprenda a girar los datos para enviarlos correctamente a la entrada del "programa" y, de hecho, el algoritmo para elegir. Y luego en un círculo vicioso. Observo que mi camino era espinoso y divertido: "balas silbaron sobre mi cabeza" (de m / f "Las aventuras de Funtik"), - pero aun así logré tomar notas, y si se indica interés, en el futuro publicaré otros mensajes).
Por lo tanto, propongo abordar el "mecanizado" por otro lado: ¿por qué no alimentar su conjunto de datos existente (en los ejemplos cargará conjuntos de datos que pueden ser fácilmente entrenados) a muchos algoritmos a la vez, y de acuerdo con los resultados, decida a cuál prestar más atención? estudio cuidadoso posterior y selección de parámetros óptimos que mejoren el resultado. Además, el valor principal del método discutido anteriormente es que sus resultados responderán a la pregunta de lo que vale su conjunto de datos:
"comience por resolver el problema y asegúrese de tener algo que optimizar" (también de algunos entonces las estadísticas insistentes fueron, "respeto" a él, ¡buenos consejos!).
¿Cómo se hace?
Se sabe que la mayor parte de los problemas resueltos con la ayuda de algoritmos se relaciona con los problemas de clasificación (clasificación) y análisis de regresión (análisis predictivo). Por
clasificación se entiende una diferenciación constante de unidades de observación (instancias) de un conjunto de datos a una determinada categoría (clase) en función de los resultados del entrenamiento.
El análisis de regresión es un conjunto de métodos y procesos estadísticos para evaluar la relación entre variables [
Estadísticas: Libro de texto / Ed. prof. M.R. Efimova. - M .: INFRA-M, 2002 ]. El propósito del análisis de regresión es evaluar el valor de una variable de salida continua a partir de los valores de las variables de entrada [
enlace ].
Dejamos de lado el hecho de que el análisis de regresión tiene a su disposición dos métodos diferentes: modelado predictivo y pronóstico. Solo notamos que si hay una serie de tiempo (datos de series de tiempo), usando un modelo de regresión basado en una tendencia explícita, sujeto a la estacionariedad (constancia), se puede realizar un pronóstico. Si las condiciones para la formación de niveles de la serie temporal cambian, es decir, no se observa un proceso no estacionario, entonces depende del modelado predictivo. Particularmente dirigido al dominio completo de ML, propongo leer este artículo en inglés:
enlace . Si surge una discusión sobre esto, estaré encantado de participar en ella.
Dado que las series de tiempo no se utilizarán en los ejemplos de este artículo, el término
pronóstico se refiere al
análisis predictivo .
Para resolver los problemas de clasificación y pronóstico, es adecuado un rango completo de algoritmos, algunos de los cuales consideraremos más adelante. Por conveniencia, el texto posterior se dividirá en dos partes: en la primera consideramos los algoritmos de clasificación más comunes, la segunda la dedicamos a los algoritmos de análisis de regresión. Para cada parte, se presentará un conjunto de datos de "juguete" cargado desde
la biblioteca scikit-learn (v0.21.3):
conjunto de datos de dígitos (clasificación) y el
conjunto de datos del precio de la vivienda de Boston (regresión) , así como enlaces a cada algoritmo de biblioteca scikit-learn para autoexamen y, posiblemente, estudio.
Todos los ejemplos de código se ejecutan en la consola
IDE Spyder 3.3.3 en Python 3.7.3.
Problema de clasificación
Primero, importamos los módulos y funciones necesarios que utilizaremos para resolver el problema de la clasificación de datos:
Descargue el conjunto de datos 'dígitos' directamente desde
el módulo 'sklearn.datasets' :
IDE Spyder proporciona una herramienta conveniente "Administrador de variables", que es útil en todo momento para estudiar el aprendizaje automático (al menos para mí), como
otros "trucos" :
Ejecuta el código. En la consola del "administrador de variables", haga clic en la variable del
conjunto de datos . Se muestra el siguiente diccionario:
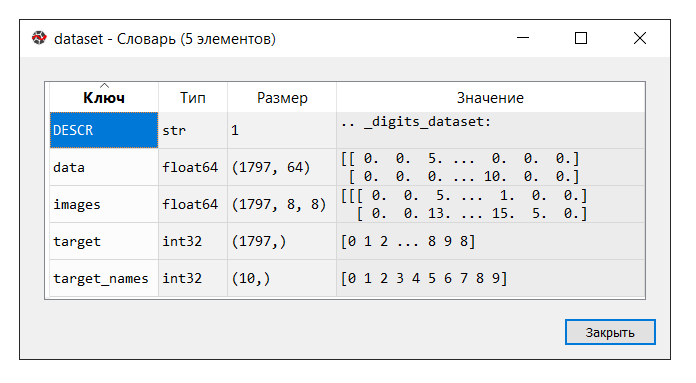
La descripción del conjunto de datos es la siguiente:
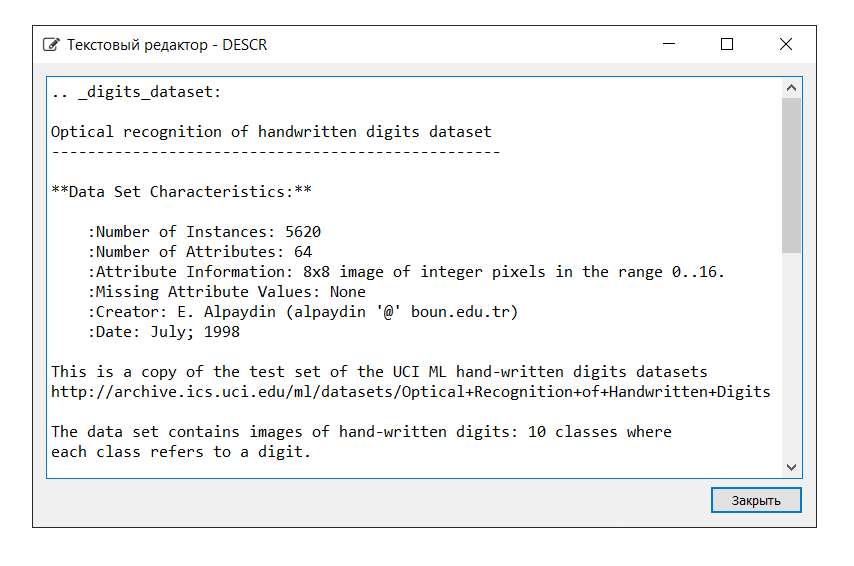
En este ejemplo, no necesitamos la tecla 'imágenes', por lo que asignamos la variable 'datos' a
X , que es una matriz NumPy multidimensional con un conjunto de atributos, 1797 filas en 64 columnas, y la variable
Y a 'target', una matriz multidimensional NumPy con un marcador para cada cuerda
Luego, dividimos el conjunto de datos en las partes de entrenamiento y prueba, configuramos los parámetros para evaluar los algoritmos (se usa validación cruzada [
uno ,
dos ]), definiendo la 'precisión' métrica en el parámetro 'puntuación' [
enlace ]. La precisión es la proporción de objetos correctamente clasificados en relación con el número total de objetos. Cuanto más cercano sea el resultado a 1, mejor [
enlace ]. Además, en uno de los libros se encontró que los resultados de 0.95 (o 95%) y superiores se consideran excelentes.
Deje que las variables
X_train e
Y_train se utilicen para fines de entrenamiento,
X_test e
Y_test para el desarrollo de valores de pronóstico. En este caso, la variable
Y_test no
está involucrada en el cálculo del pronóstico: usando el método de 'puntaje', que es el mismo para cada uno de los algoritmos presentados a continuación, calcularemos las respuestas correctas usando la métrica de 'precisión'. Esto nos permitirá juzgar cómo el algoritmo hace frente a la tarea. No discuto, por nuestra parte, es tan humanamente vil no pedirle al auto las respuestas correctas, sino cómo verificar su rendimiento.
A continuación se muestra una lista de algoritmos con los que alimentamos el conjunto de datos. Con base en los resultados de los cálculos, concluiremos qué algoritmo (cuál de los algoritmos) muestra la mayor eficiencia. Este método bien puede llamarse una
"prueba blitz de algoritmos de aprendizaje automático" (en adelante, prueba blitz).
Para mayor comodidad, la información se abreviará junto a cada algoritmo. Cabe señalar que la configuración de cada algoritmo se acepta de forma predeterminada (predeterminado), con la excepción de algunos puntos, para proporcionar condiciones iguales.
Algoritmos Lineales:
- Regresión logística * /
Regresión logística ('LR')
* La palabra "regresión" puede ser confusa. Pero no olvide que la "Regresión logística" es un algoritmo de clasificación.-
Análisis discriminante lineal ('LDA')
Algoritmos no lineales:
- Método de k-vecinos más cercanos (clasificación) /
K-Neighbours Classifier ('KNN')
-
Clasificador de árbol de decisión ('CARRITO')
-
Clasificador ingenuo de Bayes ('NB')
- Método de
clasificación de vectores de soporte lineal (Clasificación) /
Clasificación de vectores de soporte lineal ('LSVC')
- Método de
vector de soporte (Clasificación) /
Clasificación de vector de soporte C ('SVC')
Algoritmo de red neuronal artificial:
-
Perceptrón multicapa /
Perceptrones multicapa ('MLP')
Algoritmos de conjunto:
- Bagging (clasificación) /
Bagging Classifier ('BG') (Bagging = Bootstrap agregándose)
-
Clasificación aleatoria del bosque ('RF')
-
Clasificador de árboles extra ('ET')
- AdaBoost (clasificación) /
AdaBoost Classifier ('AB') (AdaBoost = Adaptive Boosting)
- Gradiente de
refuerzo (clasificación) /
Gradient Boosting Classifier ('GB')
Por lo tanto, la lista de 'modelos' contiene los siguientes modelos:
models = [] models.append(('LR', LogisticRegression())) models.append(('LDA', LinearDiscriminantAnalysis())) models.append(('KNN', KNeighborsClassifier())) models.append(('CART', DecisionTreeClassifier())) models.append(('NB', GaussianNB())) models.append(('LSVC', LinearSVC())) models.append(('SVC', SVC())) models.append(('MLP', MLPClassifier())) models.append(('BG', BaggingClassifier(n_estimators=n_estimators))) models.append(('RF', RandomForestClassifier(n_estimators=n_estimators))) models.append(('ET', ExtraTreesClassifier(n_estimators=n_estimators))) models.append(('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME'))) models.append(('GB', GradientBoostingClassifier(n_estimators=n_estimators)))
Como ya se mencionó, la efectividad de cada algoritmo se evalúa mediante validación cruzada. Como resultado, se muestra un mensaje (msg - abreviatura del mensaje) que contiene la siguiente información: nombre del modelo en forma de abreviatura, puntaje promedio de validación cruzada 10 veces en los datos de entrenamiento ('precisión' métrica), la desviación estándar se muestra entre paréntesis , así como el valor de la métrica de "precisión" en los datos de prueba.
Después de ejecutar el código, obtenemos los siguientes resultados:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968
Gráfico de extensión (
"caja con bigote" ) (diagrama o diagrama de caja y bigotes, diagrama de caja):
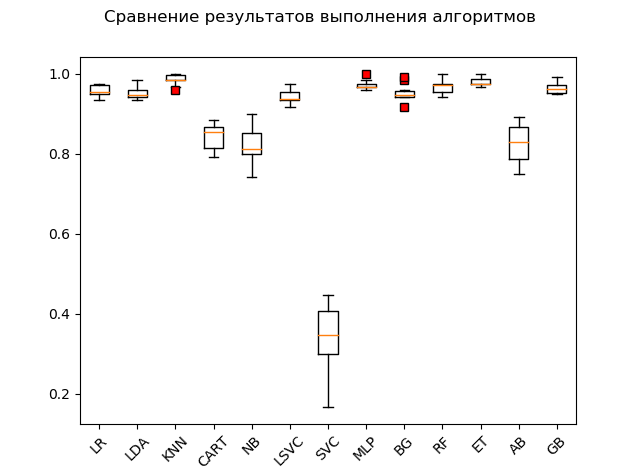
Como resultado de una prueba de bombardeo sobre datos "en bruto", está claro que los más efectivos en los datos de prueba fueron los algoritmos 'KNN' (k-vecinos más cercanos), 'ET' (extra-árboles), 'GB' (gradiente de "impulso"), 'RF' (bosque aleatorio) y 'MLP' (perceptrón multicapa):
KNN: train = 0.985 (0.013) / test = 0.981 ET: train = 0.980 (0.010) / test = 0.975 GB: train = 0.964 (0.013) / test = 0.968 RF: train = 0.968 (0.017) / test = 0.965 MLP: train = 0.972 (0.012) / test = 0.961 LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 BG: train = 0.952 (0.021) / test = 0.941 LSVC: train = 0.942 (0.017) / test = 0.928 CART: train = 0.843 (0.033) / test = 0.830 AB: train = 0.827 (0.049) / test = 0.823 NB: train = 0.819 (0.048) / test = 0.806 SVC: train = 0.343 (0.079) / test = 0.342
Sin embargo, muchos algoritmos son muy exigentes con los datos que se sirven. Por lo tanto, uno de los pasos necesarios es la llamada preparación preliminar de datos (procesamiento previo de datos [
enlace ])
Sin embargo, sucede que el algoritmo muestra los mejores resultados sin un procesamiento preliminar. De ahí la siguiente recomendación: incluir en la prueba blitz varias transformaciones del conjunto de datos original y, después de realizar los cálculos, comparar los resultados para captar la esencia del problema en su conjunto.
Los métodos de preparación de datos preliminares más utilizados son:
-
estandarización;
-
escala (el rango predeterminado es [0, 1]);
-
normalizaciónEstas operaciones con evaluación posterior pueden automatizarse y colocarse en el transportador utilizando la herramienta de
tubería .
Un fragmento de código con la estandarización de los datos de origen es el siguiente:
Observe la adición de '_SS' (abreviatura de StandardScaler) para listar nombres. Esto se hace para no apilar los resultados, así como para verlos cómodamente usando el "administrador de variables" después de realizar las conversiones.
La ejecución de un fragmento de código produce los siguientes resultados:
SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968
Caja de bigote (StandardScaler):
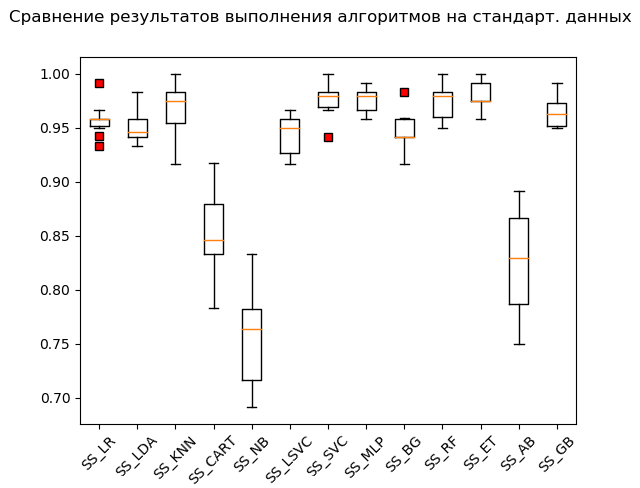
Según los resultados del cálculo en datos estandarizados, los siguientes algoritmos se convirtieron en líderes:
SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_NB: train = 0.756 (0.046) / test = 0.751
Como dicen, de harapos a riquezas: el método del vector de soporte ('SVC'), alimentado por datos estandarizados, hizo el resto, mostrando un excelente resultado. Durante la verificación "manual", al comparar los valores de las variables
Y_test y
predictions_SS [6] , el algoritmo no masticó solo unos pocos valores.
A continuación, se ejecuta el mismo código para las funciones MinMaxScaler (escalado) y Normalizador (normalización). No daré el código completo en el artículo. Puede descargarlo desde mi repositorio en GitHub:
enlace .
¡Solo recuerda pasar un rato y reírte de ti mismo 'solo con fines educativos'! :)
Como resultado, después de revisar todo el código, obtenemos los siguientes resultados:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968 MMS_LR: train = 0.961 (0.013) / test = 0.953 MMS_LDA: train = 0.951 (0.014) / test = 0.946 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_CART: train = 0.850 (0.027) / test = 0.840 MMS_NB: train = 0.796 (0.045) / test = 0.786 MMS_LSVC: train = 0.964 (0.012) / test = 0.958 MMS_SVC: train = 0.963 (0.016) / test = 0.956 MMS_MLP: train = 0.972 (0.011) / test = 0.963 MMS_BG: train = 0.948 (0.024) / test = 0.946 MMS_RF: train = 0.973 (0.014) / test = 0.968 MMS_ET: train = 0.983 (0.010) / test = 0.981 MMS_AB: train = 0.827 (0.049) / test = 0.823 MMS_GB: train = 0.963 (0.013) / test = 0.968 N_LR: train = 0.938 (0.020) / test = 0.919 N_LDA: train = 0.952 (0.013) / test = 0.949 N_KNN: train = 0.981 (0.012) / test = 0.985 N_CART: train = 0.834 (0.028) / test = 0.825 N_NB: train = 0.825 (0.043) / test = 0.805 N_LSVC: train = 0.960 (0.014) / test = 0.953 N_SVC: train = 0.551 (0.053) / test = 0.586 N_MLP: train = 0.963 (0.018) / test = 0.946 N_BG: train = 0.949 (0.016) / test = 0.938 N_RF: train = 0.973 (0.015) / test = 0.970 N_ET: train = 0.982 (0.012) / test = 0.980 N_AB: train = 0.825 (0.040) / test = 0.820 N_GB: train = 0.953 (0.022) / test = 0.956
Resultados 'Top 5':
SS_SVC: train = 0.976 (0.015) / test = 0.990 N_KNN: train = 0.981 (0.012) / test = 0.985 KNN: train = 0.985 (0.013) / test = 0.981 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_ET: train = 0.983 (0.010) / test = 0.981
Por lo tanto, de acuerdo con los resultados de una prueba blitz de algoritmos de aprendizaje automático para resolver el problema de clasificación del conjunto de datos de 'dígitos', los algoritmos de aprendizaje automático más adecuados son: el método k-vecinos más cercanos ('KNN'), el método de vector de soporte ('SVC') y árboles extra ('ET'). Se debe prestar más atención a estos algoritmos para un mayor desarrollo de resultados destinados a aumentar la eficiencia de los cálculos. Todo, como dicen, es solucionable.
Y en esta nota planteada, proceda sin problemas a la segunda parte.
Problema de pronóstico
Nos movemos en el pulgar:
Ejecute el código y trate con el diccionario. La descripción y las claves son las siguientes:
Asignamos los 'datos' clave a la variable
X , que es una matriz NumPy multidimensional con un conjunto de atributos, dimensión 506 filas por 13 columnas, y la variable
Y - 'objetivo', una matriz NumPy multidimensional con un marcador para cada fila.
Dividimos el conjunto de datos en partes de entrenamiento y prueba, configuramos los parámetros para evaluar los algoritmos. En el parámetro 'puntuación' establecemos una de las
métricas 'r2' tradicionales para el análisis de regresión:
R2 - coeficiente de determinación - esta es la proporción de la varianza de la variable dependiente, explicada por el modelo en cuestión (
enlace ).
“El coeficiente de determinación para un modelo con una constante toma valores de 0 a 1. Cuanto más cercano es el coeficiente a 1, más fuerte es la dependencia. Al evaluar modelos de regresión, esto se interpreta como hacer coincidir el modelo con los datos. Para los modelos aceptables, se supone que el coeficiente de determinación debe ser de al menos 50% (en este caso, el coeficiente de correlación múltiple excede el módulo de 70%). Los modelos con un coeficiente de determinación superior al 80% pueden considerarse bastante buenos (el coeficiente de correlación supera el 90%). La igualdad del coeficiente de determinación con la unidad significa que la variable explicada es exactamente descrita por el modelo bajo consideración ” (ibid.).
Para resolver el problema de pronóstico, utilizamos los siguientes algoritmos:
Algoritmos Lineales:
-
Regresión lineal ('LR')
- Regresión de cresta (regresión de cresta) /
Regresión de cresta ('R')
- Regresión del lazo (del inglés LASSO - Operador de selección y contracción menos absoluta) /
Regresión del lazo ('L')
- Método de regresión de
regresión neta elástica ('ELN')
- Método de
regresión de ángulo mínimo (LARS) ('LARS')
- Regresión de cresta bayesiana / Regresión de cresta
bayesiana ('BR')
Algoritmos no lineales:
-
método k regresor de vecinos más cercanos ('KNR')
-
Regresor del árbol de decisiones ('DTR')
-
Máquina de vectores de soporte lineal (regresión) /
Máquina de vectores de soporte lineal - Regresión / ('LSVR')
- Método de
vector de soporte (Regresión) /
Regresión de vector de soporte Epsilon ('SVR')
Algoritmos de conjunto:
- AdaBoost (regresión) /
AdaBoost Regressor ('ABR') (AdaBoost = Adaptive Boosting)
- Bagging (regresión) /
Bagging Regressor ('BR') (Bagging = Bootstrap agregándose)
-
Regresor de árboles extra ('ETR')
- Gradiente de
refuerzo (regresión) /
Gradient Boosting Regressor ('GBR')
-
Clasificación aleatoria del bosque (regresión) /
Clasificación aleatoria del bosque ('RFR')
Por lo tanto, la lista de 'modelos' contiene los siguientes modelos:
models = [] models.append(('LR', LinearRegression())) models.append(('R', Ridge())) models.append(('L', Lasso())) models.append(('ELN', ElasticNet())) models.append(('LARS', Lars())) models.append(('BR', BayesianRidge(n_iter=n_iter))) models.append(('KNR', KNeighborsRegressor())) models.append(('DTR', DecisionTreeRegressor())) models.append(('LSVR', LinearSVR())) models.append(('SVR', SVR())) models.append(('ABR', AdaBoostRegressor(n_estimators=n_estimators))) models.append(('BR', BaggingRegressor(n_estimators=n_estimators))) models.append(('ETR', ExtraTreesRegressor(n_estimators=n_estimators))) models.append(('GBR', GradientBoostingRegressor(n_estimators=n_estimators))) models.append(('RFR', RandomForestRegressor(n_estimators=n_estimators)))
Al igual que con la clasificación, la evaluación de la efectividad de cada algoritmo se realiza mediante validación cruzada. El mensaje que se muestra contiene la siguiente información: el nombre del modelo en forma de abreviatura, el puntaje promedio de una validación cruzada 10 veces en los datos de entrenamiento (métrica 'r2'), la desviación estándar y el coeficiente de determinación r2 en los datos de prueba se muestran entre paréntesis.
Después de ejecutar el código, obtenemos los siguientes resultados:
LR: train = 0.746 (0.068) / test = 0.579 R: train = 0.744 (0.067) / test = 0.570 L: train = 0.689 (0.070) / test = 0.641 ELN: train = 0.677 (0.074) / test = 0.662 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 KNR: train = 0.434 (0.288) / test = 0.538 DTR: train = 0.671 (0.145) / test = 0.637 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003 ABR: train = 0.810 (0.078) / test = 0.763 BR: train = 0.854 (0.064) / test = 0.805 ETR: train = 0.889 (0.047) / test = 0.836 GBR: train = 0.878 (0.042) / test = 0.863 RFR: train = 0.852 (0.068) / test = 0.819
Tabla de alcance:
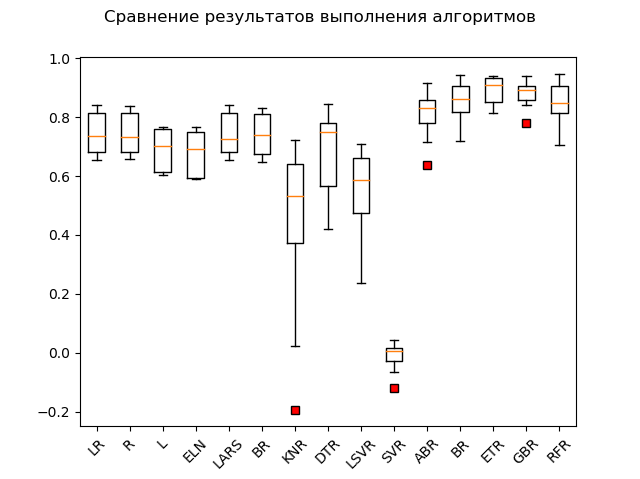
Los líderes obvios son los métodos de conjunto 'GBR' (gradiente 'impulso'), 'ETR' (extra-árboles), 'RFR' (bosque aleatorio) y 'BR' ('ensacado'):
GBR: train = 0.878 (0.042) / test = 0.863 ETR: train = 0.889 (0.047) / test = 0.836 RFR: train = 0.852 (0.068) / test = 0.819 BR: train = 0.854 (0.064) / test = 0.805 ABR: train = 0.810 (0.078) / test = 0.763 ELN: train = 0.677 (0.074) / test = 0.662 L: train = 0.689 (0.070) / test = 0.641 DTR: train = 0.671 (0.145) / test = 0.637 LR: train = 0.746 (0.068) / test = 0.579 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 R: train = 0.744 (0.067) / test = 0.570 KNR: train = 0.434 (0.288) / test = 0.538 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003
Un "adabust", una especie de "loshara", va a la zaga.
Quizás los tres líderes están peinando la estandarización y la normalización. Averigüemos ejecutando el resto del código.
Los resultados son los siguientes:
SS_LR: train = 0.746 (0.068) / test = 0.579 SS_R: train = 0.746 (0.068) / test = 0.578 SS_L: train = 0.678 (0.054) / test = 0.510 SS_ELN: train = 0.665 (0.060) / test = 0.513 SS_LARS: train = 0.744 (0.069) / test = 0.579 SS_BR: train = 0.746 (0.066) / test = 0.576 SS_KNR: train = 0.763 (0.098) / test = 0.739 SS_DTR: train = 0.610 (0.242) / test = 0.629 SS_LSVR: train = 0.727 (0.091) / test = 0.482 SS_SVR: train = 0.653 (0.126) / test = 0.610 SS_ABR: train = 0.811 (0.076) / test = 0.819 SS_BR: train = 0.853 (0.074) / test = 0.813 SS_ETR: train = 0.887 (0.048) / test = 0.846 SS_GBR: train = 0.878 (0.038) / test = 0.860 SS_RFR: train = 0.851 (0.071) / test = 0.818 N_LR: train = 0.751 (0.099) / test = 0.576 N_R: train = 0.287 (0.126) / test = 0.271 N_L: train = -0.030 (0.032) / test = -0.000 N_ELN: train = -0.007 (0.030) / test = 0.023 N_LARS: train = 0.751 (0.099) / test = 0.576 N_BR: train = 0.744 (0.100) / test = 0.589 N_KNR: train = 0.485 (0.192) / test = 0.504 N_DTR: train = 0.729 (0.080) / test = 0.765 N_LSVR: train = 0.182 (0.108) / test = 0.136 N_SVR: train = 0.086 (0.076) / test = 0.084 N_ABR: train = 0.795 (0.053) / test = 0.752 N_BR: train = 0.854 (0.054) / test = 0.827 N_ETR: train = 0.877 (0.048) / test = 0.850 N_GBR: train = 0.852 (0.063) / test = 0.872 N_RFR: train = 0.852 (0.051) / test = 0.801
Como puede ver, los métodos de conjunto todavía están por delante de todos.'Top 5' contiene los siguientes resultados: N_GBR: train = 0.852 (0.063) / test = 0.872 GBR: train = 0.878 (0.042) / test = 0.863 SS_GBR: train = 0.878 (0.038) / test = 0.860 N_ETR: train = 0.877 (0.048) / test = 0.850 SS_ETR: train = 0.887 (0.048) / test = 0.846
:
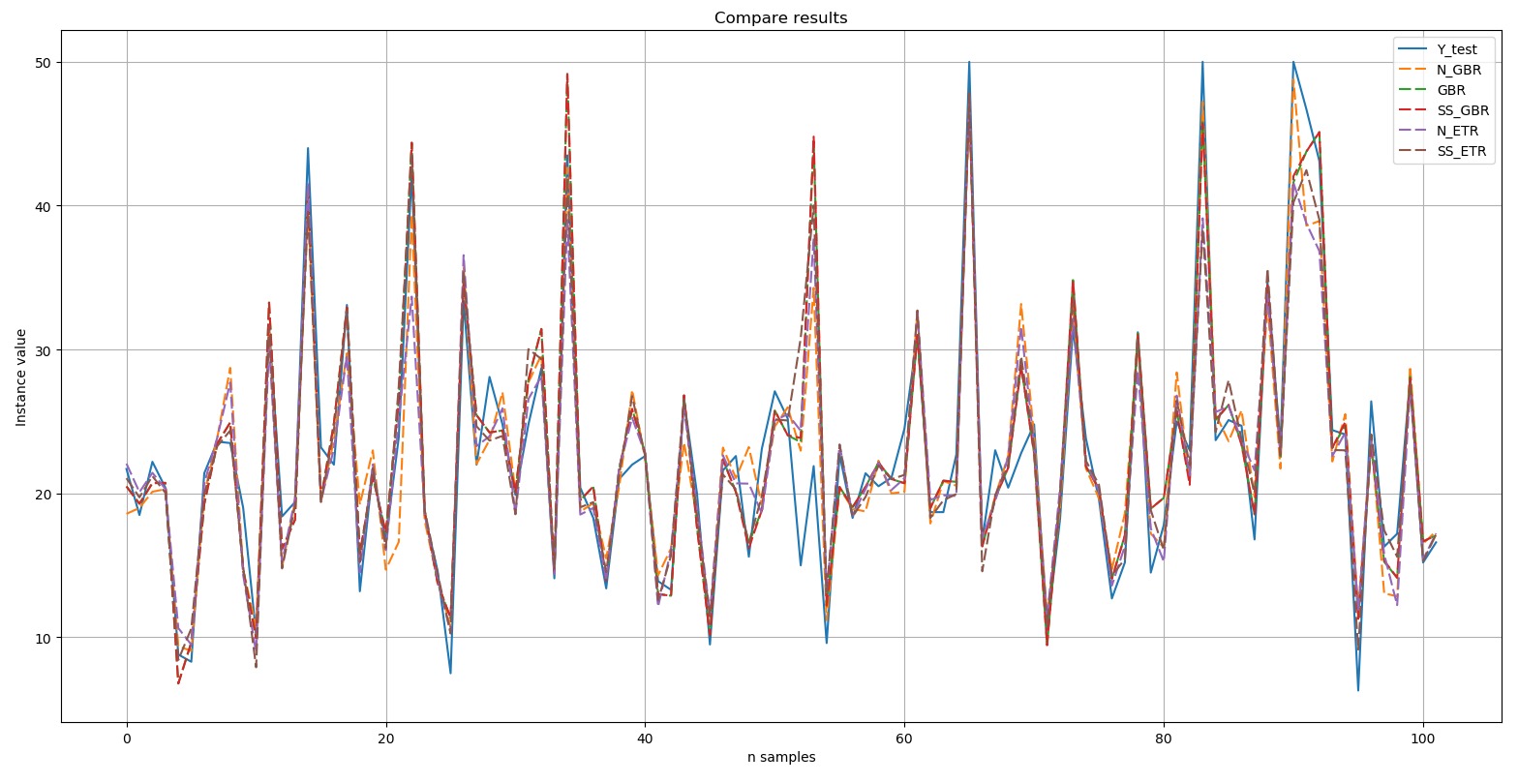Y-test – . , , (dashed). , , .
, Top 5:
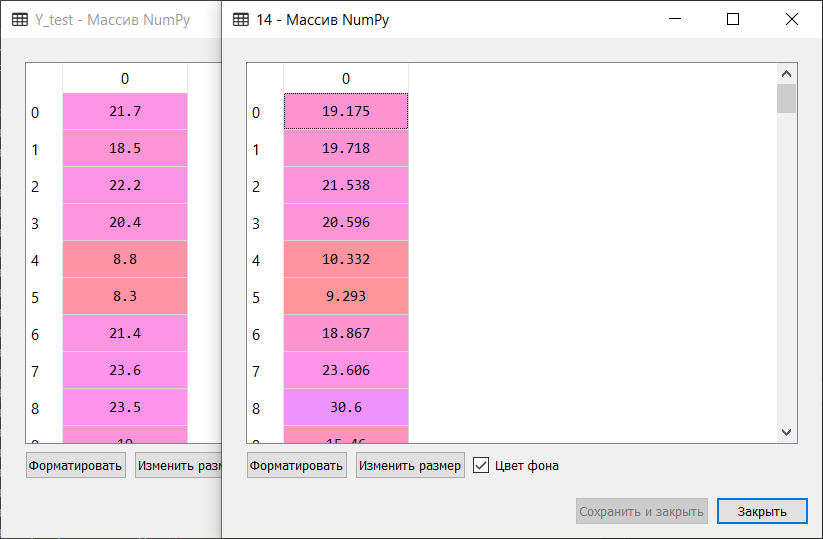
, - 'boston house-price' «» ('GBR') - ('ETR'). .
Epílogo
- (). , 'digits', 10 , 'boston house-price', «» «» .
, , GitHub. :
.
— -. , : . :)
. , , , . , «- », , , , ( ):), ; , ; , «». :)
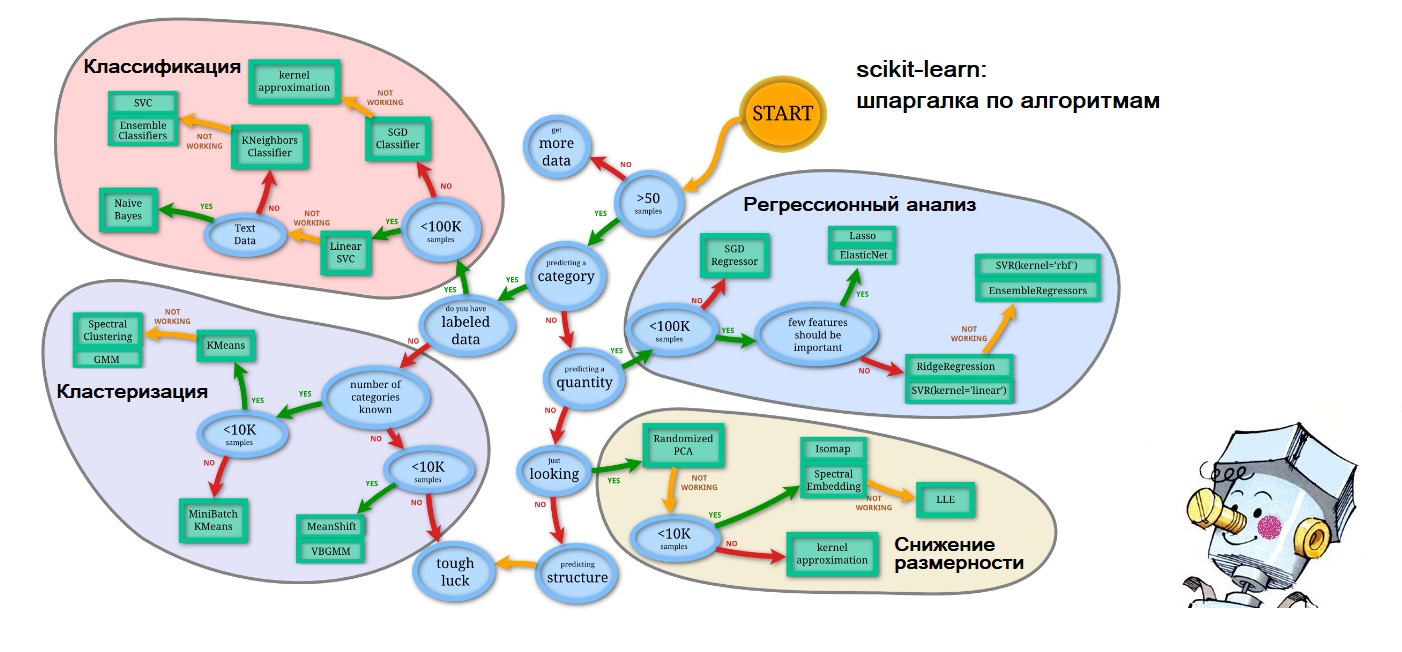
PS , , - : scikit-learn.org (
'Choosing the right estimator' ):
. – .