La hipótesis del primo gemelo es uno de los temas más importantes y complejos en matemáticas. Dos matemáticos resolvieron una versión paralela de este problema para sistemas numéricos pequeños.

El 7 de septiembre, dos matemáticos
publicaron una prueba de una versión de uno de los problemas abiertos más famosos de las matemáticas. El resultado abre un nuevo frente en el estudio de la hipótesis de
los primos gemelos que ha afectado a los matemáticos durante más de cien años y está asociado con algunas de las propiedades más profundas de la aritmética.
"Hemos estado derrapando durante mucho tiempo y nos estamos quedando sin ideas para esta tarea, por lo que es natural que cualquiera tenga nuevas ideas", dijo
James Maynard , un matemático de Oxford.
La hipótesis del primo gemelo se aplica a pares de primos que difieren en 2. Los gemelos son los números 5 y 7. Y 17 y 19. La hipótesis establece que hay un número infinito de tales pares entre los números naturales. Durante la última década, los matemáticos han hecho un progreso significativo, pero aún están muy lejos de ser una solución completa al problema.
Los autores de la nueva evidencia,
Will Savin de la Universidad de Columbia y
Mark Shusterman de la Universidad de Wisconsin en Madison, probaron la hipótesis de un mundo matemático más pequeño pero aún notable. Probaron su validez en el caso de un sistema numérico finito en el que solo hay unos pocos números.
Dichos sistemas numéricos se denominan "campos finitos". A pesar de su pequeño tamaño, conservan muchas de las propiedades matemáticas inherentes a innumerables enteros. Los matemáticos están tratando de encontrar respuestas a preguntas de aritmética en campos finitos, y esperan traducir estos resultados a todos los enteros.
"El sueño final, aunque un poco ingenuo, es que una buena comprensión de las propiedades de un campo finito puede arrojar luz sobre el mundo de los enteros", dijo Maynard.
Además de probar la hipótesis de los primos gemelos, Savin y Shusterman encontraron un resultado aún más sorprendente con respecto al comportamiento de los primos en sistemas numéricos pequeños. Probaron la frecuencia exacta con la que aparecen los primos gemelos a intervalos pequeños, y este resultado hace posible controlar de manera extremadamente precisa un fenómeno como los primos gemelos. Los matemáticos sueñan con lograr resultados similares con números ordinarios; exploran nuevas pruebas en busca de ideas aplicables a los números primos en una recta numérica.
Un nuevo tipo de prima
La predicción más famosa de la hipótesis del primo gemelo es la presencia de un número infinitamente grande de pares de números que difieren en 2. Sin embargo, esta afirmación es más general. Dice que hay un número infinito de primos que difieren en 4 (por ejemplo, 3 y 7), o en 14 (293 y 307), o en cualquier número que especifique.
Alfons de Polignac
hizo esta suposición en su forma moderna en 1849. Durante los siguientes 160 años, los matemáticos no avanzaron mucho con él. Sin embargo, en 2013, el hielo se rompió, o al menos se rompió gravemente. Ese año,
Zhang Ethan demostró la presencia de un número infinitamente grande de pares de números primos, que diferían en no más de 70 millones. El próximo año, otros matemáticos, incluidos Maynard y
Terry Tao , redujeron seriamente esta brecha. El registro actual es la prueba de la existencia de un número infinitamente grande de pares de números primos que difieren entre sí en no más de 246.
Sin embargo, después de eso, el progreso disminuyó. Los matemáticos entienden la necesidad de una idea completamente nueva para resolver completamente este problema. Y los sistemas de números finitos son un buen lugar para buscar esta idea.
Para construir un campo finito, primero debe extraer un subconjunto finito de números a partir de números naturales. Puede, por ejemplo, tomar los primeros cinco números (o cualquier número primo). Y en lugar de representar números en una línea numérica, como de costumbre, imagine un nuevo sistema de números en forma de un dial.
La aritmética, como habrás adivinado, comienza a funcionar en un espacio confinado. ¿Cuál será 4 + 3 en un sistema numérico finito que consta de cinco elementos? Comenzamos con 4, contamos tres divisiones en sentido horario y llegamos a 2. La resta, la multiplicación y la división funcionan de manera similar.

Pero solo hay una trampa. En campos finitos, la definición habitual de primo no tiene sentido. En el campo final, cualquier número se divide por otro. Por ejemplo, 7 generalmente no es divisible por 3. Pero en un campo final de cinco elementos, es divisible. Esto se debe a que en este campo final el número 7 es equivalente al número 12: ambos terminan en la marca 2 del dial. Por lo tanto, 7 dividido por 3 dará lo mismo que 12 dividido por 3, y 12 dividido por 3 dará 4.
Por lo tanto, la hipótesis de los primos gemelos para campos finitos se refiere a polinomios simples, expresiones matemáticas como, por ejemplo, x
2 + 1.
Supongamos, por ejemplo, que su campo final contiene los números 1, 2 y 3. Estos números serán los coeficientes del polinomio en este campo finito, y el polinomio "simple" será uno que no puede descomponerse en factores polinomiales. Por lo tanto, x
2 + x + 2 será simple, ya que no se puede factorizar, pero x
2 - 1 no lo será: este es el producto de (x + 1) y (x - 1).
Habiendo definido polinomios simples, es natural hacer una pregunta sobre polinomios gemelos simples: pares de polinomios que son simples y difieren en un valor fijo. Por ejemplo, el polinomio x
2 + x + 2 es simple, como x
2 + 2x + 2. Se diferencian por x.
La hipótesis de polinomios gemelos simples para campos finitos indica la existencia de un número infinitamente grande de pares de polinomios gemelos simples que difieren no solo por x, sino por cualquier valor.
Cortes limpios
Los conceptos de campos finitos y polinomios simples pueden parecer exagerados e inútiles para estudiar las propiedades de los números. Pero se ven como un simulador de huracanes: un universo en sí mismo, que da ideas sobre fenómenos que tienen lugar en un gran mundo.
"Existe una antigua analogía entre enteros y polinomios, que le permite convertir problemas potencialmente extremadamente complejos relacionados con enteros en tareas relacionadas con polinomios, que también son potencialmente complejos, pero pueden ser más fáciles de resolver", dijo Shusterman.
Los campos finitos se hicieron famosos en 1940 cuando
Andre Weil desarrolló la forma exacta de traducir la aritmética de los sistemas de números pequeños en la aritmética de los enteros. Weil usó esta conexión con resultados sorprendentes. Él
demostró , quizás, el problema más importante en matemáticas: la hipótesis de Riemann, para el caso con un conjunto de curvas sobre campos finitos (este problema se conoce con el nombre de hipótesis geométrica de Riemann). Esta prueba, junto con un conjunto de
hipótesis de Weyl adicionales
, convirtió los campos finitos en un rico paisaje para descubrimientos matemáticos.
La idea clave de Weil era que en campos finitos, se pueden usar técnicas geométricas para encontrar respuestas a preguntas sobre números. “Esta es una característica de los campos finitos. Muchas de las tareas que desea resolver se pueden reformular geométricamente ", dijo Shusterman.
Para comprender cómo aparece la geometría en dicho entorno, imagine cada polinomio como un punto en el espacio. Los coeficientes de un polinomio sirven como coordenadas que determinan su ubicación. Volviendo a nuestro campo final de 1, 2 y 3, el polinomio 2x + 3 se encuentra en el punto (2, 3) del espacio bidimensional.
Pero incluso en el espacio finito más simple hay un número infinito de polinomios. Se pueden crear polinomios más complejos aumentando el exponente del exponente más grande, o grado de expresión. En nuestro caso, el polinomio x
2 - 3x - 1 estará representado por un punto en el espacio tridimensional. Y el polinomio 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 estará representado por un punto en el espacio de ocho dimensiones.
En el nuevo trabajo, este espacio geométrico representa todos los polinomios de un grado dado para un campo finito dado. La pregunta se convierte en la siguiente: ¿hay alguna manera de aislar todos los puntos que denotan polinomios simples?
La estrategia de Savin y Shusterman es dividir el espacio en dos partes. En una parte habrá todos los puntos correspondientes a polinomios con un número par de factores. En el otro, todos los puntos correspondientes a polinomios con un número impar de factores.
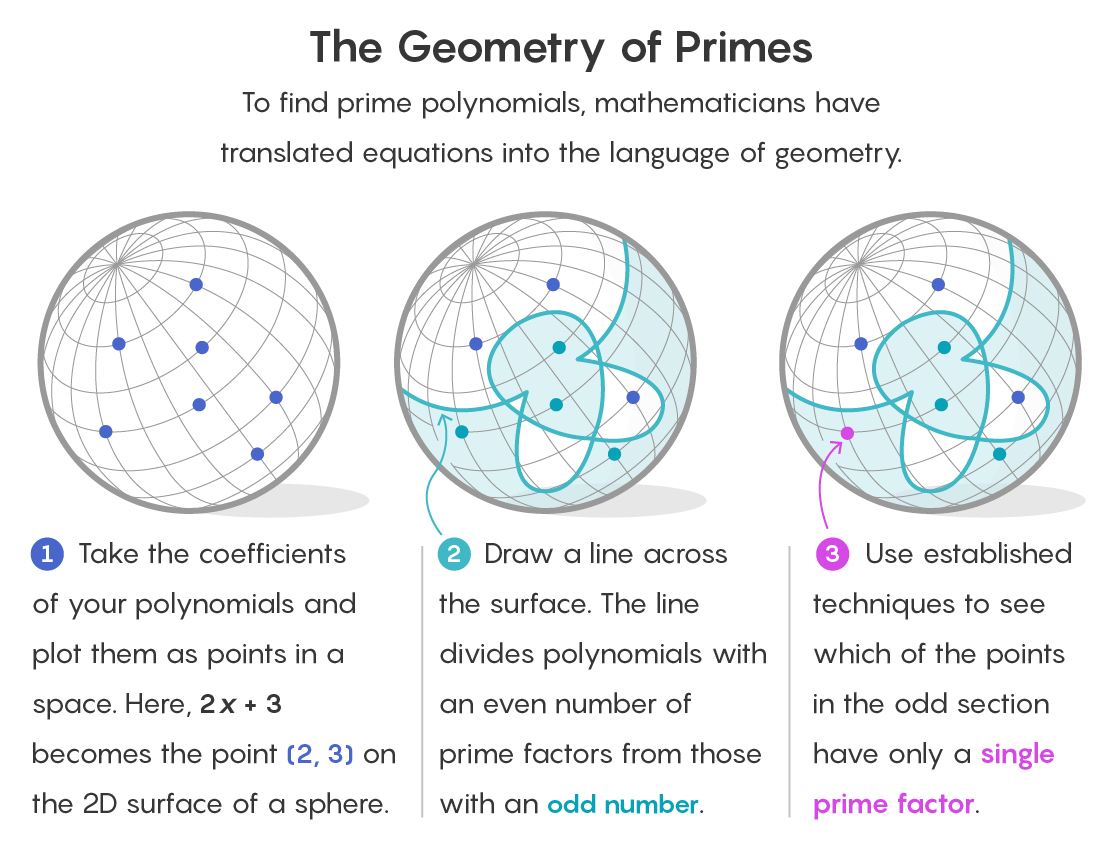
Esto ya simplifica la tarea. La hipótesis de polinomios gemelos simples para campos finitos se aplica solo a polinomios con un factor (al igual que un primo tiene un factor, es en sí mismo). Y dado que el número 1 es impar, parte del espacio que contiene polinomios con un número par de factores puede descartarse inmediatamente.
El truco es usar la división. En el caso de un objeto bidimensional, por ejemplo, la superficie de una esfera, se corta por la mitad mediante una curva unidimensional, tal como el ecuador corta la superficie de la Tierra. Un objeto con una gran cantidad de dimensiones siempre se puede cortar con un objeto con una cantidad menor de una por una.
Pero estas formas con menos dimensiones, que dividen el espacio de los polinomios, no son tan elegantes como el ecuador. Se dibujan de acuerdo con una fórmula matemática llamada
función de Mobius . En la entrada, toma un polinomio, y en la salida da 1 si el polinomio tiene un número par de factores primos, -1 si tiene un número impar y 0 si está factorizado (ya que 16 puede descomponerse en 2 × 2 × 2 × 2).
Las curvas dibujadas por la función de Mobius se doblan y se retuercen como locos, intersectando consigo mismas en muchos lugares. Estos lugares, llamados singularidades, son especialmente difíciles de analizar (corresponden a polinomios que pueden descomponerse en varios factores primos idénticos).
La innovación fundamental de Savin y Shusterman fue que encontraron la forma exacta de cortar bucles con menos mediciones en segmentos más cortos. Estos segmentos fueron más fáciles de aprender que todo el ciclo.
Habiendo compilado un catálogo de polinomios con un número impar de factores primos, y este fue el más difícil, Savin y Shusterman se enfrentaron a la tarea de determinar cuáles son simples y cuáles son gemelos. Para hacer esto, aplicaron varias fórmulas utilizadas por los matemáticos para estudiar los números primos entre los ordinarios.
Savin y Shusterman usaron su técnica para probar dos puntos importantes con respecto a polinomios simples en ciertos campos finitos.
Primero, la hipótesis de los primos gemelos en campos finitos es cierta: hay infinitos pares de polinomios gemelos que difieren en cualquier valor dado.
En segundo lugar, y más importante, este trabajo proporciona un recuento exacto del número de polinomios gemelos simples que se pueden encontrar entre polinomios de cierto orden. Esto es análogo a saber cuántos primos gemelos hay dentro de un intervalo suficientemente largo en una recta numérica, y este es solo el sueño de los matemáticos.
"Este es el primer trabajo que ofrece una analogía cuantitativa de lo que debería ser cierto para los enteros, y este es un resultado realmente sobresaliente", dijo Ziv Rudnik, de la Universidad de Tel Aviv. "Hasta ahora, nada como esto ha sucedido".
La prueba de Savin y Schusterman muestra cómo, casi 80 años después de que Andre Weil demostró la hipótesis de Riemann para curvas sobre campos finitos, los matemáticos todavía se mueven obstinadamente en esta dirección. Ahora, los matemáticos que se ocupan de la hipótesis del primo gemelo recurrirán al trabajo de Savin y Shusterman, y quizás les dará una fuente profunda de inspiración.