👨🏻‍🚒 🕺 🙏🏼 ¿Cuál es el próximo miembro ...? - Estamos buscando una fórmula para el enésimo término de la secuencia, generando funciones y transformación Z 🕌 🏆 🦗

Puede descargar el archivo con el código y los datos en la publicación original en mi blog

Wolfram Language tiene cuatro características completamente asombrosas: FindSequenceFunction , RSolve , DifferenceRootReduce y FindFormula . En este artículo, discutiremos sus capacidades y hablaremos sobre funciones que están estrechamente relacionadas con ellas, para buscar FindLinearRecurrence recursión lineal FindLinearRecurrence (coeficientes de una ecuación de recurrencia lineal) que generan ZTransform GeneratingFunction y ZTransform Z-transform.

La primera función , FindSequenceFunction, busca una expresión para su enésimo miembro por una secuencia de números sin requerir nada más.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n]

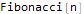
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n]

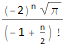La segunda función , RSolve, resuelve ecuaciones de recurrencia de varios tipos. Los elementos pueden parecer

a [f [n]]

$a [f [n]]$ ,

a [f [f [n]]]

$a [f [f [n]]]$ ,

a [f [f [t e x t . . . f [n] t e x t . . .]]]

$a [f [f [\ text {...} f [n] \ text {...}]]]$ , donde f tiene la forma: n + A (ecuaciones de diferencia aritmética), B * n - ecuaciones geométricas o de diferencia q), B * n + a (ecuaciones de diferencia funcional aritmética-geométrica), B * n ^ d (función de potencia geométrica ecuaciones de diferencia), (A * n + B) / (C * n + D) (ecuaciones de diferencia funcional fraccional lineal).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ]

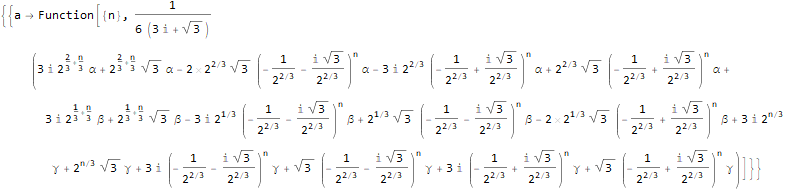
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ]

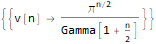La tercera función , DifferenceRootReduce, busca una relación de recurrencia para una secuencia de números, cuyo enésimo miembro tiene una forma determinada.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ]

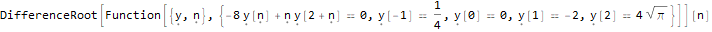
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ]

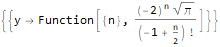
Esta función puede hacer mucho más, por ejemplo, verificar identidades con respecto a secuencias, por ejemplo:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n]

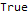
Aquí LucasL es una secuencia de números de Luc (esto es, de hecho, una secuencia de Fibonacci, solo los primeros miembros no son 1, 1, sino 1, 3.

 Hold @ DifferenceRootReduce @ LucasL @ n

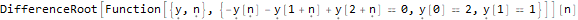
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]]

¿Cómo encontrar una fórmula de recurrencia para una secuencia?

El método de búsqueda para un miembro común de una secuencia a menudo se basa en la necesidad de seleccionar una ecuación de recurrencia.

Puede funcionar de esta manera: busquemos el enésimo miembro de la secuencia en el formulario

f [n] = s u m_{i = 1}^{k} a [i] f [n - i]

$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$ . Tengamos los primeros miembros de la secuencia:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461}

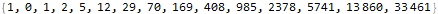
Intentemos encontrar una expresión para el enésimo término en la forma

f [n] = s u m_{i = 1}^{1} a [i] f [n - i] = a [1] f [n - 1]

$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$ :

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ]

 Hold @ Solve @ seauenseEq1

Como puede ver, no hay soluciones.

Intentemos buscar ahora en el formulario

f [n] = s u m_{i = 1}^{2} a [i] f [n - i] = a [1] f [n - 1] + a [2] f [n - 2]

$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$ :

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ]

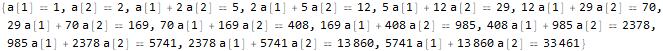
 Hold @ Solve @ seauenseEq2

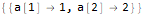
Como vemos, resultó. Por lo tanto, el enésimo término tiene la forma:

f [n] = f [n - 1] + 2 f [n - 2]

$f [n] = f [n-1] + 2f [n-2]$ .

En realidad, hay una función FindLinearRecurrence incorporada que le permite encontrar recursividad lineal, similar a como lo acabamos de hacer:

 Hold @ FindLinearRecurrence @ sequence

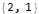
Usando la función LinearRecurrence , puede extender la secuencia:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50]

O combine todo en una línea construyendo una función que: extienda la secuencia, produzca una ecuación de diferencia y encuentre una fórmula general para el enésimo término:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ];

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20]

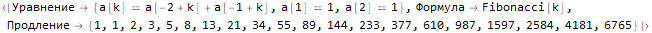
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20]

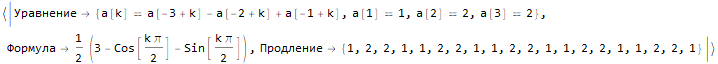
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ]

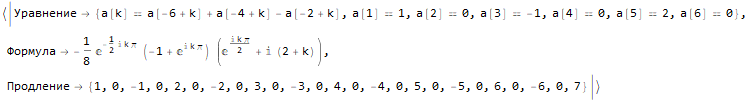
¿Cómo encontrar la fórmula para el enésimo miembro de una secuencia?

Conversión Z

La transformación Z consiste en calcular una serie de la forma

s u m_{n = 0}^{i n f t y} f (n) z^{- n}

$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$ de la función discreta

f (n)

$f (n)$ . Esta transformación nos permite reducir la ecuación de recurrencia para establecer la secuencia en la ecuación para la imagen de la función

f (n)

$f (n)$ , que es similar a la transformada de Laplace, que reduce las ecuaciones diferenciales a las algebraicas.

Así es como funciona:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ]

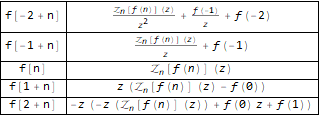
Veamos un ejemplo, digamos, tome la conocida secuencia de Fibonacci:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1};

Está claro que debe reescribirse en la forma, como se muestra a continuación, para que las construcciones como

f (- 1)

$f (-1)$ después de aplicar la transformación Z

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1};

Realizamos la transformación Z:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]]

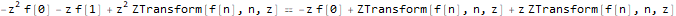
Resolvemos la ecuación para la imagen de la función f - ZTransform [f [n], n, z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ]

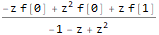
Realizamos la transformación Z inversa, sustituyendo las condiciones iniciales al mismo tiempo (reemplazamos n con n-1 en la expresión final para que nuestra secuencia tenga la indexación correcta (desde el primero, no el término cero):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ]

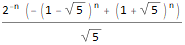
Naturalmente, esto puede automatizarse creando su propia contraparte RSolve:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ];

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ]

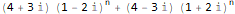
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ]

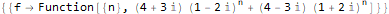
Pero, por supuesto, RSolve contiene muchas más posibilidades para resolver una amplia variedad de ecuaciones discretas, que no analizaremos con más detalle:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ]

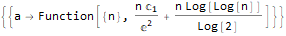
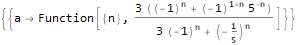
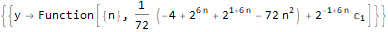
Generando funciones

Función de secuencia generadora

a (n)

$a (n)$ esta es una función

G (x)

$G (x)$ cuya expansión en la serie Taylor (o, más ampliamente, Laurent) tiene la forma:

G (x) = s u m_{i = 0}^{i n f t y} a (n) x^{n}

$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$ . En otras palabras, los coeficientes de potencias de x en la expansión de la función en una serie determinan nuestra secuencia.

Decir función

G (x) = f r a c 1 1 - x

$G (x) = \ frac {1} {1-x}$ es una función generadora de la secuencia 1, 1, 1, 1, ...:

 Series[1 / (1 + -x), {x, 0, 10}]

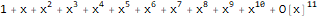
Una función

G (x) = f r a c 1 1 - x - x^{2}

$G (x) = \ frac {1} {1-x-x ^ 2}$ es una función generadora de la secuencia de Fibonacci 1, 1, 2, 3, 5, 8, 13, ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ]

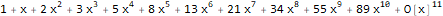
También hay un tipo de función generadora: una función generadora exponencial, que para secuencia

a (n)

$a (n)$ tiene la forma

G (x) = s u m_{i = 0}^{i n f t y} f r a c a (n) n! X^{n}

$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$ .

Digamos, para las secuencias 1, 1, 1, 1 ... y 1, 1, 2, 3, 5, 8, 13, ... las funciones generadoras exponenciales son las siguientes:

e^{x}

$e ^ x$ y

f r a c 1 s q r t 5 e^{- f r a c 2 x 1 + s q r t 5} l e f t (e^{s q r t 5 x} - 1 r i g h t) $

$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ left (e ^ {\ sqrt {5} x} -1 \ right) $$ :

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

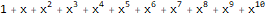
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

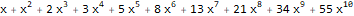
La función de producción en Wolfram Language se puede encontrar mediante dos funciones: GeneratingFunction y FindGeneratingFunction (exponencial con ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}]

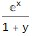
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ]

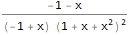
Existen muchos métodos para encontrar un miembro común de una secuencia utilizando funciones generadoras. No haremos hincapié en esto en detalle, digamos, solo una buena teoría está en el sitio web genfunc.ru .

Uno de los métodos es similar a la transformación Z:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ]

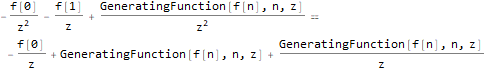
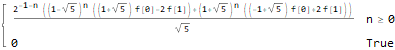
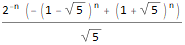
OEIS - Enciclopedia de secuencia de enteros en línea e integración con Wolfram Language

Una colección absolutamente impresionante de secuencias numéricas está disponible en Internet: OEIS (Enciclopedia en línea de secuencias enteras) . Fue creado por Neil Sloan durante su carrera de investigación en AT&T Labs. OEIS almacena información sobre secuencias enteras de interés para aficionados y especialistas en matemáticas, combinatoria, teoría de números, teoría de juegos, física, química, biología, informática. Por el momento, 329085 secuencias se recogen allí. Un registro en OEIS incluye los primeros elementos de una secuencia, palabras clave, descripción matemática, apellidos de los autores, enlaces a la literatura; existe la posibilidad de trazar o reproducir una representación musical de la secuencia. Una búsqueda en la base de datos puede llevarse a cabo por palabras clave y por subsecuencia.

Recientemente, la integración con esta base ha aparecido dentro del Wolfram Language (cuando se usa, es importante comprender que se trata de un desarrollo del usuario; recientemente puede cargar su código en el Repositorio de funciones de Wolfram ). Simplemente ingrese el número de la secuencia que le interesa o una lista de números.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence";

ResourceFunction ["OEISSequence"] : simplemente devuelve los primeros miembros de la secuencia:

 Hold @ OEISSequence @ "A666"

ResourceFunction ["OEISSequenceData"] : emite un conjunto de datos con información completa de la base de datos:

 sequenceData[666] = OEISSequenceData[666, "Dataset"]

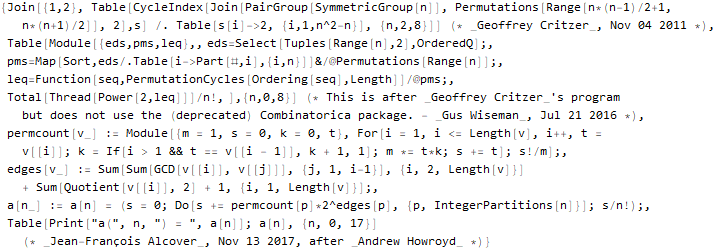
Supongamos que puede "extraer" el código de Wolfram Language:

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"]

O un conjunto de secuencias seleccionadas al azar con información de interés para ellos:

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ];

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ]

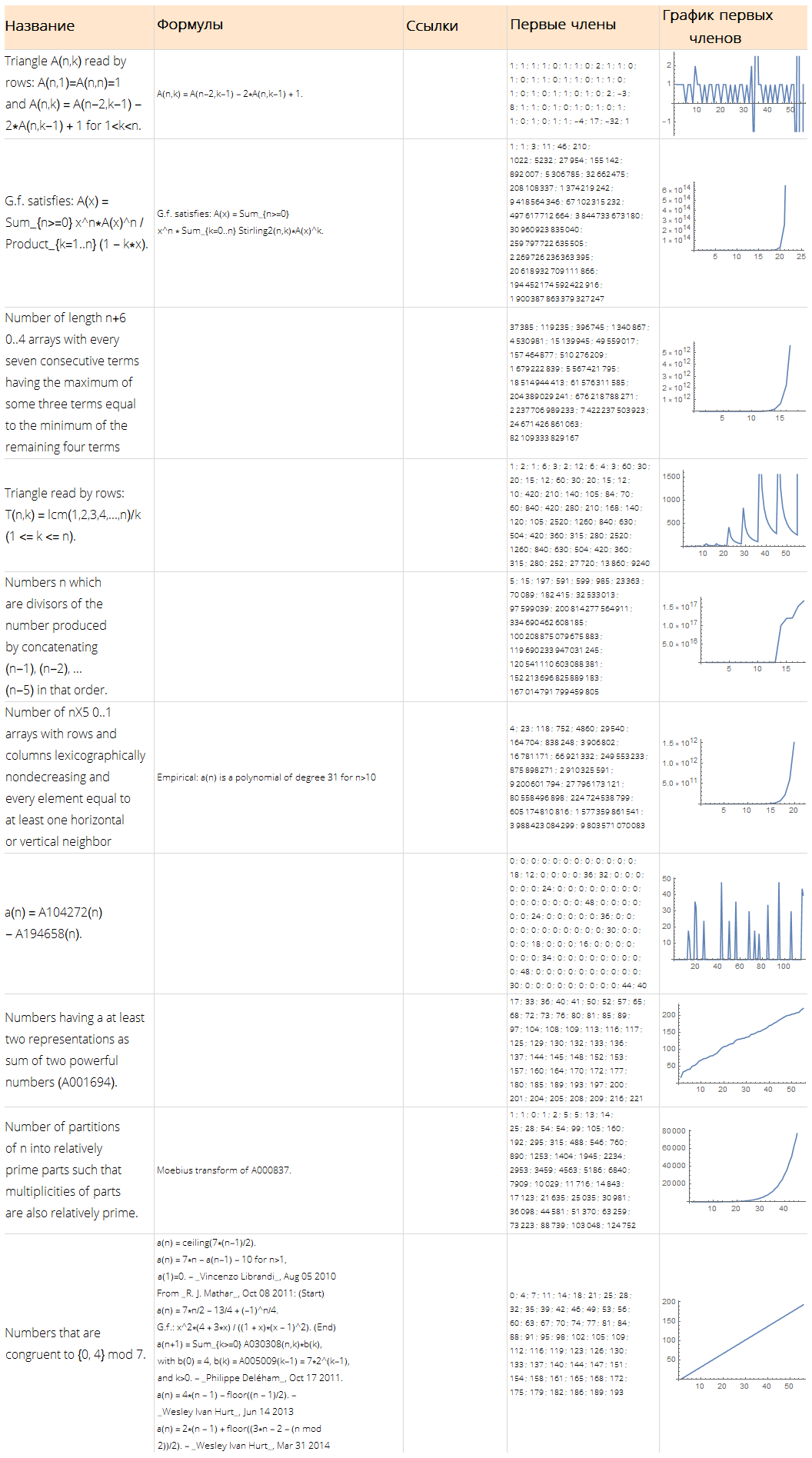
Busca una fórmula potencial

Finalmente, me gustaría mencionar la función FindFormula , que, en base a un conjunto dado de números, crea una fórmula que puede describirlos. Podemos aceptar las dependencias, puede elegir mucho de diferentes clases de funciones.

 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600]

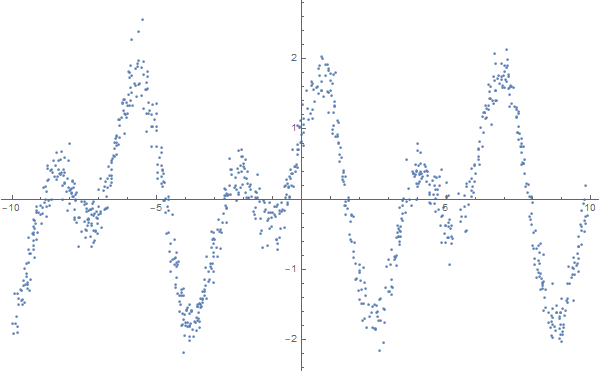
 formulas = FindFormula[data, x]

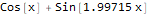
Como puede ver, Wolfram Language seleccionó una función muy cercana a la que se basa en la cual se construyeron los datos "ruidosos", a saber: Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

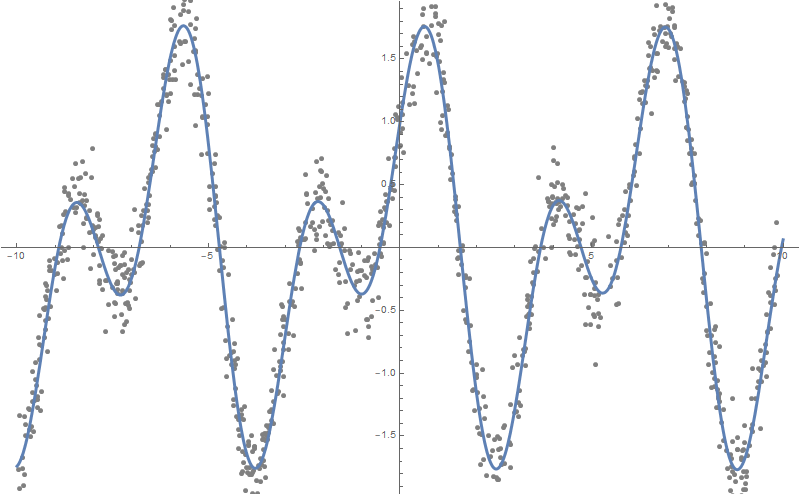
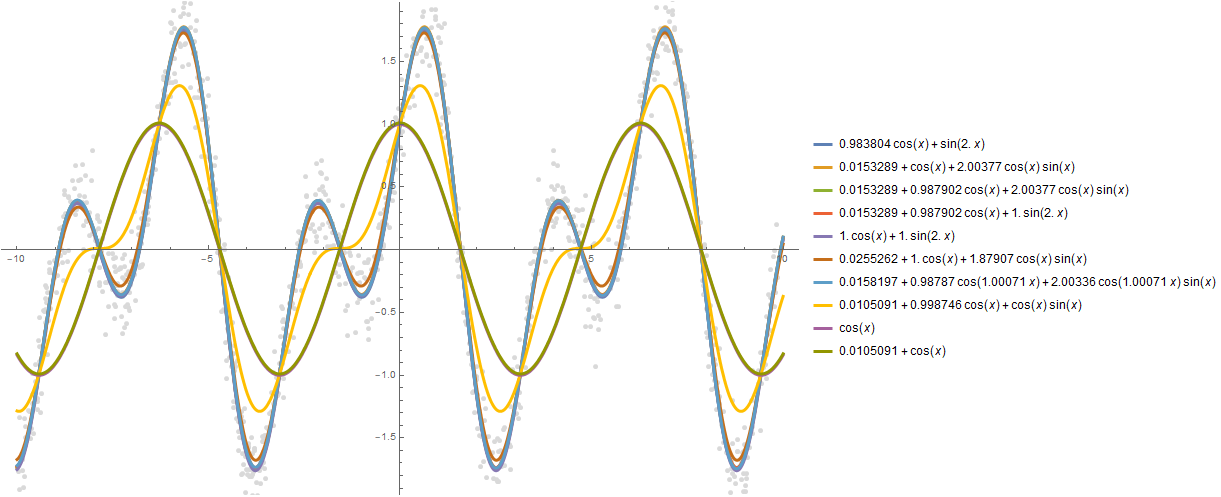
Puede construir más dependencias, digamos 10:

 formulas = FindFormula[data, x, 10]

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

Vale la pena señalar que hay una función similar en funcionalidad que busca una distribución de probabilidad: FindDistribution .

Para cooperación, escriba un mensaje personal en Habré o en mi grupo VKontakte .
Canal de YouTube : seminarios web y videos de capacitación.
Inscripción para nuevos cursos . Curso en línea listo.