La editorial "DMK Press" publicó el libro "Programación de Olimpiadas" con el subtítulo "Estudiar y mejorar algoritmos en competiciones". Se ha convertido en un soplo de aire fresco para todos los interesados, que se preparan y se preparan para participar, o simplemente planean en el futuro, un tipo de actividad tan intelectual como varios eventos de programación deportiva. En Rusia, no están bien familiarizados.
La edición rusa del libro "Guía para la programación competitiva" (Springer International Publishing AG) se publicó con el apoyo del Instituto de Física y Tecnología de Moscú y su jefe Alexei Maleev, Mail.Ru Group, así como el proyecto ICPC de los talleres de Moscú.

“La programación olímpica se está volviendo cada vez más popular cada año entre estudiantes y estudiantes. Un gran ejemplo de esto fue el hecho de que en 2019, nosotros, los Talleres de Moscú ICPC, en noviembre llevaremos a cabo los décimos preparativos del campamento de entrenamiento para la Copa del Mundo en diferentes partes del mundo, ya han pasado en Singapur, Europa y América del Sur y Rusia. de Vladivostok a Moscú. A principios de octubre, el Concurso de Programación de Moscú se celebró en Moscú, en el que participaron 2284 personas en 18 sedes de universidades de Moscú; este es un récord absoluto para la escala de la competencia, que se celebró con el apoyo de Rosmolodezh.
Estamos muy contentos con el vivo interés de los muchachos, y estamos listos para apoyarlo en todos los sentidos; por ejemplo, para los estudiantes de las universidades de Moscú llevamos a cabo una capacitación gratuita para ICPC con la participación de los mejores entrenadores. Y, por supuesto, siempre es útil para los participantes consolidar material, desarmar tareas y mejorar sus conocimientos. Por lo tanto, estoy muy contento de que su libro haya aparecido, y los felicito a todos por esto. Esperamos que en las finales del ICPC en Moscú en junio de 2020 ya haya quienes lo lean y se conviertan en los héroes de la segunda edición complementada ".
Alexey Maleev, Director de la final de la Copa del Mundo ICPC 2020 en Moscú, Vicerrector de MIPT, fundador del proyecto ICPC Workshops de Moscú.
La “Guía para la programación competitiva” se ha traducido al ruso del inglés. Además del inglés y el ruso, se publicó la publicación en coreano.
El autor del libro es Antti Laaxsonen, profesor e investigador de la Universidad de Helsinki Aalto (Finlandia) [3] con amplia experiencia en la enseñanza de programación y algoritmos, y entrenador del equipo de Finlandia en competiciones internacionales de programación. Tiene una alta calificación de 2347 y el estado de "maestro internacional" en el portal Codeforces bajo el apodo de "pllk" [4]. En 2008, él A. Laaxsonen se convirtió en uno de los organizadores de la Olimpiada de Informática en su país. En 2016 - supervisor científico de la Olimpiada Báltica en Informática.
El público objetivo del libro está interesado y / o trabajando en el campo de la programación de la Olimpiada. Pero, para la asimilación completa del material, se requiere conocimiento de los conceptos básicos de programación, mientras que el autor no requiere que el lector experimente el diseño de algoritmos y participe en concursos. Todo esto nos permite recomendar este trabajo a una amplia gama de lectores interesados. Para los principiantes, se convertirá en una introducción a la programación moderna de la Olimpiada, los especialistas experimentados ayudarán a sistematizar el conocimiento y se convertirán en una herramienta de referencia para ellos.
La presentación de material en el libro se lleva a cabo de simple a complejo. Primero, se familiariza con las metas y objetivos del libro, con la programación de la Olimpiada, la colección de tareas CSES [5] y otros libros relevantes sobre la programación de la Olimpiada.
Habiendo recibido la base teórica necesaria, el lector estará listo para continuar con la práctica. La técnica de programación es el siguiente tema. En él, el autor incluyó los conceptos básicos del lenguaje C ++ (estándar C11), que implementa todos los ejemplos del libro; Análisis de algoritmos recursivos y operaciones bit a bit.
En los capítulos del libro, el lector podrá encontrar información sobre la mayoría de los temas "estándar" y ejemplos de implementación de algoritmos que se ofrecen a los participantes en la programación de olimpiadas: estructuras de datos, programación dinámica, algoritmos de gráficos y algoritmos de árbol, consultas de rango y manipulación de filas.
Por separado, me gustaría destacar varios capítulos del libro. Por ejemplo, el capítulo "Preguntas seleccionadas para diseñar algoritmos". Incluía algoritmos con visualización paralela de descargas, análisis de depreciación y búsqueda de los valores mínimos. Al lector se le ofrecen algoritmos para encontrar la distancia de Hamming, la solución del problema de accesibilidad en gráficos, el método de dos punteros, la búsqueda ternaria, la minimización de sumas y otros temas interesantes para la "Olimpiada" y sus entrenadores.
Como ejemplo, daré un ejemplo de tareas del capítulo "Preguntas seleccionadas para diseñar algoritmos".
Consideremos algoritmos con visualización paralela de bits en los que se utilizan operaciones bit a bit para el procesamiento eficiente de datos. En un caso típico, podemos reemplazar el ciclo for con operaciones bit a bit, lo que reduce significativamente el tiempo de ejecución del algoritmo.
Algoritmos de Navegación Paralelos
Los algoritmos con visualización paralela de dígitos se basan en el hecho de que los dígitos individuales de un número pueden manipularse en paralelo mediante operaciones bit a bit. Por lo tanto, uno de los métodos de diseño de algoritmos es presentar los pasos del algoritmo de tal manera que puedan implementarse efectivamente utilizando operaciones bit a bit.
Distancia de Hamming Distancia de Hamming
Hamming (a, b) entre las líneas ayb de la misma longitud es el número de posiciones en las que estas líneas difieren. Por ejemplo:
Hamming (01101, 11001) = 2.
Considere la siguiente tarea: dadas n cadenas de bits de longitud k, calcule la distancia mínima de Hamming entre dos cadenas. Por ejemplo, para las líneas [00111, 01101, 11110], la respuesta sería 2, porque
- Hamming (00111, 01101) = 2;
- Hamming (00111, 11110) = 3;
- Hamming (01101, 11110) = 3.
El problema se puede resolver "de frente" calculando la distancia de Hamming entre cada dos líneas. La complejidad temporal de dicho algoritmo es (n
k) Para calcular la distancia entre las líneas ayb, use la siguiente función:
int hamming(string a, string b) { int d = 0 for (int i = 0; i < k; i++) { if (a[i] != b[i]) d++; } return d; }
Pero como las cadenas consisten en bits, la solución se puede optimizar almacenando cadenas como enteros y calculando la distancia entre ellas mediante operaciones bit a bit. En particular, si k ≤ 32, entonces las cadenas se pueden almacenar como valores de tipo int y para calcular la distancia use esta función:
int hamming(int a, int b) { return __builtin_popcount(a^b); }
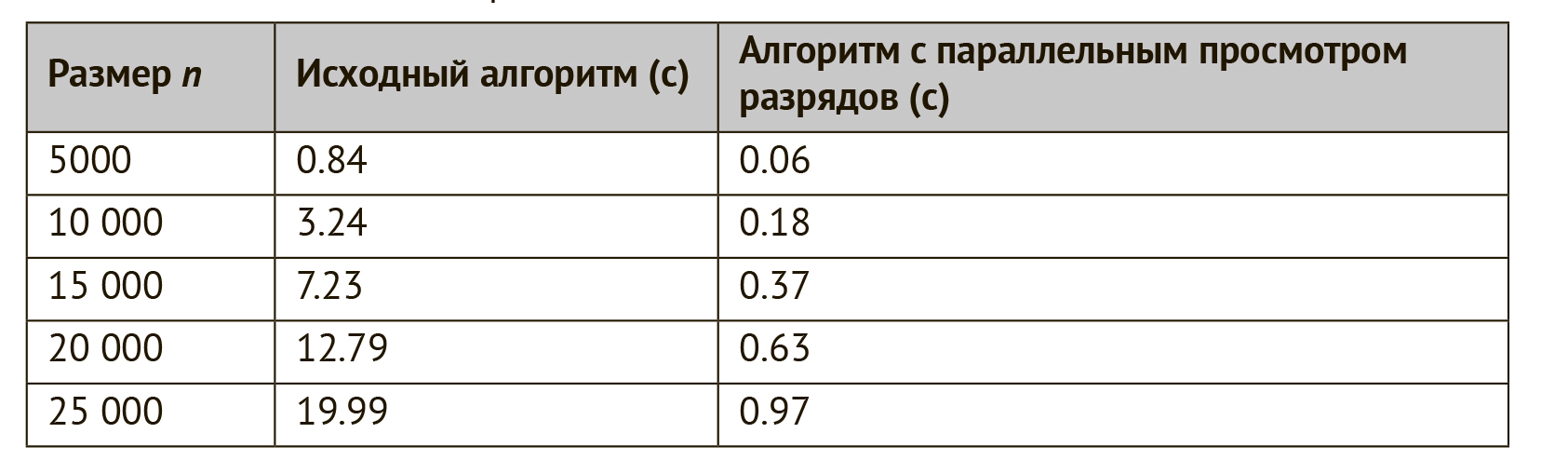
Aquí, la operación EXCLUSIVO O construye una línea en la que las unidades están en aquellas posiciones donde a y b son diferentes. Luego, el número de dígitos unitarios se calcula mediante la función __builtin_popcount. La tabla muestra los resultados de comparar el algoritmo original y el algoritmo con una vista paralela de los bits en términos de tiempo de ejecución en una computadora moderna. El algoritmo con visualización paralela de bits resultó ser aproximadamente 20 veces más rápido.
Tabla: Tiempo de ejecución de algoritmos que calculan la distancia mínima de Hamming para n cadenas de bits de longitud k = 30
Los capítulos "Matemáticas" y "Geometría" no merecen menos atención. Como el lector ya adivinó, se dedican a resolver problemas matemáticos y geométricos mediante el lenguaje de programación C ++ y la construcción de algoritmos apropiados. En el capítulo "matemático", nos esperan cinco grandes temas: "Teoría de números", "Combinatoria", "Matrices", "Probabilidad" y "Teoría de juegos". Y en "geométrico": "Medios técnicos en geometría", "Algoritmos basados en la línea de barrido". Por lo tanto, la presentación compleja de la construcción de algoritmos para resolver problemas matemáticos y geométricos hace que el libro sea un "hallazgo" para el "olympiadniki", porque en el contexto de la escasez de libros sobre este tema, esto es una rareza.
Una serie de problemas, el autor decidió poner en el capítulo "Temas adicionales". Su desarrollo "a veces puede ayudar a resolver los problemas olímpicos más difíciles". Estos son "raíz cuadrada en algoritmos", "Y nuevamente sobre árboles de segmentos", "Duchi", "Optimización de la programación dinámica" y "Varios". Según el nombre de la explicación adicional, requieren subtítulos en árboles de segmentos y en cosas diferentes.
En cuanto a los árboles de segmentos, el lector se familiarizará con la propagación perezosa, los árboles dinámicos, las estructuras de datos en los vértices, los árboles bidimensionales. Y en "Varios" está esperando: una reunión en el medio (dividiendo el espacio de búsqueda en dos partes, aproximadamente iguales, realizando una búsqueda en cada parte y luego combinando los resultados), contando conjuntos, búsqueda binaria paralela, conectividad dinámica.
Complete la información de referencia del libro sobre matemáticas y una extensa bibliografía (32 fuentes).
Entonces, el libro "Programación de Olimpiadas" de Antti Laaxsonen es una excelente introducción al mundo de la programación deportiva. Al mismo tiempo, una maravillosa guía de referencia. El libro es adecuado para principiantes "olympiadnikov" y ayudará a organizar el conocimiento experimentado. Será útil para los entrenadores.
Una vez más, notamos que todos los ejemplos en el libro están implementados en el lenguaje de programación C ++. Él tiene más demanda en los Juegos Olímpicos. Pero alguien puede encontrar esto como un inconveniente del libro, porque otros lenguajes son populares: Python, Java. Quienes prefieren estos lenguajes de programación pueden resolver los problemas propuestos en un libro en su idioma favorito. Este será un buen entrenamiento. En última instancia, es precisamente en la búsqueda de la solución óptima que se completan las tareas de la Olimpiada.
El artículo fue preparado por: Igor Shtompel, autor y presentador de la sección "Carrera / Educación" en la revista
"Administrador del sistema"