Agrega ojos al robot

A veces un robot necesita agarrar algo. Ese robot sin ojos como si no tuviera manos. En el sentido literal. Después de todo, sin saber dónde se encuentra el delicioso, el robot no podrá alcanzarlo con sus brazos robóticos. U otros manipuladores.

En este artículo descubriremos cómo calibrar el robot para poder cambiar entre el Sistema de coordenadas del robot y la cámara 3D.



Paso 1. Toma el robot

Haremos que Dobot Magician mueva elementos. Observe cómo moverá objetos: Intel Realsense D435. Y el objeto de calibración tendrá que ser una bola roja.

Así es como se ven juntos.



La bola roja se elige no solo para que alguien decore el árbol de Navidad . Rojo: para que se pueda encontrar fácilmente en la imagen (sin aprender otra red). Bola: para calcular con mayor precisión su centro en la imagen. Pero volveremos a esto más tarde.

Paso 2. Donde el robot mueve la pelota

El algoritmo de calibración se puede describir de la siguiente manera:

1. Generar una lista de posiciones en el espacio.
2. El robot mueve la pelota por la lista y toma imágenes con ella.
3. Para cada imagen encontramos las coordenadas de la pelota.
4. Calculamos la conversión de coordenadas de cámara a coordenadas de robot.

Las posiciones deben elegirse para cubrir la mayor cantidad de espacio disponible posible. Es mejor no tomar una pelota pequeña, esto reducirá la precisión de la calibración.

No daremos aquí el código para registrar la calibración, ya que depende demasiado del robot, la cámara, el entorno en el que se ejecuta todo (por ejemplo, lo hicimos en ROS). Lo importante es que para una mayor calibración, puede tomar fotos incluso en modo manual, enviando pasos para enviar el robot a posiciones y guardando fotos.

El único requisito es que las posiciones relativas de la cámara y el robot permanezcan sin cambios todo el tiempo. También le recomendamos que tome inmediatamente la segunda serie de imágenes para su validación, para evaluar con qué precisión se calculó la calibración.

Paso 3. Obtenga las coordenadas

Conocemos las coordenadas del manipulador, ya que enviamos especialmente al robot a las posiciones especificadas en la lista. Para los robots con una gran cantidad de grados de libertad, tendrá que especificar más parámetros, pero en nuestro brazo robótico de 4 ejes, la posición está determinada únicamente por las coordenadas de la punta del brazo robótico. Así que simplemente mantenemos esas posiciones en las que se fueron las manos.



Para imágenes de bolas, sus coordenadas aún no se han calculado. Utilizaremos un objeto bien elegido para la calibración. Reformulamos la tarea de encontrar una pelota como "encontrar la región más grande de rojo", que en python + opencv sonará como:

def get_center(image): #       image = cv2.GaussianBlur(image, (7, 7), 0) #     HSV hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) #    saturation = hsv[...,1] saturation[(hsv[..., 0] > 15) & (hsv[..., 0] < 165)] = 0 _, image1 = cv2.threshold(saturation, 92, 255, cv2.THRESH_BINARY) #     contours = cv2.findContours(image1, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)[0] contour = max(contours, key=cv2.contourArea) #    b_circle = cv2.minEnclosingCircle(contour) return b_circle[0] 

Echemos un vistazo más de cerca.

Después de convertir al espacio HSV, la imagen se ve así:



Como puede ver, para los píxeles oscuros, el tono es bastante ruidoso y se necesita un criterio adicional para la segmentación. Deja solo los píxeles rojos $$$\ text {hue} [u, v] \ in [-15; 15]$y mira el canal de saturación. En este canal, la bola de calibración se destaca claramente.

Entonces el criterio final se verá así:

• Verifique que el tono sea aproximadamente rojo
• Deje solo píxeles con saturación por encima de un umbral determinado
• Binariza la imagen

Después de lo cual obtenemos algo como lo siguiente:



Ahora necesitas encontrar las coordenadas del centro de la esfera. Existen diferentes enfoques, por ejemplo, puede personalizar el modelo 3D de la esfera a una nube de puntos. Sin embargo, para el sentido real D435, los valores de profundidad en los bordes de los objetos son bastante ruidosos, por lo que iremos por un camino diferente.

Asumimos que la pelota aquí es el área conectada más grande. Luego encontramos su centro y descubrimos la profundidad hasta este punto en la superficie de la pelota desde la profundidad del canal. Y con un poco de ayuda de la estereometría, pasemos del punto visible en la superficie de la pelota a su centro.

Para encontrar el centro de la pelota, usamos el conocimiento de que la proyección debe ser un círculo, y queremos obtener una estimación imparcial del centro (pero la ventosa del robot está tratando de evitarnos). Aquí es suficiente encontrar un círculo de área mínima que describa esta área, y esto ya se ha decidido en opencv - minEnclosingCircle .

Habiendo recibido las 2 coordenadas del punto u, v en píxeles y la profundidad en milímetros, las traducimos a coordenadas físicas en la cámara SK:

 def get_world_coords(u, v, depth, camera_matrix): f = np.linalg.inv(camera_matrix) l = np.array([u,v,1]) * depth return np.dot(f,l) 

camera_matrix - matriz de parámetros internos de la cámara, de acuerdo con la fórmula .

Paso 4. Realizar la calibración

Por el momento, hemos recibido 2 conjuntos de puntos para diferentes posiciones en el espacio: las coordenadas de la parte superior de la esfera, el punto por el cual la bola aspira al robot en el SC del robot, y las coordenadas del centro visible de la bola, el punto de la esfera más cercana a la cámara, en el SC de la cámara. Para compararlos, primero debe llevarlos a un punto físico de la pelota.

Y la forma más fácil es traducir estos puntos al centro de la pelota. Medimos su radio r = 24 mm. Entonces está claro cómo obtener las coordenadas del centro de la pelota O desde el punto de tangencia K : el toque siempre es 1 radio más alto a lo largo del eje Z.

Queda por traducir las coordenadas del centro V de la región visible en las coordenadas del centro de la bola O. Para explicar cómo hacer esto, use la figura:



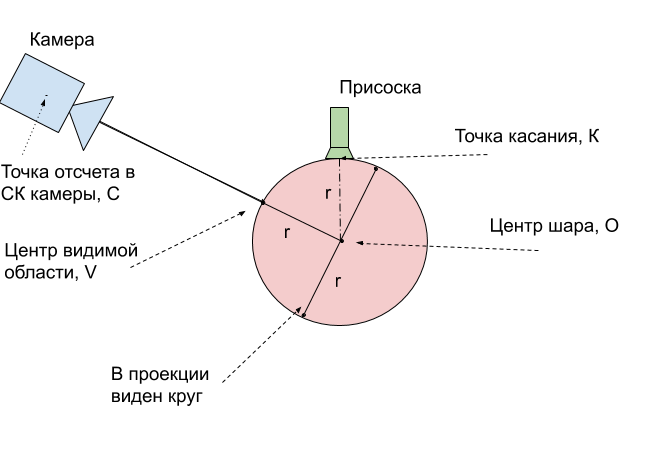
Resulta que el centro real de la bola O siempre es exactamente 1 radio más profundo que el punto visible V. Esto significa que el vector de radio encontrado debe extenderse 24 mm.

$$

$$\ vec {CO} = \ vec {CV} + \ frac {\ vec {CV}} {| \ vec {CV} |} r$$

Sigue siendo bastante importante: tener 2 conjuntos de coordenadas 3D correspondientes a los mismos puntos físicos, encuentre la transformación del primer conjunto al segundo. Utilizaremos la función opencv cv2.estimateAffine3D para esto. Para coordenadas encontradas idealmente, la transformación afín es, por supuesto, la enumeración, para describir la transformación de puntos, la rotación y el desplazamiento son suficientes, la extensión será superflua. Sin embargo, el uso de la transformación afín le permite compensar las imprecisiones con una matriz mal calculada de los parámetros internos de la cámara. Incluso más que eso, le permite obtener una calibración sin conocerlos en absoluto.

 transformation = cv2.estimateAffine3D(camera_coords, robot_coords) 

La salida es una matriz de transformación 3x4, los primeros componentes 3x3 son una matriz de rotación combinada con extensión a lo largo de los ejes. Con la calibración correcta de la cámara y buenos datos de entrada, debe obtener una matriz cercana a la matriz de rotación. Los 3 números restantes son el vector de desplazamiento entre la cámara y el robot.

Paso 5. Usamos calibración

Para utilizar la calibración obtenida, es necesario repetir las transformaciones indicadas. Los llevamos a un solo algoritmo.

1. Encontramos en la imagen RGBD las coordenadas del punto u, v, profundidad de interés para nosotros.
2. Los traducimos a coordenadas físicas x, y, z en la cámara SK usando la matriz de parámetros internos
3. En el caso de una pelota, el punto de interés para nosotros es la profundidad de la pelota. $$$v '= \ frac {| v | + r} {| v |} \ cdot v, v = [x, y, z]$
4. Aplicamos la transformación de transformación encontrada, que denotamos por la matriz T
   $$$v '' = T \ veces [v'_0, v'_1, v'_2, 1] ^ T$
5. Tenemos las coordenadas del centro de la pelota en el robot SK. Para que el robot no intente perforar la pelota, enviamos un punto 1 radio más alto para el control $$$v '' '= [v' '_ 0, v' '_ 1, v' '_ 2 + r]$

Precisión de calibración

Calculamos la calibración en 9 posiciones. En un conjunto de validación de 6 posiciones más, se obtuvo una precisión de 2.5 mm con un área de trabajo de 16x30x5 cm. Para hacer esto, aplicamos la transformación encontrada a las imágenes restantes y calculamos la longitud promedio del vector de error.

Paso 6. Usamos en tareas aplicadas

Una vez realizada la calibración, puede comenzar a resolver problemas reales. Por ejemplo, conectamos un casco de realidad virtual con controladores y pudimos controlar el robot y mover los cubos en realidad virtual.


Pero este método de calibración es bastante general. No importa qué cámara y robot se utilicen, el método descrito facilita el cálculo de la relación entre los sistemas de coordenadas del robot y la cámara. Además, con pequeños cambios, el método es autónomo para que el robot pueda realizar automáticamente la calibración, ya que con el tiempo la cámara se moverá en relación con el robot.

Vasyutka y ZlodeiBaal y yo planeamos seguir hablando sobre el mundo de los robots, la realidad virtual y el aprendizaje automático, si es interesante. Y las fuentes de calibración se pueden encontrar en mi geit .