En previsión del inicio de un nuevo hilo en el curso "Redes neuronales en Python", hemos preparado para usted una traducción de un artículo interesante.
Uno de los principales problemas en la implementación de la nueva generación de computadoras cuánticas radica en su cliente más básico:
qubit . Los Qubits pueden interactuar con cualquier objeto cercano que transfiera
energía cerca de sus propios
fotones errantes (es decir, campos electromagnéticos no deseados,
fonones (vibraciones mecánicas de un dispositivo cuántico) o defectos cuánticos (irregularidades en la superficie del chip que aparecieron durante la etapa de fabricación), que puede cambiar impredeciblemente el estado de los qubits por sí mismos.
El asunto se complica por muchas tareas que ponen las herramientas utilizadas para controlar qubits. Los Qubits se procesan y leen por métodos
clásicos : señales analógicas en forma de campos electromagnéticos, junto con una placa física en la que se construye un qubit, por ejemplo, un microcircuito superconductor. Las imperfecciones en la electrónica de control (que provocan ruido blanco), la interferencia de fuentes de radiación externas y las fluctuaciones en los convertidores digital a analógico conducen a errores estocásticos aún mayores que empeoran el funcionamiento de los microcircuitos cuánticos. Estos problemas prácticos afectan la precisión de los cálculos y, por lo tanto, limitan la aplicación de la próxima generación de dispositivos cuánticos.
Para aumentar el poder de cómputo de las computadoras cuánticas y abrir el camino a la computación cuántica a gran escala, primero es necesario construir modelos físicos que describan con precisión estos problemas experimentales.
En el artículo
"Control cuántico universal a través del aprendizaje de refuerzo profundo" , publicado en la información cuántica de Nature Partner Journal (npj) (https://www.nature.com/npjqi/articles), presentamos una nueva estructura de control cuántico creada mediante el aprendizaje profundo con refuerzo en el que los problemas prácticos de optimizar el control cuántico pueden encapsularse con una sola función de
pérdida . La estructura en consideración proporciona una disminución en el error promedio de la
puerta cuántica a dos órdenes de magnitud en comparación con las soluciones estocásticas estándar de descenso de gradiente y una reducción significativa en el tiempo de puerta a los valores óptimos de los análogos de síntesis de puerta. Nuestros resultados abren nuevos horizontes para el modelado cuántico, la química cuántica y las pruebas de excelencia cuántica utilizando dispositivos cuánticos en el futuro cercano.
La innovación de este paradigma de control cuántico se basa en el desarrollo de una función de control cuántico y un método de optimización eficaz basado en el aprendizaje profundo con refuerzo. Para desarrollar una función de pérdida integral, primero necesitamos desarrollar un modelo físico de un proceso de control cuántico realista en el que podamos predecir con precisión la magnitud del error. Uno de los errores más molestos al evaluar la precisión de la computación cuántica es la fuga: la cantidad de información cuántica perdida durante el cálculo. Tal fuga generalmente ocurre cuando el estado cuántico de un qubit cambia a un nivel de energía más alto o más bajo debido a una emisión espontánea. Debido al error de fuga, no solo se pierde información cuántica útil, sino que también degrada la "cuantidad" y, en última instancia, reduce el rendimiento de una computadora cuántica al rendimiento de una computadora con una arquitectura clásica.
Una práctica común para estimar con precisión la información perdida durante un cálculo cuántico es modelar primero todo el cálculo. Sin embargo, esto niega el objetivo de crear computadoras cuánticas a gran escala, ya que su ventaja es que pueden realizar cálculos imposibles para las computadoras clásicas. Con la mejora del modelado físico, nuestra función de pérdida común nos permite optimizar conjuntamente los errores de fuga acumulados, las violaciones de las condiciones de límite de control, el tiempo total de la válvula y la precisión de la válvula.
Con la nueva función de gestión de pérdidas, el siguiente paso es utilizar una herramienta de optimización efectiva para minimizarla. Los métodos de optimización existentes no son lo suficientemente buenos como para buscar soluciones de alta precisión que sean confiables para controlar las fluctuaciones. En su lugar, utilizamos un método basado en el método de aprendizaje profundo con refuerzo (RL),
RL, un área de confianza . Dado que este método demuestra un buen rendimiento en todas las tareas de prueba, es inherentemente resistente al ruido de la muestra y puede optimizar problemas de control complejos con cientos de millones de parámetros de control. Una diferencia significativa entre este método de RL dentro de la política y los métodos de RL fuera de política previamente estudiados es que la política de gestión se presenta independientemente de la gestión de pérdidas. Por otro lado, todas las políticas de RL, como
Q-learning , utilizan una única red neuronal para representar la ruta de control y la recompensa asociada, donde la trayectoria de control determina las señales de control que deben asociarse con los qubits en diferentes medidas, y la recompensa asociada mide qué tan bueno es el tacto. control cuántico
On-policy RL es bien conocido por su capacidad de usar características no locales en las rutas de control, lo que se vuelve crítico cuando el panorama de control es multidimensional y está repleto de una cantidad combinatoriamente grande de soluciones no globales, como suele ser el caso con los sistemas cuánticos.
Codificamos la ruta de control en una red neuronal totalmente conectada de tres capas, política NN, y la función de pérdida de control en la segunda red neuronal, valor NN, que refleja el premio futuro con descuento. Se obtuvieron soluciones de control confiables con agentes de aprendizaje de refuerzo que entrenan ambas redes neuronales en un entorno estocástico que simula un control de ruido realista. Ofrecemos una solución para controlar un conjunto de compuertas cuánticas de dos qubit continuamente parametrizadas, que son de particular importancia en la aplicación a la química cuántica, pero son demasiado caras de implementar utilizando un conjunto universal estándar de compuertas.
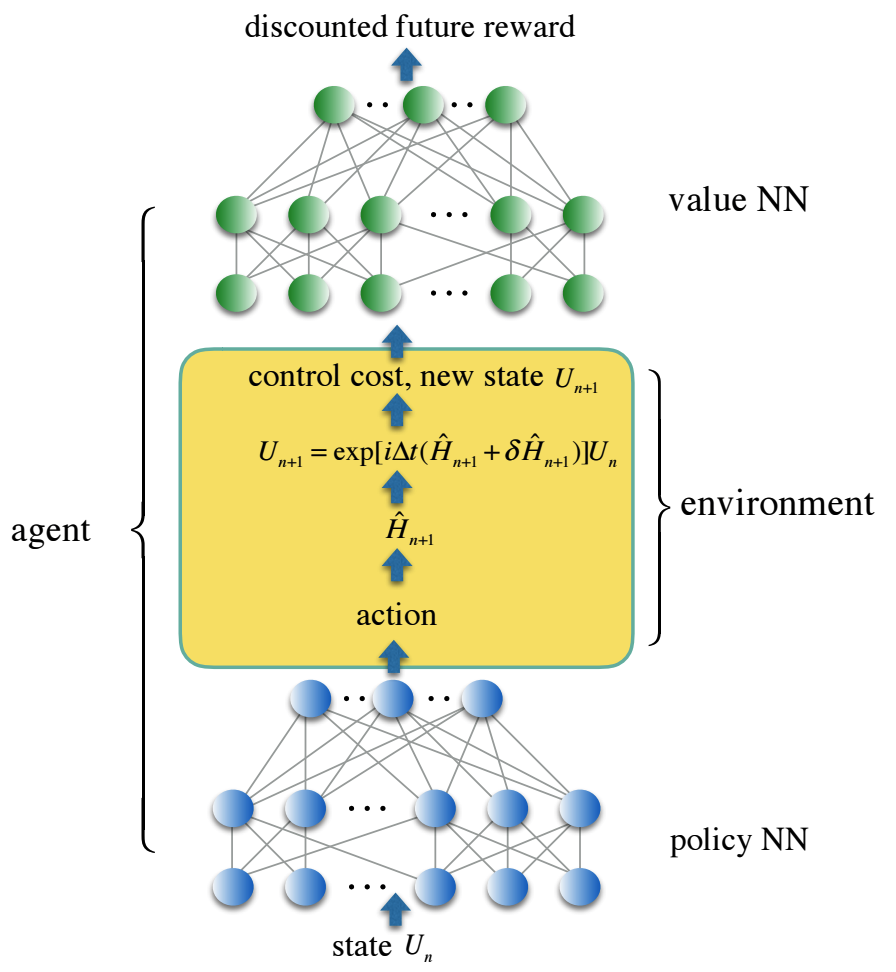
En el marco de esta nueva estructura, nuestra simulación numérica muestra una disminución de cien veces en los errores de las puertas cuánticas y una reducción en el tiempo de las puertas para la familia de puertas cuánticas de simulación continuamente parametrizadas en un promedio de un orden de magnitud en comparación con los enfoques tradicionales que utilizan un conjunto universal de puertas.
Este trabajo enfatiza la importancia de utilizar nuevos métodos de aprendizaje automático y los últimos algoritmos cuánticos que utilizan la flexibilidad y el poder de procesamiento adicional de un circuito de control cuántico universal. Para integrar completamente el aprendizaje automático y aumentar las capacidades computacionales, es necesario realizar experimentos adicionales, similares a los que se dieron en este trabajo.