Dos obras monumentales convencieron a muchos matemáticos de abandonar el signo igual. Su objetivo es reconstruir los fundamentos de la disciplina con la ayuda de una relación más débil: "equivalencia". Y este proceso no siempre funciona sin problemas.
El signo igual es la piedra angular de las matemáticas. Parece hacer una declaración fundamental y consistente: estas dos entidades son exactamente iguales.
Sin embargo, el círculo de matemáticos está creciendo, refiriéndose al signo igual, como al error inicial de las matemáticas. Consideran que es un brillo externo, que oculta las complejidades importantes de la relación entre cantidades, complejidades que pueden abrir soluciones a una gran cantidad de problemas. Quieren reformar las matemáticas usando un lenguaje de equivalencia más flexible.
"Generamos esta idea de igualdad", dijo
Jonathan Campbell, de la Universidad de Duke. "Y debería haber habido equivalencia en su lugar".
La figura más prominente en esta comunidad es
Jacob Lurie . En julio,
Lurie , de 41 años, renunció como empleada a tiempo completo en Harvard para un puesto de facultad en el Instituto Princeton de Estudios Avanzados, donde trabajaban algunos de los matemáticos más destacados del mundo.
Ideas de una escala como la de Lurie rara vez se encuentran en ningún campo. En sus libros de miles de páginas llenas de detalles técnicos, creó una forma sorprendentemente diferente de la forma habitual de comprender los conceptos más básicos de las matemáticas, yendo más allá del signo igual. "Creo que le pareció que esta era la forma correcta de pensar sobre las matemáticas", dijo
Michael Hopkins , matemático de Harvard y director de la escuela de posgrado.
Publicó su primer libro, The
Theory of Higher Topos , en 2009. Un volumen de 944 páginas sirve como una instrucción para interpretar áreas reconocidas de las matemáticas en el nuevo lenguaje de "categorías del infinito". En años posteriores, las ideas de Lurie penetraron en una amplia gama de disciplinas matemáticas. Muchos matemáticos los consideran indispensables para el futuro de este campo. "Nadie será el mismo después de estudiar las categorías de infinito", dijo
John Francis de la Universidad Northwestern,
Jacob LurieSin embargo, la difusión de las categorías de infinito reveló todos los problemas que atraviesa un respetado campo de las matemáticas, tratando de absorber nuevas ideas audaces, especialmente una idea que desafía su concepto más importante. "Hay un cierto nivel de conservadurismo en la comunidad matemática", dijo
Clark Barwick, de la Universidad de Edimburgo. "No creo que se pueda esperar que ningún grupo de matemáticos acepte rápidamente ninguna herramienta sin razones convincentes".
Aunque muchos matemáticos han aceptado las categorías del infinito, pocos han leído los textos largos y extremadamente abstractos de Lurie. Como resultado, parte del trabajo basado en sus ideas resulta ser menos riguroso de lo que se acepta en matemáticas.
"Escuché a la gente decir: 'Lurie lo tiene en alguna parte'", dijo
Inna Zakharevich , matemática de la Universidad de Cornell. - Y yo digo: '¿En serio? Se refiere a 8,000 páginas de texto '. Esto no es una referencia, es una apelación a la autoridad ".
Los matemáticos todavía están tratando de darse cuenta tanto de la amplitud de las ideas de Lurie como de la forma única de presentarlas. Extraen la esencia de su presentación de las categorías de infinito y la presentan en un nuevo paquete para que más matemáticos puedan usarla. En cierto sentido, llevan a cabo el liderazgo necesario, que está obligado a seguir cualquier revolución, traduciendo el texto revolucionario al código de leyes cotidiano. Por lo tanto, crean el futuro de los matemáticos, basados no en la igualdad, sino en la equivalencia.
Torres de equivalencia sin fin
La igualdad matemática parece la menos controvertida de todas las ideas. Dos cuentas más una cuenta equivalen a tres cuentas. ¿De qué más hay que hablar? Sin embargo, las ideas más simples pueden ser las más engañosas.
Desde finales del siglo XIX, los fundamentos de las matemáticas se han construido sobre conjuntos de objetos llamados conjuntos. La teoría de conjuntos establece las reglas, o axioma, para la creación y el manejo de estos conjuntos. Uno de estos axiomas, por ejemplo, afirma que puede agregar un conjunto de un elemento a un conjunto de dos elementos y obtener un nuevo conjunto de tres elementos: 2 + 1 = 3.
La forma formal de demostrar la igualdad de dos cantidades es unir pares entre sí. Haga coincidir una cuenta a la derecha del signo igual con una cuenta a la izquierda. Después de todas las comparaciones, no quedarán cuentas adicionales.
La teoría de conjuntos reconoce que dos conjuntos de tres objetos cada uno se pueden combinar con precisión entre sí, pero no significa todas las diferentes formas posibles de tal comparación. La primera cuenta de la derecha puede recoger un par en la forma de la primera cuenta de la izquierda, o hacer coincidir el primero de la derecha con el segundo de la izquierda, y así sucesivamente (puede haber seis de esos pares). Decir que dos más uno es igual a tres, y terminar con esto significa no ver todas las formas posibles de igualarlos. "El problema es que hay muchas maneras de emparejar", dice Campbell. "Y los olvidamos cuando decimos iguales".
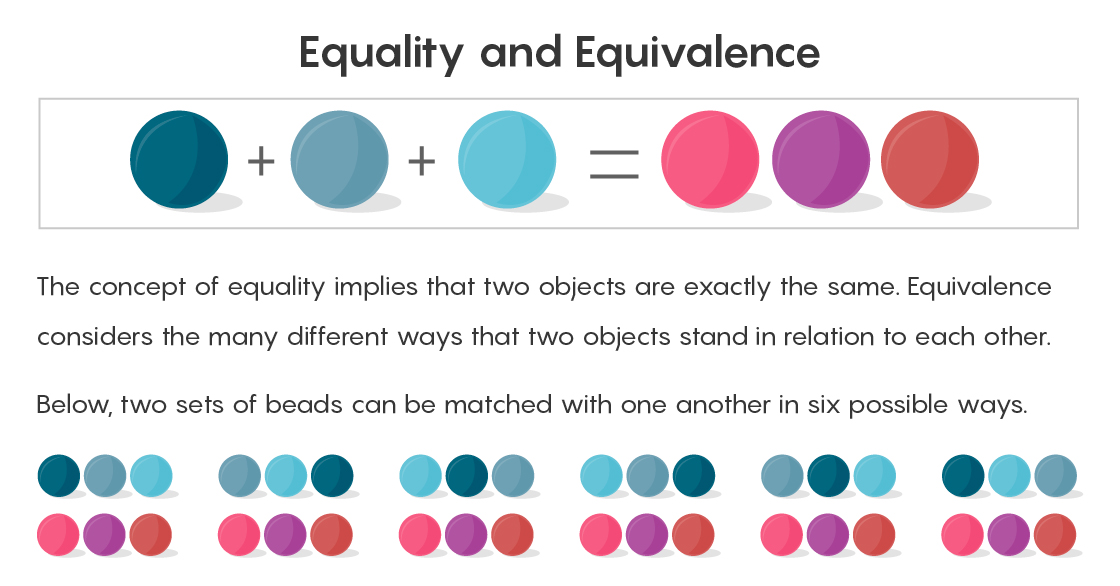
Aquí es donde entra en juego la equivalencia. Si la igualdad es una relación clara, dos cosas son iguales o no, la equivalencia puede ser diferente.
Cuando emparejas con precisión cada elemento de un conjunto con cada elemento de otro, obtienes una fuerte equivalencia. Pero, por ejemplo, en un campo de las matemáticas como la
homotopía , dos formas (o figuras geométricas) son equivalentes si una se puede transformar en otra al estirarla o comprimirla sin romperla.
Desde el punto de vista de la teoría de la homotopía, un disco plano y un punto en el espacio son equivalentes: el disco se puede comprimir a un punto. Sin embargo, no puede hacer coincidir los puntos en un disco con los puntos en un punto. De hecho, el disco de puntos tiene un número infinito, y un punto es solo un punto.
Desde mediados del siglo XX, los matemáticos han estado tratando de desarrollar una alternativa para establecer la teoría en la que las matemáticas serían más fáciles de tratar en términos de equivalencia. En 1945, los matemáticos
Samuel Eileberg y
Saunders MacLane introdujeron un nuevo objeto fundamental con equivalencia incorporada. Lo llamaron una categoría.
Una categoría puede llenarse con cualquier cosa. Puede tomar la categoría de mamíferos, que incluirá todas las criaturas peludas de sangre caliente que producen leche. O puede crear categorías de objetos matemáticos: conjuntos, formas geométricas o sistemas numéricos.
Una categoría es un conjunto con metadatos adicionales: una descripción de todas las formas de hacer coincidir un objeto con otro, que incluye una descripción de todas las características por las cuales dos objetos pueden considerarse equivalentes. Las categorías también se pueden imaginar como objetos geométricos en los que cada elemento de la categoría está representado por un punto.
Imagine, por ejemplo, la superficie de una pelota. Cada punto en esta superficie puede indicar su tipo de triángulos. Las rutas entre puntos expresan una relación de equivalencia entre objetos. Desde el punto de vista de la teoría de categorías, olvidamos la forma específica de describir un objeto y, en cambio, nos concentramos en el lugar que ocupa el objeto en relación con todos los demás objetos de este tipo.
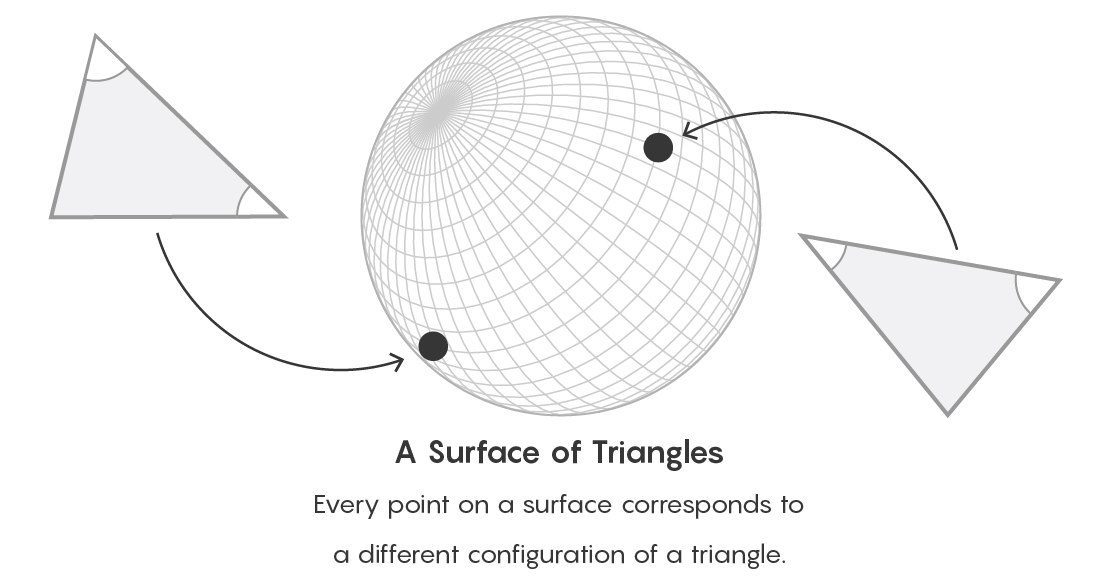Cada punto en la superficie corresponde a un tipo particular de triángulos."Tratamos muchas cosas como cosas, aunque en realidad son una relación entre las cosas", dijo Zakharevich. - La frase "mi esposo" significa algo que consideramos un objeto, pero se puede considerar como una relación. Una cierta parte está determinada por la relación conmigo.
La versión de categoría de Eilenberg y MacLane era adecuada para trabajar con opciones de equivalencia sólidas. Pero en la segunda mitad del siglo XX, los matemáticos utilizaron cada vez más formas de equivalencia más débiles, como la homotopía. "Las matemáticas se están volviendo más sutiles e inevitablemente deseamos ideas más sutiles sobre las cosas comunes", dijo Emily Riel, matemática de la Universidad Johns Hopkins. En estas versiones más finas de equivalencia, la cantidad de información sobre la relación entre dos objetos aumenta bruscamente. Las categorías rudimentarias de Eilenberg y MacLane no estaban destinadas a esto.
Para ver un aumento en la cantidad de información, primero recuerde nuestra esfera, que denota diferentes triángulos. Dos triángulos son homotópicamente equivalentes si uno puede transformarse en otro por estiramiento u otra deformación. Dos puntos en una superficie son homotópicamente equivalentes si hay una ruta que los conecta. Al estudiar caminos homotópicos entre puntos en una superficie, en realidad estás estudiando las diferentes formas en que los triángulos denotados por estos puntos están conectados entre sí.
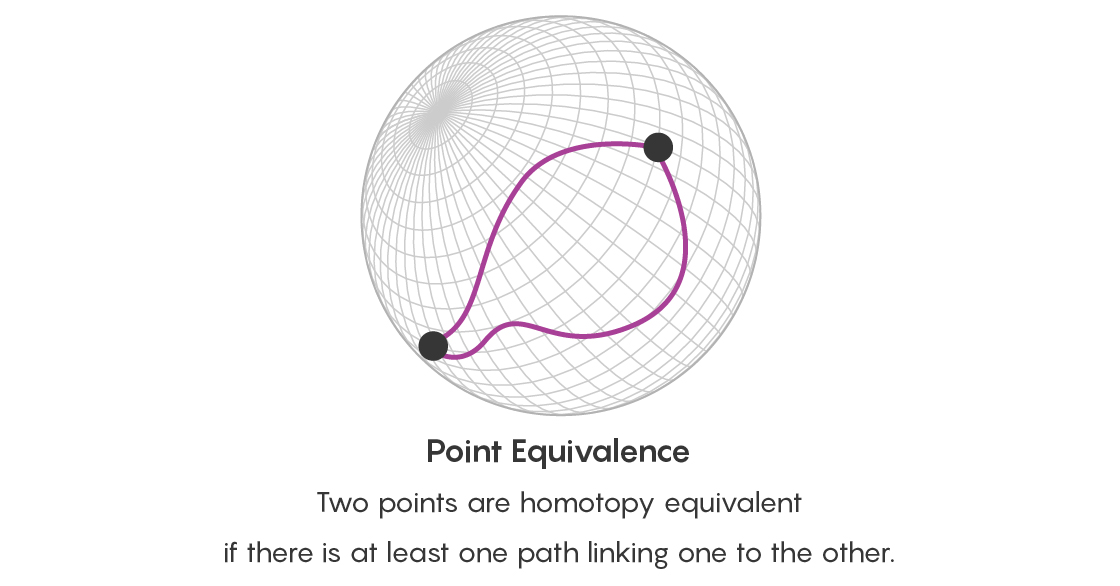
Sin embargo, no es suficiente afirmar que dos puntos están conectados de muchas maneras equivalentes. También es necesario pensar en la equivalencia de todos estos caminos. Por lo tanto, además de la cuestión de equivalencia de puntos, ahora hace la pregunta de equivalencia de dos caminos que comienzan y terminan en los mismos puntos, y ¿hay un camino que conecte estos caminos? Esta ruta que conecta las rutas toma la forma de un disco, cuyo límite son dos de estas rutas.
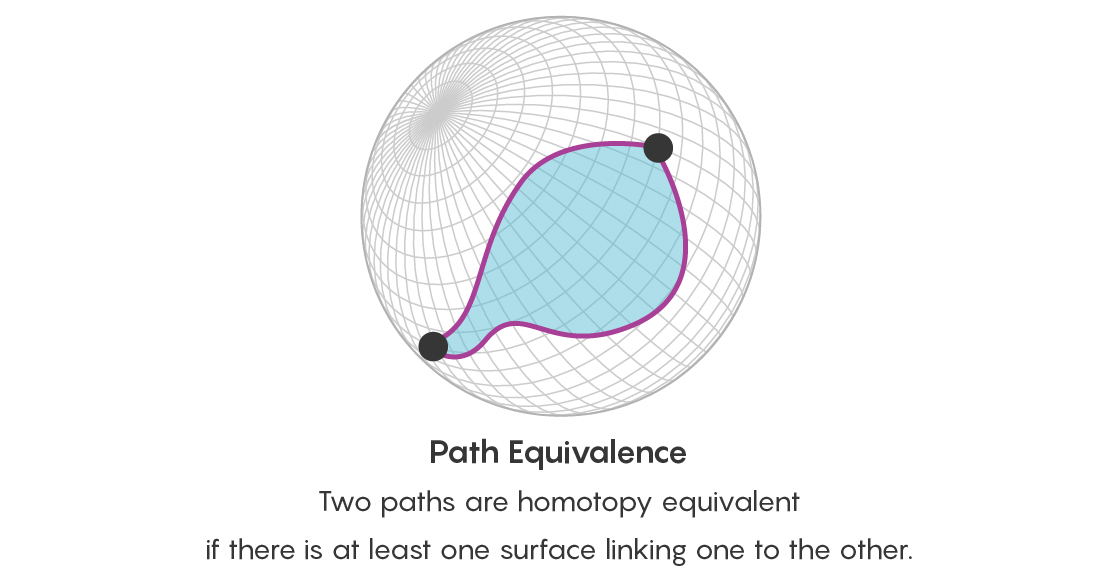
Puedes desarrollar esta idea aún más. Dos discos son equivalentes si están conectados por una ruta, y esta ruta tomará la forma de un objeto tridimensional. Dichos objetos tridimensionales pueden conectarse por sí mismos mediante caminos de cuatro dimensiones (el camino entre dos objetos siempre tiene una dimensión más que los objetos mismos).
Como resultado, construyes una torre interminable de equivalencia entre equivalencias. Discutiendo sobre toda la doctrina, genera una vista general de todos los objetos que ha marcado con puntos en la esfera.
"Es solo una esfera, pero resulta que para comprender la forma de una esfera, debes ir al infinito de alguna manera", dijo
David Ben-Zvi de la Universidad de Texas en Austin.
En las últimas décadas del siglo XX, muchos matemáticos han trabajado en la teoría de las "categorías de infinitos", en lo que es capaz de rastrear una torre infinita de equivalencias entre equivalencias. Algunos de ellos han logrado serios éxitos. Pero solo uno llegó al final.
Reescribiendo Matemáticas
El primer trabajo de Jacob Lurie en las categorías de infinito no tuvo mucho éxito. El 5 de junio de 2003, el científico de 25 años publicó un documento de 60 páginas titulado "
Sobre el Topos del Infinito " en el sitio de preimpresiones científicas arxiv.org. Allí comenzó a hacer borradores de las reglas por las cuales los matemáticos podían trabajar con categorías de infinito.
No todos aceptaron el primer trabajo de la misma manera. Poco después de leer,
Peter May , matemático de la Universidad de Chicago, escribió al supervisor de Lurie, Michael Hopkins, que aunque el trabajo de Lurie contiene ideas interesantes, parece inacabado y requiere un enfoque más disciplinado.
"Le expliqué nuestros comentarios a Mike y él se los pasó a Jacob", dijo May.
No se sabe si Lurie tomó la carta de May como un desafío, o si ya había planeado su próximo paso (Lurie rechazó numerosas solicitudes de entrevista). Está claro que después de recibir comentarios críticos, Lurie golpeó en un período de productividad de varios años, que más tarde se convirtió en legendario.
"No puedo entrar en el cerebro de Jacob y, por lo tanto, no sé exactamente qué estaba pensando en ese momento", dijo May. "Pero hay una gran diferencia entre el borrador que revisamos y las versiones finales, que ya están en un nivel matemático completamente diferente".
En 2006, Lurie publicó en arxiv.org un borrador de "Theories of Highest Topos". En este trabajo monumental, creó el aparato necesario para reemplazar la teoría de conjuntos con una nueva base para las matemáticas basada en las categorías del infinito. "Creó literalmente miles de páginas de este aparato fundamental que todos usamos ahora", dijo Charles Rezk, matemático de la Universidad de Illinois en Urbana-Champaign, quien realizó un trabajo importante desde el principio en el desarrollo de categorías infinitas. "No puedo imaginar cómo es posible crear una obra como 'Theory of the Highest Topos' en una vida, y la creó en dos o tres años".
Luego, en 2011, Lurie dio otro trabajo, incluso más largo. En él, reinventó el álgebra.
El álgebra nos da un maravilloso conjunto de reglas formales para manipular ecuaciones. Los matemáticos usan constantemente estas reglas para probar teoremas. Sin embargo, el álgebra hace gimnasia en las barras fijas del signo igual. Elimine estas barras, reemplazándolas con un concepto más efímero de equivalencia, y algunas operaciones se volverán muy complicadas.
Tome una de las primeras reglas de álgebra que los niños aprenden en la escuela: la asociatividad. La suma o producto de tres o más números no depende de su agrupación: 2 × (3 × 4) = (2 × 3) × 4.
Es fácil probar la propiedad de asociatividad para una lista de tres o más números si trabaja con igualdad. Esto es difícil cuando trabajas incluso con el concepto de equivalencia fuerte. Pero cuando pasas a versiones más sutiles de equivalencia, con sus torres interminables de caminos que conectan los caminos, incluso una regla simple, similar a la asociatividad, se convierte en un bosque oscuro.
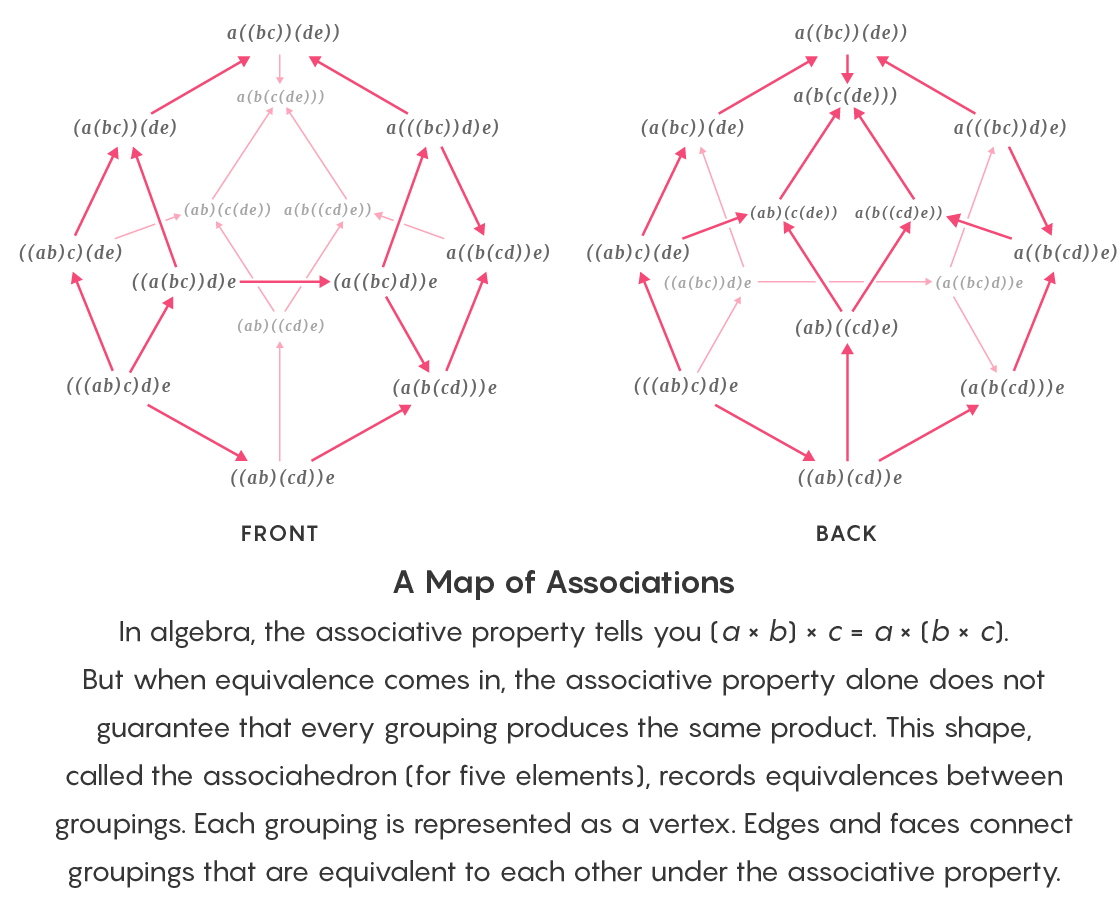En álgebra, la asociatividad establece que (a × b) × c = a × (b × c). Pero con el uso de equivalencia, la asociatividad por sí sola no garantiza que cualquier agrupación de elementos produzca el mismo resultado de multiplicación. Este assocaedro contiene registros de equivalencia grupal. Cada vértice corresponde a una agrupación. Los bordes y las caras combinan grupos asociativamente equivalentes entre sí."Esto hace que el problema sea extremadamente complicado, lo que hace que sea imposible trabajar con esta nueva versión de las matemáticas", dijo David Isla, matemático de la Universidad de Montana.
En Álgebra superior, cuya última versión abarca más de 1553 páginas, Lurie desarrolló una opción de asociatividad para categorías infinitas, así como muchos otros teoremas algebraicos que juntos forman la base de las matemáticas de las equivalencias.
Estos dos libros produjeron el efecto de una bomba explosiva; tales trabajos dan lugar a una revolución científica. "La escala fue extraordinaria", dijo Reel. "Fue el logro del nivel de
Grothendieck en geometría algebraica".
Sin embargo, la revolución lleva tiempo y, como descubrieron los matemáticos después de la publicación de los libros de Lurie, estos años pueden ser caóticos.
Digiere una vaca
Los matemáticos son considerados personas con un pensamiento inequívoco: la prueba es cierta o no; La idea funciona o no. Sin embargo, los matemáticos también son personas comunes, y reaccionan a las nuevas ideas de la misma manera que las personas comunes: subjetiva, emocional, con motivos personales.
"Creo que se han escrito muchos textos sobre matemáticos en tal tono que están buscando una verdad clara y cristalina", dijo Campbell. "Pero esto no está sucediendo". Estas son personas con sus propios gustos, zonas de confort y pueden negar cosas que no les gustan por razones estéticas o personales ".
En este sentido, el trabajo de Lurie se ha convertido en un desafío complejo para la comunidad. De hecho, fue provocativo: aquí hay una nueva y mejor manera de hacer matemáticas. Este mensaje fue dirigido especialmente a los matemáticos, quienes pasaron toda su carrera desarrollando métodos que Lurie destacó.
"A la gente no siempre le gusta ver a la próxima generación reescribir su trabajo, y este proceso genera estrés", dijo Francis. "Esta es una de las características de la teoría de las categorías del infinito: la mayoría de los trabajos anteriores corresponden".
El trabajo de Lurie fue difícil de digerir por otros motivos. El volumen de materiales significaba que los matemáticos tendrían que pasar años leyendo sus libros. Es casi imposible exigir a los matemáticos ocupados que están en la mitad de una carrera, y para los estudiantes graduados que tienen solo unos pocos años para dar un resultado que les permita encontrar un trabajo, esto es muy riesgoso.
El trabajo de Lurie también fue muy abstracto, incluso en comparación con la naturaleza extremadamente abstracta de todo lo avanzado en estudios de matemáticas. Y no a todos les gustó. "Mucha gente pensó que el trabajo de Lurie era basura abstracta, y muchos simplemente se enamoraron de ella", dijo Campbell. "Había opciones intermedias, incluidas las que no la entendían en absoluto".
Carrete EmilyLa comunidad científica percibe constantemente nuevas ideas, pero generalmente esto sucede lentamente y con la sensación de que todos se están moviendo al mismo tiempo. El surgimiento de nuevas ideas crea dificultades para el aparato intelectual de la comunidad. "Muchas cosas nuevas surgen de inmediato, es como una boa tratando de digerir una vaca", dijo Campbell. "Una gran masa pasa por la comunidad".
Si usted es un matemático que cree que el enfoque de Lurie es la mejor manera de hacer matemáticas, entonces su camino hacia adelante será solitario. Pocas personas leen el trabajo de Lurie, no había libros de texto para contarlos brevemente, ni seminarios para ayudarlo a orientarse. "Solo había una forma de estudiar todo esto con gran detalle: sentarse y hacer todo usted mismo", dijo Peter Heine, un estudiante graduado en el MIT que pasó un año leyendo el trabajo de Lurie. - Creo que esto es lo más difícil. "No es fácil sentarse y descubrirlo usted mismo, es decir, sentarse y leer 800 páginas de Theory of the Topos Theory.
Al igual que muchos inventos nuevos, la teoría de los topos superiores requiere que los matemáticos interactúen activamente con el aparato, lo que le permite funcionar.
Así es como hacer que cada niño de 16 años que sueña con una licencia de conducir aprenda primero cómo resolver el motor. "Si hubiera una versión más amigable de todo esto, entonces la teoría sería inmediatamente más accesible para círculos matemáticos más amplios", dijo Dennis Gatesgory, un matemático de Harvard que trabajó con Lurie.Cuando la gente comenzó a leer el trabajo de Lurie y usar las categorías de infinito en sus estudios, aparecieron otros problemas. Los matemáticos construyeron su trabajo sobre la base de las categorías del infinito. Los revisores de revistas recibieron estos documentos y preguntaron: ¿qué es?"Hubo una situación en la que el trabajo regresaba de revistas con críticas absurdas, de las cuales se veía una falta total de comprensión, o tardó varios años en publicarlas", dijo Barvik. "Puede ser un gran inconveniente, porque el trabajo inédito que ha estado en su sitio durante años parece cada vez más ridículo".Sin embargo, el mayor problema no fueron los trabajos inéditos, sino los trabajos que utilizan las categorías de infinito y publicados, pero que contienen errores.Los libros de Lurie son la única fuente autorizada de información sobre las categorías del infinito. Son estrictos, pero es difícil entenderlos completamente. Y son especialmente inadecuados para el papel de las instrucciones a las que se podría hacer referencia: es difícil buscar ciertos teoremas o verificar que una determinada aplicación de las categorías de infinito encontradas en el trabajo de alguien realmente funcione."La mayoría de los matemáticos que trabajan en este campo no leyeron a Lurie sistemáticamente", dijo Andre Joyal, matemático de la Universidad de Quebec en Montreal, cuyo trabajo inicial fue un ingrediente clave en los libros de Lurie. “Se necesita mucho tiempo y energía, por lo que asumimos que todo lo que está escrito en sus libros es verdadero, porque casi cada vez que revisamos algo, resulta ser cierto. De hecho, cada vez ".La inaccesibilidad de los libros de Lurie condujo a imprecisiones en algunos de los estudios que siguieron. Los libros de Lurie son difíciles de leer, difíciles de citar y difíciles de usar para evaluar el trabajo de otras personas."La literatura general sobre el tema de las categorías del infinito parece desordenada", dijo Zakharevich.A pesar de todo su formalismo, las matemáticas no deberían ser un texto sagrado que solo los sacerdotes puedan leer. En esta área no solo se requieren grandes volúmenes, sino también folletos, no solo las revelaciones iniciales, sino también las interpretaciones de sus descripciones. Mientras tanto, la teoría de las categorías infinitas existe, en su mayor parte, en forma de varios libros grandes en un estante."Puedes tomar el enfoque. 'Jacob te dirá qué hacer, y todo está en orden", dijo Rezk. "O puede decidir que" No sabemos cómo presentar nuestro tema lo suficientemente bien como para que las personas puedan usarlo ".Sin embargo, pocos matemáticos pudieron aceptar el desafío y hacer de la categoría de infinito una tecnología que podrían usar más personas de su campo de estudio.Teoría de uso fácil
Para traducir las categorías de infinitos en un objeto capaz de trabajo matemático real, Lurie tuvo que probar los teoremas asociados con ellos. Y para esto, tuvo que elegir un paisaje en el que crear esta evidencia; al igual que una persona que se dedica a la geometría, es necesario elegir un sistema de coordenadas para el trabajo. Los matemáticos llaman a este modelo de selección.Lurie desarrolló las categorías de infinitos en el modelo de cuasicategorías. Otros matemáticos antes que él desarrollaron las categorías de infinitos en otros modelos. Y aunque su trabajo no fue tan completo como el de Lurie, en algunas situaciones es más fácil tratar con ellos. "Jacob eligió un modelo y comprobó que todo funciona en él, pero a menudo no es el más fácil", dijo Zakharevich.En geometría, los matemáticos entienden claramente cómo moverse entre diferentes sistemas de coordenadas. También demostraron que los teoremas demostraron que en algunas condiciones funcionan en otras.Para categorías infinitas, tales garantías no existen. Sin embargo, cuando los matemáticos escriben trabajos utilizando las categorías de infinitos, a menudo cambian fácilmente entre modelos, lo que sugiere (pero no prueba) la portabilidad de los resultados. "Las personas no especifican lo que están haciendo, cambian entre todos estos modelos diferentes y dicen: Ah, es lo mismo", dijo Heine. "Pero eso no es una prueba".En los últimos seis años, un par de matemáticos han intentado obtener estas garantías. Ryl y Dominic Verityde la Universidad de McUyra en Australia, desarrolló una forma de describir las categorías de infinitos, superando las dificultades que aparecían en plataformas anteriores usando ciertos modelos. Su trabajo, basado en los trabajos anteriores de Barvik y otros, demostró que muchos de los teoremas de la Teoría del Topos Superior siguen siendo ciertos independientemente del modelo utilizado. Y demuestran esta compatibilidad de manera apropiada: "Estudiamos las categorías del infinito, cuyos objetos son las categorías del infinito", dijo Ril. "La teoría de la categoría muerde su cola".Ril y Verity esperan desarrollar la teoría de las categorías de infinitos de otra manera. Eligen aspectos de la teoría que funcionan independientemente del modelo. Dicha presentación, independiente del modelo, tiene una calidad conveniente de aplicabilidad instantánea, que, esperan, atraerá a los matemáticos a esta área de investigación que se mantuvieron alejados cuando la única entrada fue The Higher Topos Theory."Para entrar en este mundo, necesitas superar el foso", dijo Hopkins. "Y lo hacen bajar el puente".Ryl y Verity planean terminar el trabajo el próximo año. Mientras tanto, Lurie recientemente comenzó a trabajar en el proyecto Kerodon., que planeaba convertir en una especie de libro de referencia sobre la teoría de la categoría más alta, similar a Wikipedia. Trece años después de que la Teoría de Topos formalizara las matemáticas de la equivalencia, estas iniciativas intentan refinar y difundir estas ideas, a fin de hacer que las matemáticas de la equivalencia sean más accesibles."El genio tiene un papel importante en el desarrollo de las matemáticas, pero el conocimiento en sí mismo es el resultado del trabajo de toda la comunidad", dijo Zhoyal. "El objetivo real del conocimiento es convertirse en conocimiento de toda la comunidad y no pertenecer a una o dos personas".