Siguiendo los pasos de
"Our won: TopCoder Open 2019" publico tareas de la pista Algorithm
(programación deportiva clásica. En una hora y media, debe resolver tres problemas en Java, C #, C ++ o Python).1. Pie para seis
Declaración del problema.El límite de tiempo es de 4 segundos.
Tienes un pastel Visto desde arriba, el pastel tiene la forma de un polígono convexo (estrictamente). Te dan las coordenadas de los vértices en los enteros X e Y.
Tienes cinco amigos Desea dividir el pastel en seis piezas de igual área (pero no necesariamente la misma forma). Por supuesto, cualquiera puede hacerlo en cinco cortes, pero solo los profesionales pueden hacerlo en tres cortes.
Encuentra tres cortes en línea recta a través de un punto que divida el pastel en seis piezas del mismo tamaño. Imprima {x, y, d1, d2, d3}, donde (x, y) es el punto común de las tres secciones, y d1, d2, d3 son los ángulos de dirección de las secciones en radianes.
DefiniciónClase: CakeForSix
Método: corte
Parámetros: int [], int []
Devoluciones: doble []
Firma del método: corte doble [] (int [] x, int [] y)
(asegúrese de que su método sea público)
Notas- La dirección positiva a lo largo del eje x es 0 (radianes), la dirección positiva a lo largo del eje y es pi / 2 (radianes).
- El corte en la dirección d es similar al corte en la dirección pi * k + d para cualquier número entero k.
- Puede generar cualquier dirección, no tienen que ser de [0, pi).
- El calificador calculará el área de sus seis pedazos de pastel en dobles. La respuesta será aceptada si la diferencia relativa o absoluta entre ellos es menor que 10 ^ (- 4).
- Más precisamente, deje que X e Y sean las más pequeñas y más grandes de sus seis áreas calculadas por el calificador. Entonces su respuesta será aceptada si Y <max (X + 10 ^ (- 4), X * 1 + 10 ^ (- 4))).
- (En la versión original del problema, se usó la precisión 1e-7 en lugar de 1e-4. Para resolver este problema en el archivo, el límite de precisión se redujo debido a la presencia de casos de llamadas que probablemente hacen que la tarea no pueda resolverse con precisión 1e-7. En un mundo ideal, restricciones no permita tales casos y aún requiera una alta precisión, por lo que resolver el problema con alguna optimización numérica general no es fácil).
Limitaciones- x contiene de 3 a 50 elementos inclusive.
- y contiene tantos elementos como x.
- todas las coordenadas entre 0 y 10,000 inclusive
- x e y definen un polígono convexo en sentido antihorario.
Original en inglesDeclaración del problema
El límite de tiempo es de 4 segundos.
Tienes un pastel Visto desde arriba, el pastel es un polígono convexo (estrictamente). Se le dan las coordenadas de sus vértices en int [] sx e y.
Tienes cinco amigos Ahora desea cortar el pastel en seis piezas de igual área (pero no necesariamente de igual forma). Por supuesto, cualquiera puede hacer eso en cinco cortes, ¡pero solo un verdadero profesional puede hacerlo en tres!
Encuentra tres cortes en línea recta que pasen por el mismo punto que cortó el pastel en seis partes igualmente grandes. Devuelve {x, y, d1, d2, d3}, donde (x, y) es el punto común de los tres cortes, y d1, d2, d3 son sus direcciones en radianes.
Definición
Clase: CakeForSix
Método: corte
Parámetros: int [], int []
Devoluciones: doble []
Firma del método: corte doble [] (int [] x, int [] y)
(asegúrese de que su método sea público)
Notas
- La dirección positiva a lo largo del eje x es 0 (radianes), la dirección positiva a lo largo del eje y es pi / 2 (radianes).
- Un corte en la dirección d es lo mismo que un corte en la dirección pi * k + d para cualquier número entero k.
- Puede devolver cualquier dirección, no tienen que ser de [0, pi).
- El calificador calculará las áreas de sus seis pedazos de pastel en dobles. La respuesta será aceptada si la diferencia relativa o absoluta entre ellos es menor que 10 ^ (- 4).
- Más precisamente, deje que X e Y sean las más pequeñas y más grandes de sus seis áreas, según lo calculó el calificador. Entonces, su respuesta será aceptada si Y <max (X + 10 ^ (- 4), X * (1 + 10 ^ (- 4))).
- (La versión original del problema usaba precisión 1e-7 en lugar de 1e-4. Para resolver este problema en el archivo, el límite de precisión se redujo debido a la existencia de casos de desafío que muy probablemente hacen que la tarea no pueda resolverse con precisión 1e-7 En un mundo ideal, las restricciones no permitirían tales casos y aún requieren una alta precisión, por lo que no es fácil resolver el problema mediante una optimización numérica general).
Restricciones
- x tendrá entre 3 y 50 elementos, inclusive.
- y tendrá el mismo número de elementos que x.
- Todas las coordenadas estarán entre 0 y 10,000, inclusive.
- x e y describirán un polígono convexo en el sentido contrario a las agujas del reloj.
Ejemplos
0){0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Devoluciones:
{24.999999999437453, 9.999999999500002, 0.0, 0.7266423406817211, 2.4149503129080787}
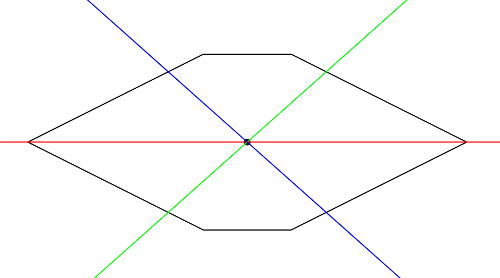
Hexágono simétrico pero no regular. Un ejemplo de una respuesta corresponde a cortarlo por la mitad horizontalmente y hacer otros dos cortes en el centro, que dividen cada parte en tres partes.
 1)
1){0, 1000, 0}
{0, 0, 1000}
Devoluciones:
{333.3333333331763, 333.3333333332546, 0.7853981633986264, 2.0344439357948154, 2.6779450445891753}
Triángulo rectángulo Nuevamente, podemos comenzar con uno de los tres cortes a lo largo del eje de simetría.
 2)
2){40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Devoluciones:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475}
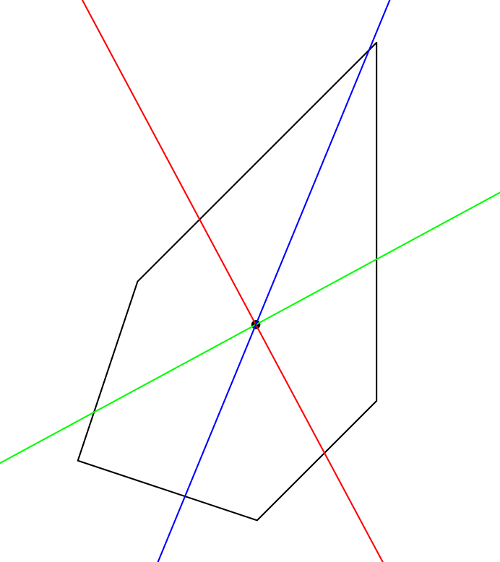
Pentágono equivocado.
 3)
3){300, 400, 300, 200}
{500, 600, 700, 600}
Devoluciones: {299.99999999974995, 599.9999999995, 0.0, 1.107148717794088, 2.034443935795705}
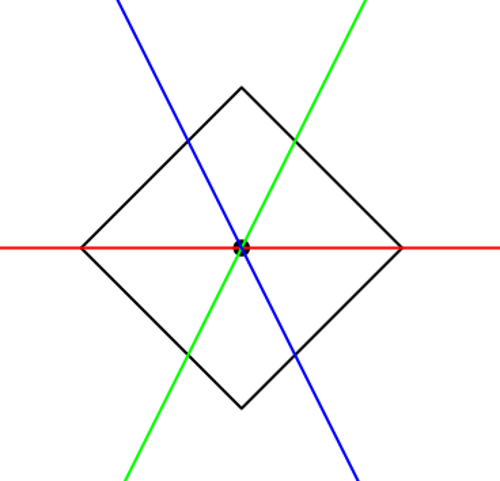
Un cuadrado rotado 45 grados.
[
Fuente ]