Buenas tardes Escribí este artículo especialmente para los estudiantes del curso "Algorithms for Developers" en OTUS y hoy quiero compartirlo con todos los lectores de nuestro blog.Un caballo de ajedrez se para en un tablero de ajedrez y mira cuidadosamente el tablero de ajedrez.
¿Cuántos movimientos diferentes puede hacer?

Alabado sea el inventor del ajedrez, hay
64 celdas en el tablero.
Elogio al arquitecto informático: el tipo
ulong también tiene
64 bits.
Esta coincidencia tuvo que suceder!
La idea brillante se sugiere a sí misma: ¡almacenar
todo el tablero en
un número entero ! Incluso hay un término especial para esta solución:
Bitboard , una placa de bits.
Entonces, ¿cómo encontrar
rápidamente el número de movimientos de un caballo de ajedrez usando esta idea?
Dado:
knightNr - número de celda del tablero donde está el caballo (de 0 a 63).
Es necesario:
movesCount : el número de campos donde puede ir (de 2 a 8).
Algoritmo
1. Convertir el número de la jaula del caballo a
ulong - valor del tablero de bits
knightNr ->
knightBits2. Establecer bits para todos los movimientos posibles del caballo
knightBits ->
movesBits3.Cuenta el número de bits unitarios
movesBits ->
movesCount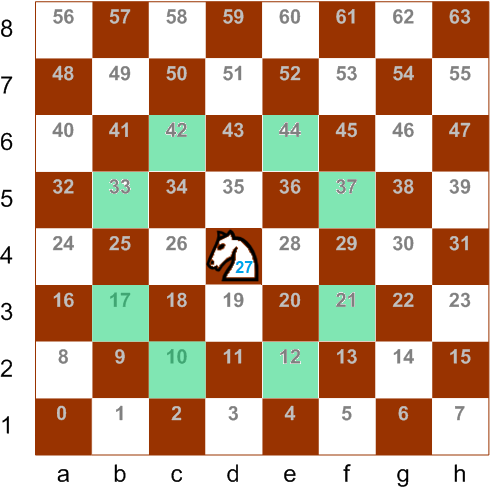
El primer paso es muy simple, debe desplazar el bit cero a la izquierda por el número especificado de posiciones.
ulong knightBits = 1 << knightNr;
El segundo paso es un poco más complicado. Un caballo puede ir en 8 direcciones diferentes. Consideraremos estos desplazamientos no "horizontal / verticalmente", sino por posiciones de bit. Es decir, consideramos cuántas posiciones necesita para cambiar el bit de inicio de cada movimiento. Luego "sumamos" todo con una operación lógica "o".
Comencemos enumerando los movimientos desde el lado izquierdo del tablero hacia la derecha:
movesBits = knightBits << 6 | knightBits >> 10
Es cierto, genial!
Desafortunadamente, hay "agujeros negros" en los bordes del tablero. Por ejemplo, de acuerdo con este algoritmo, desde la celda a4 (bit # 24) puede llegar a la celda g2 (bit # 14 = 24-10), este salto es una
teletransportación de un caballo de ajedrez esférico en el vacío en un tablero a través de un agujero negro a las verticales extremas ...
Para excluir el salto cuántico del caballo sobre el borde del tablero, es necesario "desconectar" las bandas extremas después de moverse. Por ejemplo, para los movimientos +6 y -10 (dos celdas a la izquierda), es necesario cancelar los valores obtenidos en las verticales g y h, ya que no puede terminar en estas verticales después de moverse "a la izquierda" para dos movimientos.
Para hacer esto, necesitamos constantes de cuadrícula de 4 bits, en las que todos los bits se establecen en 1, excepto las verticales indicadas. A saber:
ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f;
En la parte superior e inferior del tablero de ajedrez también hay "agujeros negros" que absorben completamente al caballo, por lo que no es necesario revisarlos por separado.
Ahora el algoritmo para generar movimientos de caballos permitidos se ve así:
movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6);
Funciona muy (!) Rápido.
Unos pocos ticks, y tenemos un mapa de bits de todas las posibles aventuras de caballos. Lo más sorprendente es que este algoritmo funciona bien incluso si hay varios caballos en el tablero. ¡Inmediatamente genera todos los movimientos posibles para todos los caballos! Es cierto, genial!
Queda por contar el número de bits.
La forma más fácil es desplazar el número 1 bit hacia la derecha y contar los unos. Dificultad - 64 operaciones. Memoria - 64 bits.
La forma más rápida es crear un caché / matriz con 65536 elementos, en el que el número de bits para cada índice se escribe de 0 a 65535. Y agregue 4 elementos de esta matriz que correspondan a los siguientes segmentos de 16 bits del número.
Dificultad - 4 operaciones. Memoria - 64 kilobytes.
Pero consideraremos la forma
más complicada , cuya complejidad es igual al número de bits individuales en el número. Como no hay muchos movimientos, este enfoque será el más óptimo para nosotros.
Para empezar, notamos que restando una unidad de un número, convertimos todos los ceros "correctos" en unidades, y la unidad más externa en cero:
1001010100010000 - 1 = 1001010100001111
A continuación, aplique la operación lógica "y" para estos números:
1001010100010000 & 1001010100001111 = 1001010100000000
Como puede ver, de una manera tan complicada restablecemos la unidad de la derecha a cero. Repita esta operación hasta que obtengamos cero como resultado. Cuántas iteraciones, tantos bits individuales. Es cierto, genial!
Así es como se escribe este algoritmo en su totalidad:
int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; }
¡El problema está resuelto!
Esta tarea tiene otra solución muy simple y puramente lógica: determinar la distancia del caballero desde el borde del tablero de ajedrez (en la esquina hay 2 movimientos, cerca del borde de 3 a 6 movimientos, en el centro de 8 movimientos). Pero si resolviéramos el problema "de frente" de esta manera, no sabríamos sobre el tablero de bits, sobre las máscaras de bits verticales, sobre el algoritmo para contar rápidamente bits individuales y sobre los agujeros negros para caballos esféricos en el vacío ...
Ahora sabemos todo al respecto. La vida de un programador de ajedrez se ha vuelto más rica y significativa, ¡salud!
Tarea de bricolaje: haz lo mismo para el Rey del Ajedrez.