💇🏻 ✊🏼 👨🏾‍🏭 Optimización de estrategia de blackjack de Monte Carlo 👩🏿‍🚀 ↕️ ⏯️

La traducción del artículo fue preparada específicamente para estudiantes del curso de Machine Learning .

El entrenamiento reforzado tomó el mundo de la Inteligencia Artificial. A partir de AlphaGo y AlphaStar , un número cada vez mayor de actividades que antes eran dominadas por humanos ahora son conquistadas por agentes de IA basados en entrenamiento de refuerzo. En resumen, estos logros dependen de la optimización de las acciones del agente en un entorno particular para lograr la máxima recompensa. En los últimos artículos de GradientCrescent, hemos analizado varios aspectos fundamentales del aprendizaje reforzado, desde los conceptos básicos de los sistemas de bandidos y los enfoques basados en políticas hasta la optimización del comportamiento basado en recompensas en los entornos de Markov . Todos estos enfoques requieren un conocimiento completo de nuestro entorno. La programación dinámica , por ejemplo, requiere que tengamos una distribución de probabilidad completa de todas las posibles transiciones de estado. Sin embargo, en realidad, encontramos que la mayoría de los sistemas no se pueden interpretar completamente, y que las distribuciones de probabilidad no se pueden obtener explícitamente debido a la complejidad, la incertidumbre inherente o las limitaciones en las capacidades computacionales. Como analogía, considere la tarea del meteorólogo: la cantidad de factores involucrados en el pronóstico del tiempo puede ser tan grande que es imposible calcular con precisión la probabilidad.

Para tales casos, los métodos de enseñanza como Monte Carlo son la solución. El término Monte Carlo se usa comúnmente para describir cualquier enfoque para la estimación de muestreo aleatorio. En otras palabras, no predecimos el conocimiento sobre nuestro entorno, sino que aprendemos de la experiencia al pasar por secuencias ejemplares de estados, acciones y recompensas obtenidas como resultado de la interacción con el entorno. Estos métodos funcionan observando directamente las recompensas devueltas por el modelo durante la operación normal para juzgar el valor promedio de sus condiciones. Curiosamente, incluso sin ningún conocimiento de la dinámica del entorno (que debe considerarse como la distribución de probabilidad de las transiciones de estado), todavía podemos obtener un comportamiento óptimo para maximizar las recompensas.

Como ejemplo, considere el resultado de un lanzamiento de 12 dados. Considerando estos lanzamientos como un solo estado, podemos promediar estos resultados para acercarnos al verdadero resultado predicho. Cuanto más grande sea la muestra, más exactamente nos acercaremos al resultado real esperado.

La cantidad promedio esperada en 12 dados para 60 tiros es 41.57

Este tipo de evaluación basada en muestreo puede parecer familiar para el lector, ya que dicho muestreo también se realiza para sistemas k-bandit. En lugar de comparar diferentes bandidos, los métodos de Monte Carlo se utilizan para comparar diferentes políticas en entornos de Markov, determinando el valor del estado a medida que se sigue una determinada política hasta que se completa el trabajo.

Estimación de Monte Carlo del valor del estado

En el contexto del aprendizaje por refuerzo, los métodos de Monte Carlo son una forma de evaluar la importancia del estado de un modelo promediando los resultados de la muestra. Debido a la necesidad de un estado terminal, los métodos de Monte Carlo son inherentemente aplicables a entornos episódicos. Debido a esta limitación, los métodos de Monte Carlo generalmente se consideran "autónomos" en los que todas las actualizaciones se realizan después de alcanzar el estado terminal. Se puede dar una analogía simple con la búsqueda de una salida de un laberinto: un enfoque autónomo obligaría al agente a llegar al final antes de usar la experiencia intermedia obtenida para intentar reducir el tiempo que lleva atravesar el laberinto. Por otro lado, con el enfoque en línea, el agente cambiará constantemente su comportamiento durante el paso del laberinto, tal vez notará que los corredores verdes conducen a callejones sin salida y decidirá evitarlos, por ejemplo. Discutiremos los enfoques en línea en uno de los siguientes artículos.

El método de Monte Carlo se puede formular de la siguiente manera:

Para comprender mejor cómo funciona el método Monte Carlo, considere el siguiente diagrama de transición de estado. La recompensa por cada transición de estado se muestra en negro, se le aplica un factor de descuento de 0.5. Dejemos de lado el valor real del estado y centrémonos en calcular los resultados de un lanzamiento.

Diagrama de transición de estado. El número de estado se muestra en rojo, el resultado es negro.
Dado que el estado terminal devuelve un resultado igual a 0, calculemos el resultado de cada estado, comenzando con el estado terminal (G5). Tenga en cuenta que hemos establecido el factor de descuento en 0.5, lo que conducirá a una ponderación hacia los estados posteriores.

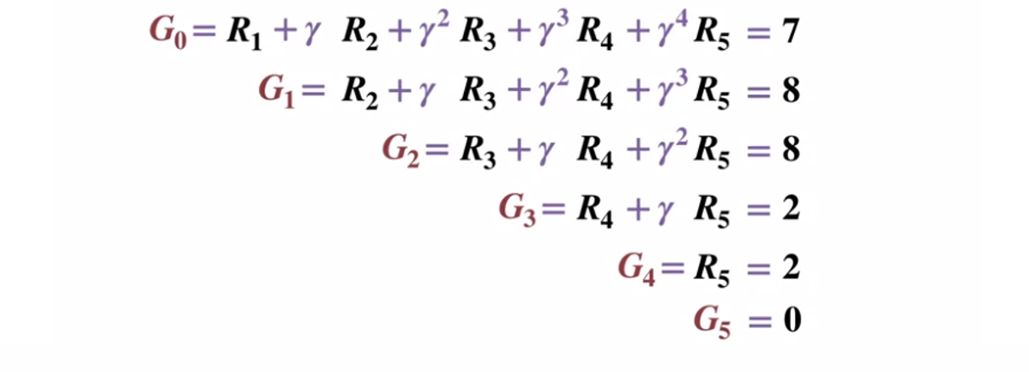
O más generalmente:

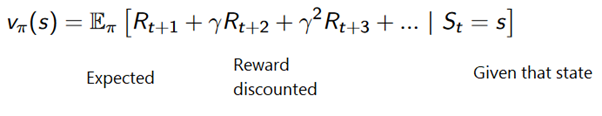
Para evitar almacenar todos los resultados en la lista, podemos realizar el procedimiento de actualización gradual del valor de estado en el método de Monte Carlo, utilizando una ecuación que tenga algunas similitudes con el descenso de gradiente tradicional:

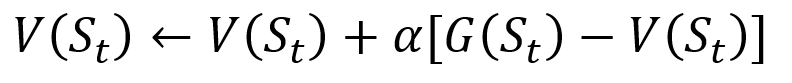Procedimiento de actualización incremental de Monte Carlo. S es el estado, V es su valor, G es su resultado y A es el parámetro del valor del paso.

Como parte del entrenamiento de refuerzo, los métodos de Monte Carlo pueden incluso clasificarse como Primera visita o Cada visita. En resumen, la diferencia entre los dos es cuántas veces se puede visitar un pasaje de un estado antes de la actualización de Monte Carlo. El método de la primera visita de Monte Carlo estima el valor de todos los estados como el valor promedio de los resultados después de visitas individuales a cada estado antes de la finalización, mientras que el método de cada visita de Monte Carlo promedia los resultados después de n visitas hasta la finalización. Utilizaremos la primera visita de Montecarlo a lo largo de este artículo debido a su relativa simplicidad.

Gestión de políticas de Monte Carlo

Si el modelo no puede proporcionar la política, Monte Carlo se puede utilizar para evaluar los valores de acción del estado. Esto es más útil que solo el significado de los estados, ya que la idea del significado de cada acción (q) en un estado dado le permite al agente formular automáticamente una política a partir de observaciones en un entorno desconocido.

Más formalmente, podemos usar Monte Carlo para estimar q (s, a, pi) , el resultado esperado al comenzar desde el estado s, la acción a y la política posterior Pi . Los métodos de Monte Carlo siguen siendo los mismos, excepto que existe una dimensión adicional de las acciones tomadas para un determinado estado. Se cree que se visita un par estado-acción (s, a) durante el paso si alguna vez se visita el estado s y se realiza la acción a en él. Del mismo modo, la evaluación de las acciones de valor puede llevarse a cabo utilizando los enfoques "Primera visita" y "Cada visita".

Al igual que en la programación dinámica, podemos usar una política de iteración generalizada (GPI) para formar una política a partir de la observación de valores de acción estatal.

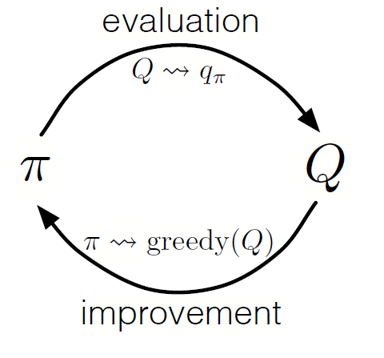
Al alternar los pasos de evaluación de políticas y mejora de políticas, e incluir investigaciones para asegurar que se visiten todas las acciones posibles, podemos lograr la política óptima para cada condición. Para el GPI de Monte Carlo, esta rotación generalmente se realiza después del final de cada pase.

Monte Carlo GPI

Estrategia de blackjack

Para comprender mejor cómo funciona el método de Monte Carlo en la práctica en la tarea de evaluar varios valores de estado, hagamos una demostración paso a paso del juego de blackjack. Para comenzar, determinemos las reglas y condiciones de nuestro juego:

Jugaremos solo contra el crupier, no habrá otros jugadores. Esto nos permitirá considerar las manos del distribuidor como parte del medio ambiente.
El valor de las tarjetas con números iguales a los valores nominales. El valor de las cartas ilustradas: Jack, King y Queen es 10. El valor del as puede ser 1 u 11 dependiendo de la elección del jugador.
Ambas partes reciben dos cartas. Dos cartas de jugador están boca arriba, una de las cartas del crupier también está boca arriba.
El objetivo del juego es que la cantidad de cartas en la mano es <= 21. Un valor mayor que 21 es una quiebra, si ambas partes tienen un valor de 21, entonces el juego se juega en empate.
Después de que el jugador haya visto sus cartas y la primera carta del crupier, el jugador puede elegir tomarle una nueva carta ("todavía") o no ("suficiente") hasta que esté satisfecho con la suma de los valores de la carta en su mano.
Luego, el crupier muestra su segunda carta: si la cantidad resultante es inferior a 17, está obligado a tomar cartas hasta llegar a 17 puntos, después de lo cual ya no toma la carta.

Veamos cómo funciona el método Monte Carlo con estas reglas.

Ronda 1.

Ganas un total de 19. Pero intentas atrapar la suerte por la cola, arriesgarte, obtén 3 y ve a la quiebra. Cuando quebraste, el crupier solo tenía una tarjeta abierta con una suma de 10. Esto se puede representar de la siguiente manera:

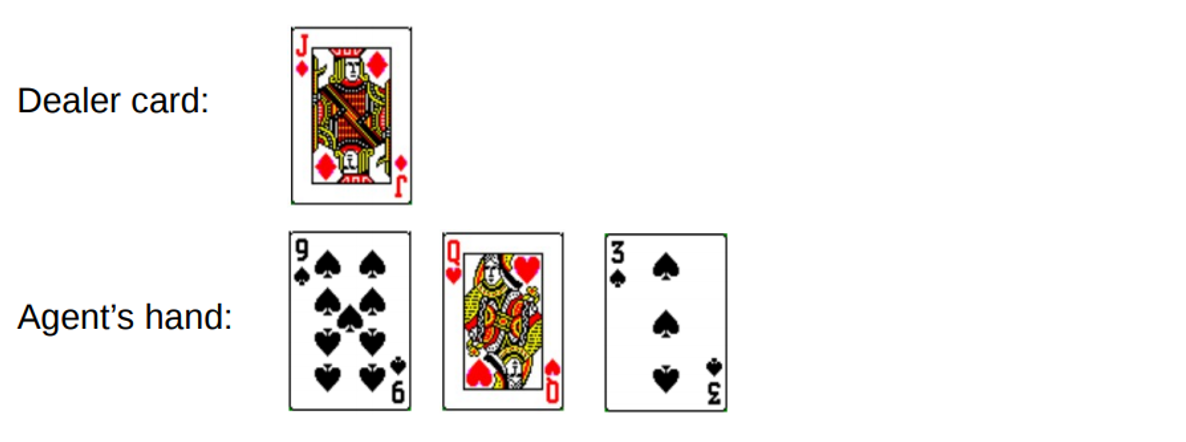
Si vamos a la quiebra, nuestra recompensa por la ronda es -1. Establezcamos este valor como el resultado de retorno del penúltimo estado, usando el siguiente formato [Cantidad de agente, cantidad de distribuidor, as?]:

Bueno, ahora no tenemos suerte. Pasemos a otra ronda.

Ronda 2.

Escribe un total de 19. Esta vez decide detenerse. El crupier marca 13, toma una tarjeta y se arruina. El penúltimo estado se puede describir de la siguiente manera.

Describamos las condiciones y recompensas que recibimos en esta ronda:

Con el final del pasaje, ahora podemos actualizar los valores de todos nuestros estados en esta ronda utilizando los resultados calculados. Tomando un factor de descuento de 1, simplemente distribuimos nuestra nueva recompensa manual, como se hizo con las transiciones de estado anteriores. Como el estado V (19, 10, no) devolvió anteriormente -1, calculamos el valor de retorno esperado y lo asignamos a nuestro estado:

Valores del estado final para la demostración utilizando el blackjack como ejemplo .

Implementación

Escribamos un juego de blackjack usando el método de la primera visita de Monte Carlo para descubrir todos los valores de estado posibles (o varias combinaciones disponibles) en el juego usando Python. Nuestro enfoque se basará en el enfoque de Sudharsan et. al. . Como de costumbre, puede encontrar todo el código del artículo en nuestro GitHub .

Para simplificar la implementación, utilizaremos el gimnasio de OpenAI. Piense en el entorno como una interfaz para iniciar el blackjack con una cantidad mínima de código, esto nos permitirá centrarnos en implementar el aprendizaje reforzado. Convenientemente, toda la información recopilada sobre los estados, acciones y recompensas se almacena en las variables de "observación" , que se acumulan durante las sesiones de juego actuales.

Comencemos importando todas las bibliotecas que necesitamos para obtener y recopilar nuestros resultados.

import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')

Luego, inicialicemos nuestro entorno de gimnasio y definamos una política que coordine las acciones de nuestro agente. De hecho, continuaremos tomando la tarjeta hasta que la cantidad en la mano alcance 19 o más, después de lo cual nos detendremos.

 #Observation here encompassess all data about state that we need, as well as reactions to it env = gym.make('Blackjack-v0') #Define a policy where we hit until we reach 19. # actions here are 0-stand, 1-hit def sample_policy(observation): score, dealer_score, usable_ace = observation return 0 if score >= 19 else 1

Definamos un método para generar datos de pase utilizando nuestra política. Almacenaremos información sobre el estado, las acciones tomadas y la remuneración por la acción.

 def generate_episode(policy, env): # we initialize the list for storing states, actions, and rewards states, actions, rewards = [], [], [] # Initialize the gym environment observation = env.reset() while True: # append the states to the states list states.append(observation) # now, we select an action using our sample_policy function and append the action to actions list action = sample_policy(observation) actions.append(action) # We perform the action in the environment according to our sample_policy, move to the next state observation, reward, done, info = env.step(action) rewards.append(reward) # Break if the state is a terminal state (ie done) if done: break return states, actions, rewards

Finalmente, definamos la función de predicción de Monte Carlo primera visita. Primero, inicializamos un diccionario vacío para almacenar los valores de estado actuales y un diccionario que almacena el número de registros para cada estado en diferentes pases.

 def first_visit_mc_prediction(policy, env, n_episodes): # First, we initialize the empty value table as a dictionary for storing the values of each state value_table = defaultdict(float) N = defaultdict(int)

Para cada pase, llamamos a nuestro método generate_episode para obtener información sobre los valores del estado y las recompensas recibidas después de que ocurra el estado. También inicializamos la variable para almacenar nuestros resultados incrementales. Luego obtenemos la recompensa y el valor del estado actual para cada estado visitado durante el pase, y aumentamos nuestros rendimientos variables por el valor de la recompensa por paso.

 for _ in range(n_episodes): # Next, we generate the epsiode and store the states and rewards states, _, rewards = generate_episode(policy, env) returns = 0 # Then for each step, we store the rewards to a variable R and states to S, and we calculate for t in range(len(states) — 1, -1, -1): R = rewards[t] S = states[t] returns += R # Now to perform first visit MC, we check if the episode is visited for the first time, if yes, #This is the standard Monte Carlo Incremental equation. # NewEstimate = OldEstimate+StepSize(Target-OldEstimate) if S not in states[:t]: N[S] += 1 value_table[S] += (returns — value_table[S]) / N[S] return value_table

Permítame recordarle que, dado que estamos implementando la primera visita de Montecarlo, visitamos un estado en un solo paso. Por lo tanto, hacemos una verificación condicional en el diccionario de estado para ver si el estado ha sido visitado. Si se cumple esta condición, podemos calcular el nuevo valor utilizando el procedimiento definido previamente para actualizar los valores de estado utilizando el método de Monte Carlo y aumentar el número de observaciones para este estado en 1. Luego, repetimos el proceso para el próximo paso para obtener finalmente el valor promedio del resultado .

¡Ejecutemos lo que tenemos y miremos los resultados!

 value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())

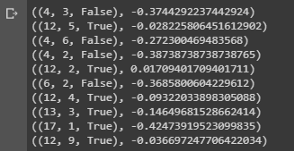Conclusión de una muestra que muestra los valores de estado de varias combinaciones en las manos en el blackjack.

Podemos continuar haciendo observaciones de Monte Carlo para 5000 pases y construir una distribución de valores de estado que describa los valores de cualquier combinación en manos del jugador y el crupier.

 def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])

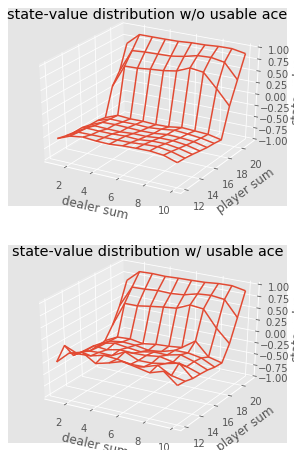Visualización de los valores de estado de varias combinaciones en el blackjack.

Entonces, resumamos lo que aprendimos.

Los métodos de aprendizaje basados en muestreo nos permiten evaluar los valores de estado y acción-estado sin ninguna dinámica de transición, simplemente por muestreo.
Los enfoques de Monte Carlo se basan en un muestreo aleatorio del modelo, observando las recompensas devueltas por el modelo y recolectando información durante la operación normal para determinar el valor promedio de sus estados.
Usando los métodos de Monte Carlo, es posible una política de iteración generalizada.
El valor de todas las combinaciones posibles en manos del jugador y del crupier en el blackjack se puede estimar utilizando múltiples simulaciones de Monte Carlo, allanando el camino para estrategias optimizadas.

Esto concluye la introducción al método de Monte Carlo. En nuestro próximo artículo, pasaremos a los métodos de enseñanza de la forma Aprendizaje de diferencia temporal.

Fuentes:

Sutton y col. al, aprendizaje de refuerzo
White et. al, Fundamentos del aprendizaje por refuerzo, Universidad de Alberta
Silva et. al, aprendizaje por refuerzo, UCL
Platt et. Al, Universidad de Northeaster

Eso es todo. ¡Nos vemos en el curso !

Optimización de estrategia de blackjack de Monte Carlo