Los compiladores de optimización son la base del software moderno: permiten a los programadores escribir código en un lenguaje que entiendan y luego convertirlo en código que el equipo pueda ejecutar de manera eficiente. La tarea de optimizar los compiladores es comprender qué hace el programa de entrada que escribió y crear un programa de salida que haga lo mismo, pero más rápido.
En este artículo, veremos algunas de las técnicas básicas de inferencia en la optimización de compiladores: cómo diseñar un programa con el que el compilador pueda trabajar fácilmente; qué reducciones se pueden hacer en su programa y cómo usarlas para reducirlo y acelerarlo.
Los optimizadores de programa se pueden ejecutar en cualquier lugar: como un paso en un gran proceso de compilación (
Scala Optimizer ); como un programa separado, lanzado después del compilador y antes de la ejecución (
Proguard ); o como parte de un entorno de tiempo de ejecución que optimiza un programa durante su ejecución (
compilador JVM JIT ). Las limitaciones en el trabajo de los optimizadores varían según la situación, pero solo tienen una tarea: tomar el programa de entrada y convertirlo en uno de salida, que hace lo mismo, pero más rápido.
Primero, veremos algunos ejemplos de optimizaciones del borrador del programa, para que comprenda qué suelen hacer los optimizadores y cómo hacerlo todo manualmente. A continuación, un vistazo a algunas formas de programas actuales, y finalmente Examinemos los algoritmos y técnicas que se pueden utilizar para analizar el programa, y luego hacerlos más pequeños y más rápido.
Programa-proyecto
Todos los ejemplos se darán en Java. Este lenguaje es muy común y se compila en un relativamente simple ensamblador -
Java de código de bytes . Por lo tanto, crearemos una buena base, gracias a la cual podemos explorar técnicas de optimización de compilación utilizando ejemplos reales y ejecutables. Todas las técnicas descritas a continuación son aplicables en casi todos los demás lenguajes de programación.
Primero, considere un borrador del programa. Contiene varias lógicas, registra el resultado estándar dentro del proceso y devuelve el resultado calculado. El programa en sí no tiene sentido, pero se utilizará como una ilustración de lo que se puede optimizar mientras se mantiene el comportamiento existente:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Por ahora, suponemos que este programa es todo lo que tenemos, ninguna otra parte del código lo llama. Simplemente ingresa datos en
main , se ejecuta y devuelve el resultado. Ahora optimicemos este programa.
ejemplos de optimizaciones
Tipo de fundición y en línea
Es posible que haya notado que la variable del
logger tiene un tipo inexacto: a pesar de la etiqueta del
logger , según el código, podemos concluir que se trata de una subclase específica:
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
Ahora sabemos que
logger es
PrintLogger , y sabemos que llamar a
logger.log puede tener una única implementación. Puedes en línea:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
Esto reducirá el programa al eliminar la clase innecesaria de
ErrLogger que no se usa, así como al eliminar varios métodos de
log public Logger , ya que lo alineamos en un solo lugar de la llamada.
Constantes de coagulación
Durante la ejecución del programa, el
count y el cambio
total , pero
multiplied no: comienza en
0 y se multiplica cada vez hasta
multiplied = multiplied * count , permaneciendo igual a
0 . Por lo tanto, puede reemplazarlo en todo el programa con
0 :
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Como resultado, vemos que
d1 * multiplied siempre
d1 * multiplied 0 , lo que significa que
total += d1 * multiplied no hace nada y se puede eliminar:
- total += d1 * multiplied
Eliminación de código muerto
Después de doblar
multiplied y darse cuenta de que
total += d1 * multiplied no hace nada, puede eliminar la definición de
int d1 :
- int d1 = ackermann(n, 1);
Esto ya no es parte del programa, y dado que
ackermann es una función pura, la desinstalación no afectará el resultado del programa.
Del mismo modo, después de
logger.log , el
logger ya no se usa y se puede eliminar:
- PrintLogger logger = new PrintLogger();
Remoción de sucursales
Ahora la primera transición condicional en nuestro ciclo depende de
0 < 100 . Como esto siempre es cierto, simplemente puede eliminar la condición:
- if (0 < 100) System.out.println(count); + System.out.println(count);
Cualquier transición condicional que siempre sea verdadera puede estar en línea en el cuerpo de la condición, y para las transiciones que siempre son incorrectas, puede eliminar la condición junto con su cuerpo.
Calculo parcial
Ahora analizamos las tres llamadas restantes a
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- El primero tiene dos argumentos constantes. La función es pura y, tras el cálculo preliminar,
ackermann(2, 2) debe ser igual a 7. - La segunda llamada tiene un argumento constante
0 y uno desconocido n . Puede pasarlo a la definición de ackermann , y resulta que cuando m es 0 , la función siempre devuelve n + 1.
- En la tercera llamada, ambos argumentos son desconocidos:
n count . Vamos a dejarlos en su lugar por ahora.
Dado que la llamada a
ackermann se define de la siguiente manera:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Puedes simplificarlo a:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
Programación tardía
La definición de
d2 usa solo en el
if (count % 2 == 0) condicional
if (count % 2 == 0) . Como el cálculo de
ackermann es limpio, puede transferir esta llamada a una
ackermann condicional para que no se procese hasta que se use:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
Esto evitará la mitad de las llamadas a
ackermann(n, count) , acelerando la ejecución del programa.
A modo de comparación, la función
System.out.println no está limpia, lo que significa que no se puede transferir dentro o fuera de saltos condicionales sin cambiar la semántica del programa.
Resultado optimizado
Una vez recopiladas todas las optimizaciones, obtenemos el siguiente código fuente:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } ); static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Aunque hemos optimizado manualmente, todo esto se puede hacer automáticamente. El siguiente es el resultado descompilado del optimizador de prototipos que escribí para los programas JVM:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
El código descompilado es ligeramente diferente de la versión optimizada manualmente. Algo que el compilador no pudo optimizar (por ejemplo, una llamada no utilizada al
new PrintLogger ), pero algo se hizo de manera un poco diferente (por ejemplo,
ackermann y
ackermann__I__TI1__I ). Pero por lo demás, el optimizador automático hizo lo mismo que yo, utilizando la lógica incorporada en él.
Surge la pregunta: ¿cómo?
Vistas intermedias
Si intenta crear su propio optimizador, la primera pregunta que surja será quizás la más importante: ¿qué es un "programa"?
Sin lugar a dudas, estás acostumbrado a escribir y modificar programas como código fuente. ¿Seguro que les hace en forma de binarios precompilados, tal vez incluso binarios depuradas. Es posible que haya encontrado programas en forma de
árbol de sintaxis ,
código de tres direcciones ,
A-Normal ,
Estilo de paso de continuación o
Asignación estática individual .
Hay todo un zoológico de diferentes representaciones de programas. Aquí discutiremos las formas más importantes de representar un "programa" dentro del optimizador.
Código fuente
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
El código fuente sin compilar también es una representación de su programa. Es relativamente compacto, legible por humanos, pero tiene dos inconvenientes:
- El código fuente contiene todos los detalles de los nombres y el formato, que son importantes para el programador, pero inútiles para la computadora.
- Los programas erróneos en forma de código fuente son mucho más numerosos que los correctos, y durante la optimización debe asegurarse de que su programa se convierta del código fuente de entrada correcto al código fuente de salida correcto.
Estos factores dificultan que el optimizador trabaje con el programa en forma de código fuente. Sí,
puede convertir dicho programa, por ejemplo, utilizando
expresiones regulares para identificar y reemplazar patrones. Sin embargo, el primero de los dos factores dificulta la identificación confiable de patrones con una gran cantidad de detalles extraños. Y el segundo factor aumenta en gran medida la posibilidad de confundirse y obtener un programa resultante incorrecto.
Estas restricciones son aceptables para los convertidores de programas que se ejecutan bajo supervisión humana, por ejemplo, cuando puede usar
Codemod para refactorizar y transformar la base de código. Sin embargo, no puede usar el código fuente como modelo principal de un optimizador automatizado.
Árboles de sintaxis abstracta
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) ) ", BinOp (Ident ( "m"), "-", literal ( static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Los árboles de sintaxis abstracta (AST) es otro formato intermedio común. Se ubican en el siguiente paso de la escalera de abstracción en comparación con el código fuente. Por lo general, AST descarta todo el formato de código fuente, sangría y comentarios, pero conserva los nombres de las variables locales que se descartan en representaciones más abstractas.
Al igual que el código fuente, AST tiene la posibilidad de codificar información innecesaria que no afecta la semántica real del programa. Por ejemplo, los siguientes dos fragmentos de código son semánticamente idénticos; solo difieren en los nombres de las variables locales, pero aún tienen AST diferentes:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
El punto clave es que, aunque los AST tienen una estructura de árbol, contienen nodos que se comportan semánticamente, no como árboles: los valores de
Ident("r") e
Ident("s") determinados por el contenido de sus subárboles, sino por el
Assign("r", ...) ascendente
Assign("r", ...) nodos
Assign("r", ...) y
Assign("s", ...) . De hecho, hay relaciones semánticas adicionales entre
Ident y
Assign que son tan importantes como los bordes en la estructura de árbol AST:

Estas conexiones forman una estructura gráfica generalizada, que incluye ciclos en presencia de definiciones recursivas de funciones.
Bytecode
Como elegimos Java como el idioma principal, los programas compilados se guardan como código de bytes de Java en archivos .class.
Recordemos nuestra función
ackermann :
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Compila a este bytecode:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
La máquina virtual Java (JVM), que ejecuta el bytecode de Java, es una máquina con una combinación de una pila y registros: hay una pila de operandos (STACK) en la que se manipulan los valores y una matriz de variables locales (LOCALS) en la que se pueden almacenar estos valores. La función comienza con N parámetros en las primeras N ranuras de variables locales. A medida que se ejecuta, la función mueve los datos a la pila, los opera, los vuelve a colocar en las variables y llama a
return para devolver el valor a la persona que llama desde la pila de operandos.
Si anota el código de bytes anterior para representar valores que se mueven entre la pila y la tabla de variables locales, se verá así:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Aquí, usando
a0 y
a1 presenté los argumentos de la función, que se almacenan en la tabla LOCALS al comienzo de la función.
1 representa constantes cargadas a través de
iconst_1 , y de
v1 a
v7 , valores intermedios calculados. Hay tres instrucciones de
ireturn que devuelven
v1 ,
v3 y
v7 . Esta función no define otras variables locales, por lo que la matriz LOCALS solo almacena argumentos de entrada.
Arriba, vimos dos variantes de nuestra función:
ackermannA y
ackermannB . Entonces miran en bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | | a0 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
Como el código fuente toma dos argumentos y los pone en variables locales, el código de bytes tiene las instrucciones correspondientes para cargar los valores de los argumentos de los índices LOCALES 0 y 1 y guardarlos en los índices 2 y 3. Sin embargo, el código de bytes no está interesado en los nombres de sus variables locales: funciona con por ellos exclusivamente como con índices en la matriz LOCALS. Por lo tanto,
ackermannA y
ackermannB tendrán
ackermannB idénticos. ¡Esto es lógico, porque son semánticamente equivalentes!
Sin embargo,
ackermannA y
ackermannB no se compilan en el mismo bytecode que el
ackermann original: aunque el bytecode se abstrae de los nombres de las variables locales, aún no se abstrae completamente de cargar y guardar en / desde estas variables. Todavía es importante para nosotros cómo se mueven los valores a lo largo de LOCALS y STACK, aunque no afectan el comportamiento real del programa.
Además de la falta de abstracción de la carga / guardado, el código de bytes tiene otro inconveniente: como la mayoría de los ensambladores lineales, está muy optimizado en términos de compacidad, y puede ser muy difícil modificarlo cuando se trata de optimizaciones.
Para hacerlo más claro, veamos el código de bytes de la función original de
ackermann :
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Hagamos un cambio aproximado: dejemos que la función llame al
30: invokestatic ackermann:(II)I uso su primer argumento. Y luego esta llamada puede ser reemplazada por la llamada equivalente
30: invokestatic ackermann2:(I)I , que toma solo un argumento. Esta es una optimización común, que permite utilizar la "eliminación de código muerto" para descartar cualquier código utilizado para calcular el primer argumento
30: invokestatic ackermann:(II)IPara hacer esto, no solo necesitamos reemplazar la instrucción
30 , sino que también debemos mirar la lista de instrucciones y comprender dónde se calcula el primer argumento (
v4 en
STACK ), y también eliminarlo. Regresamos de las instrucciones
30 a
22 , y de
22 a
21 y
20 . La versión final:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| | | a0 | a1 | BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Todavía podemos hacer un cambio tan simple a una función simple de
ackermann . Pero en las grandes funciones utilizadas en proyectos reales, será mucho más difícil realizar numerosos cambios interconectados. En general, cualquier pequeño cambio semántico en su programa puede requerir numerosos cambios a lo largo del código de bytes.
Puede notar que realizamos el cambio descrito anteriormente al analizar los valores en LOCALS y STACK: vimos cómo
v4 pasa
v4 a la instrucción
30 desde la instrucción
22 , y
22 lleva los datos a
a0 y
1 , que provienen de las instrucciones
21 y
20 . Estos valores se transfieren entre LOCALS y STACK de acuerdo con el principio del gráfico: desde la instrucción que calcula el valor hasta el lugar de su uso posterior.
Al igual que los pares
Ident /
Assign en nuestros AST, los valores que se pasan entre LOCALS y STACK forman un gráfico entre los puntos de cálculo de los valores y los puntos de su uso. Entonces, ¿por qué no comenzamos a trabajar directamente con el gráfico?
Gráficos de flujo de datos
Los gráficos de flujo de datos son el siguiente nivel de abstracción después del bytecode. Si expandimos nuestro árbol de sintaxis con relaciones
Ident /
Assign , o si rastreamos cómo el bytecode mueve los valores entre LOCALS y STACK, podemos construir un gráfico. Para la función de
ackermann se ve así:

A diferencia de AST o Java stack-bytecode bytecode, los gráficos de flujo de datos no utilizan el concepto de "variable local": en cambio, el gráfico contiene enlaces directos entre cada valor y su lugar de uso. Al analizar bytecode, a menudo es necesario interpretar de manera abstracta LOCALS y STACK para comprender cómo se mueven los valores; Análisis del árbol de AST implica el seguimiento y el trabajo con la tabla de caracteres que contiene la conexión
Assign /
Ident ; y el análisis de los gráficos de flujo de datos es a menudo un seguimiento directo de las transiciones, la idea pura de "valores móviles" sin la cáscara de presentar un programa.
ackermann también
ackermann más fáciles de manipular que el código de bytes lineal: reemplazar un nodo con
ackermann con
ackermann2 y
ackermann2 uno de los argumentos es simplemente cambiar el nodo del gráfico (marcado en verde) y eliminar uno de los enlaces de entrada junto con los nodos de tránsito (marcado en rojo):

Como puede ver, un pequeño cambio en el programa (reemplazando
ackermann(int n, int m) por
ackermann2(int m) ) se convierte en un cambio relativamente localizado en el gráfico de flujo de datos.
En general, trabajar con gráficos es mucho más fácil que con bytecode lineal o AST: son fáciles de analizar y cambiar.
No hay muchos detalles en esta descripción de gráficos: además de la representación física real del gráfico, hay muchas otras formas de modelar el control de estado y flujo, que son más difíciles de trabajar y más allá del alcance del artículo. También omití una serie de detalles sobre la transformación de gráficos, por ejemplo, agregar y eliminar enlaces, transiciones hacia adelante y hacia atrás, transiciones horizontales y verticales (en ancho y profundidad), etc. Si estudió algoritmos, entonces todo esto le resultará familiar. .
Finalmente, omitimos los algoritmos de conversión de bytecode lineal a gráfico, y luego de gráfico nuevamente a bytecode. Esto en sí mismo es una tarea interesante, pero se lo dejamos a usted para su estudio independiente.
Análisis
Una vez que tengamos la idea del programa, debemos analizarlo: descubra algunos hechos que le permitirán transformar el programa sin cambiar su comportamiento. Muchas de las optimizaciones discutidas anteriormente se basan en el análisis del programa:
- Plegado constante: ¿El resultado de la expresión funciona con un valor constante conocido? ¿Es puro el cálculo de la expresión?
- Tipo de conversión y en línea: ¿una llamada a método es un tipo con una sola implementación del método llamado?
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
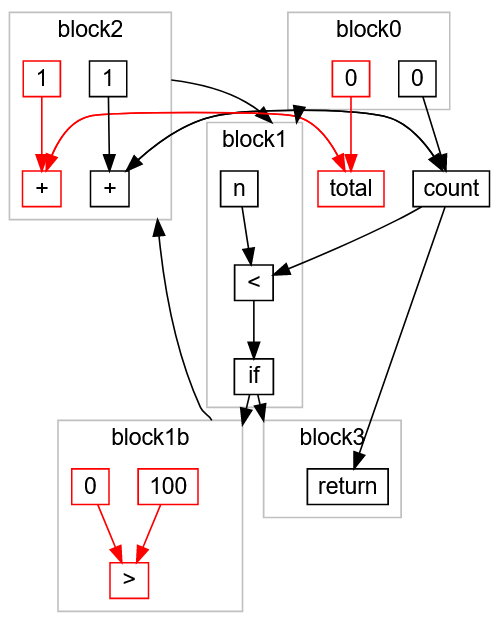
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . :

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
Conclusión
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :