Continúo publicando mis conferencias, originalmente destinadas a estudiantes que estudian en la especialidad de "geología digital". Esta es la tercera publicación del ciclo en el centro, el primer artículo fue introductorio, no es necesario que se lea. Sin embargo, para comprender este artículo, es necesario leer la introducción a los sistemas lineales de ecuaciones, incluso si sabe lo que es, ya que me referiré mucho a ejemplos de esta introducción.

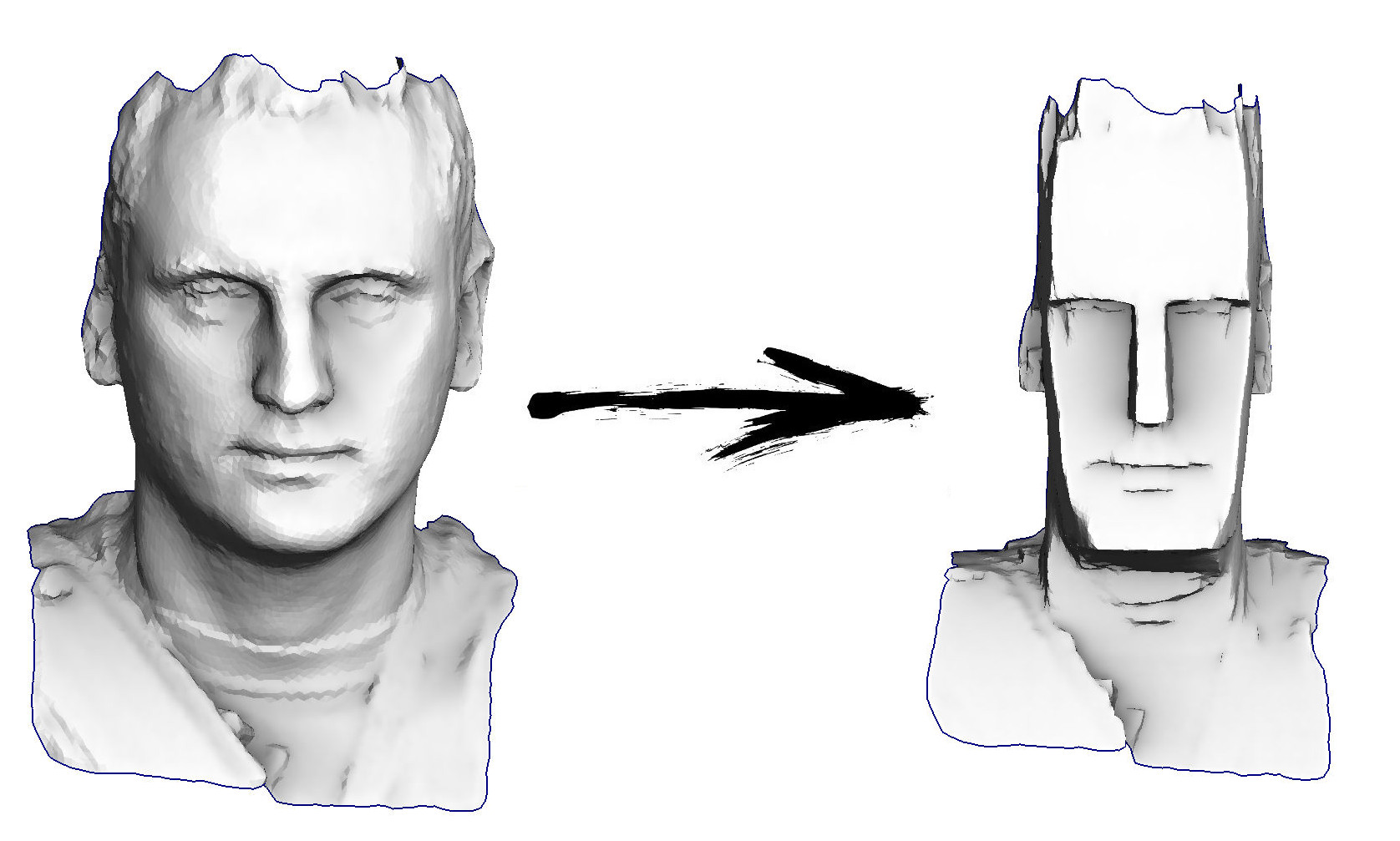
Entonces, la tarea de hoy: aprender el procesamiento de geometría más simple, por ejemplo, para poder transformar mi cabeza en un ídolo de la Isla de Pascua:



Plan de conferencias actual:

• Programa educativo sobre teoría de la probabilidad (artículo introductorio, opcional)
  
• Introducción a los sistemas lineales de ecuaciones.
  
• Minimización de formas cuadráticas y ejemplos de problemas de MCO
  
• De mínimos cuadrados a redes neuronales
  

El repositorio oficial del curso vive aquí . El libro aún no está terminado, estoy compilando lentamente artículos publicados en Habré.

En este artículo, mi herramienta principal será encontrar el mínimo de funciones cuadráticas; pero antes de comenzar a usar esta herramienta, debe al menos comprender dónde tiene el botón de encendido / apagado. Primero, actualice la memoria y recuerde qué son las matrices, qué es un número positivo y también qué es una derivada.

Matrices y numeros

En este texto utilizaré abundantemente la notación matricial, así que recordemos de qué se trata. No busque más en el texto, haga una pausa por unos segundos e intente formular qué es una matriz.

Diferentes interpretaciones matriciales

La respuesta es muy simple. La matriz es solo un gabinete en el que se almacena el rábano picante. Cada mierda se encuentra en su celda, las celdas se agrupan en filas en filas y columnas. En nuestro caso particular, los números reales habituales son basura; la forma más fácil para un programador $$$A$ como algo

float A[m][n]; 

¿Por qué se necesitan tales almacenamientos? ¿Qué describen ellos? Tal vez te moleste, pero la matriz en sí misma no describe nada, almacena. Por ejemplo, en él puedes almacenar los coeficientes de cualquier función. Olvidémonos de las matrices por un segundo e imaginemos que tenemos un número $$$a$ . Que significa Sí, el demonio lo sabe ... Por ejemplo, puede ser un coeficiente dentro de una función que toma un número como entrada y da otro número como salida:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

Un matemático podría escribir una versión de una función como

$$

$$f (x) = hacha$$

Bueno, en el mundo de los programadores, se vería así:

 float f(float x) { return a*x; } 

Por otro lado, ¿por qué tal función, y no otra muy distinta? ¡Tomemos otro!

$$

$$f (x) = ax ^ 2$$

Desde que comencé con los programadores, debo escribir su código :)

 float f(float x) { return x*a*x; } 

Una de estas funciones es lineal, y la segunda es cuadrática. ¿Cuál es el correcto? No, el número mismo $$$a$ no lo define, ¡solo almacena algo de valor! ¿Qué función necesitas? Crea una como esa.

Lo mismo sucede con las matrices, estos son almacenamientos necesarios en caso de que no haya suficientes números individuales (escalares), una especie de expansión de números. Por encima de las matrices, al igual que sobre los números, se definen las operaciones de suma y multiplicación.

Imaginemos que tenemos una matriz $$$A$ Por ejemplo, tamaño 2x2:

$$

$$A = \ begin {bmatrix} a_ {11} y a_ {12} \\ a_ {21} y a_ {22} \ end {bmatrix}$$

Esta matriz en sí misma no significa nada, por ejemplo, puede interpretarse como una función.

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

Esta función convierte un vector bidimensional en un vector bidimensional. Gráficamente, es conveniente presentar esto como conversión de imagen: le damos la imagen a la entrada, y en la salida obtenemos su versión estirada y / o girada (¡posiblemente incluso reflejada!). Muy pronto daré una imagen con varios ejemplos de tal interpretación de matrices.

Y puede la matriz $$$A$ imagine como una función que convierte un vector bidimensional en un escalar:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

Tenga en cuenta que la exponenciación no está muy definida con vectores, por lo que no puedo escribir $$$x ^ 2$ , como escribió en el caso de los números ordinarios. Recomiendo encarecidamente a aquellos que no están acostumbrados a hacer malabarismos fácilmente con las multiplicaciones de matrices, una vez más, recordar la regla de multiplicación de matrices y verificar que la expresión $$$x ^ \ arriba A x$ generalmente permitido y realmente da un escalar a la salida. Para hacer esto, por ejemplo, puede poner corchetes explícitamente $$$x ^ \ top A x = (x ^ \ top A) x$ . Te recuerdo que tenemos $$$x$ Es un vector de dimensión 2 (almacenado en una matriz de dimensión 2x1), escribimos explícitamente todas las dimensiones:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

Volviendo al mundo cálido y esponjoso de los programadores, podemos escribir la misma función cuadrática algo como esto:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

¿Qué es un número positivo?

Ahora haré una pregunta muy estúpida: ¿qué es un número positivo? Ya tenemos una gran herramienta llamada predicado $$$>$ . Pero tómate tu tiempo para contestar ese número $$$a$ positivo si y solo si $$$a> 0$ Eso sería muy fácil. Definamos la positividad de la siguiente manera:

Definición 1

Numero $$$a$ positivo si y solo si para todo real distinto de cero $$$x \ in \ mathbb R, \ x \ neq 0$ la condición está satisfecha $$$ax ^ 2> 0$ .

Parece bastante complicado, pero se aplica perfectamente a las matrices:

Definición 2

Matriz cuadrada $$$A$ se llama positivo definido si, para cualquier no cero $$$x$ la condición está satisfecha $$$x ^ \ top A x> 0$ es decir, la forma cuadrática correspondiente es estrictamente positiva en todas partes, excepto en el origen.

¿Por qué necesito positividad? Como mencioné al principio del artículo, mi herramienta principal será buscar los mínimos de las funciones cuadráticas. Pero al menos para buscar, ¡no sería malo si existiera! Por ejemplo, una función $$$f (x) = - x ^ 2$ obviamente, el mínimo no existe, ya que el número -1 no es positivo, y $$$f (x)$ disminuye sin cesar con el crecimiento $$$x$ : ramas de una parábola $$$f (x)$ mira hacia abajo Las matrices definidas positivas son buenas porque las formas cuadráticas correspondientes forman un paraboloide que tiene un mínimo (único). La siguiente ilustración muestra siete ejemplos diferentes de matrices. $$$2 \ por 2$ , tanto positivo como simétrico, y no es así. Fila superior: interpretación de matrices como funciones $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . Fila central: interpretación de matrices como funciones $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



Por lo tanto, trabajaré con matrices definidas positivas, que son una generalización de números positivos. Además, específicamente en mi caso, ¡las matrices también serán simétricas! Es curioso que, con frecuencia, cuando las personas hablan de certeza positiva, también se refieren a la simetría, que puede explicarse indirectamente por la siguiente observación (opcional para comprender el texto posterior).

Digresión lírica sobre la simetría de matrices de formas cuadráticas.

Veamos la forma cuadrática. $$$x ^ \ top M x$ para una matriz arbitraria $$$M$ ; luego a $$$M$ suma e inmediatamente resta la mitad de su versión transpuesta:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

Matriz $$$M_s$ simétrico: $$$M_s ^ \ top = M_s$ ; matriz $$$M_a$ antisimétrico: $$$M_a ^ \ top = -M_a$ . Un hecho notable es que para cualquier matriz antisimétrica, la forma cuadrática correspondiente es idénticamente igual a cero. Esto se desprende de la siguiente observación:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

Es decir, la forma cuadrática $$$x ^ \ top M_a x$ simultáneamente igual $$$q$ y $$$-q$ , que solo es posible cuando $$$q \ equiv 0$ . De este hecho se deduce que para una matriz arbitraria $$$M$ forma cuadrática correspondiente $$$x ^ \ top M x$ puede expresarse a través de una matriz simétrica $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x. $$$

Estamos buscando un mínimo de una función cuadrática

Regresemos brevemente al mundo unidimensional; Quiero encontrar un mínimo de funciones $$$f (x) = ax ^ 2 - 2bx$ . Numero $$$a$ positivamente, por lo tanto, existe un mínimo; para encontrarlo, equiparamos a cero la derivada correspondiente: $$$\ frac {d} {dx} f (x) = 0$ . Diferenciar la función cuadrática unidimensional del trabajo no es: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; entonces nuestro problema se reduce a resolver la ecuación $$$ax-b = 0$ , donde, a través de terribles esfuerzos, obtenemos una solución $$$x ^ * = b / a$ . La siguiente figura ilustra la equivalencia de dos problemas: solución $$$x ^ *$ ecuaciones $$$ax-b = 0$ coincide con la solución de la ecuación $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



Tiendo al hecho de que nuestro objetivo global es minimizar las funciones cuadráticas, pero estamos hablando de mínimos cuadrados. Pero al mismo tiempo, lo que realmente sabemos hacer bien es resolver ecuaciones lineales (y sistemas de ecuaciones lineales). ¡Y es genial que uno sea equivalente al otro!

Lo único que nos queda es asegurarnos de que esta equivalencia en el mundo unidimensional se extienda al caso $$$n$ variables Para verificar esto, primero probamos tres teoremas.

Tres teoremas, o expresiones matriciales diferenciadas

El primer teorema establece que las matrices $$$1 \ por 1$ invariantes con respecto a la transposición:

Teorema 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

La prueba es tan complicada que tengo que omitirla por brevedad, pero trate de encontrarla usted mismo.

El segundo teorema nos permite diferenciar funciones lineales. En el caso de una función real de una variable, sabemos que $$$\ frac {d} {dx} (bx) = b$ pero que pasa en el caso de una función real $$$n$ variables?

Teorema 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

Es decir, sin sorpresas, solo una grabación matricial del mismo resultado escolar. La prueba es extremadamente sencilla, solo escriba la definición del gradiente:

$$

$$\ nabla (b ^ \ top x) = \ begin {bmatrix} \ frac {\ partial (b ^ \ top x)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (b ^ \ top x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ frac {\ partial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_1} \\ \ vdots \\ \ frac {\ parcial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

Aplicando el primer teorema $$$b ^ \ top x = x ^ \ top b$ , completamos la prueba.

Ahora pasamos a formas cuadráticas. Sabemos que en el caso de una función real de una variable $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ , y ¿qué pasará en el caso de una forma cuadrática?

Teorema 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

Por cierto, tenga en cuenta que si la matriz $$$A$ simétrico, entonces el teorema dice que $$$\ nabla (x ^ \ top A x) = 2Ax$ .

Esta prueba también es sencilla, solo escribe la forma cuadrática como una suma doble:

$$

$$x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

Y luego veamos cuál es la derivada parcial de esta doble suma con respecto a la variable $$$x_i$ :
\ begin {align *}
\ frac {\ partial (x ^ \ top A x)} {\ partial x_i}
& = \ frac {\ partial} {\ partial x_i} \ left (\ sum \ limits_ {k_1} \ sum \ limits_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ right) = \\
& = \ frac {\ partial} {\ partial x_i} \ left (
\ underbrace {\ sum \ limits_ {k_1 \ neq i} \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + \ underbrace {\ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ right) = \\
& = \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ sum \ limits_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ sum \ limits_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
Dividí la suma doble en cuatro casos, que se destacan con llaves. Cada uno de estos cuatro casos se diferencia trivialmente. Queda por hacer la última acción, recoger las derivadas parciales en el vector gradiente:

$$

$$\ nabla (x ^ \ top A x) = \ begin {bmatrix} \ frac {\ partial (x ^ \ top Ax)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (x ^ \ top A x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ sum \ limits_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limits_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

El mínimo de la función cuadrática y la solución del sistema lineal.

No olvidemos la dirección del viaje. Vimos eso con un número positivo $$$a$ en el caso de funciones reales de una variable, resuelva la ecuación $$$ax = b$ o minimizar la función cuadrática $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ Son una y la misma cosa.

Queremos mostrar la conexión correspondiente en el caso de una matriz simétrica positiva definida $$$A$ .
Entonces queremos encontrar el mínimo de la función cuadrática

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

Exactamente como en la escuela, equiparamos la derivada a cero:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

El operador de Hamilton es lineal, por lo que podemos reescribir nuestra ecuación de la siguiente forma:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Ahora aplicamos los teoremas de diferenciación segunda y tercera:

$$

$$(A + A ^ \ top) x - 2b = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Recordemos que $$$A$ simétrica, y dividiendo la ecuación en dos, obtenemos el sistema de ecuaciones lineales que necesitamos:

$$

$$Ax = b$$

¡Hurra, pasando de una variable a muchas, no hemos perdido nada en absoluto, y podemos minimizar efectivamente las funciones cuadráticas!

Pasamos a los mínimos cuadrados

Finalmente, podemos pasar al contenido principal de esta conferencia. Imagina que tenemos dos puntos en un avión $$$(x_1, y_1)$ y $$$(x_2, y_2)$ , y queremos encontrar la ecuación de una línea que pasa por estos dos puntos. La ecuación de la línea se puede escribir como $$$y = \ alpha x + \ beta$ , es decir, nuestra tarea es encontrar los coeficientes $$$\ alpha$ y $$$\ beta$ . Este ejercicio es para el séptimo y octavo grado de la escuela, escribimos el sistema de ecuaciones:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ right. $$$

Tenemos dos ecuaciones con dos incógnitas ( $$$\ alpha$ y $$$\ beta$ ), el resto es conocido.

En el caso general, existe una solución y es única. Por conveniencia, reescribimos el mismo sistema en forma matricial:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

Obtenemos una ecuación de tipo $$$Ax = b$ que se resuelve trivialmente $$$x ^ * = A ^ {- 1} b$ .

Ahora imagine que tenemos tres puntos a través de los cuales necesitamos dibujar una línea recta:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {split} \ right . $$$

En forma matricial, este sistema se escribe de la siguiente manera:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \, (3 \ times 2)} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \, (2 \ times 1)} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \, (3 \ por 1)}$$

Ahora tenemos una matriz $$$A$ rectangular, y simplemente no existe al revés! Esto es completamente normal, ya que solo tenemos dos variables y tres ecuaciones, y en el caso general este sistema no tiene solución. Esta es una situación completamente normal en el mundo real, cuando los puntos son datos de mediciones ruidosas, y necesitamos encontrar los parámetros $$$\ alpha$ y $$$\ beta$ los mejores datos de medición aproximados Ya consideramos este ejemplo en la primera clase, cuando se calibró la romana. Pero entonces nuestra solución fue puramente algebraica y muy engorrosa. Probemos de una manera más intuitiva.

Nuestro sistema se puede escribir de la siguiente manera:

$$

$$\ alpha \ underbrace {\ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ begin {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

O, más brevemente,

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}. $$$

Vectores $$$\ vec i$ , $$$\ vec j$ y $$$\ vec b$ conocido, necesita encontrar escalares $$$\ alpha$ y $$$\ beta$ .
Obviamente combinación lineal $$$\ alpha \ vec {i} + \ beta \ vec {j}$ genera un plano, y si el vector $$$\ vec b$ no se encuentra en este plano, entonces no hay una solución exacta; Sin embargo, estamos buscando una solución aproximada.

Definamos el error de decisión como $$$\ vec {e} (\ alpha, \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . Nuestro objetivo es encontrar dichos valores de parámetros $$$\ alpha$ y $$$\ beta$ que minimizan la longitud del vector $$$\ vec {e} (\ alpha, \ beta)$ . En otras palabras, el problema se escribe como $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ .
Aquí hay una ilustración:.



Habiendo dado vectores $$$\ vec i$ , $$$\ vec j$ y $$$\ vec b$ , tratamos de minimizar la longitud del vector de error $$$\ vec e$ . Obviamente, su longitud se minimiza si es perpendicular al plano estirado sobre los vectores. $$$\ vec i$ y $$$\ vec j$ .

Pero espera, ¿dónde están los mínimos cuadrados? Ahora lo serán. Función de extracción de raíz $$$\ sqrt {\ cdot}$ monótono por lo tanto $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ !

Es bastante obvio que la longitud del vector de error se minimiza si es perpendicular al plano estirado sobre los vectores. $$$\ vec i$ y $$$\ vec j$ , que se puede escribir igualando a cero los productos escalares correspondientes:

$$

$$\ left \ {\ begin {split} \ vec {i} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alfa, \ beta) & = 0 \ end {split} \ right. $$$

En forma matricial, este mismo sistema se puede escribir como

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ alpha \ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + \ beta \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

o si no

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

Pero no nos detendremos allí, ya que el registro puede reducirse aún más:

$$

$$A ^ \ top (Ax - b) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix}$$

Y la transformación más reciente:

$$

$$A ^ \ top Ax = A ^ \ top b. $$$

Calculemos las dimensiones. Matriz $$$A$ tiene tamaño $$$3 \ por 2$ por lo tanto $$$A ^ \ top A$ tiene tamaño $$$2 \ por 2$ . Matriz $$$b$ tiene tamaño $$$3 \ por 1$ pero vector $$$A ^ \ top b$ tiene tamaño $$$2 \ por 1$ . Es decir, en el caso general, la matriz $$$A ^ \ top A$ reversible! Por otra parte, $$$A ^ \ top A$ Tiene un par de buenas propiedades.

Teorema 4

$$$A ^ \ top A$ simétrico

Esto no es del todo difícil de mostrar:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

Teorema 5

$$$A ^ \ top A$ positivamente semi-definido: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

Esto se desprende del hecho de que $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

También $$$A ^ \ top A$ positivo definido si $$$A$ tiene columnas linealmente independientes (rango $$$A$ igual al número de variables en el sistema).

En total, para un sistema con dos incógnitas, demostramos que la minimización de una función cuadrática $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ equivalente a resolver un sistema de ecuaciones lineales $$$A ^ \ top A x = A ^ \ top b$ . Por supuesto, todo este razonamiento se aplica a cualquier otro número de variables, pero volvamos a escribir todo junto de forma compacta con un simple cálculo algebraico. Comenzamos con el problema de los mínimos cuadrados, llegamos a la minimización de la función cuadrática de la forma familiar, y de esto concluimos que es equivalente a resolver un sistema de ecuaciones lineales. Entonces, vamos:

$$

$$\ begin {split} \ mathrm {argmin} \ | Ax - b \ | ^ 2 & = \ mathrm {argmin} (Ax-b) ^ \ top (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ top) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Ax - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Ax) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ phantom {} ^ \ top x) \ end {split}$$

Entonces, el problema de los mínimos cuadrados $$$\ mathrm {argmin} \ | Hacha - b \ | ^ 2$ equivalente a minimizar una función cuadrática $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ con (en el caso general) una matriz definida positiva simétrica $$$A '$ , que, a su vez, es equivalente a resolver un sistema de ecuaciones lineales $$$A'x = b '$ . Uff La teoría ha terminado.

Pasemos a practicar

Ejemplo uno, unidimensional

Recordemos un ejemplo de un artículo anterior :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

Tenemos una matriz x normal de 32 elementos, inicializados de la siguiente manera:



Y luego realizaremos el siguiente procedimiento mil veces: para cada celda x [i] escribimos el valor promedio de las celdas vecinas: x [i] = (x [i-1] + x [i + 1]) / 2. La única excepción: no reescribiremos los elementos de la matriz con los números 0, 18 y 31. Así es como se ve la evolución de la matriz en las primeras ciento cincuenta iteraciones:



Como descubrimos en el artículo anterior , resulta que nuestro megacódigo de código de Python de cuatro líneas resuelve el siguiente sistema de ecuaciones lineales por el método de Gauss-Seidel:



Lo descubrieron, pero ¿de dónde vino este sistema? Que tipo de magia Divaguemos por un segundo e intentemos resolver un sistema ligeramente diferente. Todavía tengo 32 variables, pero ahora quiero que todas sean iguales entre sí. Esto no es difícil de escribir, es suficiente escribir un sistema de ecuaciones que establezca que todos los elementos vecinos son iguales en pares:



El código de Python anterior, en principio, no toca los valores de tres variables: x0, x18, x31, así que transfiéralos al lado derecho del sistema de ecuaciones, es decir, excluir del conjunto de incógnitas:



Arreglo el valor inicial x0 = 1, la primera ecuación dice x1 = x0 = 1, la segunda ecuación dice x2 = x1 = x0 = 1 y así sucesivamente, hasta llegar a la ecuación 1 = x0 = x17 = x18 = 2 Oh Pero este sistema no tiene solución: ((

Y no importa, ¡somos programadores! ¡Llamemos a los mínimos cuadrados para obtener ayuda! Nuestro sistema insoluble puede escribirse en forma de matriz. $$$Ax = b$ ; para resolver nuestro sistema aproximadamente, es suficiente resolver el sistema $$$A^\top Ax=A^\top b$ .¡Y luego resulta que este es exactamente el sistema de ecuaciones uno a uno del artículo anterior!

Intuitivamente, uno puede imaginar el proceso de crear una matriz de un sistema de la siguiente manera: conectamos por resortes los valores cuyas igualdades queremos alcanzar. Por ejemplo, en nuestro caso, queremos$$x yo era igual$x_i$$$x i + 1 , entonces agregamos la ecuación$x_{i+1}$$$x i - x i + 1 = 0 , colgando entre estos valores un resorte que los juntará. Pero dado que los valores de x0, x18 y x31 están firmemente fijados, no queda nada para los valores libres más que estirar los resortes de manera uniforme, produciendo (en este caso) una solución lineal por partes. Escribamos un programa que resuelva este sistema de ecuaciones. En el último artículo, vimos que el método Gauss-Seidel es muy simple en la programación, pero tiene una convergencia muy lenta, por lo que sería mejor usar solucionadores reales de sistemas de ecuaciones lineales. En el caso más simple, para nuestro ejemplo unidimensional, el código puede verse así:$x_i - x_{i+1}=0$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

Este código produce una lista x de 32 elementos en los que se almacena la solución. Estamos construyendo una matriz$$A , construyendo un vector$A$$$b , obtenemos un vector con una solución$b$$$x = ( A ⊤ A ) - 1 A ⊤ b , y luego insertamos nuestros valores fijos x0 = 1, x18 = 2 y x31 = 1 en este vector. Este código hace el trabajo necesario, pero es bastante desagradable transferir los valores de las variables fijas al lado derecho. ¿Es posible hacer trampa? Usted puede! Veamos el siguiente código:$x = (A^\top A)^{-1}A^\top b$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

Desde el punto de vista del programador, es mucho más agradable, el vector x se obtiene inmediatamente de la dimensión requerida, y las matrices A y b se completan mucho más fácilmente. Pero cual es el truco? Escribamos el sistema de ecuaciones que resolvemos:



mira cuidadosamente las últimas tres ecuaciones:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

¿Podría ser más fácil escribirlas de la siguiente manera?
x0 = 1
x18 = 2
x31 = 1

No, no es más fácil. Como ya dije, cada ecuación cuelga resortes, en este caso, el resorte entre x0 y el valor 1, el resorte entre x18 y el valor 2, y finalmente, la variable x31 también se sentirá atraída por la unidad.

Pero el coeficiente de 100 está ahí por una razón. Recordamos que este sistema simplemente no se puede resolver, lo resolvemos en el sentido de mínimos cuadrados, minimizando la función cuadrática correspondiente. Multiplicando por 100 cada uno de los coeficientes de las últimas tres ecuaciones, introducimos una penalización por desviarse x0, x18 y x32 de los valores deseados, diez mil veces (100 ^ 2) excediendo la penalización por desviarse de la igualdad$$$x_i = x_{i+1}$ .Hablando en términos generales, los resortes en las últimas tres ecuaciones son diez mil veces más difíciles que en todas las demás. Este método de penalización cuadrática es una herramienta muy conveniente para introducir restricciones; es mucho más simple (aunque no sin inconvenientes) que reducir un conjunto de variables.

Ejemplo dos, tridimensional

¡Pasemos a algo más interesante que suavizar los elementos de una matriz unidimensional! Para empezar, haremos exactamente lo mismo, pero con datos más interesantes y con herramientas reales. Quiero tomar una superficie tridimensional, arreglar su borde y suavizar el resto de la superficie tanto como sea posible:



el código está disponible aquí , pero en caso de que proporcione una lista completa del archivo principal:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Escribí el analizador más simple de archivos .obj wavefront, por lo que el modelo se carga en una línea. Como solucionador, usaré OpenNL, es un solucionador muy poderoso para problemas de mínimos cuadrados con matrices dispersas. Tenga en cuenta que las dimensiones de las matrices pueden ser gigantescas: por ejemplo, si queremos obtener una imagen en blanco y negro con un tamaño de 1000 x 1000 píxeles, entonces la matriz$$A ⊤ A tendremos el tamaño de un millón por millón! Sin embargo, en la práctica, con frecuencia la gran mayoría de los elementos de esta matriz son cero, por lo que no todo es tan aterrador, pero aún debe utilizar solucionadores especiales. Así que echemos un vistazo al código. Para comenzar, le anuncio al solucionador lo que quiero hacer:$A^\top A$

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

Quiero tener una matriz $$A ⊤ A en tamaño (número de vértices) x (número de vértices). Atención, le damos al solucionador una matriz$A^\top A$$$A y$A$$$A ⊤ A lo construirá él mismo, ¡lo cual es muy conveniente! Además, preste atención al hecho de que no resuelvo un sistema de ecuaciones, sino tres en serie para x, y y z (¡mentí que el problema es tridimensional, sigue siendo unidimensional!)Y luego declaro fila por fila de nuestra matriz. Para comenzar, arreglo los vértices que están en el borde de la superficie:$A^\top A$

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

Puedes ver que estoy usando una penalización cuadrada de 100 ^ 2 para arreglar los vértices del borde.

Bueno, entonces para cada par de vértices adyacentes cuelgo un resorte de rigidez 1 entre ellos:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

Ejecutamos el código y vemos cómo la cara se alisó en la superficie de la película de jabón en un alambre curvo. Acabamos de resolver el problema de Dirichlet, habiendo obtenido una superficie de área mínima.

Mejoramos las caracteristicas

Convirtamos nuestra cara en una máscara grotesca:



en el artículo anterior ya mostré cómo hacer esto en la rodilla, aquí doy un código real que usa el solucionador de mínimos cuadrados:

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

El código completo está disponible aquí . Como trabaja el Como en el ejemplo anterior, empiezo arreglando los vértices del borde. Luego, para cada borde I (en silencio, con un coeficiente de 0.2) digo que sería bueno si tuviera exactamente la misma forma que en la superficie original:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

Si no hace nada más y resuelve el problema tal como es, entonces deberíamos obtener exactamente lo que estaba en la salida en la salida: el borde de salida es igual al borde de entrada, además las diferencias en la salida son iguales a las diferencias en la entrada.

¡Pero no nos detendremos allí!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

Agrego más ecuaciones a nuestro sistema. Para cada vértice, cuento la curvatura de la superficie a su alrededor en la superficie de entrada y la multiplico por dos y medio, es decir, la superficie de salida debe tener una gran curvatura en todas partes.

Luego llamamos a nuestro solucionador y obtenemos una buena caricatura.

Último ejemplo para hoy

Hasta este momento, no hemos visto un solo nuevo ejemplo, todo ya se mostró en el artículo anterior. Intentemos hacer algo menos trivial que el suavizado más simple, que puede obtenerse fácilmente sin usar ningún solucionador. El código está disponible aquí , pero déjame darte una lista:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Todavía estamos trabajando en la misma superficie que antes; llamamos a la función snap () para cada triángulo. Esta función dice qué eje del sistema de coordenadas está más cerca de la normalidad de este triángulo. Es decir, queremos saber que este triángulo es más probable que sea vertical u horizontal. Bueno, ¡entonces queremos cambiar la geometría de nuestra superficie para que lo que está cerca de la horizontal se acerque aún más! La parte izquierda de esta imagen muestra el resultado de la función snap ():



Entonces, pintamos nuestra superficie en tres colores, correspondientes a los tres ejes del sistema de coordenadas. Bueno, entonces para cada borde de nuestro sistema agregamos las siguientes ecuaciones:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

Es decir, le ordenamos a cada borde de la superficie de salida que se parezca al borde correspondiente de la superficie de entrada, la rigidez del resorte 1. Y luego, si permitimos, por ejemplo, la dimensión x, y el borde debe ser vertical, entonces simplemente decimos que un vértice es igual al otro con la rigidez del resorte 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

Bueno, aquí está el resultado de nuestro programa: una



pregunta perfectamente razonable: ídolos de Isla de Pascua, esto, por supuesto, es genial, pero ¿qué tiene que ver la geología con él? ¿Hay ejemplos de problemas reales?

Si por supuesto. Tomemos una sección de la corteza terrestre:



para los geólogos, las capas de diferentes rocas son muy importantes, los límites (horizontes) entre los cuales se muestran en verde y las fallas geológicas que se muestran en rojo. Tenemos en la entrada una cuadrícula de triángulos (tetraedros en 3D) del área que nos interesa, pero se necesitan quads (hexaedros en 3D) para modelar ciertos procesos. Deformamos nuestro modelo para que las fallas se vuelvan verticales y los horizontes (sorpresa) horizontales:



Luego, simplemente tomamos una cuadrícula regular de cuadrados, cortamos nuestro dominio en cuadrados uniformes y les aplicamos la transformación inversa, obteniendo la cuadrícula de quads necesaria.

Conclusión

Los métodos de mínimos cuadrados son una poderosa herramienta de procesamiento de datos, y se usan mucho más ampliamente que las estadísticas en las columnas de Excel. Estas posibilidades se nos abren debido al hecho de que minimizar una función cuadrática y resolver un sistema de ecuaciones lineales es lo mismo, y nosotros (la humanidad) hemos aprendido a resolver ecuaciones lineales muy, muy bien, incluso tamaños completamente inhumanos con miles de millones de variables.

Sin embargo, hay momentos en que es posible que no tengamos suficientes modelos lineales. Y aquí, por ejemplo, las redes neuronales pueden venir al rescate. En el próximo artículo, intentaré demostrar que los OLS con rechazo de emisiones son equivalentes a una de las formulaciones de redes neuronales. ¡Quédate en la línea!