RayTracing comprensible en 256 líneas de C ++ desnudo
Este es otro capítulo de mi breve curso de conferencias sobre gráficos por computadora . Esta vez estamos hablando del trazado de rayos. Como de costumbre, trato de evitar las bibliotecas de terceros, ya que creo que hace que los estudiantes verifiquen lo que sucede debajo del capó. Consulte también el proyecto tinykaboom .
Hay muchos artículos de trazado de rayos en la web; sin embargo, el problema es que casi todos muestran software terminado que puede ser bastante difícil de entender. Tomemos, por ejemplo, el muy famoso desafío de trazado de rayos de la tarjeta de negocios . Produce programas muy impresionantes, pero es muy difícil entender cómo funciona esto. En lugar de mostrar que puedo hacer renders, quiero contarte en detalle cómo puedes hacerlo tú mismo.
Nota: no tiene sentido mirar mi código ni leer este artículo con una taza de té en la mano. Este artículo está diseñado para que usted tome el teclado e implemente su propio motor de renderizado. Seguramente será mejor que el mío. ¡Al menos cambie el lenguaje de programación!
Por lo tanto, el objetivo de hoy es aprender a representar esas imágenes:

Paso 1: escribe una imagen en el disco
No quiero molestarme con los administradores de ventanas, el procesamiento del mouse / teclado y cosas así. El resultado de nuestro programa será una simple imagen guardada en el disco. Entonces, lo primero que debemos poder hacer es guardar la imagen en el disco. Aquí puede encontrar el código que nos permite hacer esto. Déjame enumerar el archivo principal:
#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; }
Solo se llama a render () en la función principal y nada más. ¿Qué hay dentro de la función render ()? En primer lugar, defino el framebuffer como una matriz unidimensional de valores Vec3f, esos son simples vectores tridimensionales que nos dan valores (r, g, b) para cada píxel. La clase de vectores vive en el archivo geometry.h, no lo describiré aquí: es realmente una manipulación trivial de vectores bidimensionales y tridimensionales (suma, resta, asignación, multiplicación por un producto escalar, escalar).
Guardo la imagen en formato ppm . Es la forma más fácil de guardar imágenes, aunque no siempre es la forma más conveniente de verlas más. Si desea guardar en otros formatos, le recomiendo que vincule una biblioteca de terceros, como stb . Esta es una gran biblioteca: solo necesita incluir un archivo de encabezado stb_image_write.h en el proyecto, y le permitirá guardar imágenes en los formatos más populares.
Advertencia: mi código está lleno de errores, los soluciono en el flujo ascendente, pero las confirmaciones anteriores se ven afectadas. Revisa este problema .
Entonces, el objetivo de este paso es asegurarnos de que podemos a) crear una imagen en la memoria + asignar diferentes colores yb) guardar el resultado en el disco. Luego puede verlo en un software de terceros. Aquí está el resultado:

Paso 2, el crucial: trazado de rayos
Este es el paso más importante y difícil de toda la cadena. Quiero definir una esfera en mi código y dibujarla sin estar obsesionada con los materiales o la iluminación. Así es como debería verse nuestro resultado:

Por conveniencia, tengo un commit por paso en mi repositorio; Github hace que sea muy fácil ver los cambios realizados. Aquí, por ejemplo , lo que cambió la segunda confirmación.
Para empezar, ¿qué necesitamos para representar la esfera en la memoria de la computadora? Cuatro números son suficientes: un vector tridimensional para el centro de la esfera y un escalar que describe el radio:
struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } };
Lo único no trivial en este código es una función que le permite verificar si un rayo dado (que se origina en orig en la dirección de dir) se cruza con nuestra esfera. Puede encontrar una descripción detallada del algoritmo para la intersección de la esfera de rayos aquí , le recomiendo que haga esto y verifique mi código.
¿Cómo funciona el trazado de rayos? Es bastante simple En el primer paso, simplemente llenamos la imagen con un degradado de colores:
for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } }
Ahora para cada píxel formaremos un rayo que viene del origen y pasa a través de nuestro píxel, y luego verificaremos si este rayo se cruza con la esfera:

Si no hay intersección con la esfera, dibujamos el píxel con color1, de lo contrario con color2:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8);
En este punto, le recomiendo que tome un lápiz y verifique en papel todos los cálculos (la intersección de la esfera de rayos y el barrido de la imagen con los rayos). Por si acaso, nuestra cámara está determinada por lo siguiente:
- ancho de la imagen
- altura de la imagen
- ángulo del campo de visión
- ubicación de la cámara, Vec3f (0.0.0)
- ver la dirección, a lo largo del eje z, en la dirección de menos infinito
Permítanme ilustrar cómo calculamos la dirección inicial del rayo para trazar. En el bucle principal tenemos esta fórmula:
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
De donde viene? Bastante simple Nuestra cámara se coloca en el origen y se enfrenta a la dirección -z. Permítanme ilustrar las cosas, esta imagen muestra la cámara desde arriba, el eje y apunta fuera de la pantalla:
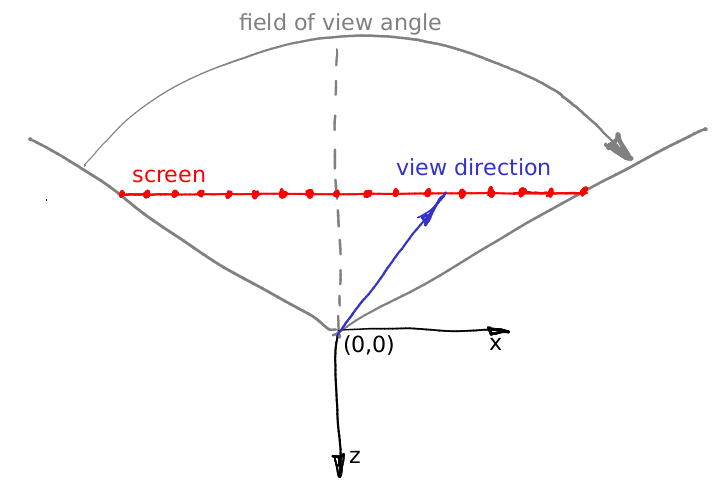
Como dije, la cámara se coloca en el origen y la escena se proyecta en la pantalla que se encuentra en el plano z = -1. El campo de visión especifica qué sector del espacio será visible en la pantalla. En nuestra imagen, la pantalla tiene 16 píxeles de ancho; ¿Puedes calcular su longitud en coordenadas mundiales? Es bastante simple: centrémonos en el triángulo formado por la línea discontinua roja, gris y gris. Es fácil ver que el bronceado (campo de visión / 2) = (ancho de pantalla) 0.5 / (distancia de pantalla-cámara). Colocamos la pantalla a la distancia de 1 de la cámara, por lo tanto (ancho de pantalla) = 2 tan (campo de visión / 2).
Ahora digamos que queremos proyectar un vector a través del centro del duodécimo píxel de la pantalla, es decir, queremos calcular el vector azul. ¿Cómo podemos hacer eso? ¿Cuál es la distancia desde la izquierda de la pantalla hasta la punta del vector azul? En primer lugar, tiene 12 + 0.5 píxeles. Sabemos que 16 píxeles de la pantalla corresponden a 2 unidades mundiales tan (fov / 2). Por lo tanto, la punta del vector está ubicada en (12 + 0.5) / 16 2 unidades mundiales (tan (fov / 2)) desde el borde izquierdo, o en la distancia de (12 + 0.5) 2/16 * tan (fov / 2) - tan (fov / 2) desde la intersección entre la pantalla y el eje -z. Agregue la relación de aspecto de la pantalla a los cálculos y encontrará exactamente las fórmulas para la dirección del rayo.
Paso 3: agrega más esferas
La parte más difícil ha terminado, y ahora nuestro camino está despejado. Si sabemos cómo dibujar una esfera, no nos llevará mucho tiempo agregar algunas más. Verifique los cambios en el código, y esta es la imagen resultante:

Paso 4: iluminación
La imagen es perfecta en todos los aspectos, excepto por la falta de luz. En el resto del artículo hablaremos sobre iluminación. Agreguemos algunas fuentes de luz puntuales:
struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; };
Calcular la iluminación global real es una tarea muy, muy difícil, por lo que, como todos los demás, engañaremos al ojo dibujando resultados completamente no físicos, pero visualmente plausibles. Para empezar: ¿por qué hace frío en invierno y calor en verano? Porque el calentamiento de la superficie de la Tierra depende del ángulo de incidencia de los rayos solares. Cuanto más alto sale el sol sobre el horizonte, más brillante es la superficie. Por el contrario, cuanto más bajo está por encima del horizonte, más tenue es. Y después de que el sol se pone en el horizonte, los fotones ni siquiera nos alcanzan.
Retroceda nuestras esferas: emitimos un rayo desde la cámara (¡sin relación con los fotones!) Cuando se detiene en una esfera. ¿Cómo sabemos la intensidad de la iluminación del punto de intersección? De hecho, es suficiente verificar el ángulo entre un vector normal en este punto y el vector que describe una dirección de la luz. Cuanto más pequeño es el ángulo, mejor se ilumina la superficie. Recuerde que el producto escalar entre dos vectores ayb es igual al producto de normas de vectores multiplicado por el coseno del ángulo entre los vectores: a * b = | a | | b | cos (alfa (a, b)). Si tomamos vectores de longitud unitaria, el producto de puntos nos dará la intensidad de la iluminación de la superficie.
Por lo tanto, en la función cast_ray, en lugar de un color constante, devolveremos el color teniendo en cuenta las fuentes de luz:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; }
Las modificaciones del paso anterior están disponibles aquí , y aquí está el resultado:

Paso 5: iluminación especular
El truco del producto de puntos ofrece una buena aproximación de la iluminación de superficies mate, en la literatura se llama iluminación difusa. ¿Qué debemos hacer si queremos dibujar superficies brillantes? Quiero obtener una foto como esta:

Comprueba las pocas modificaciones necesarias. En resumen, cuanto más brillante sea la luz en las superficies brillantes, menor será el ángulo entre la dirección de la vista y la dirección de la luz reflejada .
Este truco con iluminación de superficies mates y brillantes se conoce como modelo de reflexión de Phong . La wiki tiene una descripción bastante detallada de este modelo de iluminación. Puede ser agradable leerlo junto con el código fuente. Aquí está la imagen clave para entender la magia:

Paso 6: sombras
¿Por qué tenemos la luz, pero no las sombras? No esta bien! Quiero esta foto:

Solo seis líneas de código nos permiten lograr esto: al dibujar cada punto, solo nos aseguramos de que el segmento entre el punto actual y la fuente de luz no se cruza con los objetos de nuestra escena. Si hay una intersección, omitimos la fuente de luz actual. Solo hay una pequeña sutileza: perturbo el punto moviéndolo en la dirección normal:
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
¿Por qué es eso? Es solo que nuestro punto se encuentra en la superficie del objeto y (a excepción de la cuestión de los errores numéricos) cualquier rayo de este punto se cruzará con el objeto mismo.
Paso 7: reflexiones
Es increíble, pero para agregar reflexiones a nuestro render, solo necesitamos agregar tres líneas de código:
Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Véalo usted mismo: al intersecar la esfera, simplemente calculamos el rayo reflejado (¡con la ayuda de la misma función que usamos para los reflejos especulares!) Y llamamos recursivamente a la función cast_ray en la dirección del rayo reflejado. Asegúrate de jugar con la profundidad de recursión , la configuré en 4, prueba diferentes valores que comienzan con 0, ¿qué cambiará en la imagen? Aquí está mi resultado con reflexiones y una profundidad de recursión de 4:

Paso 8: refracciones
Si sabemos hacer reflexiones, las refracciones son fáciles . Necesitamos agregar una función para calcular el rayo refractado ( usando la ley de Snell ), y tres líneas más de código en nuestra función recursiva cast_ray. Aquí está el resultado donde la bola más cercana está "hecha de vidrio", refleja y refracta la luz al mismo tiempo:

Steo 9: más allá de las esferas
Hasta este momento, representamos solo esferas porque es uno de los objetos matemáticos no triviales más simples. Agreguemos un plano. El tablero de ajedrez es una opción clásica. Para este propósito, es suficiente agregar una docena de líneas .
Y aquí está el resultado:

Según lo prometido, el código tiene 256 líneas de código, ¡ compruébelo usted mismo !
Paso 10: asignación de casa
Hemos recorrido un largo camino: hemos aprendido cómo agregar objetos a una escena, cómo calcular una iluminación bastante complicada. Déjame dejarte dos tareas como tarea. Absolutamente todo el trabajo preparatorio ya se ha hecho en la sucursal tarea_asignación . Cada tarea requerirá diez líneas de código superior.
Tarea 1: mapa del entorno
Por el momento, si el rayo no se cruza con ningún objeto, simplemente configuramos el píxel con el color de fondo constante. ¿Y por qué, en realidad, es constante? ¡Tomemos una foto esférica (archivo envmap.jpg ) y úsela como fondo! Para facilitar la vida, vinculé nuestro proyecto con la biblioteca stb para la conveniencia de trabajar con el formato jpg. Debería darnos esa imagen:

Tarea 2: quack-quack!
Podemos representar tanto esferas como planos (ver el tablero de ajedrez). ¡Entonces dibujemos mallas triangulares! Escribí un código que le permite leer un archivo .obj y le agregué una función de intersección de triángulo de rayos. Ahora agregar el pato a nuestra escena debería ser bastante trivial:

Conclusión
Mi objetivo principal es mostrar proyectos que sean interesantes (¡y fáciles!) De programar. Estoy convencido de que para convertirse en un buen programador hay que hacer muchos proyectos paralelos. No sé sobre ti, pero personalmente no me atraen el software de contabilidad y el juego de buscaminas, incluso si la complejidad del código es bastante comparable.
Pocas horas y doscientas cincuenta líneas de código nos dan un trazador de rayos. Se pueden hacer quinientas líneas del rasterizador de software en unos pocos días. ¡Los gráficos son realmente geniales para aprender la programación!