Clon Numpy

Un pequeño módulo para trabajar con matrices en Python sin usar bibliotecas de terceros (un clon NumPy, pero solo en Python puro).

Se le pidió a la tarea en la universidad que escribiera un programa que calcule las normas y las descomposiciones de la matriz, pero se le prohibió usar bibliotecas de terceros. La elección del lenguaje de programación no está limitada. Elegí python (que fue un error, porque es mucho más lento que Java y C / C ++) y, en consecuencia, no puedo usar NumPy. En el proceso, tuve que escribir funciones para realizar operaciones con matrices, funciones para encontrar menores, determinantes, etc. El resultado es una mini biblioteca para trabajar con matrices.

Mi código de Python puro es mucho más lento que NumPy, que hace cálculos de C y Fortran (además mi código no está optimizado).

¿Qué puede MatLOL:

• Suma, diferencia y producto de matrices.
• Producto matricial por número
• Transposición de matriz
• Matriz menor
• Matriz determinante
• Matriz inversa
• Matriz de la unión
• Número de condición de la matriz
• La primera, segunda (no finalizada), normas de matriz euclidiana e infinita
• Solución de la ecuación AX = B
• Descomposición LU
• Descomposición de Cholesky
• Método Seidel

Ejemplos MathLOL

Importar el módulo:

# from mathlol import * from mathlol import mathlol 

Inicialización de la matriz

 matrix = mathlol() matrix.set([[1, 2, 3], [4, 5, 6], [7, -8, 9]]) matrix.get() #   

Algunas operaciones matriciales

 matrix * 2 #     2 A = [[0, 0, 0], [0, 1, 0], [0, 0, 0]] #  2  matrix.dot(A) matrix * A matrix.transposition() #   matrix.minor(i = 0, j = 0) #   matrix.determinant() #   matrix.inverse() #   L, U = matrix.lu() # LU  matrix.seidel(b = [[5.0], [9.0], [1.0]]) #   

También hay funciones para trabajar con vectores.

 vector = mathlol() vector.set([1, 2, 3, 4, 5]) vector.checkvector() # ,     vector.norm1_vector() vector.norm2_vector() vector.norm3_vector() 

Otros ejemplos

Rendimiento MathLOL

Veamos la velocidad de calcular productos de matrices de tamaño NxN. Las matrices están llenas de enteros aleatorios de -100 a 100.




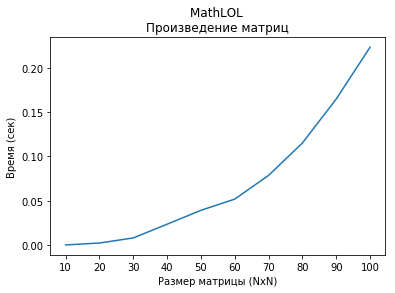
La velocidad de cálculo de tamaños de productos de matriz de 100x100 a 1000x1000



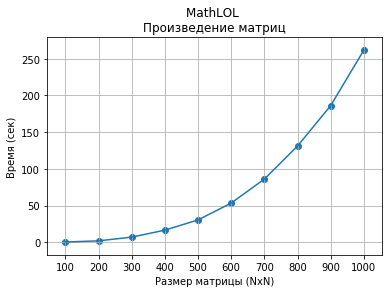
Compare la velocidad computacional de numpy y mathlol. Desafortunadamente, el mathlol era muy lento en velocidad y decidí tomar matrices para tamaños de matriz numpy de 100x100 a 1000x1000, y para mathlol de 10x10 a 100x100.



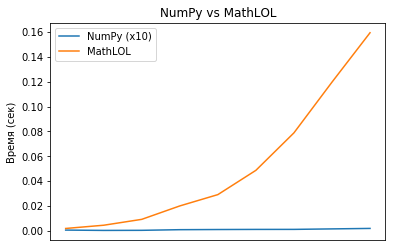
MathLOL calculó el producto de la matriz 100x100 por sí mismo en 0.16 segundos, y NumPy calculó el producto de la matriz 1000x1000 por sí mismo en 0.002 (!!!) segundos. La diferencia es enorme

Nuestra tarea era simplemente implementar varias funciones para trabajar con matrices, lo cual hicimos, pero el programa con matrices grandes no funciona tan rápido como nos gustaría. Queda por refinar el programa, agregar algunas funciones más (por ejemplo, una función para calcular el número de Todd), le agradecería si mira el código, señala errores y tal vez ayuda a refinar el código.

Eso es todo, el código y los ejemplos se publican en el github .

PD: En el proceso de escribir el artículo, quería experimentar e incrustar C / C ++ en mi módulo. Me ocuparé de esto en un futuro próximo y veré qué tan cerca estará del rendimiento de NumPy.