
En octubre, se celebró el segundo campeonato de programación. Recibimos 12,500 solicitudes, más de 6,000 personas probaron suerte en las competiciones. Esta vez, los participantes pudieron elegir una de las siguientes pistas: backend, frontend, desarrollo móvil y aprendizaje automático. En cada pista, se requería pasar la etapa de calificación y la final.
Por tradición, publicaremos análisis de pistas en Habré. Comencemos con las tareas de la fase de calificación del aprendizaje automático. El equipo preparó cinco de esas tareas, de las cuales había dos opciones para tres tareas: en la primera versión había tareas A1, B1 y C, en la segunda - A2, B2 y C. Las opciones se distribuyeron al azar entre los participantes. El autor de la tarea C es nuestro desarrollador Pavel Parkhomenko, el resto de las tareas fueron realizadas por su colega Nikita Senderovich.
Para la primera tarea algorítmica simple (A1 / A2), los participantes podrían obtener 50 puntos enumerando correctamente la respuesta. Para la segunda tarea (B1 / B2) dimos de 10 a 100 puntos, dependiendo de la efectividad de la solución. Para obtener 100 puntos, fue necesario implementar el método de programación dinámica. La tercera tarea se dedicó a construir un modelo de clic basado en los datos de capacitación proporcionados. Se requiere aplicar métodos de trabajo con atributos categóricos y usar un modelo no lineal de entrenamiento (por ejemplo, aumento de gradiente). Para la tarea, fue posible obtener hasta 150 puntos, dependiendo del valor de la función de pérdida en la muestra de prueba.
A1. Restaurar la longitud del carrusel
Condición
El sistema de recomendación debería determinar efectivamente los intereses de las personas. Y además de los métodos de aprendizaje automático, se utilizan soluciones de interfaz especiales para realizar esta tarea, que preguntan explícitamente al usuario qué es lo que le interesa. Una de esas soluciones es el carrusel.
Un carrusel es una cinta horizontal de tarjetas, cada una de las cuales ofrece suscribirse a una fuente o tema específico. La misma carta se puede encontrar en el carrusel varias veces. El carrusel se puede desplazar de izquierda a derecha, mientras que después de la última tarjeta, el usuario vuelve a ver la primera. Para el usuario, la transición de la última tarjeta a la primera es invisible, desde su punto de vista, la cinta es interminable.
En algún momento, un usuario curioso, Vasily, notó que la cinta estaba colocada y decidió averiguar la longitud real del carrusel. Para hacer esto, comenzó a desplazarse a través de la cinta y escribir secuencialmente las tarjetas de reunión, por simplicidad, designando cada tarjeta con una letra latina en minúscula. Entonces Vasily escribió las primeras n tarjetas en un pedazo de papel. Se garantiza que miró todas las tarjetas de carrusel al menos una vez. Entonces Vasily se fue a la cama, y por la mañana descubrió que alguien había derramado un vaso de agua sobre sus notas y ahora algunas letras no podían ser reconocidas.
Según la información restante, ayude a Vasily a determinar el menor número posible de tarjetas en el carrusel.
Formatos de E / S y ejemplosFormato de entrada
La primera línea contiene un número entero n (1 ≤ n ≤ 1000): el número de caracteres escritos por Vasily.
La segunda línea contiene la secuencia escrita por Vasily. Se compone de n caracteres: letras latinas en minúsculas y el signo #, lo que significa que la letra en esta posición no se puede reconocer.
Formato de salida
Imprima un solo número positivo entero: el número más pequeño posible de tarjetas en el carrusel.
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 4
Notas
En el primer ejemplo, se reconocieron todas las letras, el carrusel mínimo podría consistir en 3 cartas: abc.
En el segundo ejemplo, se reconocieron todas las letras, el carrusel mínimo podría consistir en 3 cartas: abb. Tenga en cuenta que la segunda y la tercera carta en este carrusel son iguales.
En el tercer ejemplo, la longitud de carrusel más pequeña posible se obtiene si suponemos que el símbolo a estaba en la tercera posición. Entonces la línea inicial es ababa, el carrusel mínimo consta de 2 cartas - ab.
En el cuarto ejemplo, la cadena de origen podría ser cualquier cosa, por ejemplo ffffff. Entonces el carrusel podría consistir en una tarjeta: f.
Sistema de calificación
Solo después de pasar todas las pruebas para la tarea puede obtener
50 puntos .
En el sistema de prueba, las pruebas 1–4 son ejemplos de la condición.
Solución
Fue suficiente para clasificar la longitud posible del carrusel de 1 a n y para cada longitud fija comprobar si podía ser así. Está claro que la respuesta siempre existe, ya que el valor de n está garantizado como una posible respuesta. Para una longitud fija de carrusel p, es suficiente verificar que en la cadena transmitida para todo i de 0 a (p - 1) en todas las posiciones i, i + p, i + 2p, etc., se encuentren los mismos caracteres o #. Si al menos para algunos i hay 2 caracteres diferentes del rango de la a a la z, entonces el carrusel no puede tener la longitud p. Como en el peor de los casos, para cada p, debe ejecutar todos los caracteres de la cadena una vez, la complejidad de este algoritmo es O (n
2 ).
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2. Restaurar la longitud del carrusel
Condición
El sistema de recomendación debería determinar efectivamente los intereses de las personas. Y además de los métodos de aprendizaje automático, se utilizan soluciones de interfaz especiales para realizar esta tarea, que preguntan explícitamente al usuario qué es lo que le interesa. Una de esas soluciones es el carrusel.
Un carrusel es una cinta horizontal de tarjetas, cada una de las cuales ofrece suscribirse a una fuente o tema específico. La misma carta se puede encontrar en el carrusel varias veces. El carrusel se puede desplazar de izquierda a derecha, mientras que después de la última tarjeta, el usuario vuelve a ver la primera. Para el usuario, la transición de la última tarjeta a la primera es invisible, desde su punto de vista, la cinta es interminable.
En algún momento, un usuario curioso, Vasily, notó que la cinta estaba colocada y decidió averiguar la longitud real del carrusel. Para hacer esto, comenzó a desplazarse a través de la cinta y escribir secuencialmente las tarjetas de reunión, por simplicidad, designando cada tarjeta con una letra latina en minúscula. Entonces Vasily escribió las primeras n cartas. Se garantiza que miró todas las tarjetas de carrusel al menos una vez. Como Vasily estaba distraído por el contenido de las tarjetas, al escribir, podía reemplazar por error una letra con otra, pero se sabe que en total no cometió más que k errores.
Las grabaciones hechas por Vasily cayeron en tus manos; también conoces el valor de k. Determine qué pocas tarjetas podría haber en su carrusel.
Formatos de E / S y ejemplosFormato de entrada
La primera línea contiene dos enteros: n (1 ≤ n ≤ 500) - el número de caracteres escritos por Basil, yk (0 ≤ k ≤ n) - el número máximo de errores que cometió Vasily.
La segunda línea contiene n letras minúsculas del alfabeto latino, la secuencia escrita por Vasily.
Formato de salida
Imprima un solo número positivo entero: el número más pequeño posible de tarjetas en el carrusel.
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 4
Notas
En el primer ejemplo, k = 0, y sabemos con certeza que Vasily no se equivocó, el carrusel mínimo podría consistir en 3 cartas: abc.
En el segundo ejemplo, la longitud de carrusel más pequeña posible se obtiene si suponemos que Vasily reemplazó por error la tercera letra a con c. Entonces la línea real es ababa, el carrusel mínimo consta de 2 cartas - ab.
En el tercer ejemplo, se sabe que Vasily podría cometer un error. Sin embargo, el tamaño del carrusel es mínimo, suponiendo que no cometió errores. El carrusel mínimo consta de 3 cartas: abb. Tenga en cuenta que la segunda y la tercera carta en este carrusel son iguales.
En el cuarto ejemplo, podemos decir que Vasily se equivocó al ingresar todas las letras, y la línea original podría ser cualquiera, por ejemplo ffffff. Entonces el carrusel podría consistir en una tarjeta: f.
Sistema de calificación
Solo después de pasar todas las pruebas para la tarea puede obtener
50 puntos .
En el sistema de prueba, las pruebas 1–4 son ejemplos de la condición.
Solución
Fue suficiente para clasificar la longitud posible del carrusel de 1 a n y para cada longitud fija comprobar si podía ser así. Está claro que la respuesta siempre existe, ya que el valor de n está garantizado como una respuesta posible, sea cual sea el valor de k. Para una longitud de carrusel fija p, es suficiente calcular, independientemente para todo i de 0 a (p - 1), cuál es el número mínimo de errores cometidos en las posiciones i, i + p, i + 2p, etc. Este número de errores es mínimo si se toma como verdadero el símbolo es el que se encuentra en estas posiciones con mayor frecuencia. Entonces el número de errores es igual al número de posiciones en las que se encuentra otra letra. Si para algunos p el número total de errores no excede k, entonces el valor p es una posible respuesta. Dado que para cada p necesita revisar todos los caracteres de la cadena una vez, la complejidad de este algoritmo es O (n
2 ).
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1 Cinta de recomendación óptima
Condición
La formación de la siguiente parte de la emisión personal de recomendaciones para el usuario no es una tarea fácil. Considere n publicaciones seleccionadas de una base de recomendaciones basada en la selección de candidatos. El número de publicación i se caracteriza por una puntuación de relevancia s
i y un conjunto de k atributos binarios a
i1 , a
i2 , ..., a
ik . Cada uno de estos atributos corresponde a alguna propiedad de la publicación, por ejemplo, si el usuario está suscrito a la fuente de esta publicación, si la publicación se creó en las últimas 24 horas, etc. La publicación puede tener varias de estas propiedades a la vez, en cuyo caso los atributos correspondientes toman el valor 1, o puede que no tenga ninguno de ellos, y luego todos sus atributos son 0.
Para que el feed del usuario sea diverso, es necesario elegir entre m candidatos n publicaciones para que entre ellas haya al menos publicaciones A
1 que tengan la primera propiedad, al menos publicaciones A
2 que tengan la segunda propiedad, ..., publicaciones A
k que tengan la propiedad de número k. Encuentre el puntaje de relevancia total máximo posible para m publicaciones que cumplan con este requisito, o determine que tal conjunto de publicaciones no existe.
Formatos de E / S y ejemplosFormato de entrada
La primera línea contiene tres enteros: n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
Las siguientes n líneas muestran las características de las publicaciones. La publicación i-ésima recibe un número entero s
i (1 ≤ s
i ≤ 10
9 ): una evaluación de la relevancia de esta publicación, y luego un espacio de k caracteres, cada uno de los cuales es 0 o 1, es el valor de cada uno de los atributos de esta publicación.
La última línea contiene k enteros separados por espacios: los valores A
1 , ..., A
k (0 ≤ A
i ≤ m) que definen los requisitos para el conjunto final de m publicaciones.
Formato de salida
Si no hay un conjunto de m publicaciones que satisfagan las restricciones, imprima el número 0. De lo contrario, imprima un solo número entero positivo: el puntaje máximo de relevancia total posible.
Ejemplo 1
Ejemplo 2
Notas
En el primer ejemplo, de cuatro publicaciones con dos propiedades, se deben seleccionar dos para que haya al menos una publicación que tenga la primera propiedad y otra que tenga la segunda propiedad. La mayor cantidad de relevancia se puede obtener si tomamos la segunda y la tercera publicación, aunque cualquier opción con una cuarta publicación también es adecuada para restricciones.
En el segundo ejemplo, es imposible seleccionar dos publicaciones para que ambas tengan la segunda propiedad, porque solo la primera publicación la tiene.
Sistema de calificación
Las pruebas para esta tarea consisten en cinco grupos. Los puntos para cada grupo se otorgan solo al pasar todas las pruebas del grupo y todas las pruebas de grupos
anteriores . Pasar las pruebas de las condiciones es necesario para obtener puntos para los grupos a partir de la segunda. En total para la tarea puede obtener
100 puntos .
En el sistema de prueba, las pruebas 1-2 son ejemplos de la condición.
1.
(10 puntos) pruebas 3–10: k = 1, m ≤ 3, s
i ≤ 1000, no se requieren pruebas de la condición
2.
(20 puntos) pruebas 11–20: k ≤ 2, m ≤ 3
3.
(20 puntos) pruebas 21–29: k ≤ 2
4.
(20 puntos) pruebas 30–37: k ≤ 3
5.
(30 puntos) pruebas 38–47: sin restricciones adicionales
Solución
Hay n publicaciones, cada una tiene velocidad y k banderas booleanas, es necesario seleccionar m tarjetas de modo que la suma de relevancias sea máxima yk los requisitos de la forma "entre las m publicaciones seleccionadas deben tener ≥ A
i tarjetas con la i-ésima bandera" o cumplirlas tal conjunto de publicaciones no existe.
La decisión es de 10 puntos : si hay exactamente una bandera, es suficiente tomar publicaciones A
1 con esta bandera que sean de la mayor relevancia (si hay menos cartas de este tipo que A
1 , entonces el conjunto deseado no existe), y el resto (m - A
1 ) son tomadas por las restantes. tarjetas con la mejor relevancia.
La solución es de 30 puntos : si m no excede de 3, entonces puede encontrar la respuesta mediante una búsqueda exhaustiva de todos los triples de O (n
3 ) posibles, elija la mejor opción en términos de relevancia total que satisfaga las restricciones.
La decisión es de 70 puntos (50 puntos es lo mismo, solo que más fácil de implementar): si no hay más de 3 indicadores, puede dividir todas las publicaciones en 8 grupos disjuntos de acuerdo con el conjunto de indicadores que tienen: 000, 001, 010, 011, 100, 101, 110, 111. Las publicaciones en cada grupo deben clasificarse en orden descendente de relevancia. Luego, para O (m
4 ), podemos clasificar cuántas mejores publicaciones tomamos de los grupos 111, 011, 110 y 101. De cada una tomamos de 0 a m publicaciones, en total no más de m. Después de eso, queda claro cuántas publicaciones deben recopilarse de los grupos 100, 010 y 001 para satisfacer los requisitos. Queda por llegar a m con las cartas restantes con la mayor relevancia.
Solución completa : considere la función de programación dinámica dp [i] [a] ... [z]. Este es el puntaje máximo de relevancia total que se puede obtener usando exactamente i publicaciones para que exista exactamente una publicación con bandera A, ..., z publicaciones con bandera Z. Luego, inicialmente dp [0] [0] ... [0] = 0, y para todos los demás conjuntos de parámetros, establecemos el valor igual a -1 para maximizar este valor en el futuro. A continuación, "entraremos en el juego" tarjetas una a la vez y usaremos cada tarjeta para mejorar los valores de esta función: para cada estado de dinámica (i, a, b, ..., z) usando la publicación j-ésima con banderas (a
j , b
j , ..., z
j ), podemos intentar hacer una transición al estado (i + 1, a + a
j , b + b
j , ..., z + z
j ) y verificar si el resultado mejora en este estado. Importante: durante la transición, no estamos interesados en estados donde i ≥ m, por lo tanto, los estados totales de dicha dinámica no son más que m
k + 1 , y el comportamiento asintótico resultante es O (nm
k + 1 ). Cuando se calculan los estados de dinámica, la respuesta es un estado que satisface las restricciones y proporciona el puntaje de relevancia total más alto.
Desde el punto de vista de la implementación, es útil almacenar el estado de la programación dinámica y los indicadores de cada publicación en forma empaquetada en un número entero para acelerar el trabajo del programa (ver código), y no en una lista o tupla. Esta solución usa menos memoria y le permite actualizar efectivamente el estado de la dinámica.
Código de solución completa:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2 Aproximación de funciones
Condición
Para evaluar el grado de relevancia de los documentos, se utilizan varios métodos de aprendizaje automático, por ejemplo, árboles de decisión. El árbol de decisión k-ary tiene una regla de decisión en cada nodo que divide los objetos en k clases según los valores de algún atributo. En la práctica, generalmente se usan árboles de decisión binarios. Considere una versión simplificada del problema de optimización, que debe resolverse en cada nodo del árbol de decisión k-ary.
Deje que una función discreta f se defina en los puntos i = 1, 2, ..., n. Es necesario encontrar una función constante por partes g que consista en no más de k secciones de constancia de modo que el valor SSE =
(g (i) - f (i))
2 es mínimo.
Formatos de E / S y ejemplosFormato de entrada
La primera línea contiene dos enteros n y k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
La segunda línea contiene n enteros f (1), f (2), ..., f (n): los valores de la función aproximada en los puntos 1, 2, ..., n (–10
6 ≤ f (i) ≤ 10
6 ).
Formato de salida
Imprima un solo número: el valor mínimo posible de SSE. La respuesta se considera correcta si el error absoluto o relativo no excede de 10 a
6 .
Ejemplo 1
Ejemplo 2
Ejemplo 3
Notas
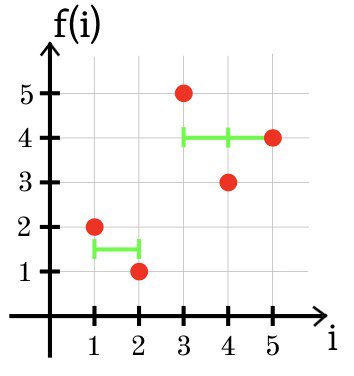
En el primer ejemplo, la función óptima g es la constante g (i) = 2.
SSE = (2 - 1)
2 + (2 - 2)
2 + (2 - 3)
2 = 2.
En el segundo ejemplo, hay 2 opciones. O g (1) = 1 yg (2) = g (3) = 2.5, o g (1) = g (2) = 1.5 y
g (3) = 3. En cualquier caso, SSE = 0.5.
En el tercer ejemplo, la aproximación óptima de la función f usando dos secciones de constancia se muestra a continuación: g (1) = g (2) = 1.5 y g (3) = g (4) = g (5) = 4.
SSE = (1.5 + 2)
2 + (1.5 - 1)
2 + (4 - 5)
2 + (4 - 3)
2 + (4 - 4)
2 = 2.5.
Sistema de calificación
Las pruebas para esta tarea consisten en cinco grupos. Los puntos para cada grupo se otorgan solo al pasar todas las pruebas del grupo y todas las pruebas de grupos
anteriores . Pasar las pruebas de las condiciones es necesario para obtener puntos para los grupos a partir de la segunda. En total para la tarea puede obtener
100 puntos .
En el sistema de prueba, las pruebas 1-3 son ejemplos de la condición.
1.
(10 puntos) pruebas 4–22: k = 1, no se requieren pruebas de la condición
2.
(20 puntos) pruebas 23–28: k ≤ 2
3.
(20 puntos) pruebas 29–34: k ≤ 3
4.
(20 puntos) pruebas 35–40: k ≤ 4
5.
(30 puntos) pruebas 41–46: sin restricciones adicionales
Solución
Como sabe, la constante que minimiza el valor SSE para un conjunto de valores f
1 , f
2 , ..., f
n es el promedio de los valores enumerados aquí. Además, como es fácil de verificar mediante cálculos simples, el valor SSE =
.
La decisión es de 10 puntos : simplemente consideramos el promedio de todos los valores de la función y SSE como O (n).
La decisión es de 30 puntos : clasificamos el último punto relacionado con la primera parte de la constancia de los dos, para una partición fija calculamos el SSE y seleccionamos el óptimo. Además, es importante no olvidar desmontar el caso cuando solo hay una sección de permanencia. Dificultad - O (n
2 ).
La decisión es de 50 puntos : clasificamos los límites de la división en secciones de constancia para O (n
2 ), para una partición fija en 3 segmentos, calculamos el SSE y elegimos el óptimo. Dificultad - O (n
3 ).
La decisión es de 70 puntos : calculamos las sumas y sumas de cuadrados de los valores de f
i en los prefijos, esto le permitirá calcular rápidamente el promedio y la ESS en cualquier segmento. Ordenamos los límites de la partición en 4 secciones de constancia para O (n
3 ), usando los valores precalculados en los prefijos para O (1), calculamos el SSE. Dificultad - O (n
3 ).
Solución completa : considere la función de programación dinámica dp [s] [i]. Este es el valor SSE más pequeño si aproximamos los primeros valores i usando segmentos s. Entonces
dp [0] [0] = 0, y para todos los demás conjuntos de parámetros, establecemos el valor igual al infinito para minimizar aún más este valor. Resolveremos el problema, aumentando gradualmente el valor de s. ¿Cómo calcular dp [s] [i] si los valores dinámicos para todos los s más pequeños ya están calculados? Es suficiente designar para t el número de primeros puntos cubiertos por los segmentos anteriores (s - 1), y ordenar todos los valores de t, y aproximar los puntos restantes (i - t) usando el segmento restante. Es necesario elegir el mejor valor t para el SSE final en i puntos. Si calculamos las sumas y sumas de cuadrados de los valores de f
i en los prefijos, entonces esta aproximación se realizará en O (1), y el valor dp [s] [i] se puede calcular en O (n). La respuesta final es dp [k] [n]. La complejidad total del algoritmo es O (kn
2 ).
Código de solución completa:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C. Predicción de clics de usuario
Condición
Una de las señales más importantes para un sistema de recomendación es el comportamiento del usuario. , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/train.csv:
test.csv:
:
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) , . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
( ), , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .