Capa convolucional: convolución rápida según el método de Shmuel Vinograd

Introduccion

Este artículo es una continuación de una serie de artículos que describen los algoritmos subyacentes.
Synet es un marco para lanzar redes neuronales pre-entrenadas en la CPU.

En un artículo anterior , describí métodos basados ​​en la multiplicación de matrices. Estos métodos con un esfuerzo mínimo pueden lograr en muchos casos más del 80% del máximo teórico. Parecería, bueno, ¿dónde podemos mejorarlo más? Resulta que puedes! Existen métodos matemáticos que pueden reducir la cantidad de operaciones requeridas para la convolución. Nos familiarizaremos con uno de estos métodos, el algoritmo de convolución por el método de Vinograd, en este artículo.


Shmuel Winograd 1936.01.04 - 2019.03.25 - Un destacado científico informático israelí y estadounidense, creador de algoritmos para la multiplicación matricial rápida, convolución y transformación de Fourier.

Un poco de matemática

Aunque, en el aprendizaje automático, las convoluciones con un núcleo cuadrado se usan con mayor frecuencia, para simplificar la presentación, primero consideramos el caso unidimensional. Supongamos que tenemos una imagen de tamaño unidimensional de entrada $$$1 \ veces4$ :

$$

$$d = \ begin {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T,$$

y tamaño de filtro $$$1 \ veces3$ :

$$

$$g = \ begin {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

entonces el resultado de la convolución será:

$$

$$F (2,3) = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}. $$$

Estas expresiones se reescribirán convenientemente en forma de matriz:

$$

$$F (2,3) = \ begin {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ begin {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ begin {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}, (1)$$

donde se usa la notación:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2.$$

A primera vista, el último reemplazo parece algo inútil: claramente hay más operaciones. Pero las expresiones $$$\ frac {g_0 + g_1 + g_2} {2}$ y $$$\ frac {g_0-g_1 + g_2} {2}$ solo necesita ser calculado una vez. Con esto en mente, necesitamos realizar solo 4 operaciones de multiplicación, mientras que en la fórmula original deben realizarse 6.
Reescribimos la expresión (1):

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

donde $$$\ odot$ denota multiplicación por elementos, y también se usa la siguiente notación:

$$

$$B ^ T = \ begin {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}, (3) \\ G = \ begin {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}, (4) \\ A ^ T = \ comenzar {bmatrix} 1 y 1 y 1 y 0 \\ 0 y 1 y -1 y -1 \ end {bmatrix}. (5)$$

La expresión (2) se puede generalizar al caso bidimensional:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

El número requerido de operaciones de multiplicación para $$$F (2 \ veces2,3 \ veces3)$ encogerse de $$$2 \ times2 \ times3 \ times3 = 36$ antes $$$4 \ times4 = 16$ . Así obtenemos la ganancia computacional en $$$\ frac {36} {16} = $ 2.2$ tiempos Si visualiza, de hecho, en lugar de calcular por separado la convolución para cada punto de la imagen, la calcularemos inmediatamente para un bloque de tamaño $$$2 \ veces2$ :

En cualquier caso, por convolución con la ventana $$$r \ veces s$ y tamaño de bloque $$$m \ veces n$ el número de multiplicaciones requeridas será

$$

$$cuenta = (m + r - 1) \ veces (n + s - 1), (7)$$

y la ganancia se describe mediante la fórmula:

$$

$$k = \ frac {m \ veces n \ veces r \ veces s} {(m + r - 1) \ veces (n + s - 1)}. (8)$$

En el límite, para lo suficientemente grande $$$m$ y $$$n$ para cualquier convolución, ¡solo 1 operación de multiplicación por punto es suficiente! Desafortunadamente, un aumento en el tamaño del bloque conduce a un rápido aumento en la sobrecarga de entrada $$$B ^ T d B$ y fin de semana $$$A ^ T [...] A$ imágenes, por lo que, en la práctica, generalmente no se utiliza un tamaño de bloque mayor $$$4 \ veces4$ .

Ejemplo de implementación

Para la implementación práctica del algoritmo de Vinograd, me gustaría considerar el caso más simple: convolución con el núcleo $$$3 \ veces3$ para bloque $$$2 \ veces2$ . Para simplificar aún más la presentación, también asumiremos que no hay relleno de la imagen de entrada, y los tamaños de las imágenes de entrada y salida son múltiplos de 2.

La implementación de convolución basada en la multiplicación de matrices se verá así:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Aquellos que quieran entender en detalle lo que está sucediendo aquí deberían consultar mi artículo anterior . La implementación actual se obtiene de la anterior, si ponemos:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

Algoritmo de convolución modificado

Doy aquí nuevamente la fórmula (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

Si cambia del tamaño de la imagen de salida $$$2 \ veces2$ a una imagen de tamaño arbitrario, entonces tendremos que dividirla en bloques de tamaño $$$2 \ veces2$ . Para cada uno de esos bloques, se formará una imagen de entrada $$$(2 + 3 - 1) \ veces (2 + 3 - 1) = $ 1$ valores incluidos en 16 convertidos $$$B ^ T d B$ imágenes de entrada reducidas a la mitad. Luego, cada una de estas 16 matrices se multiplica por la matriz correspondiente de los pesos transformados $$$G g G ^ T$ . 16 matrices resultantes se convierten a la imagen de salida $$$A ^ T \ bigg [... \ bigg] A$ . Debajo de este proceso se dibuja en el diagrama:



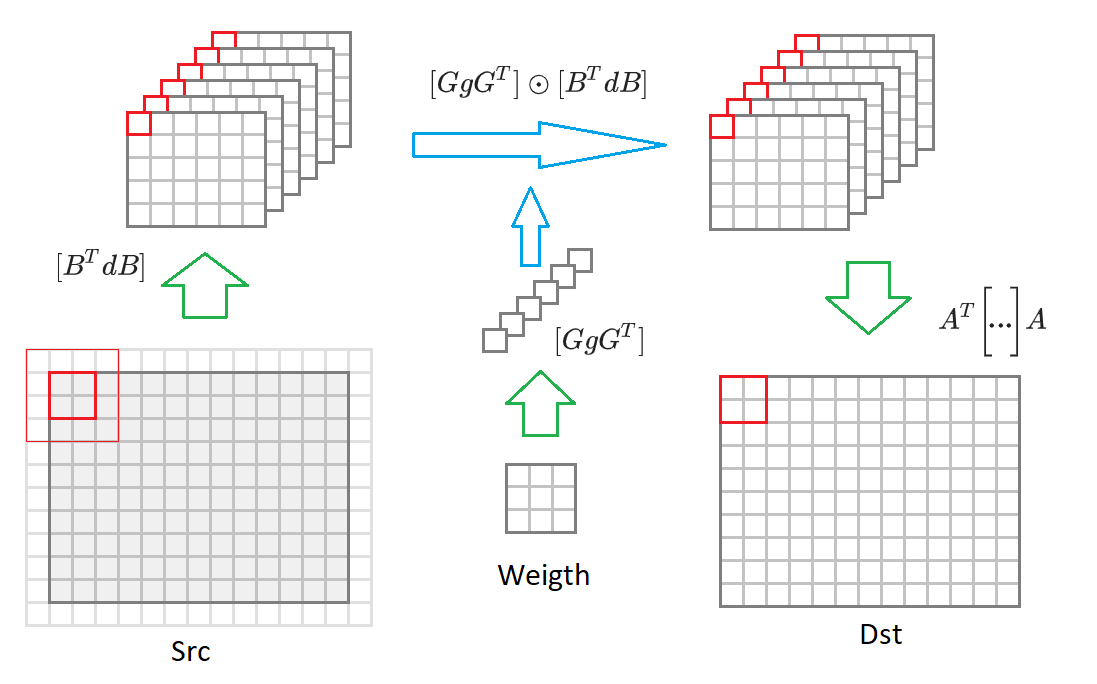
Dados estos comentarios, el algoritmo de convolución toma la forma:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

El número de operaciones que se requieren sin tener en cuenta las transformaciones de la imagen de entrada y salida: ~ srcC * dstC * dstH * dstW * count . A continuación, describimos los algoritmos para convertir pesos, imágenes de entrada y salida.

Convertir escalas convolucionales

Como se puede ver en la expresión (6), la siguiente transformación debe realizarse en pesos de convolución: $$$G g G ^ T$ donde esta la matriz $$$G$ definido en la expresión (4). El código para esta conversión se verá así:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

Afortunadamente, esta conversión debe hacerse solo 1 vez. Por lo tanto, no afecta el rendimiento final.

Conversión de imagen de entrada

Como se puede ver en la expresión (6), la siguiente transformación debe realizarse en la imagen de entrada: $$$B ^ T d B$ donde esta la matriz $$$B ^ T$ definido en la expresión (3). El código para esta conversión se verá así:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

El número de operaciones requeridas para esta conversión es: ~ srcH * srcW * srcC * count .

Conversión de imagen de salida

Como se puede ver en la expresión (6), la siguiente transformación se debe realizar en la imagen de salida: $$$A ^ T [...] A$ donde esta la matriz $$$B ^ T$ definido en la expresión (5). El código para esta conversión se verá así:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

El número de operaciones requeridas para esta conversión es: ~ dstH * dstW * dstC * count .

Características de implementación práctica

En el ejemplo anterior, describimos el algoritmo de Vinohrad para un bloque de tamaño $$$2 \ veces2$ . En la práctica, una versión más avanzada del algoritmo se usa con mayor frecuencia: $$$F (4 \ veces4,3 \ veces3)$ . En este caso, el tamaño del bloque será $$$4 \ veces4$ , y el número de matrices transformadas es 36. La ganancia computacional, según la fórmula (8), alcanzará 4 . El esquema general del algoritmo es el mismo, solo difieren la matriz de algoritmos de transformación.

Hay un pequeño proyecto en Github que le permite calcular estas matrices con coeficientes para un tamaño de núcleo de convolución arbitraria y tamaño de bloque.

Presentamos una variante del algoritmo de Vinograd para el formato de imagen NCHW , pero el algoritmo se puede implementar de manera similar para el formato NHWC (en el artículo anterior hablé con más detalle sobre estos formatos de imagen).

A pesar de la presencia de transformaciones adicionales, la carga computacional principal en el algoritmo de Vinograd (con su aplicación competente, por supuesto) todavía reside en la multiplicación de matrices. Afortunadamente, esta es una operación estándar y se implementa efectivamente en muchas bibliotecas.

Las funciones de transformación optimizadas para diferentes plataformas para el algoritmo de Vinohrad se pueden encontrar aquí .

Pros y contras del algoritmo de uva

Primero, por supuesto, los pros:

• El algoritmo permite varias veces (la mayoría de las veces, 2-3 veces) acelerar el cálculo de la convolución. Por lo tanto, es posible calcular la convolución más rápido que el límite "teórico".
• El algoritmo se basa en su implementación en el algoritmo de multiplicación matricial estándar.
• Se puede implementar para varios formatos de imagen de entrada: NCHW , NHWC .
• El tamaño del búfer para almacenar valores intermedios es menor que el requerido para el algoritmo de multiplicación de matrices.

Bueno y donde sin inconvenientes:

• El algoritmo requiere una implementación separada de las funciones de conversión para cada tamaño de núcleo de convolución, así como para cada tamaño de bloque. Tal vez esta sea una de las principales razones por las que se implementa en casi todas partes solo por convolución con el núcleo. $$$3 \ veces3$ .
• A medida que aumenta el tamaño del bloque, la complejidad de implementar funciones de conversión crece rápidamente. Por lo tanto, prácticamente no hay implementaciones con un tamaño de bloque mayor que $$$4 \ veces4$ .
• El algoritmo impone restricciones estrictas a los parámetros de convolución strideY = strideY = dilationY = dilationX = group = 1 . Aunque teóricamente, es posible implementar el algoritmo cuando se violan estas restricciones, en la práctica es pequeño debido a su baja eficiencia.
• La eficiencia del algoritmo disminuye si el número de canales de entrada o salida en la imagen es pequeño (esto se debe al costo de convertir las imágenes de entrada y salida).
• La eficiencia del algoritmo disminuye para tamaños pequeños de imágenes de entrada (las matrices resultantes de la imagen de entrada son demasiado pequeñas, y el algoritmo de multiplicación de matriz estándar se vuelve ineficaz para ellas).

Conclusiones

El método de cálculo de convolución basado en el algoritmo de Vinograd puede aumentar significativamente la eficiencia computacional en comparación con el método basado en la multiplicación de matriz simple. Desafortunadamente, no es universal y es bastante difícil de implementar. Para una serie de casos especiales, hay enfoques más rápidos, cuya descripción me gustaría posponer para los próximos artículos de esta serie . Esperando comentarios y comentarios de los lectores. ¡Espero que te haya interesado!

PD: Este y otros enfoques son implementados por mí en el Marco de Convolución como parte de la biblioteca Simd .
Este marco subyace a Synet , un marco para ejecutar redes neuronales pre-entrenadas en la CPU.