Imagine que está rodeado por un muro infinitamente alto, pero no se sabe absolutamente nada sobre lo que hay detrás del muro. Ahora imagine que la personificación de este muro es esta ecuación:
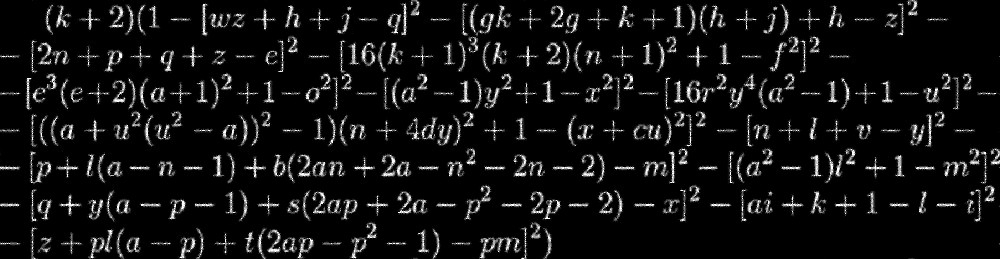
Esta metáfora será más fácil de entender si hacemos una analogía con un agujero negro: no sabemos qué hay debajo de su horizonte de eventos, y para descubrir que necesitamos encontrar una forma de llegar allí. Algo similar existe en el mundo de las matemáticas. Esta ecuación es una "fórmula" real de un número primo, pero para usarla, necesitamos descubrir cómo buscar
{a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, w, v, x, y, z} .
El agujero negro y esta ecuación son los estados finales de algo real y abstracto. Y, si hay suficientes conjeturas e ideas sobre el primero, sobre el segundo, prácticamente no se sabe nada. Pero, ¿qué pasa si es realmente un agujero negro "matemático"? ¿No tienes curiosidad por lo que puede pasar si caemos por debajo del horizonte?
¿En qué consiste el muro?
Números: no están en el mundo real. Hay siete dados, siete átomos, siete pecados capitales, pero el siete en sí no existe, es una abstracción. Sí, podríamos decir que los números son solo muchos objetos abstractos, sin embargo, este es un mundo entero. Un mundo en el que, como en el mundo real, hay leyes. La sola idea de esto parece muy extraña. Sin embargo, la existencia de una rama de las matemáticas como la teoría de números sugiere que esta "rareza" es muy importante para nosotros.
Lo más emocionante es que entre estos objetos imaginarios hay unos especiales: números primos. Son como un caos determinista: predecible e impredecible al mismo tiempo, dependiendo de la escala de su consideración. Por ejemplo, al estar junto a ellos, podemos notar que su número delante de algún número arbitrario n no excederá:
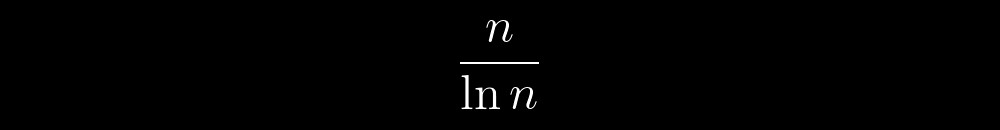
Al cambiar la escala, comenzamos a notar muchos indicios de algún tipo de reglas internas de su comportamiento. Gradualmente, estas pistas se vuelven demasiadas. Cada vez más a menudo las preguntas "¿De dónde vienen?", "¿Qué pasa si hay un cierto algoritmo para obtener números primos?", "¿Qué pasa si cada número primo se puede obtener usando el mismo algoritmo?"
Como apareció la pared
Si se obtiene una cierta secuencia de números como resultado de la operación de un cierto algoritmo, entonces el conjunto de números en esta secuencia se considera enumerable, aunque puede ser infinitamente grande. Los conjuntos enumerados tienen una propiedad notable: la diofantina. Esto significa que cualquier conjunto de este tipo puede representarse mediante una ecuación diofantina, un polinomio con coeficientes y potencias enteros positivos.
La siguiente declaración puede parecer completamente inverosímil, pero en base a esta definición, podemos argumentar que todas las claves de seguridad y los valores de las funciones hash (incluso bitcoins) se pueden expresar a través de ecuaciones de diofantina. es decir ecuaciones que se resuelven en enteros. Y sí, teóricamente, alguien puede aprender cualquier secreto, ser una persona infinitamente rica y poderosa. Pero, para convertirse en una persona así, estas ecuaciones primero deben deducirse y luego resolverse.
La computadora puede hacer frente a la tarea de representar el conjunto mediante la ecuación diofantina, parcial o completamente. Pero aquí surge otro problema: las ecuaciones de Diophantine no se resuelven de forma general, es decir No existe un algoritmo único para resolverlos. Esto no parece ser un gran problema, porque sabemos que algunas ecuaciones se distinguen en formas separadas, para cuya solución ya se han encontrado métodos efectivos.
Pero incluso a pesar de la presencia de estos métodos, inevitablemente encontramos dificultades computacionales asociadas con la precisión de los cálculos o con la velocidad de las iteraciones.
¿Cómo sucedió que los números primos eran enumerables? El proceso mismo de crear ecuaciones que representan conjuntos enumerables se basa en los fundamentos de las matemáticas: aritmética y lógica. Y si tenemos suficiente conocimiento sobre las propiedades de los objetos de un determinado conjunto, entonces, en base a este conocimiento, podemos hacer suposiciones sobre el algoritmo que permite que se obtengan. Y, como resultó, el conocimiento sobre las propiedades de los números primos se acumuló lo suficiente para este propósito. Se ha obtenido la ecuación, y ahora todas las preguntas relacionadas con los números primos se reducen solo a ella.
Pero no podemos resolverlo.
Espesor de pared y resistencia
De hecho, somos desafiados. Y sabemos de antemano sobre la inevitable derrota. Quizás un retiro sería la decisión más prudente. ¿Pero no necesitamos estas derrotas para superarnos? Tratemos de resolverlo solo un poco.
Echa un vistazo a la ecuación de nuevo:
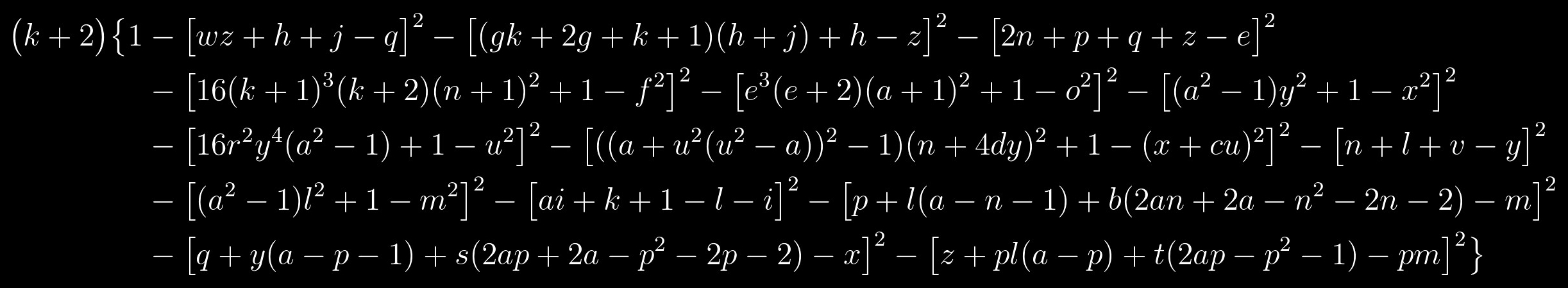
Este es un polinomio cuyo conjunto de valores positivos coincide con el conjunto de primos. Consiste en dos factores: el factor izquierdo será primo solo cuando el factor derecho, indicado entre corchetes, es igual a uno, y esto, a su vez, es posible solo si cada término en este factor, indicado entre corchetes, es igual a cero . Resulta que la cuestión de resolver esta ecuación se reduce a resolver un sistema de las siguientes ecuaciones:
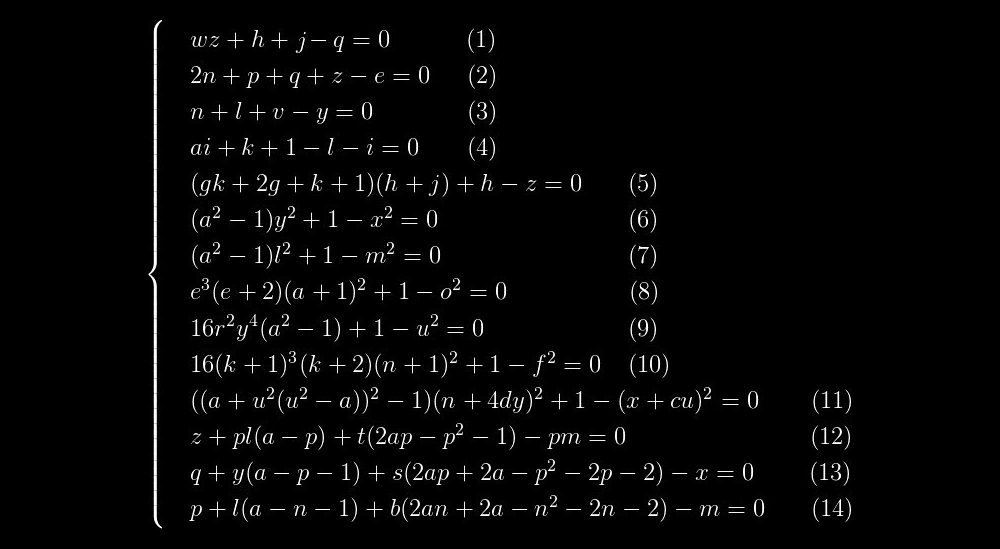
Si resolvemos este sistema de ecuaciones y sumamos 2 al valor encontrado de
k , obtenemos un número primo. Pero podemos ir hacia otro lado. Tome un número primo, reste 2 de él, obteniendo así el valor de
k , luego sustitúyalo en el sistema e intente encontrar los valores de las variables restantes en relación con él. Es así como iremos: intente encontrar al menos una solución para este polinomio.
Todas las variables están sujetas a dos restricciones estrictas; deben ser enteras y no pueden ser negativas. Si tomamos
k = 0 , entonces el primer número primo que podemos obtener es 2. Este será nuestro punto de partida. Después de sustituir este valor en el sistema de ecuaciones, tomará la siguiente forma:
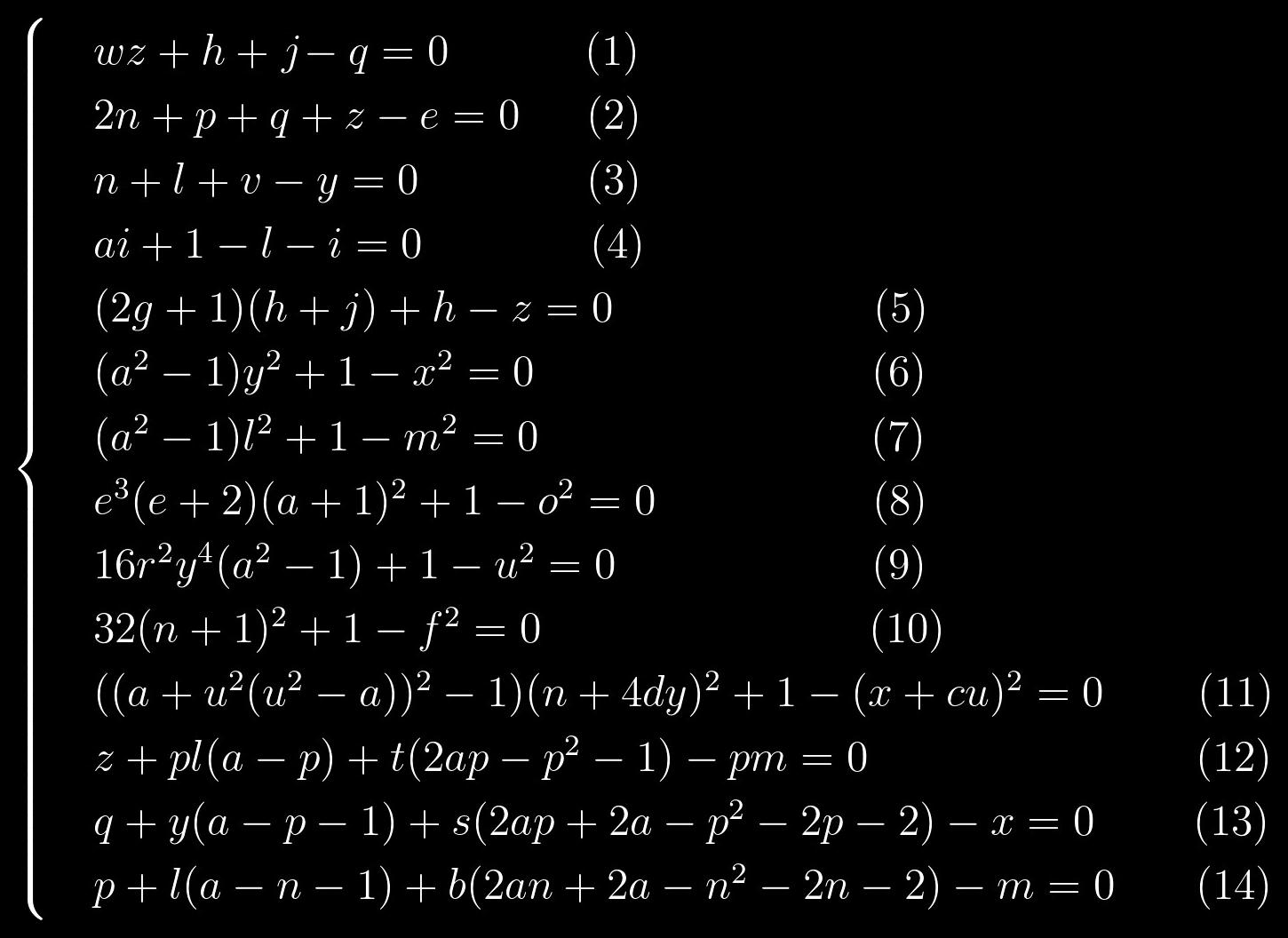
Las ecuaciones (1) - (5) son ecuaciones lineales, es decir los grados de todas las variables son 1. Las ecuaciones (6) - (11) tienen una estructura muy similar. Y finalmente, las ecuaciones (12) - (14) también se destacan en un grupo separado, y las ecuaciones (13) y (14) son similares entre sí, como dos gotas de agua.
Podemos deshacernos de las variables, o bajar el grado, pero ya lo hemos hecho antes. Una disminución en el número de variables conduce a un fuerte aumento en los grados de otras variables, y una disminución en los grados de variables solo es posible a través de un aumento en su número. Así que tratemos de resolver este sistema de esta forma.
Las ecuaciones (6) - (11) son modificaciones de la ecuación de Pell:
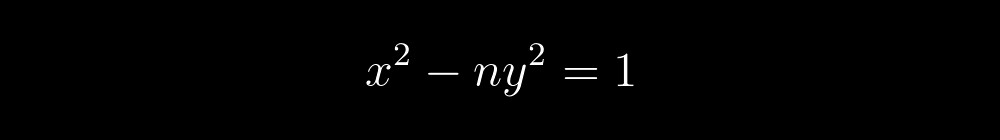
De hecho, si los reescribe así:
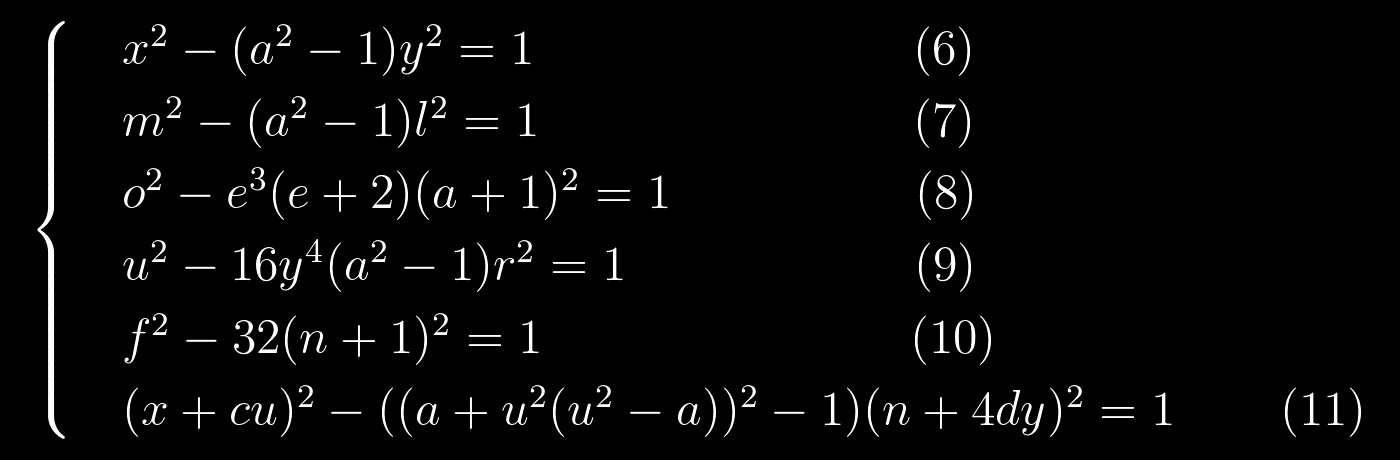
entonces la similitud se hace evidente. Esto es muy alentador, ya que podemos resolver las ecuaciones de Pell bastante bien. Podemos intentar resolver este sistema así: primero resolvemos una ecuación, sustituimos sus soluciones en otra, que también resolvemos, y así sucesivamente hasta el final. Suena bastante simple, pero no estaría de más dibujar algo así como un gráfico de permutación para saber al menos aproximadamente en qué orden resolver las ecuaciones:
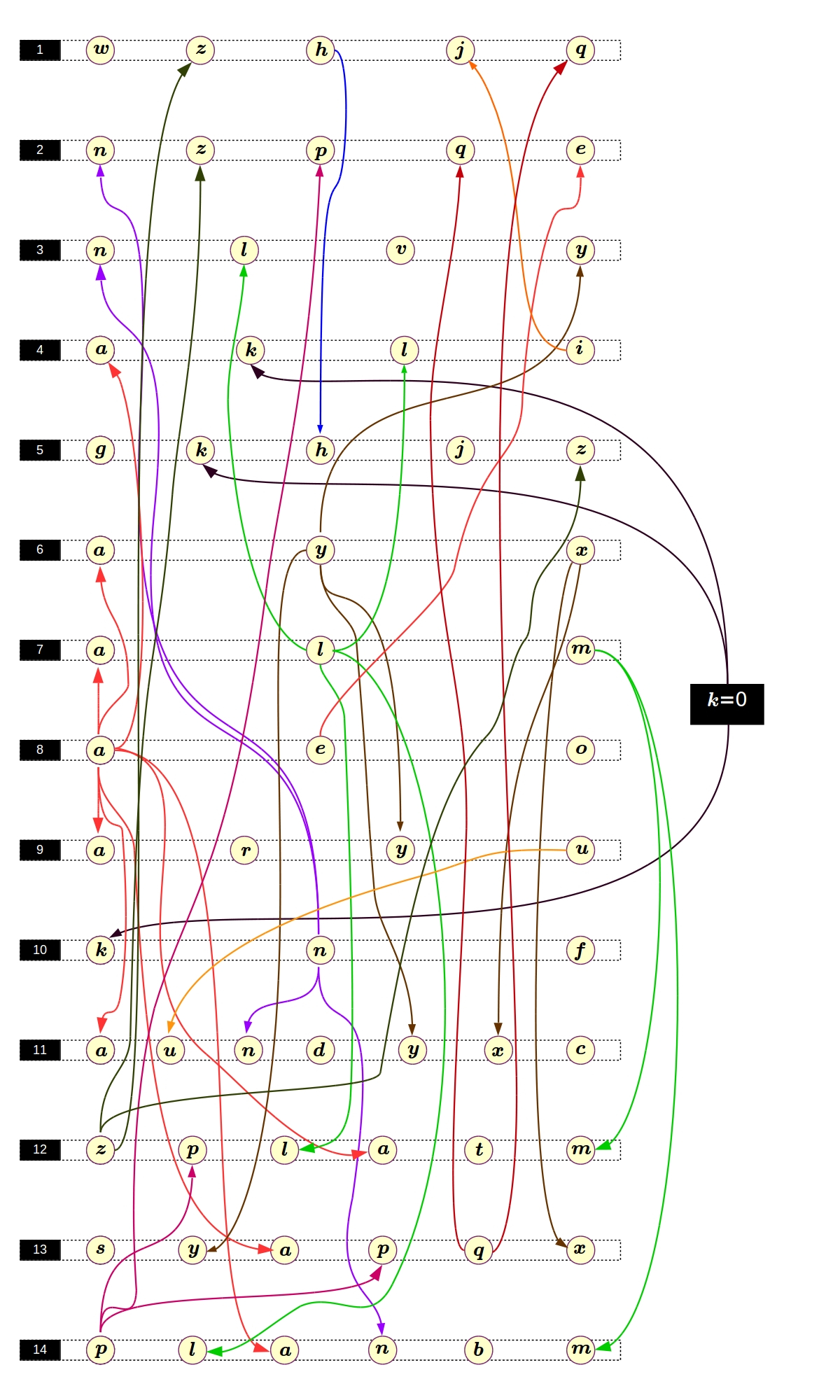
Parece que todo es simple.
Patear la pared
Comenzamos con las ecuaciones de Pell. Para resolverlos, escribiremos un pequeño script:
from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i
Gracias a él, podemos encontrar inmediatamente una solución a la ecuación (10)
n = 2 ,
f = 17 . Sin embargo, antes de continuar, necesitamos saber algo sobre la ecuación de Pell.
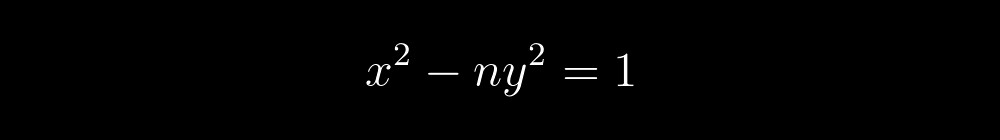
Para empezar,
n no puede ser un cuadrado completo. Además, cualquier ecuación de Pell tiene un número infinito de soluciones, entre las cuales siempre hay una trivial:
x = 1 e
y = 0 . Cada decisión posterior se puede obtener sobre la base de las anteriores, de acuerdo con la siguiente fórmula de recurrencia:
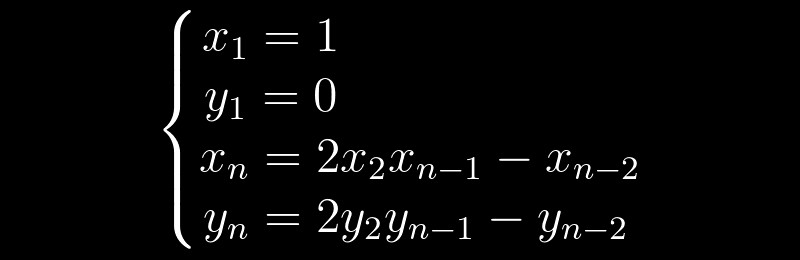
Resulta que es suficiente para nosotros encontrar la solución mínima no trivial, y podemos obtener todo lo demás usando un algoritmo simple. Por ejemplo, para
n = 2, podemos encontrar fácilmente tal solución, es
x = 3 e
y = 2 , luego las soluciones posteriores se verán así:
17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048
¿Vale la pena continuar con la decisión adicional? Por supuesto que vale la pena, pero ... podemos intentar predecir lo que nos espera.
Imaginemos por ahora que estamos resolviendo un sistema de ecuaciones de tres ecuaciones de Pell de la siguiente forma:
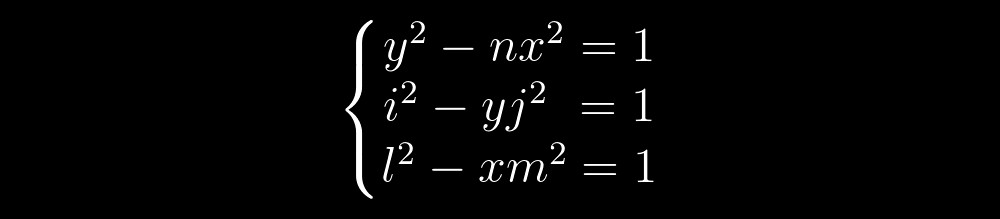
La solución a cualquier ecuación de Pell son los puntos de hipérbola con coordenadas enteras. Entonces, podemos imaginar una solución a las dos primeras ecuaciones como esta:
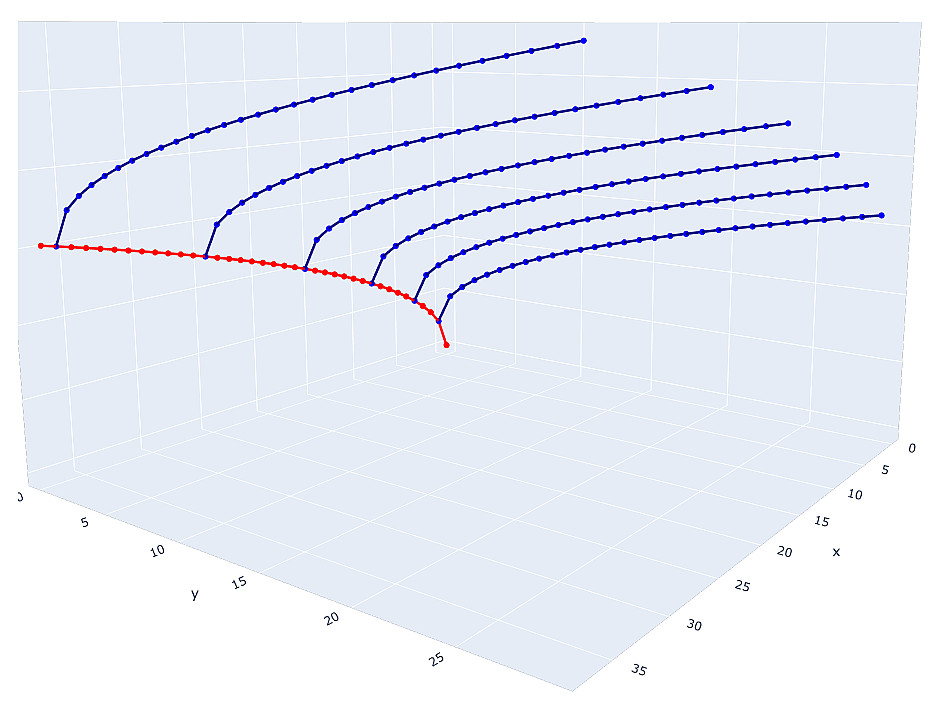
La solución a la primera ecuación son los puntos enteros de la hipérbola roja, pero la coordenada
y de cada punto está presente en la segunda ecuación y puede generar cualquier hipérbola azul cuyos puntos enteros serán la solución a la segunda ecuación.
Incluso este diagrama esquemático es suficiente para comprender que estamos tratando con un gran número de posibles candidatos para resolver el sistema. ¿Por qué candidatos? Debido a que algunos puntos enteros de la hipérbola serán necesariamente cuadrados completos, es decir soluciones inapropiadas Y si imagina que se imponen condiciones adicionales a cada variable en el sistema, encontrar candidatos para una solución será extremadamente difícil. Y hasta ahora solo estamos hablando de un sistema de tres ecuaciones.
Pero volvamos a nuestra "fórmula" de números primos. ¿Qué puede estar delante de nosotros?
Tarde o temprano, descubriremos que el parámetro
n en la ecuación de Pell se volverá catastróficamente grande. El método de fracciones continuas se volverá simplemente inútil. Definitivamente intentaremos algo más, por ejemplo, enumerar valores con tamizado, generalizar de alguna manera todo el proceso y llegar a algoritmos como un tamiz cuadrático o un tamiz de un campo numérico. Al final, nos centraremos en el método "chakraval", aunque también experimentará algunas dificultades.
En cierto momento, sentiremos cierta confianza en la solución de cada ecuación individual del sistema. Pero no todo el sistema. Intentaremos aplicar algunos métodos de optimización heurística, por ejemplo, un algoritmo de recocido o un algoritmo de hormiga. Pero aquí fallaremos. Para comprender al menos de alguna manera las razones de estas fallas, tendremos que sumergirnos un poco en la geometría y la topología algebraica. Poco a poco, tendremos una idea de la "sustancia cristalizable". Podemos imaginar remotamente la estructura de la hiperesuperficie sobre la cual liberamos hormigas.
En base a estas ideas, intentaremos mejorar nuestros algoritmos. Para hacer esto, tomaremos los mejores logros de muchas ramas de las matemáticas. Gradualmente, habrá menos posibilidades en los algoritmos, pero aún así no puede deshacerse de ellos. ¿Qué pasará después? De repente, encontramos que muchos candidatos adecuados para una verdadera decisión en algunos lugares son paradójicamente densos. Cada una de esas densidades dará esperanza de que en algún lugar de su centro se oculte la respuesta oculta. Tales densidades "parecerán" a las hormigas como algo así como un hiperfunnel invertido. Intentaremos "golpear" sus centros y sus máximos. Pero entonces, ¿qué pasará?
¿Qué hay detrás de la pared?
Probablemente no sé cómo, pero resolveremos esta ecuación. Tal vez las computadoras cuánticas o (!) Quark nos ayudarán. Pero esto no se convertirá en un agujero en la pared. Probablemente, los primos gaussianos y una ecuación aún más complicada que representará a muchos de ellos nos esperarán más. Entonces, quizás, entre otros números hipercomplejos, volveremos a encontrar algún tipo de comportamiento "simple". Tal vez esto, al final, sea el límite, una especie de horizonte de eventos para un agujero negro matemático.
¿Qué podría haber bajo este horizonte? Probablemente algún tipo de singularidad matemática. Probablemente, sabremos absolutamente todo acerca de todos los conjuntos, podremos resolver cualquier ecuación y cualquier problema. ¿O tal vez no habrá más preguntas y tareas nuevas?
Son precisamente esos pensamientos los que surgen. Bueno, de hecho, haga cualquier pregunta sobre números primos y gracias a esta ecuación puede obtener una respuesta. ¿El número de primos gemelos es infinito? Resuelve esta ecuación, haz un par de cálculos algebraicos y obtén la respuesta. ¿Cuáles son los números primos que terminan en 1, 3, 7 o 9? El mismo algoritmo: un par de cálculos y sustitución de la ecuación. ¿Desea descomponer rápidamente los números en factores primos? ..
En conclusión
Conocí esta ecuación por primera vez en 2008, para entonces ya estaba loco por la criptografía y la teoría de números, en particular, el esquema RSA y el problema de factorización. Por supuesto, el polinomio que genera números primos me pareció un tema muy interesante, pero demasiado complicado. Sin embargo, todos los problemas que podían o no resolverse estaban de alguna manera relacionados con las ecuaciones de Diophantine. Por lo tanto, ya en 2014, volví a este polinomio, decidiendo simplemente explorar todas las secciones de las matemáticas en una fila y buscar algo que pudiera ser útil para resolverlo. Por supuesto, no se puede hablar de ninguna cultura académica de todos mis trabajos: nunca guardé registros sistemáticos, nunca agregué el código generado. Este es solo mi hobby.
La idea de escribir este artículo surgió después de que vi la película Interestelar. No podía creer que los agujeros negros y la gravedad pudieran ser representados de manera tan excitante. Pero resultó que el mundo matemático "inexistente" me proporcionó las mismas impresiones todo el tiempo. Este mundo también tiene su propio "espacio profundo" inaccesible y sus propias "partículas elementales".
Con este artículo, quería mostrar que es posible abordar al menos un poco cualquier tarea, la más difícil e incluso imposible. Hay muchas tareas de este tipo, y puede elegir una que sea de su agrado y más cercana al área de interés. Por supuesto, la complejidad excesiva y la derrota garantizada privarán al más mínimo deseo en esta empresa. Pero toda la paradoja es que los viajes y aventuras más interesantes, incluso en el mundo "inexistente" de las matemáticas, con mayor frecuencia, comienzan de esta manera.