Un estudio reciente,
"Uso y atribución de fragmentos de código de desbordamiento de pila en proyectos GitHub", de repente descubrió que la mayoría de las veces en proyectos de código abierto, mi
respuesta fue escrita hace casi diez años. Irónicamente, hay un error.
Érase una vez ...
En 2010, estaba sentado en mi oficina y haciendo tonterías: me divertí con el
código de golf y
agregué una calificación a Stack Overflow.
La siguiente pregunta me llamó la atención: ¿cómo mostrar el número de bytes en un formato legible? Es decir, cómo convertir algo como 123456789 bytes a "123.5 MB".
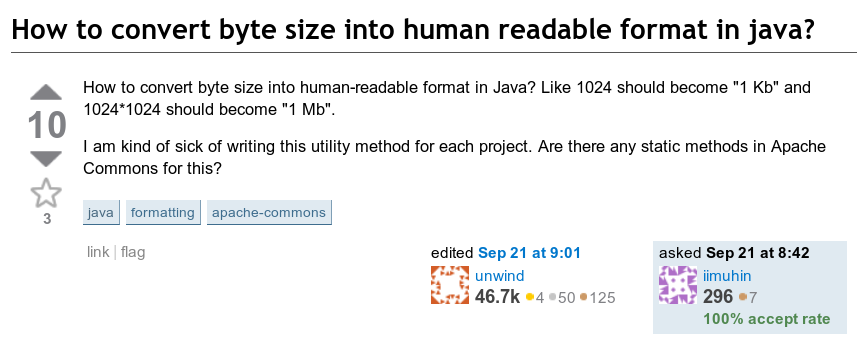Buena interfaz de 2010, gracias The Wayback MachineImplícitamente, el resultado sería un número entre 1 y 999.9 con la unidad apropiada.
Ya había una respuesta con un bucle. La idea es simple: verifique todos los grados desde la unidad más grande (EB = 10
18 bytes) hasta la más pequeña (B = 1 byte) y aplique el primero, que es menor que el número de bytes. En pseudocódigo, se ve más o menos así:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Por lo general, con la respuesta correcta con una calificación positiva, es difícil ponerse al día. En la jerga de Stack Overflow, esto se llama el
problema del tirador más rápido en Occidente . Pero aquí la respuesta tenía varios defectos, así que todavía esperaba superarla. Al menos el código con un bucle puede reducirse considerablemente.
Bueno, esto es álgebra, ¡todo es simple!
Entonces me di cuenta. Los prefijos son kilo-, mega-, giga-, ... - nada más que el grado de 1000 (o 1024 en el estándar IEC), por lo que el prefijo correcto se puede determinar utilizando el logaritmo, y no el ciclo.
Basado en esta idea, publiqué lo siguiente:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Por supuesto, esto no es muy legible, y log / pow es inferior en eficiencia a otras opciones. Pero no hay bucle y casi no hay ramificación, por lo que el resultado es bastante hermoso, en mi opinión.
La matemática es simple . El número de bytes se expresa como byteCount = 1000 s , donde s representa el grado (en notación binaria, la base es 1024). La solución s da s = log 1000 (byteCount).
No hay una expresión simple log 1000 en la API, pero podemos expresarla en términos del logaritmo natural de la siguiente manera s = log (byteCount) / log (1000). Luego, convertimos s en int, por lo que si, por ejemplo, tenemos más de un megabyte (pero no un gigabyte completo), se utilizará MB como unidad de medida.
Resulta que si s = 1, entonces la dimensión es kilobytes, si s = 2 - megabytes y así sucesivamente. Divida byteCount por 1000 sy coloque la letra correspondiente en el prefijo.
Todo lo que quedaba era esperar y ver cómo la comunidad percibía la respuesta. No podría pensar que este código se convertiría en el más difundido en la historia de Stack Overflow.
Estudio de atribución
Avance rápido hasta 2018. El estudiante graduado Sebastian Baltes publica un artículo en la revista científica
Empirical Software Engineering titulado
“Uso y atribución de fragmentos de código de desbordamiento de pila en proyectos GitHub” . El tema de su investigación es cuánto se respeta la licencia Stack Overflow CC BY-SA 3.0, es decir, ¿señalan los autores que los enlaces de Stack Overflow son una fuente de código?
Para el análisis, se extrajeron fragmentos de código del
volcado de desbordamiento de pila y se asignaron al código en los repositorios públicos de GitHub. Cita del resumen:
Presentamos los resultados de un estudio empírico a gran escala que analiza el uso y la atribución de fragmentos no triviales de código Java de respuestas SO en proyectos públicos de GitHub (GH).
(Spoiler: no, la mayoría de los programadores no cumplen con los requisitos de la licencia).
El artículo tiene una tabla de este tipo:
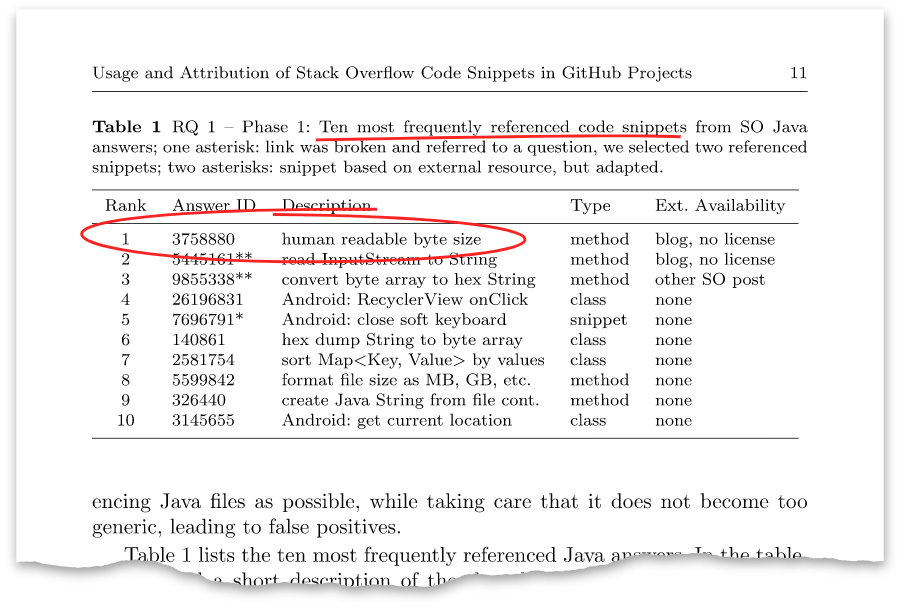
Esta respuesta anterior con el identificador
3758880 resultó ser la respuesta que
publiqué hace ocho años. Por el momento, tiene más de cien mil visitas y más de mil ventajas.
Una búsqueda rápida en GitHub realmente produce miles de repositorios con el código
humanReadableByteCount .
Busque este fragmento en su repositorio:
$ git grep humanReadableByteCount
Una historia divertida , como descubrí sobre este estudio.
Sebastian encontró una coincidencia en el repositorio de OpenJDK sin ninguna atribución, y la licencia de OpenJDK no es compatible con CC BY-SA 3.0. En la lista de correo jdk9-dev, preguntó: ¿se copia el código de desbordamiento de pila de OpenJDK o viceversa?
Lo curioso es que acabo de trabajar en Oracle, en el proyecto OpenJDK, por lo que mi antiguo colega y amigo escribió lo siguiente:
Hola
¿Por qué no preguntar al autor de esta publicación directamente en SO (aioobe)? Es miembro de OpenJDK y trabajó en Oracle cuando este código apareció en los repositorios de código fuente de OpenJDK.
Oracle se toma muy en serio estos problemas. Sé que algunos gerentes se sintieron aliviados cuando leyeron esta respuesta y encontraron al "culpable".
Entonces Sebastian me escribió para aclarar la situación, lo cual hice: este código se agregó antes de unirme a Oracle y no tengo nada que ver con el commit. Es mejor no bromear con Oracle. Unos días después de que se abrió el ticket, este código se eliminó .
Bug
Apuesto a que ya pensaste en eso. ¿Qué tipo de error en el código?
Una vez más:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Cuales son las opciones?
Después de exabytes (10
18 ) son zettabytes (10
21 ). ¿Quizás un número realmente grande irá más allá de kMGTPE? No El valor máximo es 2
63 -1 ≈ 9.2 × 10
18 , por lo que ningún valor irá más allá de los exabytes.
¿Quizás la confusión entre las unidades SI y el sistema binario? No Hubo confusión en la primera versión de la respuesta, pero se solucionó con bastante rapidez.
¿Quizás exp termina en cero, causando que charAt (exp-1) se bloquee? No tampoco. La primera declaración if cubre este caso. El valor exp siempre será al menos 1.
¿Quizás algún extraño error de redondeo en la extradición? Bueno, finalmente ...
Muchos nueves
La solución funciona hasta que se acerca a 1 MB. Cuando se especifican
"1000,0 kB" bytes como entrada, el resultado (en modo SI) es
"1000,0 kB" . Aunque 999,999 está más cerca de 1000 × 1000
1 que de 999,9 × 1000
1 , el significante 1000 está prohibido por la especificación. El resultado correcto es
"1.0 MB" .
En mi defensa, puedo decir que en el momento de escribir esto, tal error estaba en las 22 respuestas publicadas, incluidas las bibliotecas Apache Commons y Android.
¿Cómo arreglarlo? En primer lugar, observamos que el exponente (exp) debería cambiar de 'k' a 'M' tan pronto como el número de bytes esté más cerca de 1 × 1,000
2 (1 MB) que de 999.9 × 1000
1 (999.9 k ) Esto sucede en 999,950. Del mismo modo, debemos cambiar de 'M' a 'G' cuando pasamos por 999,950,000 y así sucesivamente.
Calculamos este umbral y aumentamos la
exp si los
bytes mayores:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;
Con este cambio, el código funciona bien hasta que el número de bytes se aproxima a 1 EB.
Más nueves
Al calcular 999 949 999 999 999 999 999, el código da
1000.0 PB , y el resultado correcto es
999.9 PB . Matemáticamente, el código es preciso, entonces, ¿qué pasa aquí?
Ahora nos enfrentamos a restricciones
double .
Introducción a la aritmética de coma flotante.
De acuerdo con la especificación IEEE 754, los valores de coma flotante cercanos a cero tienen una representación muy densa, mientras que los valores grandes tienen una representación muy escasa. De hecho, la mitad de todos los valores están entre -1 y 1, y cuando se trata de números grandes, un valor de tamaño Long.MAX_VALUE no significa nada. En el sentido literal.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Consulte "Bits de coma flotante" para más detalles.
El problema está representado por dos cálculos:
- División en
String.format y
- Umbral de expansión
exp
Podemos cambiar a
BigDecimal , pero es aburrido. Además, aquí también surgen problemas, porque la API estándar no tiene un logaritmo para
BigDecimal .
Reducción de valores intermedios
Para resolver el primer problema, podemos reducir el valor de
bytes al rango deseado, donde la precisión es mejor, y ajustar la
exp consecuencia. En cualquier caso, el resultado final es redondeado, por lo que no importa que descartemos los dígitos menos significativos.
if (exp > 4) { bytes /= unit; exp--; }
Configuración de bits menos significativos
Para resolver el segundo problema
, los bits menos significativos
son importantes para nosotros (99994999 ... 9 y 99995000 ... 0 deben tener diferentes grados), por lo que debemos encontrar una solución diferente.
Primero, tenga en cuenta que hay 12 valores de umbral diferentes (6 para cada modo), y solo uno de ellos conduce a un error. Un resultado incorrecto puede identificarse de forma exclusiva porque termina en D00
16 . Para que pueda arreglarlo directamente.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;
Dado que confiamos en ciertos patrones de bits en los resultados de coma flotante, utilizamos el modificador estricto fp para garantizar que el código funcione independientemente del hardware.
Valores de entrada negativos
No está claro en qué circunstancias puede tener sentido un número negativo de bytes, pero dado que Java no tiene un
long sin signo, es mejor manejar esta opción. En este momento, una entrada como
-10000 B produce
-10000 BEscribamos
absBytes :
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
La expresión es tan detallada porque
-Long.MIN_VALUE == Long.MIN_VALUE . Ahora hacemos todos los cálculos de
exp utilizando
absBytes lugar de
bytes .
Versión final
Aquí está la versión final del código, acortada y condensada en el espíritu de la versión original:
Tenga en cuenta que esto comenzó como un intento de evitar bucles y ramificaciones excesivas. Pero después de suavizar todas las situaciones de borde, el código se volvió aún menos legible que la versión original. Personalmente, no copiaría este fragmento en producción.
Para una versión actualizada de la calidad de producción, vea un artículo separado:
"Formateando el tamaño del byte en un formato legible" .
Resultados clave
- Puede haber errores en las respuestas a Stack Overflow, incluso si tienen miles de ventajas.
- Verifique todos los casos límite, especialmente en código con Stack Overflow.
- La aritmética de coma flotante es complicada.
- Asegúrese de incluir la atribución correcta al copiar el código. Alguien puede llevarte a limpiar el agua.