En casi todos los juegos de cartas después del juego necesitas barajar las cartas. Mientras barajo las cartas, siempre surge la pregunta: "¿Ya es suficiente?" Esta es una pregunta seria: no quiero pasar demasiado tiempo y jugar en un mazo cargado tampoco es divertido.

El artículo abordará la situación.

Shuffle Way

Hay formas geniales de barajar cartas, riffle shuffle, por ejemplo.

No sé cómo, y las tarjetas de cartón no se pueden barajar así, así que barajo de una manera simple, se parece a esto:

Primero, separo la parte del mazo, luego tiro la parte de esta parte al otro lado, y luego informo la parte restante. Según mis observaciones, la gente baraja las cartas exactamente de esta manera o cerca de ellas. En general, se puede dividir en un mayor número de partes, pero estos ya son detalles. En el artículo analizaremos este método aleatorio.

¿Qué es el diseño de tarjeta al azar?

Lo primero que se me ocurrió fue que es un buen diseño, cualquier tarjeta puede ser igualmente probable que esté en el primer lugar.

Pero esto no es suficiente. Por ejemplo, si cortas el mazo, divídelo en dos en un lugar aleatorio y cámbialos, entonces la primera carta puede ser cualquier posibilidad. Pero al mismo tiempo, obviamente, este es un mal diseño: después de cada carta, excepto algunas, se colocará la misma carta antes del "corte". Es decir, los jugadores recibirán cartas "correlacionadas". En el caso de un tonto, uno será golpeado, y el otro será golpeado, y esto no será accidental.

Otro enfoque para determinar un buen diseño es que en i + 1er lugar hay una tarjeta independiente de la tarjeta en el i-ésimo lugar. Puedes imaginarlo de esta manera: si miras la carta superior del mazo, no puedes adivinar qué carta será la siguiente.

Este enfoque también puede tener problemas que se resuelven considerando grandes distribuciones conjuntas, pero para el análisis actual será completamente adecuado para nosotros.

Cómo medir la "bondad" del diseño

Tomamos el mazo sobrante del juego anterior. Numeramos todas las tarjetas en orden. La mala situación es cuando después de barajar en algún lugar después de la tarjeta con el número i hay una tarjeta con el número i + 1. Por lo tanto, mediremos la proporción de cartas que están en orden después de barajar.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total 

Está claro que incluso en un mazo bien barajado, algunas cartas caerán aleatoriamente en orden. Su participación será en promedio 1 / (n-1), donde n es el número de cartas en el mazo.

Resultados

Calculamos la probabilidad de cartas consecutivas para un mazo de 52 cartas, dependiendo del número de iteraciones de mezcla.

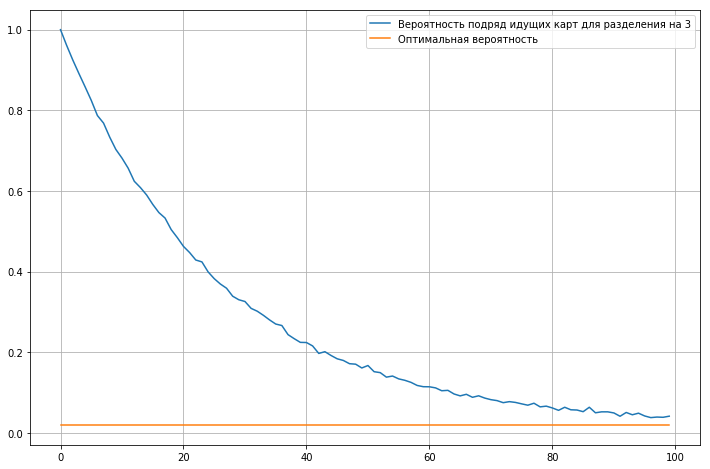
El gráfico muestra que incluso después de cientos de iteraciones, la probabilidad de tarjetas consecutivas es aproximadamente dos veces mayor que la probabilidad ideal.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend() 

En general, podemos suponer que 60 iteraciones es la cantidad óptima, menos es definitivamente malo. Hago unas 16-17 iteraciones en 30 segundos. Esto significa que para una mezcla normal , tomará casi dos minutos .

Mis amigos y yo nunca barajamos tanto las cartas. Y esto significa que nuestro juego está muy influenciado por el equilibrio del último juego.

Ten cuidado :)