Once upon a time when programming started, I often needed to draw a line of known length at an angle. And to calculate the coordinates, we used functions that take arguments in radians. I remember that in that programming environment there were no predefined constants; you could not do without remembering the number pi.
The number pi is very suitable to remember any numbers. It is well known, has practical meaning (although in practice fractions 355/113 are enough), and an unpredictable order is enough to remember and not to deduce. And it will never change.
And now we remember a couple of dozens of numbers. However, what if we urgently need to check ourselves, and next to a computer without the Internet, but with office programs? A hundred numbers are simply not stored anywhere.
But it turns out that you can build a table that calculates any number of digits (I checked up to a thousand). And it is quite simple. In general, it is now more important to remember how to make such a table, instead of remembering the numbers themselves.

The fact that such calculations are possible and an approximate calculation scheme I learned from the article
“Kranik”, or an algorithm for finding the digits of Pi . Another article.
Calculation of the Nth sign of Pi without calculating the previous ones on the topic.
We take the number of digits we need and multiply by 3.5, we get how many rows of data we need to use. Why do we multiply by 3.5? Simply, four is enough, but not three. The article “Kranik” coefficient 10/3.
Formula used
In each line there is a numerator, there is a denominator, and operating through this numerator and denominator with residues from other lines, with the formation of new residues. Dependence is both vertical and horizontal. At the top is a number. How many numbers we need, so many columns. The figure that will work out will need to be further processed, since it can be more than 9, and then you need to move the discharge forward. Accordingly, it is also necessary to accept the discharge from the next column.
We will do it in Excel. The functions used are very simple: “OSTAT” for the remainder of the division and “WHOLE” for rounding. First, the formula core is written manually on two lines, six columns. Then the formulas are stretched to the required number of rows, then we rearrange some blocks from one column to another, and then we stretch one column in breadth. We read the numbers.
So, make up the core.
The first five lines will be used to make numbers. Next, we fill in two lines of the kernel manually. The first of them, as it were, completes the calculations for a given figure, and the second can be “stretched” to all the others.
In the sixth line, write the initial numerator and denominator: A6: "0", B6: "1". For myself, I also paint them gray. In column D, enter the initial balance, which we have 2. D6: "2", D7: "2". The initial remainder I also paint in gray. Now you need to calculate the amount. C6: "= D6 * 10 + F6". And then its remainder from dividing by ten. E6: "= OSTAT (C6; 10)".
Before filling the last column of the kernel, you need to fill in the numerator and denominator of the second line. The numerator grows by 1, and the denominator grows by 2. A7: "= A6 + 1". B7: "= B6 + 2". The numerator and denominator I painted lilac. In C7, just copy from C6. It is clear that not the formula text, but the cell value. Then the reference coordinates are recounted. C7: "= D7 * 10 + F7". In cell E7, the remainder will be considered, but not modulo 10, but modulo the denominator, which is B7. E7: "= OSTAT (C7; $ B7)".
Here you need to be very careful about the $ sign. When formulas “stretch” to a range, then all its links for shifted cells are also shifted. And if we need to shift to the same column as the original column? Then the $ sign fixes the coordinate. The denominator will always be in column B, which is why it is fixed. When editing a formula, it is convenient to fix the coordinates by F4, you can press several times so that not the entire cell is fixed, but only a row or column.
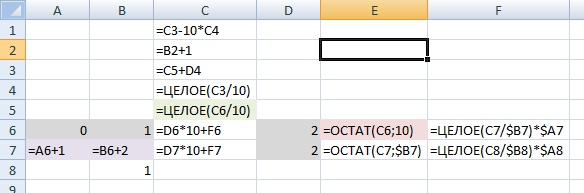
Well, now the basic formula. F6: "= WHOLE (C7 / $ B7) * $ A7".
Here, the sum of the previous line is divided by the denominator of the previous line, rounded, and multiplied by the numerator of the previous line. “Previous” - here means the previous one in the calculation order, which means that the one below. The columns for the numerator and denominator are fixed, this is required. And this formula can be moved to the second line. F7: "= WHOLE (C8 / $ B8) * $ A8".
At this stage, the main core is already there, but in the calculations it divides by zero, so for temporary convenience you need to put the unit in B8.
So, let's calculate the first digit of Pi. C5: "= WHOLE (C6 / 10)." The first digit of Pi is “2”! Do not be surprised. Simply, an unexpanded core has slightly lower accuracy than you might expect. In line 4, we will have a flag of transfer, so we recount our figure already with the transfer from the next figure. C3: "= C5 + D4". And count the new transfer. C4: "= WHOLE (C3 / 10)."
It remains to do the numbering of numbers. C2: "= B2 + 1". And the figure itself. C1: "= C3-10 * C4".
Now you can choose how many digits to get and expand the kernel. Let it be 100 digits. So, we need to expand the numerator to 350, and better to 352. I stretch the line 7. I do this: I put the cursor on A7. Shift + Ctrl + Right, Ctrl + Insert, Home, Shift + PageDown 9 times, Enter!
So that there is no division by zero, in the cell F358 we set 0. Ctrl + End, “0”, Enter. Ctrl + Home.
Now you need to transfer the blocks a couple of times.
Block D6: F358 must be moved to the left and lower, with the left column in column B. (B359: D711). Starting from cell D6: Shift + Ctrl + End, Shift + Del (or Ctrl + X), Ctrl + Down, Left, Left, Down, Shift + Ins (or Ctrl + V).
Time.
Block D359: D711 to column C. (C712: C1064) Right, Right, Ctrl + Shift + Down, Shift + Del (or Ctrl + X), Ctrl + Down, Left, Down, Shift + Ins (or Ctrl + V) .
Two.
Now column C needs to be stretched to as many columns as numbers are needed. The second line just has a counter. After stretching to column CX, the first line will contain one hundred digits of pi. Happened.