We bring the linear regression equation into matrix form

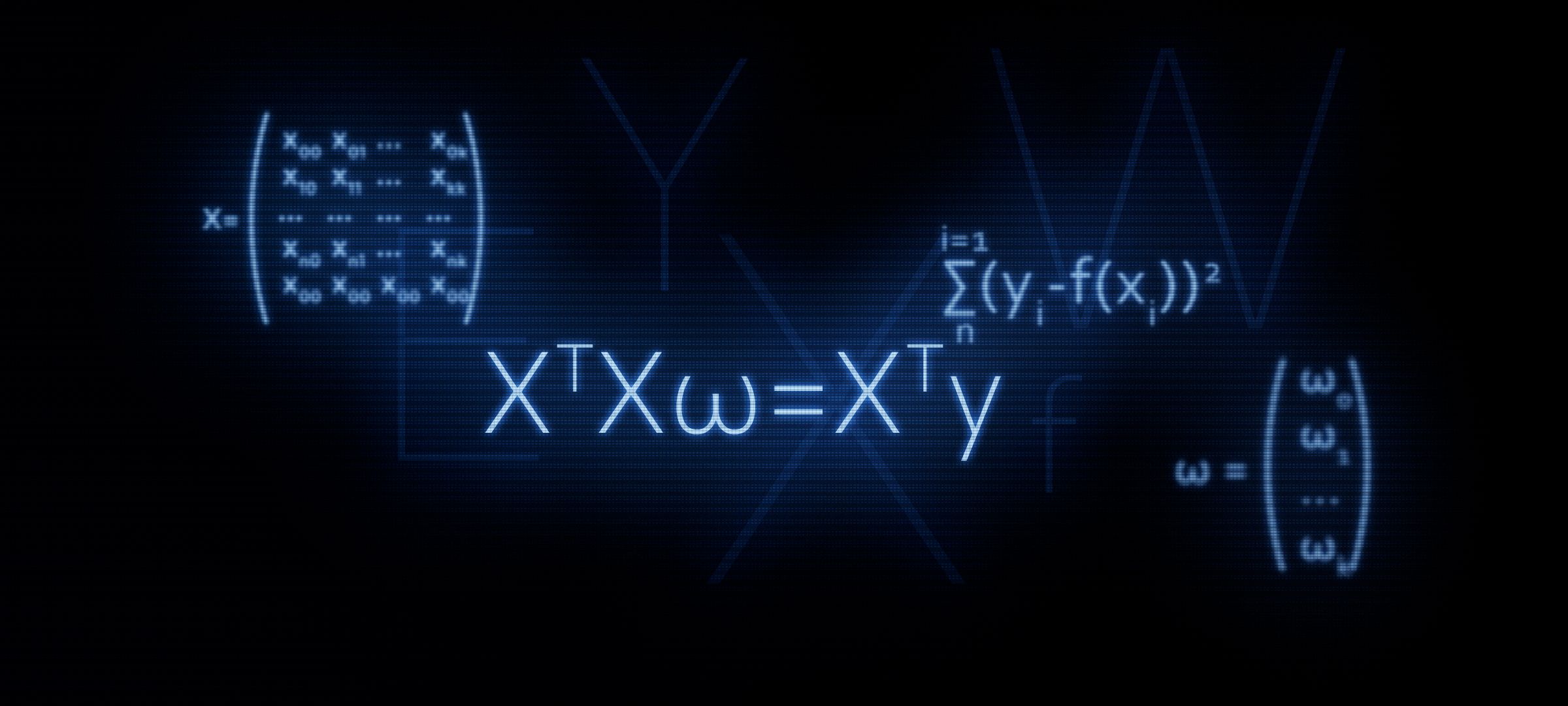
The purpose of the article is to provide support to novice datasaintists. In the previous article, we examined on the fingers three methods for solving the linear regression equation: analytical solution, gradient descent, stochastic gradient descent. Then for the analytical solution we applied the formula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ . In this article, as follows from the title, we will justify the use of this formula, or in other words, we will independently derive it.

Why it makes sense to pay increased attention to the formula $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ?

It is with the matrix equation that in most cases, acquaintance with linear regression begins. At the same time, detailed calculations of how the formula was derived are rare.

For example, at Yandex machine learning courses, when students are introduced to regularization, they suggest using the functions from the sklearn library, while not a word is mentioned about the matrix representation of the algorithm. It is at this moment that some listeners may want to understand this issue in more detail - write code without using ready-made functions. And for this, we must first present the equation with the regularizer in matrix form. This article will allow those who wish to master such skills. Let's get started.

Baseline

Targets

We have a number of target values. For example, the target may be the price of an asset: oil, gold, wheat, dollar, etc. At the same time, by a number of values ​​of the target indicator we mean the number of observations. Such observations may be, for example, monthly oil prices for the year, that is, we will have 12 target values. We begin to introduce the notation. We designate each target value as $$$y_i$ . Total we have $$$n$ observations, which means we can imagine our observations as $$$y_1, y_2, y_3 ... y_n$ .

Regressors

We assume that there are factors that to some extent explain the values ​​of the target indicator. For example, the exchange rate of the dollar / ruble pair is strongly influenced by the price of oil, the Fed rate, etc. Such factors are called regressors. At the same time, each value of the target indicator must correspond to the value of the regressor, that is, if we have 12 targets for each month in 2018, then we must also have 12 regressors for the same period. Denote the values ​​of each regressor by $$$x_i: x_1, x_2, x_3 ... x_n$ . Let in our case there is $$$k$ regressors (i.e. $$$k$ factors that influence the value of the target). So our regressors can be represented as follows: for the 1st regressor (for example, the price of oil): $$$x_ {11}, x_ {12}, x_ {13} ... x_ {1n}$ , for the 2nd regressor (for example, the Fed rate): $$$x_ {21}, x_ {22}, x_ {23} ... x_ {2n}$ for $$$k$ th "regressor: $$$x_ {k1}, x_ {k2}, x_ {k3} ... x_ {kn}$

Dependence of targets on regressors

Assume Target Dependence $$$y_i$ from regressors " $$$i$ -th "observation can be expressed through the linear regression equation of the form:

$$

$$f (w, x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

where $$$x_i$ - " $$$i$ th "regressor value from 1 to $$$n$ ,

$$$k$ - the number of regressors from 1 to $$$k$

$$$w$ - angular coefficients that represent the amount by which the calculated target indicator will change on average when the regressor changes.

In other words, we are for everyone (except $$$w_0$ ) of the regressor we determine “our” coefficient $$$w$ , then multiply the coefficients by the values ​​of the regressors " $$$i$ -th "observation, as a result we get a certain approximation" $$$i$ th "target.

Therefore, we need to select such coefficients $$$w$ for which the values ​​of our approximating function $$$f (w, x_i)$ will be located as close as possible to the values ​​of the targets.

Estimation of the quality of the approximating function

We will determine the quality estimate of the approximating function by the least squares method. The quality assessment function in this case will take the following form:

$$

$$Err = \ sum \ limits_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

We need to choose such values ​​of the coefficients $ w $ for which the value $$$Err$ will be the smallest.

We translate the equation into matrix form

Vector view

First, to make your life easier, you should pay attention to the linear regression equation and note that the first coefficient $$$w_0$ not multiplied by any regressor. Moreover, when we translate the data into matrix form, the above circumstance will seriously complicate the calculations. In this regard, it is proposed to introduce another regressor for the first coefficient $$$w_0$ and equate to one. Or rather, each " $$$i$ the "value" of this regressor to equate to unity - because when multiplied by unity, nothing will change in terms of the result of calculations, and from the point of view of the rules for the product of matrices, our torment will be significantly reduced.

Now, for a while, to simplify the material, suppose we have only one " $$$i$ th "observation. Then, imagine the values ​​of the regressors" $$$i$ th observation as a vector $$$\ vec {x_i}$ . Vector $$$\ vec {x_i}$ has dimension $$$(k \ times 1)$ , i.e $$$k$ rows and 1 column:

$$

$$\ vec {x_i} = \ begin {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

The desired coefficients can be represented as a vector $$$\ vec {w}$ having dimension $$$(k \ times 1)$ :

$$

$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

The linear regression equation for " $$$i$ -th "observation will take the form:

$$

$$f (w, x_i) = \ vec {x_i} ^ T \ vec {w}$$

The quality assessment function of the linear model will take the form:

$$

$$Err = \ sum \ limits_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

Note that in accordance with the rules of matrix multiplication, we needed to transpose the vector $$$\ vec {x_i}$ .

Matrix representation

As a result of the multiplication of vectors, we get the number: $$$(1 \ times k) \ centerdot (k \ times 1) = 1 \ times 1$ as expected. This number is the approximation " $$$i$ -th "target. But we need to approximate not one value of the target, but all. To do this, we write everything" $$$i$ matrix regressors $$$X$ . The resulting matrix has the dimension $$$(n \ times k)$ :

$$$$ display $$ X = \ begin {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $$ display $$

Now the linear regression equation will take the form:

$$

$$f (w, X) = X \ vec {w}$$

Denote the values ​​of the target indicators (all $$$y_i$ ) per vector $$$\ vec {y}$ dimension $$$(n \ times 1)$ :

$$

$$\ vec {y} = \ begin {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

Now we can write in the matrix format the equation for assessing the quality of a linear model:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

Actually, from this formula we further obtain the formula known to us $$$X ^ T X w = X ^ T y$

How it's done? The brackets are opened, differentiation is carried out, the resulting expressions are transformed, etc., and that is what we are going to do now.

Matrix transformations

Expand the brackets

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

Prepare an equation for differentiation

To do this, we carry out some transformations. In subsequent calculations, it will be more convenient for us if the vector $$$\ vec {w} ^ T$ will be presented at the beginning of each work in the equation.

Conversion 1

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

How did it happen? To answer this question, just look at the sizes of the multiplied matrices and see that at the output we get a number or otherwise $$$const$ .

We write the dimensions of the matrix expressions.

$$$\ vec {y} ^ TX \ vec {w}: (1 \ times n) \ centerdot (n \ times k) \ centerdot (k \ times 1) = (1 \ times 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ times k) \ centerdot (k \ times 1)) ^ T \ centerdot (n \ times 1) = (1 \ times n) \ centerdot (n \ times 1) = (1 \ times 1) = const$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ times k) \ centerdot (k \ times n) \ centerdot (n \ times 1) = (1 \ times 1) = const$

Conversion 2

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

We write similarly to transformation 1

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ times k) \ centerdot (k \ times 1)) ^ T \ centerdot (n \ times k) \ centerdot (k \ times 1 ) = (1 \ times 1) = const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ times k) \ centerdot (k \ times n) \ centerdot (n \ times k) \ centerdot (k \ times 1) = (1 \ times 1) = const$

At the output, we get an equation that we have to differentiate:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

We differentiate the function of assessing the quality of the model

Differentiate by vector $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) '- (2 \ vec {w} ^ TX ^ T \ vec {y})' + (\ vec {y} ^ T \ vec {y }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

Questions why $$$(\ vec {y} ^ T \ vec {y}) '= 0$ should not be, but the operations to determine the derivatives in the other two expressions, we will analyze in more detail.

Differentiation 1

We reveal the differentiation: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

In order to determine the derivative of a matrix or vector, you need to see what they have inside. We look:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $$$ $ inline $ X = \ begin {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

Denote the product of matrices $$$X ^ TX$ through the matrix $$$A$ . Matrix $$$A$ square and moreover, it is symmetrical. These properties will be useful to us further, remember them. Matrix $$$A$ has dimension $$$(k \ times k)$ :

$$$ inline $ A = \ begin {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ inline $

Now our task is to correctly multiply the vectors by the matrix and not get “twice two five”, so we will focus and be extremely careful.

$$$ inline $ \ vec {w} ^ TA \ vec {w} = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ times \ begin {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \ \ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$ inline $ = \ begin {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$= \ begin {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_0a_ {0k} w_k + w_1a_ {1k} w_k + .. . + w_k ^ 2a_ {kk}$

However, we got an intricate expression! In fact, we got a number - a scalar. And now, already truly, we pass to differentiation. It is necessary to find the derivative of the obtained expression for each coefficient $$$w_0 w_1 ... w_k$ and get the dimension vector at the output $$$(k \ times 1)$ . Just in case, I will describe the procedures for the actions:

1) differentiate by $$$w_o$ we get: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) differentiate by $$$w_1$ we get: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) differentiate by $$$w_k$ we get: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

At the output, the promised vector of size $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

If you take a closer look at the vector, you will notice that the left and corresponding right elements of the vector can be grouped in such a way that, as a result, the vector can be distinguished from the presented vector $$$\ vec {w}$ the size $$$(k \ times 1)$ . For instance, $$$w_1a_ {10}$ (left element of the top line of the vector) $$$+ a_ {01} w_1$ (the right element of the top line of the vector) can be represented as $$$w_1 (a_ {10} + a_ {01})$ , a $$$w_2a_ {20} + a_ {02} w_2$ - as $$$w_2 (a_ {20} + a_ {02})$ etc. on each line. Group:

$$

$$\ begin {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ { 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ {k1} + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_ {2k } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

Take out the vector $$$\ vec {w}$ and at the output we get:

$$$$ display $$ \ begin {pmatrix} 2a_ {00} & a_ {10} + a_ {01} & a_ {20} + a_ {02} & ... & a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10} & 2a_ {11} & a_ {21} + a_ {12} & ... & a_ {k1} + a_ {1k} \\ ... & ... & .. . & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & .. . \\ a_ {0k} + a_ {k0} & a_ {1k} + a_ {k1} & a_ {2k} + a_ {k2} & ... & 2a_ {kk} \ end {pmatrix} \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ display $$

Now, let's take a look at the resulting matrix. A matrix is ​​the sum of two matrices $$$A + A ^ T$ :

$$$$ display $$ \ begin {pmatrix} a_ {00} & a_ {01} & a_ {02} & ... & a_ {0k} \\ a_ {10} & a_ {11} & a_ {12} & ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & a_ {k2} & ... & a_ {kk} \ end {pmatrix} + \ begin {pmatrix} a_ {00} & a_ {10} & a_ {20} & ... & a_ {k0} \\ a_ {01} & a_ {11} & a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} & a_ {1k} & a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $$ display $$

Recall that a little earlier, we noted one important property of the matrix $$$A$ - it is symmetrical. Based on this property, we can confidently state that the expression $$$A + A ^ T$ equals $$$2A$ . This is easy to verify by revealing the matrix-by-element product $$$X ^ TX$ . We will not do this here, those who wish can conduct a check on their own.

Let's get back to our expression. After our transformations, it turned out as we wanted to see it:

$$

$$(A + A ^ T) \ times \ begin {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

So, we coped with the first differentiation. We pass to the second expression.

Differentiation 2

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

Let's go along the beaten path. It will be much shorter than the previous one, so do not go far from the screen.

We reveal the element-wise vectors and matrix:

$$$ inline $ \ vec {w} ^ T = \ begin {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$ inline $ X ^ T = \ begin {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

$$$\ vec {y} = \ begin {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

For a while, we remove the deuce from the calculations - it does not play a big role, then we will return it to its place. Multiply the vectors by the matrix. First of all, we multiply the matrix $$$X ^ T$ on vector $$$\ vec {y}$ , here we have no restrictions. Get the size vector $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Perform the following action - multiply the vector $$$\ vec {w}$ to the resulting vector. At the output, a number will wait for us:

$$

$$\ begin {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

We then differentiate it. At the output we get a dimension vector $$$(k \ times 1)$ :

$$

$$\ begin {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

Does it resemble something? All right! This is the product of the matrix. $$$X ^ T$ on vector $$$\ vec {y}$ .

Thus, the second differentiation was successfully completed.

Instead of a conclusion

Now we know how equality came about. $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ .

Finally, we describe a quick way to transform the main formulas.

Estimate the quality of the model in accordance with the least squares method:
$$$\ sum \ limits_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limits_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20mu = \ mkern 20mu (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

We differentiate the resulting expression:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ Previous work of the author - “We solve the equation of simple linear regression”
$$$\ rightarrow$ The next work of the author - "Chewing Logistic Regression"

Literature

Internet sources:

1) habr.com/en/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/en/post/307004
4) nabatchikov.com/blog/view/matrix_der

Textbooks, task collections:

1) Lecture notes on higher mathematics: full course / D.T. Written - 4th ed. - M.: Iris Press, 2006
2) Applied Regression Analysis / N. Draper, G. Smith - 2nd ed. - M.: Finance and Statistics, 1986 (translated from English)
3) Tasks for solving matrix equations:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html