Este es el segundo artículo del equipo de configuración sobre nuestra experiencia en la creación de robots autónomos para las competiciones Eurobot Open y el uso de ROS para esto.
El primer artículo trata sobre la mecánica y la arquitectura general de los robots.Los robots viajan en un campo plano y la mayoría de los obstáculos se conocen de antemano, sin embargo, los oponentes insidiosos pueden intentar robar nuestros recursos (y a veces queremos comer un par de docenas de puntos extra), mientras que queremos conducir al punto deseado lo más rápido posible y no tocar los obstáculos. De una cámara externa en el campo, obtenemos datos sobre la posición del enemigo y sabemos dónde está ahora. Sin embargo, no es suficiente conocer su posición: debe poder utilizar esta información.
Hoy intentaremos conducir desde el punto A al punto B sin haber recorrido la cola de un gato que se ha quedado dormido en el campo. En particular, explicaremos cómo construimos una ruta y controlamos la velocidad del robot, y explicaremos cómo iniciar todo en nuestra computadora.
Tratando de salir con un poco de sangre
Al resolver este problema, puede llevar material preparado por escrito por profesionales, entonces no habrá tormento e invención de la próxima "bicicleta". Usamos una plataforma con ruedas omnidireccionales, por lo que, aunque hubo un intento de utilizar una cepilladora local ya preparada de ROS, por varias razones, encontraron que esto no era prometedor. A continuación puede ver la cantidad de material que necesita el diseñador de un planeador estándar:
class TrajectoryPlanner{ friend class TrajectoryPlannerTest;
Este es un ejemplo de inicialización de parámetros para regular velocidades y la trayectoria como un todo.Parámetros importantes para un cálculo completo:
- Parámetro world_model.
- Parámetro de mapa de costos: un enlace a un mapa que contiene obstáculos, así como su "extensión virtual", teniendo en cuenta la posible colisión.
De las ventajas de la pila estándar, puede resaltar la disponibilidad de documentación y la capacidad de encontrar información en los foros.
Puedes leer más en el sitio web oficial con documentaciónEs importante mencionar que los paquetes ROS se escribieron para plataformas de dos ruedas y bajo Omni se optimizaron al aumentar el ángulo de rotación disponible cuando se mueve hasta 360 grados, lo que sin duda es una muleta.
Después de analizar el proyecto, nos dimos cuenta de que habría dificultades para estudiar y complementar, así como también hay muchos chips pesados que no necesitamos. Parece, déjelos ser, pero usamos Odroid xu4 (el procesador del cual todavía estaba en Samsung s5), y los resultados de rendimiento fueron deprimentes, y el espacio para algo más potente (y la frambuesa 4 y el procesador jetson nano fuman nerviosamente en comparación con con él) no. Tuve que abandonar la pila estándar e intentar crear nosotros mismos el planificador global, el planificador local y el regulador de trayectoria
Planificador global, planificador local, regulador de trayectoria y todo todo
Se necesitan planeadores globales y locales para obtener indicaciones para llegar al destino. ¿Por qué es necesaria la separación? ¿Por qué no puedes tomar
A * y montarlo? Como regla general, el planificador global, al construir una ruta, puede usar el mapa completo en su trabajo, por lo que el algoritmo debe ser lo más rápido posible, quizás incluso con algunas simplificaciones. Para suavizar estas simplificaciones, también utilizan el planificador local, que, basándose en el resultado del planificador global (o simplemente en un área limitada alrededor del robot), trata de tener en cuenta todos los matices.
Después de construir la ruta, sabemos a dónde debe ir el robot, pero ¿cómo se le puede informar al respecto? Para hacer esto, hay un regulador de trayectoria. Calcula a qué velocidad y en qué dirección debe moverse el robot en ese momento para no desviarse de la trayectoria. En muchos sentidos, este paquete es responsable de lo rápido y hermoso que irá el robot.
Además de estas tres entidades, hay un cuarto, un servidor de mapas, que le permite procesar convenientemente el estado del mundo. Establece cómo describimos el mapa, qué posibilidades tenemos cuando trabajamos con el mapa y, de muchas maneras, determinamos la velocidad de los planeadores.
Antes de continuar con la descripción de la pila de navegación, sería bueno describir las razones por las que se eligió cost_map como servidor de mapas. En general, probamos diferentes opciones para el controlador de mapas:
Occupancy_grid ,
Grid_map ,
Cost_map , pero
decidimos por el último.
Razones:
- Convenientemente interactuar con el mapa.
- Hay varios iteradores que necesitamos en varias formas (circular, lineal, rectangular, etc.).
- Puede almacenar múltiples capas de mapa con diferentes parámetros.
- Buena gestión de la memoria.
- Y lo más importante, la velocidad. El mapa de cuadrícula funciona con doble tipo y, debido a esto, es varias veces más lento que los servidores de mapas que usan int8 para trabajar.
A pesar de que la cuadrícula de ocupación también funciona con int8, no puede presumir de la misma usabilidad, por lo que tuve que abandonarla.
Desde el mapa, necesitamos saber dónde están las zonas libres, peligrosas e irresistibles. Para cada objeto que está en el campo, podemos ajustar el campo de inflación, un valor que, dependiendo de la distancia al objeto, caracteriza la permeabilidad de la celda. La inflación es la cola del gato, es fácil no notarlo, pero luego te arrepentirás durante mucho tiempo. Mapeamos robots enemigos y agregamos una zona de peligro que solo el planificador local tiene en cuenta. El planificador global ignora todos los puntos, si no son un obstáculo.
Planificador global
Lo primero que escribieron en navegación es el planificador global. Se basa en el algoritmo theta *. En resumen, esta es una
A * modificada, donde el énfasis está en encontrar el nodo padre, al que se puede llegar directamente, es decir. No hay obstáculos para ella. Esto nos permite construir caminos convenientes y suaves que se utilizan en el planificador local.
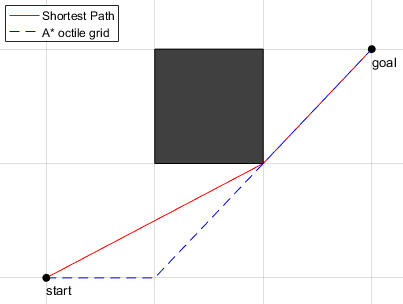Comparación de A * y theta *Para el planificador global, tenemos un archivo con parámetros (params / path_planner.yaml) que describe los temas del mapa y los temas con la ubicación de todos los robots (para los cuatro robots en el campo, donde "nulo" es el tema con datos sobre el robot actual).
# small robot debug param list robot_id: "small" ########################### # cost_map_server params ## ########################### cost_map_server/big_robot_size: 0.45 cost_map_server/little_robot_size: 0.45 cost_map_server/cube_size: 0.11 cost_map_server/inscribed_radius: 0.3 cost_map_server/inflation_radius: 0.3 cost_map_server/inflation_exponential_rate: 0.6 cost_map_server/big_robot1: "/aruco/big_robot" cost_map_server/big_robot2: "/aruco/enemy_robot1" cost_map_server/small_robot1: "null" cost_map_server/small_robot2: "/aruco/enemy_robot2" cost_map_server/collision: "collision" cost_map_server/image_resource_name: "$(find cost_map_server)/param/image_resource.yaml" cost_map_server/min_diff_points: 0.01 ########################### ### path_planner params ### ########################### global_planner/path_layer: "inflation_layer" global_planner/path_force_layer: "obstacle_inflation_layer" global_planner/frame_id: "map" global_planner/current_position: "real_corr" global_planner/path_filter_epsilon: 0
También indica:
- uno de los algoritmos que puedes elegir para construir una ruta,
- nombres de capas en las que construiremos la ruta en sí,
- un tema sobre nuestra posición, donde se emiten los datos filtrados (en nuestro caso es una combinación de datos de ubicación de la cámara y la odometría).
El algoritmo de búsqueda de ruta en sí mismo, Theta Star, se resalta en un archivo separado (src / global_planner.cpp) para la conveniencia de agregar nuevos algoritmos:
float cost_so_far[300][200]; PriorityPoint neighbors[8]; PriorityPoint current; int come_from[300][200][2]; double makePath_ThetaStar(std::vector<cost_map::Index> &path, PriorityPoint start, PriorityPoint goal, std::string layer, cost_map::CostMap &cost_map, double grid_cost, bool only_cost) { std::priority_queue<PriorityPoint, std::vector<PriorityPoint>, myCompare> openSet; size_t max_x = cost_map.getSize()[0]; size_t max_y = cost_map.getSize()[1]; std::fill_n(*cost_so_far, max_x * max_y, std::numeric_limits<float>::max()); cost_so_far[start.x][start.y] = 0; come_from[start.x][start.y][0] = start.x; come_from[start.x][start.y][1] = start.y; openSet.push(start); grid_cost=5; while (!openSet.empty()) { current = openSet.top(); openSet.pop(); if (current == goal) { break; } current.GetNeighbors(neighbors); float current_cost = cost_so_far[current.x][current.y]; int parent_carent[2] ={come_from[current.x][current.y][0], come_from[current.x][current.y][1]}; for (int i = 0; i < 8; i++) { if (!neighbors[i].OnMap(max_x, max_y)) { continue; } bool onLine = lineOfSight(parent_carent[0], parent_carent[1], neighbors[i].x, neighbors[i].y, cost_map, layer, grid_cost + 1); if (onLine) { float new_cost = cost_so_far[parent_carent[0]][parent_carent[1]] + HeuristicEvclid(parent_carent, neighbors[i], grid_cost*10); if (new_cost < cost_so_far[neighbors[i].x][neighbors[i].y]) { cost_so_far[neighbors[i].x][neighbors[i].y] = new_cost; neighbors[i].priority = HeuristicEvclid(neighbors[i], goal, grid_cost*10) + new_cost; openSet.push(neighbors[i]); come_from[neighbors[i].x][neighbors[i].y][0] = parent_carent[0]; come_from[neighbors[i].x][neighbors[i].y][1] = parent_carent[1]; } } else { float neighbor_price = cost_map.at(layer, cost_map::Index({neighbors[i].x, neighbors[i].y})) + neighbors[i].priority; float new_cost = current_cost + neighbor_price; if (new_cost < cost_so_far[neighbors[i].x][neighbors[i].y]) { cost_so_far[neighbors[i].x][neighbors[i].y] = new_cost; neighbors[i].priority =HeuristicEvclid(neighbors[i], goal, grid_cost*10) + new_cost; openSet.push(neighbors[i]); come_from[neighbors[i].x][neighbors[i].y][0] = current.x; come_from[neighbors[i].x][neighbors[i].y][1] = current.y; } } } } if (only_cost) { return cost_so_far[current.x][current.y]; } path.clear(); PriorityPoint temp_point; while (current != start) { path.push_back({current.x, current.y}); temp_point.x = come_from[current.x][current.y][0]; temp_point.y = come_from[current.x][current.y][1]; current = temp_point; } path.push_back({current.x, current.y}); return 0; }
Un algoritmo para eliminar puntos adicionales en la ruta RamerDouglasPeucker también se asigna a un archivo separado.
Elimina puntos del camino si está más allá de una distancia dada de la línea que conecta dos puntos vecinos.
Planificador local
Él trabaja para nosotros sobre la base del descenso de gradiente en un campo potencial. Como entrada, el camino desde el planificador global. Sin embargo, esto no es todo de lo que es capaz. En local_planner, hay servicios internos para elegir el modo de construcción de ruta. Hay dos modos de funcionamiento en total: el modo de desplazamiento de puntos a lo largo del gradiente, utilizando múltiples pases en el mapa, así como el modo de desplazamiento, en el que calculamos inmediatamente el incremento en dos coordenadas y movemos el punto al borde de la zona segura. Si el punto cae en varias de esas zonas, entonces cambiamos a los lugares de su intersección, porque allí es más seguro.
El modo de operación es el siguiente: si no hay ningún obstáculo en el camino desde la iteración anterior, entonces rompemos el camino cada 2 cm y luego lo desplazamos a lo largo del gradiente; de lo contrario, usamos el segundo modo de operación del planificador local.
La segunda opción es bastante ligera y, como el planificador global, no carga mucho el procesador. Utilizamos varias versiones de este algoritmo y varias manipulaciones con el mapa. Por ejemplo, intentamos escribir un gráfico en el que los vértices se encuentran cada 10 cm y se desplazan por un máximo de 4 cm, después de lo cual se utilizó el algoritmo de Dijkstra en el gráfico obtenido para encontrar la distancia más pequeña. El punto final en este caso usa el punto de desplazamiento más cercano. Pero dicho algoritmo era más adecuado para el planificador global y decidimos abandonar esta implementación.
También intentamos usar la construcción de caminos desde cero usando el método de descenso de gradiente. Este método fue el primero que decidimos escribir. Resultó no ser eficiente en memoria (ocupaba más de 400 mb de RAM pura, ya que usaba un mapa de costos con cada pasada) y lento. El control de frecuencia se apagó debido a una optimización deficiente y la velocidad era inferior a 30 veces por segundo, lo que no nos convenía.
Como resultado, decidimos usar el descenso de gradiente en un campo potencial basado en el camino del planeador global. Resultó ser un algoritmo liviano y relativamente simple, que nos conviene completamente en términos de calidad de ruta, tiempo de trabajo y la cantidad de RAM utilizada en la región de 100-150 mb, que es varias veces menor que en las primeras iteraciones de desarrollo.
Un ejemplo de una ruta desplazada por un cepillo localA diferencia de global_planner, los parámetros en local_planner son extremadamente pequeños, lo que se debe a su simplicidad, porque todas las tareas más importantes recaen en global_planner:
grid_map_server/big_robot1 : 0.4 grid_map_server/big_robot2 : 0.4 grid_map_server/small_robot1 : 0.4 grid_map_server/small_robot2 : 0.4 local_planner/radius : 0.15 global_planner/frame_id : "map"
En este caso, configuramos:
- Radios de zonas seguras para cada uno de los robots.
- Recorrido máximo de desplazamiento por cepillo local.
- El nombre de la capa de mapa con la que estamos trabajando.
En una clase separada se asignaron todas las funciones más importantes. En este caso, es un desglose recursivo del camino, la creación de un planeador y constructores y destructores virtuales.
class Planner { public: Planner(double inflation_radius_, std::string frame_id_) { inflation_radius = inflation_radius_; for (int i = 0; i < 300; i++) { for(int j = 0; j < 200; j++) our_map[i][j] = 3000.0; } OurPath->poses.resize(50); geometry_msgs::Pose pose; pose.position.x = 0.0; pose.position.y = 0.0; for( int i = 0; i < 50; i++) { OurPath->poses[i].pose = pose; } frame_id = frame_id_; } virtual ~Planner() { } virtual void UpdatePath() = 0; ros::Publisher move_pub; ros::Publisher BigEnemyPub; ros::Publisher LittleEnemyPub; ros::Publisher local_path_publisher; protected:
La clase LocalPlanning se heredó de ella, donde se encuentra todo el núcleo del planeador, es decir, desplazando puntos al borde de la zona segura y decidiendo qué hacer específicamente con la ruta.
Todas las demás funciones se resaltan en un archivo separado fichi.hpp, y el descenso de gradiente en potencial_campo.hpp. A continuación se muestra una instantánea de este archivo, que muestra las funciones para crear un campo potencial en el mapa cost_map:
double CalcAttractivePotential(grid_map::Index index, double goalx, double goaly) { return sqrt(pow(index[0] - goalx, 2) + pow(index[1] - goaly, 2)); } void CalcPotential(double startx, double starty, double goalx, double goaly, cost_map::CostMap &cost_map, double (&our_map)[300][200]) {
Regulador de trayectoria
Por último, pero no menos importante, es el regulador de trayectoria. Es responsable de convertir la ruta del planificador local en una ruta y proporciona la velocidad para el paso actual.
Su primera versión, que utilizamos en la final de Eurobot 2018, es una mezcla del controlador pid de aceleración y frenado, donde el vector se normaliza al siguiente punto en el camino, en relación con la distancia al punto final.
En resumen, el controlador PID es la suma de los tres estados del sistema que ayudan a corregir el sistema y los errores aleatorios que a veces ocurren.
Estas funciones se seleccionaron empíricamente y dependen de la distancia al punto final de la ruta (puede ser cuadrática, cúbica, inversa, pero luego nos decidimos por la cuadrática). Esto funcionó, pero lo único que no nos convenía era que el robot no podía frenar a tiempo a velocidades superiores a 0,7 metros por segundo. Por lo tanto, cuando llegó el momento, decidimos reconstruir todo el algoritmo.
La primera iteración en el camino hacia la nueva trayectoria fue el reemplazo del vector al que íbamos. Ahora era la suma de los vectores para los próximos tres con diferentes coeficientes. La segunda iteración fue la escritura mínima jerk. En resumen, esta es una construcción de un polinomio de quinto grado, donde las coordenadas x e y dependen del tiempo de llegada a cada punto.
La figura muestra un gráfico de una de las coordenadas en función del tiempo, así como la velocidad a lo largo de esta coordenada.Este tipo de regulador de trayectoria nos convenía más, ya que requería menos manipulación con la selección de diferentes coeficientes, porque todos los coeficientes son los valores en el polinomio, que se calcularon en función del tiempo de llegada, la velocidad y aceleración actuales, la velocidad de salida y la aceleración.
El resultado de la reescritura de la trayectoria fue que logramos duplicar la velocidad promedio del robot.
Como en los dos casos anteriores, todas las funciones principales se asignan en un archivo separado para facilitar la interacción. Esta vez, la clase PlannerTrajectory es responsable de construir una trayectoria basada en MinimumJerk
typedef struct State { double velocity; double acceleration; State(double v_, double a_) : velocity(v_), acceleration(a_) {} State() { velocity = 0; acceleration = 0; } }; class PlannerTrajectory { private: nav_msgs::Path global_path; cost_map::CostMap *costmap_ptr; geometry_msgs::PoseStamped Goal_pred; std::vector<double> trajectory_x; std::vector<double> trajectory_y; double average_velocity = 80;
La foto muestra todas las variables declaradas que utilizamos.Todo lo demás se resalta en otro archivo (include / trajectory_regulator.h): recibir puntos de temas, decidir si pasar al siguiente punto (si está en un obstáculo, entonces no vamos) y mucho más.
Migrando a ROS Melodic
Hasta el año pasado, utilizamos el lanzamiento lte de ROS - ROS Kinetic. Generalmente nos conviene, pero su apoyo está llegando a su fin el próximo año, y muchos de los paquetes que necesitamos comenzaron a salir exclusivamente para ROS Melodic. Y luego resultó que el costmap_server que utilizamos no está bajo Melodic.
Hubo un problema al procesar los datos de las tarjetas.
Elegimos el mapa de cuadrícula, ya que la pila es similar, pero el comienzo del mapa está en un lugar diferente, y los valores del mapa en sí varían de 0 a 1. Esto se ha convertido en un gran problema en toda la pila de navegación. Si antes el planificador global se lanzaba 50 veces por segundo (había restricciones de frecuencia y, por lo tanto, el procesador no se usaba demasiado, incluso en la mitad de un hilo), ahora allanó el camino cada dos segundos y lo consideró malo: cargó completamente un núcleo. En 2 segundos, el robot podría cruzar todo el mapa. Esto no nos convenía, y los intentos de paralelizar este proceso terminaron en un fracaso, porque entonces no quedaba rendimiento para otros proyectos (teniendo en cuenta los costos de la paralelización).
Decidimos cambiar la pila nuevamente, abandonar el mapa de cuadrícula a favor de la cuadrícula de ocupación. Ha aparecido un nuevo problema: la incapacidad de almacenar varias versiones de mapas al mismo tiempo (por ejemplo, un mapa completo con todos los obstáculos y un mapa estático con solo obstáculos dinámicos). Tendría que cambiar la mitad del código, que no era particularmente confiable. Por lo tanto, decidimos buscar soluciones alternativas a este problema.
Servidor de mapas de costos
Después de una larga búsqueda, encontramos mapas de horquillas costmap_serverr:
https://github.com/lelongg/cost_map.git , extremadamente útiles para nuestro sistema de horquillas.
Y ahora, en lugar de dar servicio solo al mapa de cuadrícula, para la entrega, logramos calcular la ubicación probable del enemigo en función de la predicción del filtro de Kalman.
Una de las cosas más importantes para un servidor de mapas es un archivo de mapa, que se utiliza para la creación inicial de todas las capas, que posteriormente solo se actualizan. Es una imagen binaria png, donde el negro es un obstáculo y el blanco es una zona libre.
También hay un archivo de configuración para la configuración cost_map_server. Contiene temas con puntos enemigos, una zona de inflación y el tamaño del cuadrado, que también se pueden usar para poner la zona peligrosa del enemigo en el mapa.
########################### # cost_map_server params ## ########################### cost_map_server/big_robot_size: 0.4 cost_map_server/little_robot_size: 0.4 cost_map_server/cube_size: 0.11 cost_map_server/inscribed_radius: 0.25 cost_map_server/inflation_radius: 0.25 cost_map_server/inflation_exponential_rate: 0.6 cost_map_server/big_robot1: "/aruco/robot1" cost_map_server/big_robot2: "/aruco/robot2" cost_map_server/small_robot1: "/aruco/robot3" cost_map_server/small_robot2: "/aruco/robot4" cost_map_server/collision: "collision" cost_map_server/image_resource_name: "$(find cost_map_server)/param/image_resource.yaml" cost_map_server/min_diff_points: 0.01
Todas las capas se publican solo si alguien se suscribe a ellas:
void PublishChanges() { nav_msgs::OccupancyGrid msg; cost_map_msgs::CostMap cost_map_msg; if (obstacle_inflation_publisher.getNumSubscribers() > 0) { cost_map::toOccupancyGrid(costmap, "obstacle_layer", msg); obstacle_inflation_publisher.publish(msg); } if (inflation_publisher.getNumSubscribers() > 0) { cost_map::toOccupancyGrid(costmap, "inflation_layer", msg); inflation_publisher.publish(msg); } if (cost_map_publisher.getNumSubscribers() > 0) { cost_map::toMessage(costmap, cost_map_msg); cost_map_publisher.publish(cost_map_msg); } }
Ejecutar en su computadora
Para comenzar la pila completa, debe:
- Poner ROS
- roslaunch cost_map_server cost_map_server_alone.launch - para iniciar el mapa
- roslaunch global_planner global_planner.launch: inicia el planeador global con parámetros
- rosparam load $ (find local_planner) /param/param.yaml
- rosrun local_planner local_planning
- rosrun trayectoria_regulador trayectoria_regulador
- rosrun global_planner mover
- rosrun rviz
- agregar capa_inflacion
- Ahora enviando un mensaje al tema / gp / objetivo enviamos el robot al punto deseado
Como resultado del lanzamiento de todos los elementos, tendrá una simulación lista para iniciar nuestra pila en su computadora. Horquilla necesariaInicialmente, necesitábamos una navegación que ayudara a nuestro robot a conducir de manera hermosa, rápida y precisa sobre ruedas omnidireccionales. Durante la preparación para la competencia, ni un solo gato resultó herido, y el robot es guapo. Como resultado, tenemos una pila de navegación ligera para concursos similares a eurobot, con lo que estamos bastante satisfechos.Para nosotros, esta pila es mejor que la estándar, pero ...Nuestro Telegrama: t.me/SetUpSberEl repositorio de toda nuestra creatividad