Al extraer información, a menudo surge la tarea de encontrar dichos fragmentos de texto. En el contexto de una búsqueda, el usuario puede generar una consulta (por ejemplo, el texto que el usuario ingresa en el motor de búsqueda) o el propio sistema. A menudo necesitamos hacer coincidir una consulta entrante con consultas ya indexadas. En este artículo, veremos cómo puede construir un sistema que resuelva este problema en relación con miles de millones de solicitudes sin gastar una fortuna en la infraestructura del servidor.

Primero, definimos formalmente el problema:

Dado un conjunto fijo de consultas $$$Q$ solicitud entrante $$$q$ y entero $$$k$ . Necesito encontrar un subconjunto de consultas $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subset Q$ a cada solicitud $$$q_ {i} \ en R$ fue más como $$$q$ que cualquier otra solicitud en $$$Q ∖ R$ .

Por ejemplo, con este conjunto de consultas $$$Q$ :

{tesla cybertruck, beginner bicycle gear, eggplant dishes, tesla new car, how expensive is cybertruck, vegetarian food, shimano 105 vs ultegra, building a carbon bike, zucchini recipes} 

y $$$k = 3$ Puede esperar este resultado:


Tenga en cuenta que todavía no hemos definido un criterio de similitud . En este contexto, esto puede significar casi cualquier cosa, pero generalmente se reduce a alguna forma de similitud basada en palabras clave o vectores. Usando la similitud basada en palabras clave, podemos encontrar dos consultas similares si contienen suficientes palabras comunes. Por ejemplo, las consultas "abrir un restaurante en munich" y "mejor restaurante de munich" son similares porque contienen las palabras "restaurante" y "munich". Y las consultas "mejor restaurante de munich" y "dónde comer en munich" ya son menos similares, porque solo tienen una palabra en común. Sin embargo, alguien que busque un restaurante en Munich estaría mejor si el segundo par de solicitudes resultara similar. Y en esto ayudaremos a la comparación basada en vectores.

Representación vectorial de palabras

La representación vectorial de palabras es una técnica de aprendizaje automático utilizada en el procesamiento del lenguaje natural para convertir texto o palabras en vectores. Moviendo la tarea al espacio vectorial, podemos usar operaciones matemáticas con vectores, sumando y calculando distancias. Para establecer enlaces entre palabras similares, puede usar métodos tradicionales de agrupación de vectores. El significado de estas operaciones en el espacio de palabras original puede no ser obvio, pero la ventaja es que ahora tenemos acceso a una amplia gama de herramientas matemáticas. Si está interesado en los detalles sobre los vectores de palabras y su aplicación, lea sobre word2vec y GloVe .

Tenemos una forma de generar vectores a partir de palabras, ahora los recopilaremos en vectores de texto (vectores de documentos o expresiones). La forma más fácil de hacer esto es agregando (o promediando) los vectores de todas las palabras en el texto.


^{Figura 1: Vectores de consulta.}

Ahora puede determinar la similitud de dos fragmentos de texto (o consultas) representándolos en el espacio vectorial y calculando la distancia entre los vectores. Típicamente, se usa una distancia angular para esto.

Como resultado, la representación vectorial de las palabras permite la coincidencia textual de un tipo diferente, lo que complementa la coincidencia basada en palabras clave. Puede explorar la similitud semántica de las solicitudes (por ejemplo, "el mejor restaurante de munich" y "dónde comer en munich"), como no podíamos hacer antes.

Búsqueda aproximada de vecinos más cercanos

Ahora podemos refinar nuestro problema original de coincidencia de consultas:

Dado un conjunto fijo de vectores de consulta $$$Q$ vector entrante $$$q$ y entero $$$k$ . Necesitas encontrar un subconjunto de vectores $$$R = \ left \ {q0, q1, ..., qk \ right \} \ subset Q$ para que la distancia angular de $$$q$ a cada vector $$$q_ {i} \ en R$ era más corta que la distancia a cualquier otro vector en $$$Q ∖ R$ .

Esto se llama la tarea de encontrar al vecino más cercano. Hay una serie de algoritmos para su solución rápida en espacios de baja dimensión. Pero cuando trabajamos con representaciones vectoriales de palabras, generalmente operamos con vectores de alta dimensión (100-1000 dimensiones). Y aquí los métodos mencionados ya no funcionan.

No hay una forma adecuada de determinar rápidamente los vecinos más cercanos en espacios de alta dimensión. Por lo tanto, simplificamos el problema al permitir el uso de resultados aproximados: en lugar de devolver siempre los vectores más cercanos, nos contentaremos con solo algunos de los vecinos más cercanos o en cierta medida cercanos. Esto se llama la búsqueda aproximada de la tarea de vecinos más cercanos y es un área de investigación activa.

Pequeño mundo jerárquico

El gráfico jerárquico de mundo pequeño navegable ( HNSW ) es uno de los algoritmos más rápidos para la búsqueda aproximada de vecinos más cercanos. El índice de búsqueda en HNSW es ​​una estructura multinivel en la que cada nivel es un gráfico de proximidad. Cada nodo del gráfico corresponde a uno de los vectores de consulta.


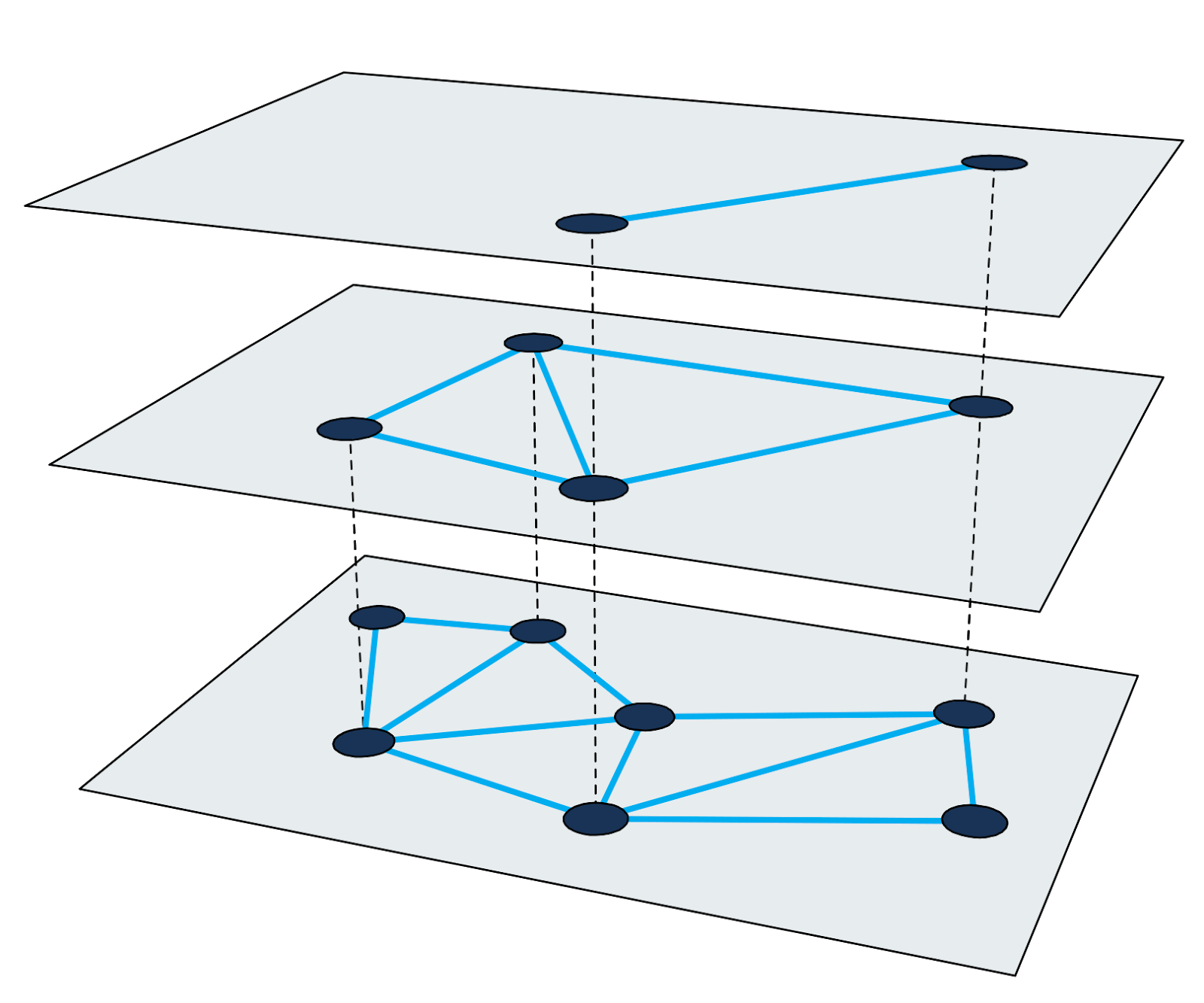^{Figura 2: Gráfico de proximidad multinivel.}
Encontrar vecinos más cercanos en HNSW utiliza el método de acercamiento. Comienza en el nodo de entrada del nivel más alto y realiza recursivamente un recorrido de gráfico codicioso en cada nivel hasta que alcanza un mínimo local en la parte inferior.

Los detalles sobre el algoritmo y la técnica de búsqueda están bien descritos en el trabajo científico. Es importante recordar que cada ciclo de búsqueda de los vecinos más cercanos consiste en atravesar los nodos de los gráficos con el cálculo de las distancias entre los vectores. Observaremos estos pasos a continuación para utilizar este método para crear un índice a gran escala.

La dificultad de indexar miles de millones de consultas

Supongamos que necesitamos indexar 4 mil millones de vectores de consulta de 200 dimensiones, con cada dimensión representada por un número de coma flotante de cuatro bytes (4 mil millones es suficiente para hacer que la tarea sea interesante, pero aún puede almacenar las ID de nodo en números regulares de cuatro bytes) . Un cálculo aproximado nos dice que el tamaño de los vectores solo será de aproximadamente 3 TB. Dado que la mayoría de las bibliotecas existentes utilizan una capacidad de RAM para una búsqueda aproximada de los vecinos más cercanos, necesitaremos un servidor muy grande para insertar al menos vectores en la RAM. Tenga en cuenta que esto no tiene en cuenta el índice de búsqueda adicional, que es necesario para la mayoría de los métodos.

En toda la historia del desarrollo de nuestro motor de búsqueda, hemos utilizado varios enfoques diferentes para resolver este problema. Consideremos algunos de ellos.

Subconjunto de datos

El primer y más simple enfoque, que no nos permitió resolver completamente el problema, fue limitar el número de vectores en el índice. Tomando una décima parte de los datos, creamos un índice que necesita, sorpresa, el 10% de la memoria. Sin embargo, la calidad de la búsqueda se ha deteriorado, porque ahora hemos operado con menos consultas.

Cuantización

Aquí utilizamos todos los datos, pero los redujimos mediante la cuantización (utilizamos diferentes técnicas de cuantificación, por ejemplo, la cuantificación del producto, pero no pudimos lograr la calidad de trabajo deseada con esta cantidad de datos). Al redondear algunos errores, pudimos reemplazar todos los números de cuatro bytes en los vectores originales con versiones cuantificadas de un solo byte. La cantidad de RAM para los vectores disminuyó en un 75%. Sin embargo, todavía necesitábamos 750 GB de memoria (sin contar el tamaño del índice en sí), y este sigue siendo un servidor muy grande.

Resolviendo problemas de memoria con Granne

Los enfoques descritos tenían sus ventajas, pero requerían muchos recursos y daban una mala calidad de búsqueda. Aunque hay bibliotecas que responden en menos de 1 ms, podríamos sacrificar la velocidad a cambio de menores requisitos de hardware.

Granne (vecinos más cercanos aproximados basados ​​en gráficos) es una biblioteca HNSW desarrollada y utilizada por Cliqz para buscar tales consultas. Tiene código fuente abierto, pero la biblioteca aún está en desarrollo activo. Se publicará una versión mejorada en crates.io en 2020. Está escrito en Rust con insertos de Python, diseñado para manejar miles de millones de vectores utilizando la competitividad. Desde el punto de vista de los vectores de consulta, es interesante que Granne tenga un modo especial que requiere mucha menos memoria en comparación con otras bibliotecas.

Representación compacta de vectores de consulta

Reducir el tamaño de los vectores de consulta nos dará muchos beneficios. Para hacer esto, regresemos y consideremos crear vectores. Como las consultas están formadas por palabras y los vectores de consulta son sumas de vectores de palabras, podemos negarnos explícitamente a almacenar los vectores de consulta y calcularlos según sea necesario.

Puede almacenar consultas en forma de conjuntos de palabras y usar la tabla de búsqueda para encontrar los vectores correspondientes. Sin embargo, evitamos la redirección almacenando cada consulta como una lista de ID enteros correspondientes a los vectores de palabras en la consulta. Por ejemplo, guarde la consulta "mejor restaurante de munich" como $$$[{i_ {best}}, {i_ {restaurant}}, {i_ {of}}, {i_ {munich}}]$ donde $$${i_ {best}}$ - esta es la ID de vector de la palabra "mejor", etc. Supongamos que tenemos menos de 16 millones de vectores de palabras (más de esto costará 1 byte por palabra), entonces puede usar 3 bytes para representar todas las ID de palabras. Es decir, en lugar de almacenar 800 bytes (o 200 bytes en el caso de vectores cuantificados), solo almacenaremos 12 bytes para esta solicitud (esto no es del todo cierto. Dado que las solicitudes consisten en un número diferente de palabras, también debemos almacenar el desplazamiento de la lista en el índice de palabras). esto requerirá 5 bytes por solicitud).

En cuanto a la palabra vectores, todos los necesitamos. Sin embargo, el número de palabras es mucho menor que el número de consultas que se pueden crear combinando estas palabras. Y eso significa que el tamaño de las palabras no es tan importante. Si almacena vectores de palabras como versiones de coma flotante de cuatro bytes en una matriz simple $$$v$ , entonces necesitamos menos de 1 GB por cada millón de palabras. Este volumen puede caber fácilmente en la RAM. Ahora el vector de consulta se ve así: $$${v _ {{i_ {best}}}} + {v _ {{i_ {restaurant}}} + {v _ {{i_ {of}}} + {v _ {{i_ {munich}}}}$ .

El tamaño final del envío de la consulta depende del número total de palabras en la consulta. Para 4 mil millones de consultas, esto es aproximadamente 80 GB (incluidos los vectores de palabras). En otras palabras, en comparación con los vectores de palabras originales, el tamaño disminuyó en un 97% y en comparación con los vectores cuantificados, en un 90%.

Y una cosa más. Para una búsqueda, necesitamos visitar aproximadamente 200-300 nodos del gráfico. Cada nodo tiene 20-30 vecinos. Por lo tanto, necesitamos calcular la distancia desde el vector de consulta de entrada a los vectores 4000-9000 en el índice. Y lo que es más, necesitamos generar vectores. ¿Cuánto tiempo lleva crear vectores de consulta sobre la marcha?

Resulta que con un procesador bastante nuevo, este problema se puede resolver en unos pocos milisegundos. Una solicitud que solía ejecutarse en 1 ms ahora se ejecuta en aproximadamente 5 ms. Pero luego redujimos la cantidad de memoria para vectores en un 90%. Con mucho gusto aceptamos tal compromiso.

Visualización en memoria de vectores e índices.

Arriba, resolvimos el problema de reducir la cantidad de memoria para los vectores. Pero después de resolver este problema, la estructura del índice se convirtió en un factor limitante. Ahora necesita reducir su tamaño.

En Granne, la estructura del gráfico se almacena de forma compacta en forma de una lista de adyacencia con un número variable de vecinos para cada nodo. Es decir, la memoria apenas se desperdicia en los metadatos. El tamaño de la estructura del índice depende en gran medida de los parámetros de diseño y las propiedades del gráfico. Sin embargo, para tener una idea del tamaño del índice, es suficiente decir que podemos construir un índice para 4 mil millones de vectores con un tamaño total de aproximadamente 240 GB. Esto puede ser aceptable para uso en memoria en un servidor grande, pero se puede hacer mejor.


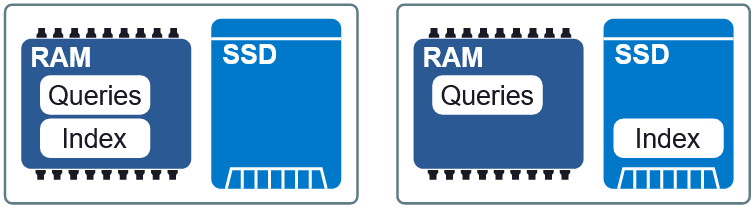^{Figura 3: Dos diseños diferentes en RAM y SSD.}

Una propiedad importante de Granne es la capacidad de mostrar el índice y los vectores de consulta en la memoria . Esto nos permite cargar perezosamente el índice y compartir memoria con múltiples procesos. Los archivos de índice y consulta se dividen en archivos de visualización separados en la memoria y se pueden usar en diferentes diseños en RAM y SSD. Si los requisitos para la demora son un poco menores, entonces colocando el índice en el SSD, las solicitudes a la RAM, mantenemos una velocidad aceptable sin un consumo excesivo de memoria. Al final del artículo veremos cómo se ve este compromiso.

Mejorando la localidad de datos

En nuestra configuración actual, cuando el índice está en un SSD, cada solicitud requiere hasta 200-300 lecturas del disco. Puede intentar aumentar la localidad de los datos organizando los elementos cuyos vectores están tan cerca que sus nodos HNSW se encuentran en el índice, no muy lejos el uno del otro. La localidad de los datos mejora el rendimiento, porque es más probable que una sola operación de lectura (generalmente extraída de 4 KB) contenga otros nodos necesarios para atravesar el gráfico. Y esto, a su vez, reduce el número de recuperaciones de datos por una búsqueda.


^{Figura 4: La localidad de datos reduce la recuperación de información.}

Cabe señalar que reordenar elementos no afecta los resultados de búsqueda, esta es una forma de acelerarlo. Es decir, el orden puede ser cualquiera, pero no todas las opciones acelerarán la búsqueda. Es muy difícil encontrar el orden óptimo. Sin embargo, la heurística que hemos utilizado con éxito es ordenar las consultas por la palabra más importante en cada consulta.

Conclusión

Utilizamos Granne para crear y mantener índices multimillonarios con vectores de consulta para buscar consultas similares con un consumo de memoria relativamente bajo. La siguiente tabla muestra los requisitos para diferentes métodos. Sea escéptico sobre los valores absolutos de los retrasos durante la búsqueda, ya que dependen en gran medida de lo que se considera una respuesta aceptable. Sin embargo, esta información describe el rendimiento relativo de los métodos.


* La asignación de un índice de memoria mayor que la cantidad requerida condujo al almacenamiento en caché de algunos nodos (visitados con frecuencia), lo que redujo el retraso en la búsqueda. No se usó caché interno para esto, solo herramientas internas del sistema operativo (kernel de Linux).

Cabe señalar que algunas de las optimizaciones mencionadas en el artículo no son aplicables para resolver el problema general de encontrar vecinos más cercanos con vectores descomponibles. Sin embargo, son aplicables en cualquier situación en la que los elementos pueden generarse a partir de menos partes (como es el caso de las palabras y las consultas). De lo contrario, aún puede usar Granne con los vectores de origen, solo requiere más memoria, como con otras bibliotecas.