Matemáticas genéricas inseguras en C #

Desafortunadamente, no fue fácil traducir adecuadamente el nombre de la fealdad que comencé al ruso. Me sorprendió descubrir que la documentación oficial de MSDN llama "plantillas" genéricas "(similar a las plantillas C++ , supongo). En la cuarta edición de "CLR vía C# " que me llamó la atención , Jeffrey Richter , traducido por Peter , los genéricos se denominan "generalizaciones", lo que refleja el concepto mucho mejor. Este artículo hablará sobre operaciones matemáticas generalizadas inseguras en C# . Teniendo en cuenta que C# no C# destinado a la informática de alto rendimiento (aunque, por supuesto, es capaz de hacerlo, pero no puede competir con el mismo C/C++ ), las operaciones matemáticas en BCL no reciben mucha atención. Intentemos simplificar el trabajo con tipos aritméticos básicos usando C# y CLR .

Declaración del problema.

Descargo de responsabilidad : el artículo contendrá muchos fragmentos de código, algunos de los cuales ilustraré con enlaces al maravilloso recurso SharpLab ( Gi r tHub ) de Andrey Shchekin .

La mayoría de los cálculos de una forma u otra se reducen a operaciones básicas. La suma, la resta (inversión, negación), la multiplicación y la división pueden complementarse con operaciones de comparación y verificación de igualdad. Por supuesto, todas estas acciones se pueden realizar fácil y simplemente en variables de cualquier tipo aritmético básico de C# . El único problema es que C# debe saber en el momento de la compilación que las operaciones se realizan en tipos específicos, y parece que escribir un método que agregue de manera eficiente (y transparente) dos números enteros y dos números de punto flotante es imposible.

Especifiquemos nuestros deseos para un método hipotético generalizado que realiza alguna operación matemática simple:

1. Un método debe tener restricciones de tipo generalizadas que nos protegen de intentar agregar (o multiplicar, dividir) dos tipos arbitrarios. Necesitamos alguna restricción de tipo genérico.
2. Para la pureza del experimento, los tipos aceptados y devueltos deben ser los mismos. Por ejemplo, un operador binario debe tener una firma de la forma (T, T) => T
3. El método debe ser al menos parcialmente optimizado. Por ejemplo, el boxeo ubicuo es inaceptable.

¿Y qué hay de los vecinos?

Veamos F# . No soy fuerte en F# , pero la mayoría de las restricciones de C# están dictadas por las limitaciones de CLR , lo que significa que F# sufre los mismos problemas. Puede intentar declarar un método de suma generalizado explícito y el método de suma habitual y ver lo que dice el sistema de inferencia de tipo F# :

 let add_gen (x : 'a) (y : 'a) = x + y let add xy = x + y add_gen 5.0 6.0 |> ignore add 5.0 6.0 |> ignore 

En este caso, ambos métodos resultarán no generalizados y el código generado será idéntico. Dada la rigidez del sistema de tipo F# , donde no hay conversiones implícitas de la forma int -> double , después de la primera llamada de estos métodos con parámetros de tipo double (en términos de C# ), llame a métodos con parámetros de otros tipos (incluso con una posible pérdida de precisión debido a la conversión de tipos) más fallará

Vale la pena señalar que si reemplaza el operador + con el operador de igualdad = , la imagen se vuelve ligeramente diferente : ambos métodos se vuelven generalizados (desde el punto de vista de C# ), y se llama a un método auxiliar especial, disponible en F# para realizar la comparación.

 let eq_gen (x : 'a) (y : 'a) = x = y let eq xy = x = y eq_gen 5.0 6.0 |> ignore eq_gen 5 6 |> ignore eq 5.0 6.0 |> ignore eq 5 6 |> ignore 

¿Qué hay de Java ?

Es difícil para mí hablar de Java , pero, por lo que puedo decir, los tipos significativos no están en la forma habitual para nosotros, pero todavía hay tipos primitivos . Para trabajar con primitivas en Java hay envoltorios (por ejemplo, una referencia Long para primitivo by-value long ), que tienen un Number clase base común. Por lo tanto, puede generalizar parcialmente las operaciones con Number , pero este es un tipo de referencia, que es poco probable que tenga un efecto positivo en el rendimiento.

Corrígeme si me equivoco.

C++ ?

C++ es un lenguaje para tramposos.
C++ allana el camino para características que algunos consideran ... poco naturales .
Las plantillas (también conocidas como plantillas), en contraste con las generalizaciones (genéricos), son, en sentido literal, plantillas . Al declarar una plantilla, puede restringir explícitamente los tipos para los que esta plantilla está disponible. Por esta razón, en C++ , por ejemplo, el siguiente código es válido:

 #include <iostream> template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr> T Add (T left, T right) { return left + right; } int main() { std::cout << Add(5, 6) << std::endl; std::cout << Add(5.0, 6.0) << std::endl; // std::cout << Add("a", "b") << std::endl; Does not compile } 

is_arithmetic , desafortunadamente, permite tanto char como bool como parámetros. Por otro lado, char puede ser equivalente a sbyte en terminología de C# , aunque los tamaños reales de los tipos enteros dependen de la plataforma / compilador / fase lunar.

Lenguajes de escritura dinámica

Finalmente, considere un par de lenguajes dinámicamente escritos (e interpretados ), agudizados por la computación. En tales lenguajes, generalmente la generalización de la computación no causa problemas: si el tipo de parámetros es adecuado para la ejecución, condicionalmente, además, la operación se realizará, de lo contrario fallará con un error.

En Python (3.7.3 x64):

 def add (x, y): return x + y type(add(5, 6)) # <class 'int'> type(add(5.0, 6.0)) # <class 'float'> type(add('a', 'b') # <class 'str'> 

En R (3.6.1 x64)

 add <- function(x, y) x + y # Or typeof() vctrs::vec_ptype_show(add(5, 6)) # Prototype: double vctrs::vec_ptype_show(add(5L, 6L)) # Prototype: integer vctrs::vec_ptype_show(add("5", "6")) # Error in x + y : non-numeric argument to binary operator 

Por el contrario, en el mundo C #: restringimos el tipo generalizado de función matemática

Lamentablemente, no podemos hacer esto. En C# los tipos primitivos son tipos por valor, es decir, estructuras que, aunque se heredan de System.Object (y System.ValueType ), no tienen mucho en común. Una limitación natural y lógica es where T : struct . Comenzando con C# 7.3 tenemos la restricción where T : unmanaged , lo que significa que T es un , null . Además de los tipos aritméticos primitivos que necesitamos, char , bool , decimal , cualquier Enum y cualquier estructura cuyos campos tengan el mismo tipo unmanaged satisfacen estos requisitos. Es decir este tipo pasará la prueba:

 public struct Coords<T> where T : unmanaged { public TX; public TY; } 

Por lo tanto, no podemos escribir una función generalizada que acepte solo los tipos aritméticos deseados. De ahí lo Unsafe en el título del artículo: tendremos que confiar en que los programadores usen nuestro código. Un intento de llamar al método hipotético generalizado T Add<T>(T left, T right) where T : unmanaged conducirá a resultados impredecibles si el programador pasa objetos de un tipo incompatible como argumentos.

El primer experimento, ingenuo: dynamic

dynamic es la primera y obvia herramienta que puede ayudarnos a resolver nuestro problema. Por supuesto, el uso de la dynamic para los cálculos es absolutamente inútil: la dynamic equivalente al object , y el compilador convierte los métodos llamados con una variable dynamic en un reflejo monstruoso. Como beneficio adicional: empacar / desempacar nuestros tipos de valor. Aquí hay un ejemplo :

 public class Class { public static void Method() { var x = Add(5, 6); var y = Add(5.0, 6.0); } private static dynamic Add(dynamic left, dynamic right) => left + right; } 

Solo mire la IL Method Método:

 .method public hidebysig static void Method () cil managed { // Method begins at RVA 0x2050 // Code size 53 (0x35) .maxstack 8 IL_0000: ldc.i4.5 IL_0001: box [System.Private.CoreLib]System.Int32 IL_0006: ldc.i4.6 IL_0007: box [System.Private.CoreLib]System.Int32 IL_000c: call object Class::Add(object, object) IL_0011: pop IL_0012: ldc.r8 5 IL_001b: box [System.Private.CoreLib]System.Double IL_0020: ldc.r8 6 IL_0029: box [System.Private.CoreLib]System.Double IL_002e: call object Class::Add(object, object) IL_0033: pop IL_0034: ret } // end of method Class::Method 

Cargado 5 , empaquetado , cargado 6 , empaquetado, llamado object Add(object, object) .
La opción obviamente no nos conviene.

El segundo experimento, "en la frente"

Bueno, la dynamic no es para nosotros, pero el número de nuestros tipos es finito, y se conocen de antemano. Vamos a armarnos con una palanca de rama y escribirlo: si nuestro tipo es , calculemos algo, de lo contrario, esta es la excepción.

 public static T Add<T>(T left, T right) where T : unmanaged { if(left is int i32Left && right is int i32Right) { // ??? } // ... throw new NotSupportedException(); } 

III, aquí nos encontramos con un problema. Si comprende con qué tipos estamos trabajando, también puede aplicarles la operación, entonces el int condicional resultante debe convertirse a un tipo T desconocido y esto no es muy simple. La return (T)(i32Left + i32Right) no se compila: no hay garantía de que T sea int (aunque sabemos que lo es). Puede probar el return (T)(object)(i32Left + i32Right) conversión doble return (T)(object)(i32Left + i32Right) . Primero, la cantidad se empaca, luego se desempaqueta en T Esto solo funcionará si los tipos coinciden antes del empaque y después del empaque. No puede empaquetar int , pero descomprímalo en double , incluso si hay una conversión implícita int -> double . El problema con este código es la ramificación gigante y la abundancia de paquetes desempacables, incluso en condiciones. Esta opción tampoco es buena.

Reflexión y Metadatos

Bueno, juega y eso es suficiente. Todo el mundo sabe que hay operadores en C# que pueden anularse. Ahí hay + , - , == , == != Y así sucesivamente. Todo lo que tenemos que hacer es extraer un método estático de tipo T correspondiente al operador, por ejemplo, adiciones, eso es todo. Bueno, sí, nuevamente un par de paquetes, pero sin ramificaciones y sin problemas. Todo se puede almacenar en caché por tipo T y, en general, acelerar el proceso en todos los sentidos, reduciendo una operación matemática a llamar a un único método de reflexión. Bueno, algo como esto:

 public static T Add<T>(T left, T right) where T : unmanaged { // Simple example without cache. var method = typeof(T) .GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)}) ?.CreateDelegate(typeof(Func<T, T, T>)) as Func<T, T, T>; return method?.Invoke(left, right) ?? throw new InvalidOperationException(); } 

Lamentablemente esto no funciona . El hecho es que los tipos aritméticos (pero no decimal ) no tienen un método tan estático. Todas las operaciones se implementan a través de operaciones IL , como add . La reflexión normal no resuelve nuestro problema.

System.Linq.Expressions

La solución basada en Expressions se describe en el blog de John Skeet aquí (por Marc Gravell).
La idea es bastante simple. Supongamos que tenemos un tipo T que admite la operación + . Creemos una expresión como esta:

 (x, y) => x + y; 

Después de eso, habiendo almacenado en caché, lo usaremos. Construir tal expresión es bastante fácil. Necesitamos dos parámetros y una operación. Así que vamos a escribirlo.

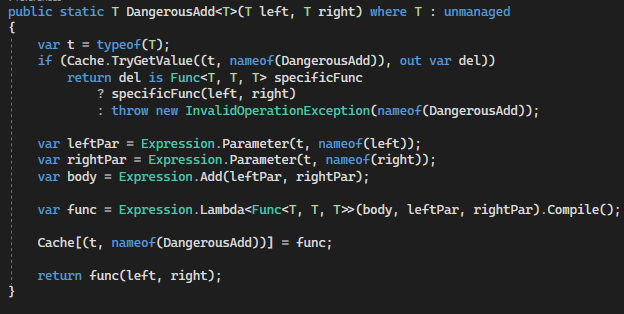
 private static readonly Dictionary<(Type Type, string Op), Delegate> Cache = new Dictionary<(Type Type, string Op), Delegate>(); public static T Add<T>(T left, T right) where T : unmanaged { var t = typeof(T); // If op is cached by type and function name, use cached version if (Cache.TryGetValue((t, nameof(Add)), out var del)) return del is Func<T, T, T> specificFunc ? specificFunc(left, right) : throw new InvalidOperationException(nameof(Add)); var leftPar = Expression.Parameter(t, nameof(left)); var rightPar = Expression.Parameter(t, nameof(right)); var body = Expression.Add(leftPar, rightPar); var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile(); Cache[(t, nameof(Add))] = func; return func(left, right); } 

En el centro se publicó información útil sobre árboles de expresión y delegados.

Técnicamente, las expresiones nos permiten resolver todos nuestros problemas: cualquier operación básica se puede reducir a llamar a un método generalizado. Cualquier operación más compleja se puede escribir de la misma manera, utilizando expresiones más complejas. Esto es casi suficiente.

Rompemos todas las reglas

¿Es posible lograr algo más usando el poder de CLR/C# ? Veamos en qué año se genera el código mediante métodos de adición para diferentes tipos :

 public class Class { public static double Add(double x, double y) => x + y; public static int Add(int x, int y) => x + y; // Decimal only to show difference public static decimal Add(decimal x, decimal y) => x + y; } 

El código IL correspondiente contiene el mismo conjunto de instrucciones:

 ldarg.0 ldarg.1 add ret 

Este es el código operativo add en el que se compila la adición de tipos primitivos aritméticos. decimal en este lugar llama a static decimal decimal.op_Addition(decimal, decimal) . Pero, ¿qué sucede si escribimos un método que se generalizará, pero que contiene exactamente este código IL ? Bueno, John Skeet advierte que esto no vale la pena . En su caso, considera todos los tipos (incluido el decimal ), así como sus análogos nullable . Esto requerirá operaciones IL no triviales y necesariamente conducirá a un error. Pero aún podemos intentar implementar operaciones básicas.

Para mi sorpresa, Visual Studio no contiene plantillas para proyectos IL y archivos IL . No puede simplemente tomar y describir parte del código en IL e incluirlo en su ensamblaje. Naturalmente, el código abierto viene en nuestra ayuda. El proyecto ILSupport contiene plantillas para proyectos IL , así como un conjunto de instrucciones que se pueden agregar a *.csproj para incluir el código IL en el proyecto. Por supuesto, describir todo en IL es bastante difícil, por lo que el autor del proyecto usa el atributo MethodImpl incorporado con el indicador ForwardRef . Este atributo le permite declarar el método como extern y no describir el cuerpo del método. Se parece a esto:

 [MethodImpl(MethodImplOptions.ForwardRef)] public static extern T Add<T>(T left, T right) where T : unmanaged; 

El siguiente paso es escribir la implementación del método en el archivo *.il con el código IL :

 .method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed { .param type [1] .custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor() = (01 00 00 00 ) ldarg.0 ldarg.1 add ret } 

En ninguna parte se refiere explícitamente al tipo !!T , sugerimos que el CLR agregue dos argumentos y devuelva el resultado. No hay controles de tipo, y todo está en la conciencia del desarrollador. Sorprendentemente, funciona, y relativamente rápido.

Un poco de referencia

Probablemente, un punto de referencia honesto se basaría en una expresión bastante compleja, cuyo cálculo "frontal" se compararía con estos peligrosos métodos IL . Escribí un algoritmo simple que resume los cuadrados de números previamente calculados y almacenados en una matriz double y divide la cantidad final por el número de números. Para realizar la operación, utilicé los operadores C# + , * y / , como lo hacen las personas sanas, las funciones creadas con Expressions y las funciones IL .

 BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362 Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=3.1.100 [Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Job-POXTAH : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Runtime=.NET Core 3.1 

Nuestro código inseguro es aproximadamente 2.5 veces más lento (en términos de una operación). Esto se puede atribuir al hecho de que en el caso de un cálculo de "frente", el compilador compila a + b en el código de operación add , y en el caso de un método inseguro, se llama a una función estática, que es naturalmente más lenta.

En lugar de concluir: cuando es true != true

Hace unos días, me encontré con un tweet de Jared Parsons:

Hay casos en los que lo siguiente imprimirá "falso"
bool b = ...
if (b) Console.WriteLine (b.IsTrue ());

Esta fue la respuesta a esta entrada , que muestra el código de verificación de bool para true , que se parece a esto:

 public static bool IsTrue(this bool b) { if (b == true) return true; else if (b == false) return false; else return !true && !false; } 

Los cheques parecen redundantes, ¿verdad? Jared da un contraejemplo que demuestra algunas de las características del comportamiento bool . La idea es que bool es byte ( sizeof(bool) == 1 ), mientras que false coincide con 0 y true coincide con 1 . Siempre y cuando no balancees los punteros, bool comporta de manera inequívoca y previsible. Sin embargo, como ha demostrado Jared, puede crear un bool usando 2 como valor inicial, y algunas de las comprobaciones fallarán correctamente:

 bool b = false; byte* ptr = (byte*)&b; *ptr = 2; 

Podemos lograr un efecto similar usando nuestras operaciones matemáticas inseguras (esto no funciona con Expressions ):

 var fakeTrue = Subtract<bool>(false, true); var val = *(byte*)&fakeTrue; if(fakeTrue) Assert.AreNotEqual(fakeTrue, true); else Assert.Fail("Clause not entered."); 

Sí, sí, verificamos dentro de la rama true si la condición es true y esperamos que, de hecho, no sea true . ¿Por qué es esto así? Si resta de 0 ( =false ) 1 ( =true ) sin comprobaciones, para el byte será igual a 255 . Naturalmente, 255 (nuestro fakeTrue ) no es 1 (verdadero true ), por lo que se ejecuta fakeTrue . La ramificación funciona de manera diferente.

if produce inversión: se inserta una rama condicional; si la condición es falsa , se produce una transición al punto después del final del bloque if . La validación se realiza mediante la brfalse_S brfalse / brfalse_S . Compara el último valor en la pila con cero . Si el valor es cero, entonces es false , pasamos por encima del bloque if . En nuestro caso, fakeTrue simplemente no es igual a cero, por lo que la verificación pasa y la ejecución continúa dentro del bloque if , donde comparamos fakeBool con el valor verdadero y obtenemos un resultado negativo.

UPD01:
Después de discutir en los comentarios con shai_hulud y blowin , agregué otro método a los puntos de referencia que implementa una rama como if(typeof(T) == typeof(int)) return (T)(object)((int)(object)left + (int)(object)right); . A pesar del hecho de que JIT debería optimizar las comprobaciones, al menos cuando T es una struct , dichos métodos aún funcionan un orden de magnitud más lento. No es obvio si las transformaciones T -> int -> T optimizadas, o si se usa boxing / unboxing. Los resultados del punto de referencia MethodImpl ven afectados significativamente por los indicadores MethodImpl .

UPD02:
xXxVano en los comentarios mostró un ejemplo de uso de ramificación por tipo y convierte T <--> un tipo específico usando Unsafe.As<TFrom, TTo>() . Por analogía con la ramificación habitual y el object personalizado personalizado, escribí tres operaciones (suma, multiplicación y división) con ramificación para todos los tipos aritméticos, después de lo cual agregué otro punto de referencia ( UnsafeBranchSum ). A pesar del hecho de que todos los métodos (excepto las expresiones) generan un código ASM casi idéntico (hasta donde mi limitado conocimiento del ensamblador me permite juzgar), por alguna razón desconocida, ambos métodos con ramificación son muy lentos en comparación con la suma directa ( DirectSum ) y utilizando genéricos y código IL . No tengo ninguna explicación para este efecto, el hecho de que el tiempo dedicado crece proporcionalmente a N indica que hay algún tipo de sobrecarga constante para cada operación, a pesar de toda la magia de JIT . Falta esta sobrecarga en la versión IL de los métodos. , IL - , / / , 100% ( , ).
, , - .