
Las computadoras cuánticas y la computación cuántica son una nueva palabra de moda que se ha agregado a nuestro espacio de información junto con inteligencia artificial , aprendizaje automático y otros términos de alta tecnología. Al mismo tiempo, no pude encontrar material en Internet que pusiera en mi cabeza un rompecabezas llamado "cómo funcionan las computadoras cuánticas" . Sí, hay muchos trabajos excelentes, incluso en el Habré (ver la Lista de recursos ), los comentarios sobre los cuales, como suele suceder, son aún más informativos y útiles, pero la imagen en la cabeza, como dicen, no cuadró.
Y recientemente, mis colegas se me acercaron y me preguntaron: “¿Entiendes cómo funciona una computadora cuántica? ¿Puedes decirnos? ”Y luego me di cuenta de que el problema de doblar una imagen completa en mi cabeza no es solo mío.
Como resultado, se intentó compilar información sobre computadoras cuánticas en un esquema lógico consistente en el cual, en un nivel básico, sin una inmersión profunda en las matemáticas y la estructura del mundo cuántico , se explicó qué era una computadora cuántica, en qué principios funcionaba y también qué problemas enfrentaba científicos en su creación y operación.
Tabla de contenidos
Descargo de responsabilidad
(al contenido)
El autor no es un especialista en computación cuántica, y el público objetivo del artículo son los mismos expertos en TI, no especialistas cuánticos , que también quieren poner en su cabeza una imagen llamada "Cómo funcionan las computadoras cuánticas". Debido a esto, muchos conceptos en el artículo se simplifican deliberadamente para una mejor comprensión de las tecnologías cuánticas en el nivel "básico", pero sin mucha simplificación con la pérdida de contenido de información y su adecuación .
En algunos lugares, el artículo utiliza materiales de otras fuentes, cuya lista se encuentra al final del artículo . Siempre que sea posible, se insertan enlaces directos y referencias al texto original, tabla o imagen. Si en algún lugar olvidé algo (o alguien), escribe: lo corregiré.
Introduccion
(al contenido)
En este capítulo, veremos brevemente cómo comenzó la era cuántica, que fue la motivación para la idea de una computadora cuántica, que (qué países y corporaciones) son actualmente los principales actores en este claro, y hablaremos brevemente sobre las principales direcciones de desarrollo de la computación cuántica.
Como empezó todo
(al contenido)

Se considera que el punto de referencia de la era cuántica es 1900, cuando M. Planck presentó por primera vez la hipótesis de que la energía se emite y se absorbe no continuamente, sino en cuantos (porciones) separados. La idea fue recogida y desarrollada por muchos científicos destacados de la época: Bohr, Einstein, Heisenberg, Schrödinger, lo que, en última instancia, condujo a la creación y desarrollo de una ciencia como la física cuántica . Hay muchos buenos materiales sobre el desarrollo de la física cuántica como ciencia en la Web. En este artículo no nos detendremos en detalle, pero fue necesario indicar la fecha en que entramos en la nueva era cuántica.
La física cuántica ha traído a nuestra vida ordinaria muchos inventos y tecnologías, sin los cuales ahora es difícil imaginar el mundo que nos rodea. Por ejemplo, un láser, que ahora se usa en todas partes, desde electrodomésticos (niveles láser, etc.) hasta sistemas de alta tecnología (láser de corrección de visión, hola meklon ). Sería lógico suponer que tarde o temprano alguien presentará la idea de por qué no utilizar sistemas cuánticos para los cálculos. Y así en 1980 sucedió.
Wikipedia indica que el científico Yuri Manin fue el primero en expresar la idea de la computación cuántica en 1980. Pero realmente comenzaron a hablar de eso solo en 1981, cuando el conocido R. Feynman, en su informe en la primera conferencia sobre física computacional celebrada en el Instituto de Tecnología de Massachusetts , señaló que es imposible modelar la evolución de un sistema cuántico en una computadora clásica de una manera efectiva. Propuso un modelo elemental de una computadora cuántica que podría realizar tal simulación.
Existe un trabajo en la Web en el que la cronología del desarrollo de la computación cuántica se considera de manera más académica y detallada, pero veremos brevemente:
Hitos en la historia de las computadoras cuánticas:
Como puede ver, han pasado 17 años (de 1981 a 1998) desde el momento de la idea hasta su primera implementación en una computadora con 2 qubits, y 21 años (de 1998 a 2019) hasta el momento en que el número de qubits aumentó a 53. Tomó 11 años (de 2001 a 2012) mejorar el resultado del algoritmo Shore (nos detendremos un poco más) del número 15 al 21. Además, solo hace tres años nos dimos cuenta de lo que hablaba Feynman, y aprende a simular los sistemas físicos más simples.
El desarrollo de la computación cuántica es lento. Los científicos e ingenieros se enfrentan a tareas muy complejas, los estados cuánticos son muy efímeros y frágiles, y para mantenerlos el tiempo suficiente para realizar los cálculos, uno tiene que construir sarcófagos por decenas de millones de dólares, en los que la temperatura se mantiene justo por encima del cero absoluto, y que están protegidos de influencias externas Además, hablaremos sobre estas tareas y problemas con más detalle.
Jugadores destacados
(al contenido)

Las diapositivas de esta sección están tomadas del artículo Quantum Computer: A Big Boost Game. Conferencia en Yandex , de un investigador en el Centro Cuántico Ruso Alexei Fedorov. Me permitiré citas directas:
Todos los países tecnológicamente exitosos participan actualmente activamente en el desarrollo de tecnologías cuánticas. Se invierte una gran cantidad de dinero en estos estudios, se están creando programas especiales para apoyar las tecnologías cuánticas.

La carrera cuántica involucra no solo estados, sino también empresas privadas. En total, Google, IBM, Intel y Microsoft han invertido alrededor de $ 0.5 mil millones en el desarrollo de computadoras cuánticas en los últimos años, crearon grandes laboratorios y centros de investigación.
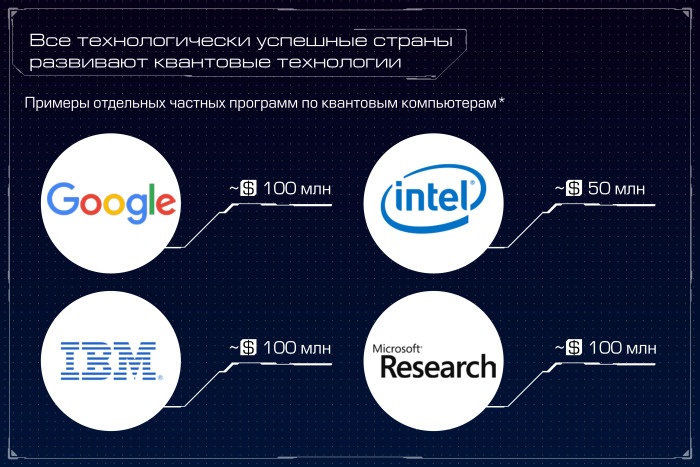
Hay muchos artículos sobre Habré y en la Web, por ejemplo, aquí , aquí y aquí , en los que se considera con más detalle el estado actual de las cosas con el desarrollo de tecnologías cuánticas en diferentes países. Para nosotros ahora, lo principal es que todos los principales países y jugadores tecnológicamente avanzados invierten enormes cantidades de dinero en investigación en esta dirección, lo que brinda la esperanza de una salida del actual estancamiento tecnológico.
Direcciones de desarrollo
(al contenido)

En este momento (puedo estar equivocado, correcto) los esfuerzos principales (y resultados más o menos significativos) para todos los jugadores principales se concentran en dos direcciones:
- Computadoras cuánticas especializadas que tienen como objetivo resolver un problema específico específico, por ejemplo, problemas de optimización. Un ejemplo de un producto son las computadoras cuánticas D-Wave.
- Computadoras cuánticas universales : que pueden implementar algoritmos cuánticos arbitrarios (Shore, Grover, etc.). Implementaciones de IBM, Google.
Otros vectores de desarrollo que nos proporciona la física cuántica, como:
ciertamente también en la lista de áreas de investigación, pero actualmente parece haber algún tipo de resultados más o menos significativos.
Además, puede leer la hoja de ruta para el desarrollo de tecnologías cuánticas , bueno, google " desarrollo de tecnologías cuánticas ", por ejemplo, aquí , aquí y aquí .
Lo basico. Objeto cuántico y sistemas cuánticos
(al contenido)

Lo más importante que debes entender de esta sección es que
Una computadora cuántica (a diferencia de una convencional) utiliza objetos cuánticos como portadores de información, y los objetos cuánticos deben estar conectados a un sistema cuántico para realizar los cálculos.
¿Qué es un objeto cuántico?
Un objeto cuántico es un objeto del micromundo (mundo cuántico) que exhibe propiedades cuánticas:
- Tiene un cierto estado con dos niveles límite.
- Está en una superposición de su estado hasta el momento de la medición.
- Enredados con otros objetos para crear sistemas cuánticos
- Realiza un teorema de prohibición de clonación (no puede copiar el estado de un objeto)
Analicemos cada propiedad con más detalle:
Tiene un cierto estado con dos niveles límite (estado final)
Un ejemplo clásico del mundo real es una moneda. Ella tiene un estado de "lado", que tiene dos niveles límite: "águila" y "colas".
Está en una superposición de su estado hasta el momento de la medición.
Lanzó una moneda, vuela y gira. Mientras está girando, es imposible decir en cuál de los niveles límite se encuentra su estado "lateral". Pero si lo cerramos de golpe y miramos el resultado, la superposición de estados colapsa inmediatamente en uno de los dos límites: "cabezas" y "colas". Golpear una moneda en nuestro caso es una dimensión.
Enredados con otros objetos para crear sistemas cuánticos
Es difícil con una moneda, pero lo intentaremos. Imagina que lanzamos tres monedas para que giren aferradas entre sí, como un malabarismo de monedas. En cada momento, no solo cada uno de ellos está en una superposición de estados, sino que estos estados se influencian mutuamente (las monedas chocan).
Realiza un teorema de prohibición de clonación (no puede copiar el estado de un objeto)
Mientras las monedas están volando y girando, de ninguna manera podemos crear una copia del estado de rotación de ninguna de las monedas separadas del sistema. El sistema vive en sí mismo y está muy celoso de dar cualquier información.
Un par de palabras sobre el concepto mismo de "superposición" , en casi todos los artículos, la superposición se explica como "está en todos los estados al mismo tiempo", lo cual, por supuesto, es cierto, pero a veces es demasiado confuso. Una superposición de estados también se puede considerar como el hecho de que en cada momento un objeto cuántico tiene ciertas probabilidades de colapsar en cada uno de sus niveles límite, y en total estas probabilidades son naturalmente iguales a 1 . Además, al considerar el qubit, nos detendremos en esto con más detalle.
Para las monedas, esto se puede imaginar visualmente, dependiendo de la velocidad inicial, el ángulo del lanzamiento, el estado del entorno en el que vuela la moneda, en cada momento la probabilidad de obtener un "águila" o "colas" es diferente. Y, como se mencionó anteriormente, el estado de dicha moneda voladora puede imaginarse como "está en todos sus estados límite al mismo tiempo, pero con una probabilidad diferente de su implementación".
Cualquier objeto para el que se satisfagan las propiedades anteriores y que podamos crear y administrar se puede utilizar como medio de almacenamiento en una computadora cuántica.
Un poco más adelante, hablaremos sobre el estado actual de las cosas con la implementación física de qubits como objetos cuánticos, y lo que los científicos están utilizando ahora en esta capacidad.
Entonces, la tercera propiedad dice que los objetos cuánticos pueden enredarse para crear sistemas cuánticos. ¿Qué es un sistema cuántico?
Un sistema cuántico es un sistema de objetos cuánticos enredados con las siguientes propiedades:
- Un sistema cuántico está en una superposición de todos los estados posibles de los objetos en los que consiste
- Es imposible conocer el estado del sistema hasta el momento de la medición.
- En el momento de la medición, el sistema implementa una de las posibles variantes de sus estados límite
(y corriendo un poco por delante)
Corolario de los programas cuánticos :
- Un programa cuántico tiene un estado dado del sistema en la entrada, una superposición en el interior, una superposición en la salida
- En la salida del programa después de la medición, tenemos una implementación probabilística de uno de los posibles estados finales del sistema (más posibles errores)
- Cualquier programa cuántico tiene una arquitectura de chimenea (entrada -> salida. No hay ciclos, no puede ver el estado del sistema en el medio del proceso).
Comparación de una computadora cuántica y una convencional
(al contenido)

Ahora comparemos una computadora convencional con una cuántica.
Nivel lógico

En una computadora normal, esto es un poco. Un bit determinista bien conocido de principio a fin. Puede tomar valores 0 o 1. Se adapta bien al papel de una unidad lógica para una computadora normal, pero es completamente inadecuado para describir el estado de un objeto cuántico , que, como ya hemos dicho, está en estado salvaje con la asunción de sus estados límite .
Para esto, se inventó un qubit . En sus estados límite, se da cuenta de los estados | 0> y | 1> similares a 0 y 1, y en superposición representa una distribución de probabilidad sobre sus estados límite |0> y |1> :
a|0> + b|1>, , a^2+b^2=1
en este caso, ayb representan las amplitudes de las probabilidades , y los cuadrados de sus módulos representan las probabilidades, de hecho, para obtener con precisión tales valores de los estados límite |0> y |1>, si el qubit está colapsado por la medición en este momento.
Nivel fisico
En el nivel tecnológico actual de desarrollo, la implementación física de un bit para una computadora normal es un transistor semiconductor , para un objeto cuántico, como hemos dicho, cualquier objeto cuántico . En la siguiente sección, hablaremos sobre lo que ahora se usa como portadores físicos de qubits.
Medio de almacenamiento
Para una computadora normal, esta es una corriente eléctrica : niveles de voltaje, presencia o ausencia de corriente, etc., para una cuántica: el estado mismo de un objeto cuántico (dirección de polarización, giro, etc.), que puede estar en un estado de superposición.
Operaciones
Para implementar circuitos lógicos en una computadora normal, todos usamos operaciones lógicas bien conocidas; para las operaciones en qubits, tuvimos que idear un sistema de operaciones completamente diferente llamado puertas cuánticas . Las puertas son de un solo qubit y dos qubit, dependiendo de cuántos qubits se conviertan.
Ejemplos de puertas cuánticas:
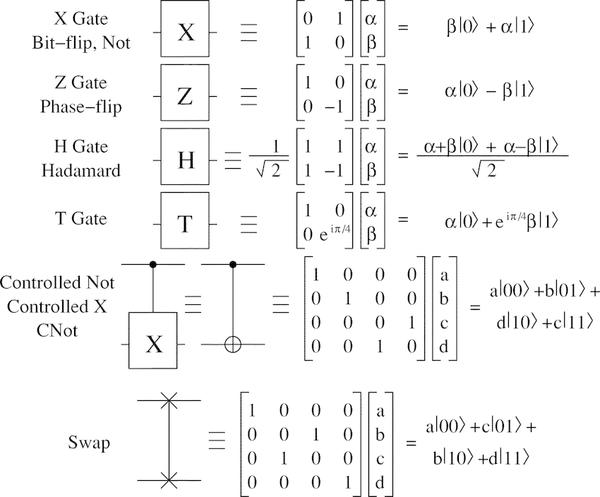
Existe el concepto de un conjunto universal de puertas , que son suficientes para realizar cualquier cálculo cuántico. Por ejemplo, un conjunto universal incluye una válvula Hadamard, una válvula de cambio de fase, una válvula CNOT y una válvula π⁄8. Con su ayuda, puede realizar cualquier cálculo cuántico en un conjunto arbitrario de qubits.
En este artículo no nos detendremos en detalle en el sistema de puertas cuánticas; en más detalle sobre ellas y las operaciones lógicas en qubits se pueden leer, por ejemplo, aquí . Lo principal para recordar:
- Las operaciones en objetos cuánticos requieren la creación de nuevos operadores lógicos (puertas cuánticas)
- Las válvulas cuánticas son de un solo qubit y dos qubit
- Existen conjuntos de puertas universales con los que puede realizar cualquier cálculo cuántico.
Interconexión
Un transistor es completamente inútil para nosotros, para hacer los cálculos necesitamos conectar muchos transistores entre sí, es decir, crear un chip semiconductor a partir de millones de transistores, en el que ya construimos circuitos lógicos, ALU y, en última instancia, obtener un procesador moderno en su forma clásica.
Un qubit también es completamente inútil para nosotros (bueno, aunque solo sea en términos académicos),
para hacer cálculos necesitamos un sistema de qubits (objetos cuánticos)
que, como ya dijimos, se crea entrelazando qubits entre ellos para que los cambios en sus estados ocurran en concierto.
Algoritmos
Los algoritmos estándar que la humanidad ha acumulado hasta el momento actual son completamente inadecuados para la implementación en una computadora cuántica. Sí, en general, y no hay necesidad. Las computadoras cuánticas basadas en la lógica de puerta sobre qubits requieren la creación de algoritmos completamente diferentes, algoritmos cuánticos. De los algoritmos cuánticos más famosos, se pueden distinguir tres:
Principio
Y la diferencia más importante es el principio del trabajo. Para una computadora estándar, este es un principio digital estrictamente determinado , basado en el hecho de que si establecemos un estado inicial del sistema y lo pasamos a través de un algoritmo dado, el resultado de los cálculos será el mismo, sin importar cuántas veces ejecutemos este cálculo. En realidad, este comportamiento es exactamente lo que esperamos de la computadora.
Una computadora cuántica funciona con un principio analógico y probabilístico . El resultado de un algoritmo dado en un estado inicial dado es una muestra de la distribución de probabilidad de las implementaciones finales del algoritmo más posibles errores.
Esta naturaleza probabilística de la computación cuántica se debe a la esencia muy probabilística del mundo cuántico. "Dios no juega a los dados con el universo ", dijo el viejo Einstein, pero todos los experimentos y observaciones hasta ahora (en el paradigma científico actual) confirman lo contrario.
Implementaciones físicas de qubits.
(al contenido)

Como ya dijimos, un qubit puede ser representado por un objeto cuántico, es decir, un objeto físico que implementa las propiedades cuánticas descritas anteriormente. Es decir, más o menos, cualquier objeto físico en el que hay dos estados y estos dos estados se encuentran en un estado de superposición se puede utilizar para construir una computadora cuántica.
“Si podemos poner un átomo en dos niveles diferentes y controlarlos, entonces aquí hay un qubit para ti. Si podemos hacer esto con un ion, qubit. Es lo mismo con la corriente. Si lo ejecutamos en sentido horario y antihorario al mismo tiempo, aquí hay un qubit ”. (C)
Hay un comentario maravilloso sobre el artículo en el que la variedad actual de realizaciones físicas del qubit se considera con más detalle, pero solo enumeramos los más famosos y comunes:
De toda esta diversidad, el primer método para producir qubits basado en superconductores es el más elaborado. Google , IBM , Intel y otros jugadores líderes lo usan para construir sus sistemas.
Bueno, también lea la revisión de posibles realizaciones físicas de qubits de Andrew Daley, 2014 .
Lo basico. El principio de funcionamiento de una computadora cuántica
(al contenido)

Los materiales para esta sección (tarea e imágenes) están tomados del artículo "Casi sobre el complejo. Cómo funciona una computadora cuántica " .
Entonces, imaginemos que tenemos la siguiente tarea:
Hay un grupo de tres personas: (A) ndrey, (B) olodya y (C) herejía . Hay dos taxis (0 y 1) .
También se sabe que:
- (A) ndrey, (B) olodya - amigos
- (A) ndrey, (C) herejía - enemigos
- (B) olodya y (C) herejía - enemigos
Tarea: colocar a las personas en taxi para que Max (amigos) y Min (enemigos)
Puntuación: L = (número de amigos) - (número de enemigos) para cada opción de alojamiento
IMPORTANTE: Suponga que no hay heurística, no hay una solución óptima. En este caso, el problema se resuelve solo mediante una búsqueda exhaustiva de opciones.
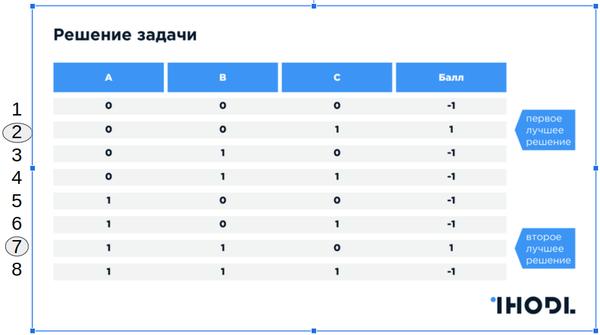
Solución en una computadora normal
Cómo resolver este problema en una computadora (súper) regular (o clúster): está claro que necesitamos clasificar todas las opciones posibles en un bucle . Si tenemos un sistema multiprocesador, podemos paralelizar el cálculo de soluciones en varios procesadores y luego recopilar los resultados.
Tenemos 2 opciones de alojamiento posibles (taxi 0 y taxi 1) y 3 personas. El espacio de soluciones es 2 ^ 3 = 8 . Puede pasar por 8 opciones incluso en una calculadora, esto no es un problema. Y ahora complicaremos la tarea: tenemos 20 personas y dos autobuses, el espacio de solución es 2 ^ 20 = 1,048,576 . Nada demasiado complicado. Aumentemos el número de personas en 2.5 veces: tome 50 personas y dos trenes, el espacio de decisión ahora es 2 ^ 50 = 1.12 x 10 ^ 15 . Una computadora (súper) normal ya está comenzando a tener serios problemas. Aumentaremos el número de personas 2 veces, 100 personas nos darán 1.2 x 10 ^ 30 opciones posibles.
Todo, en un tiempo razonable, esta tarea no se puede contar.
Conectamos una supercomputadora
La computadora más poderosa actualmente es la número 1 del Top500 , es Summit , con una capacidad de 122 Pflops . Supongamos que para el cálculo de una opción, 100 operaciones son suficientes para nosotros, luego para resolver el problema para 100 personas necesitamos:
(1.2 x 10 ^ 30100) / 122x10 ^ 15 / (60 60 24 365) = 3 x 10 ^ 37 años.
Como vemos, cuando aumenta la dimensión de los datos de origen, el espacio de solución crece de acuerdo con una ley de potencia , en el caso general de N bits tenemos 2 ^ N posibles soluciones que, con N relativamente pequeño (100), nos dan un espacio ilegible (en el nivel tecnológico actual) decisiones
¿Hay alguna alternativa? Como habrás adivinado, sí, la hay.
Pero antes de pasar a cómo y por qué las computadoras cuánticas pueden resolver eficazmente tales problemas, recordemos un poco sobre qué es una distribución de probabilidad . No se alarme, el artículo de revisión, no habrá matemáticas difíciles aquí, nos las arreglaremos con un ejemplo clásico con una bolsa y pelotas.
Bastante un poco de combinatoria, teoría de la probabilidad y un extraño experimentador
Tome una bolsa y ponga 1000 bolas blancas y 1000 bolas negras . Llevaremos a cabo un experimento: saque la pelota, escriba el color, devuelva la pelota a la bolsa y mezcle las bolas en la bolsa.
Realizamos el experimento 10 veces, sacamos 10 bolas negras . Tal vez? Bastante ¿Esta muestra nos da algún concepto razonable de la verdadera distribución en la bolsa? Obviamente no. Lo que debe hacer es correcto, repetir el experimento un millón de veces y calcular la frecuencia de la caída de bolas blancas y negras. Obtenemos, por ejemplo, 49.95% de negro y 50.05% de blanco . En este caso, la estructura de distribución de la que tomamos muestras ya está más o menos clara (tomamos una bola).
Lo principal que debe comprender es que el experimento en sí es de naturaleza probabilística , con una muestra (bola) no reconocemos la verdadera estructura de distribución, necesitamos repetir el experimento muchas veces y promediar los resultados.
Agregue 10 bolas rojas y 10 verdes a nuestra bolsa (errores). Repite el experimento 10 veces. En tirado 5 rojos y 5 verdes . Tal vez? Si Podemos decir algo sobre la verdadera distribución - No. Lo que hay que hacer, bueno, ya entiendes.
Para comprender la estructura de la distribución de probabilidad, es necesario muestrear repetidamente los resultados individuales de esta distribución y promediar los resultados.
Conectamos teoría con práctica
Ahora, en lugar de bolas blancas y negras, tomemos las bolas de billar y pongamos en la bolsa 1000 bolas con el número 2, 1000 con el número 7 y 10 bolas con otros números . Imagine a un experimentador que está entrenado en pasos simples (obtener una pelota, anotar el número, volver a poner la pelota en la bolsa, mezclar las bolas en la bolsa) y lo hace en 150 microsegundos. Bueno, tal experimentador en ayudas (no publicidad de drogas !!!). Luego, en 150 segundos, podrá realizar nuestro experimento 1 millón de veces y proporcionarnos los resultados del promedio.
Sentaron al experimentador, le dieron la bolsa, se dieron la vuelta, esperaron 150 segundos y recibieron:
número 2 - 49.5%, número 7 - 49.5%, los números restantes en la cantidad - 1%.
Sí, es cierto, nuestra bolsa es una computadora cuántica con un algoritmo que resuelve nuestro problema , y las bolas son posibles soluciones. Dado que hay dos soluciones correctas, una computadora cuántica nos dará con la misma probabilidad cualquiera de estas posibles soluciones y 0.5% de errores (10/2000) , de los que hablaremos más adelante.
Para obtener el resultado de una computadora cuántica, debe ejecutar el algoritmo cuántico repetidamente en el mismo conjunto de datos de entrada y promediar el resultado.
Escalabilidad de una computadora cuántica
Ahora imaginemos que para un problema en el que participan 100 personas (recordamos este espacio de decisión 2 ^ 100 ), solo hay dos soluciones correctas. Luego, si tomamos 100 qubits y escribimos un algoritmo que calcula nuestra función objetivo (L, ver arriba) sobre estos qubits, entonces obtenemos una bolsa que contiene 1000 bolas con el número de la primera respuesta correcta, 1000 con el número de la segunda respuesta correcta y 10 bolas con otros numeros. Y nuestro experimentador en los mismos 150 segundos nos dará una estimación de la distribución probabilística de las respuestas correctas .
El tiempo de ejecución del algoritmo cuántico (con algunos supuestos) puede considerarse constante O (1) con respecto a la dimensión del espacio de solución (2 ^ N).
Y es precisamente esta propiedad de una computadora cuántica: la constancia del tiempo de ejecución con respecto a la complejidad del espacio de decisión que crece de acuerdo con la ley de poder es la clave.
Qubit y mundos paralelos
¿Cómo sucede esto? ¿Qué le permite a una computadora cuántica hacer cálculos tan rápido? Se trata de la naturaleza cuántica de qubit.
Mire, dijimos que un qubit como objeto cuántico se da cuenta de uno de sus dos estados cuando se observa , pero en la "naturaleza viva" está en una superposición de estados , es decir, está en sus dos estados límite al mismo tiempo (con cierta probabilidad).
Tome (A) Ndrey e imagine su condición (en la cual el vehículo es 0 o 1) como un qubit. Luego tenemos (en un espacio cuántico) dos mundos paralelos , en uno (A) sentado en un taxi 0, en otro mundo - en un taxi 1. Al mismo tiempo en dos taxis , pero con alguna posibilidad de encontrarlo en cada uno de ellos al observar.
Tome (B) olod y también imagine su estado como un qubit. Surgen otros dos mundos paralelos. Pero mientras estos pares de mundos (A) y (B) no interactúan de ninguna manera. ¿Qué se debe hacer para crear un sistema conectado ? Así es, debes conectar (confundir) estos qubits. Tomamos y confundimos (A) con (B) : obtenemos un sistema cuántico de dos qubits (A, B), que implementa cuatro mundos paralelos interdependientes dentro de sí mismo. Agregue (C) erge y obtenga un sistema de tres qubits (ABC), que implementa ocho mundos paralelos interdependientes .
La esencia de la computación cuántica (la implementación de una cadena de puertas cuánticas sobre un sistema de qubits acoplados) es el hecho de que el cálculo se lleva a cabo en todos los mundos paralelos simultáneamente.
Y no importa cuántos de ellos tengamos, 2 ^ 3 o 2 ^ 100, el algoritmo cuántico se ejecutará en un tiempo finito en todos estos mundos paralelos y nos dará el resultado, que es una muestra de la distribución de probabilidad de las respuestas del algoritmo.
Para una mejor comprensión, podemos imaginar que una computadora cuántica a nivel cuántico inicia procesos de decisión paralelos 2 ^ N , cada uno de los cuales trabaja en una opción posible, luego recopila los resultados del trabajo y nos da la respuesta en forma de superposición de la solución (distribución de probabilidad de respuestas), desde que muestreamos una vez cada vez (en cada experimento).
Recuerde el tiempo que le toma a nuestro experimentador (150 μs) llevar a cabo el experimento, esto será útil un poco más cuando hablemos sobre los principales problemas de las computadoras cuánticas y el tiempo de decoherencia.
Algoritmos cuánticos
(al contenido)
Como ya se mencionó, los algoritmos convencionales basados en lógica binaria no son aplicables a una computadora cuántica que usa lógica cuántica (compuertas cuánticas). Para él, tuvo que idear otros nuevos que aprovechen al máximo el potencial inherente a la naturaleza cuántica de la informática.
Los algoritmos más famosos de la actualidad son:
A diferencia de los clásicos, las computadoras cuánticas no son universales.
Hasta ahora, solo se ha encontrado un pequeño número de algoritmos cuánticos. (C)
Gracias a oxoron por el enlace al Zoológico de Algoritmo Cuántico , el lugar donde, según el autor ( Stephen Jordan ), los mejores representantes del mundo cuántico-algorítmico se reúnen y continúan reuniéndose.
En este artículo no analizaremos los algoritmos cuánticos en detalle, hay muchos materiales excelentes en la Web para cualquier nivel de complejidad, pero aún debe repasar brevemente los tres más famosos.
Algoritmo de orilla.
(al contenido)
El algoritmo cuántico más famoso es el algoritmo Shor (inventado en 1994 por el matemático inglés Peter Shor ), cuyo objetivo es resolver el problema de descomponer los números en factores primos (el problema de factorización, el logaritmo discreto).
Este algoritmo se usa como ejemplo cuando escriben que sus sistemas bancarios y contraseñas serán pirateados pronto. Teniendo en cuenta que la longitud de las claves utilizadas hoy en día no es inferior a 2048 bits, aún no ha llegado el momento del límite.
Hasta la fecha, los resultados son más que modestos. Los mejores resultados de factorización con el algoritmo Shore son los números 15 y 21 , que son mucho menos de 2048 bits. Para los resultados restantes de la tabla, se utilizó un algoritmo de cálculo diferente, pero incluso el mejor resultado según este algoritmo (291311) está lejos de ser una aplicación real.
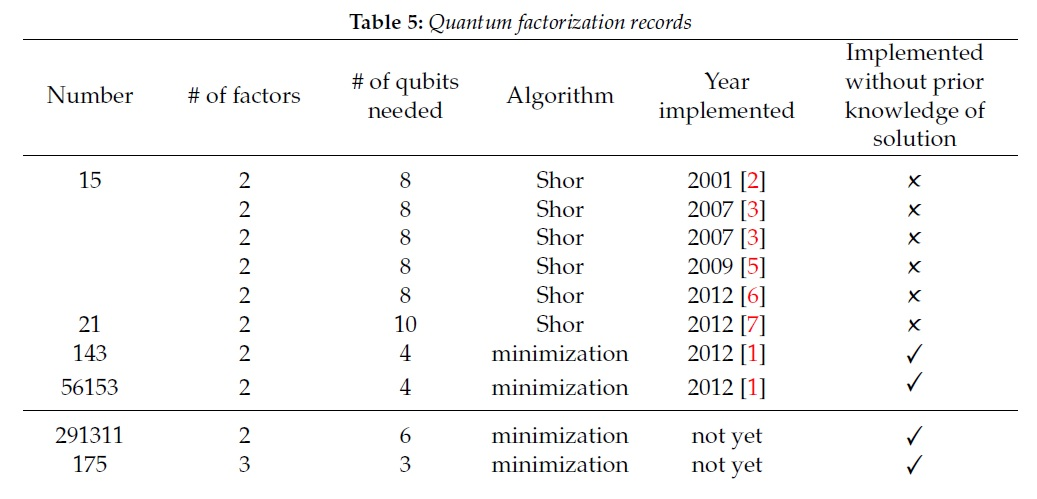
Puede leer más sobre el algoritmo Shore, por ejemplo, aquí . Sobre la implementación práctica - aquí .
Una de las estimaciones actuales de complejidad y potencia necesarias para factorizar un número de 2048 bits es una computadora con 20 millones de qubits . Dormimos en paz
Algoritmo de Grover
(al contenido)
El algoritmo de Grover es un algoritmo cuántico para resolver el problema de enumeración, es decir, encontrar una solución a la ecuación F(X) = 1 , donde F es una función booleana de n variables. Fue propuesto por el matemático estadounidense Lov Grover en 1996 .
El algoritmo de Grover se puede usar para encontrar la mediana y la media aritmética de una serie numérica. Además, se puede utilizar para resolver problemas de NP completo al buscar exhaustivamente entre las muchas soluciones posibles. Esto puede conducir a un aumento significativo de la velocidad en comparación con los algoritmos clásicos, aunque sin proporcionar una " solución polinómica " en general . (C)
Puedes leer más aquí o aquí . También hay una buena explicación del algoritmo en el ejemplo de las cajas y la pelota, pero, desafortunadamente, por razones fuera de mi control, este sitio no me abre desde Rusia. Si su sitio también está bloqueado, aquí hay un breve resumen:
Algoritmo de Grover. Imagine que tiene N piezas de cajas cerradas numeradas. Todos están vacíos, excepto en el que se encuentra la pelota. Su tarea: averiguar el número del cuadro en el que se encuentra la pelota (este número desconocido a menudo se denota con la letra w).

¿Cómo resolver este problema? , , . , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
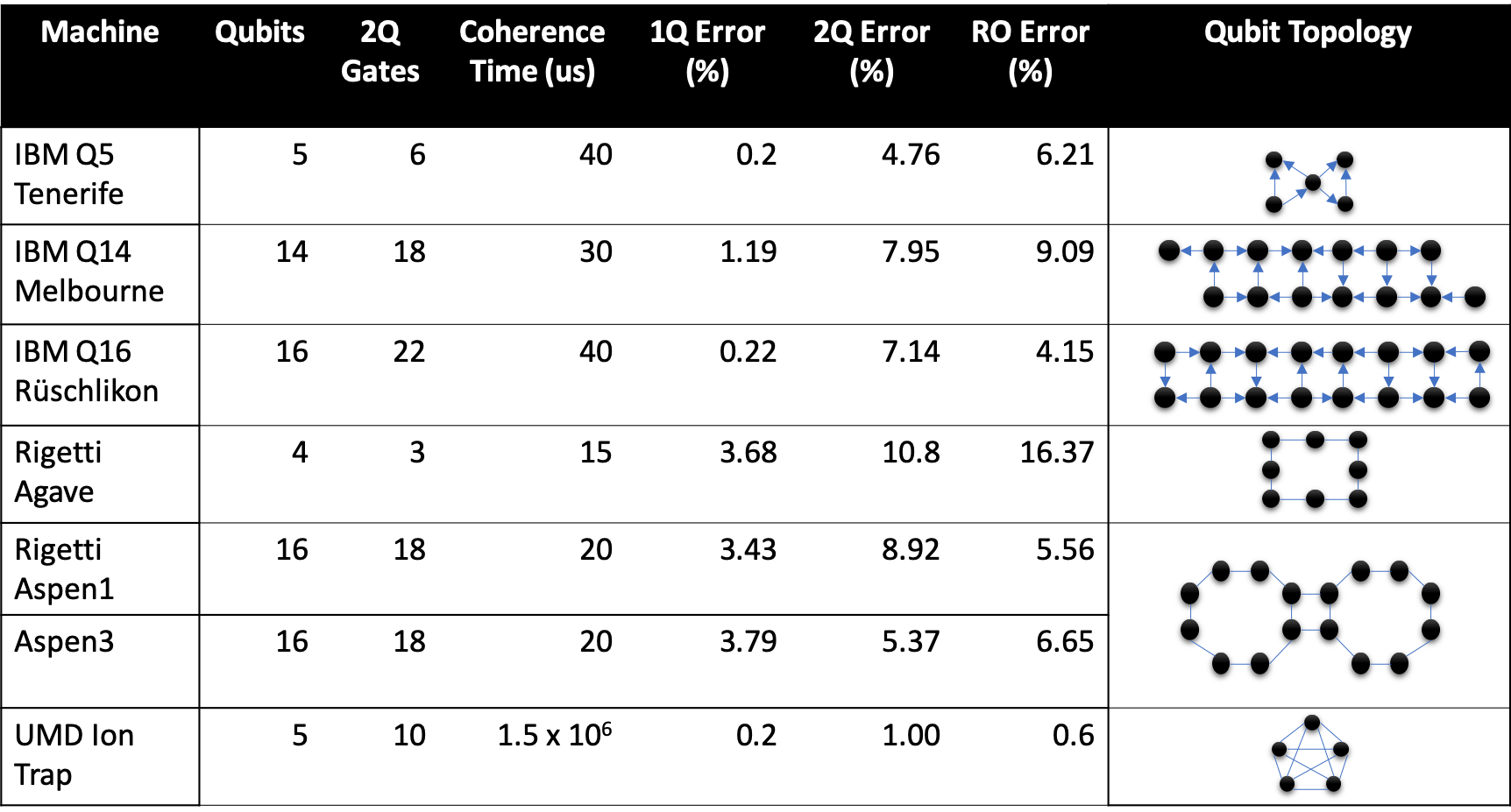
:
( )
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
( )

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
( )

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
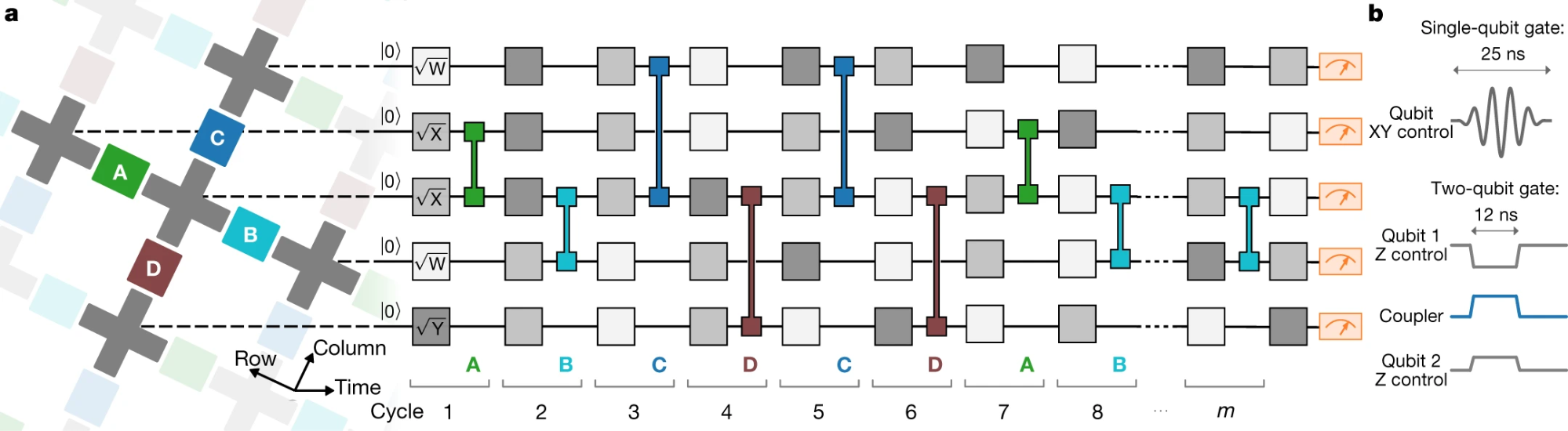
:
Google 53- , .
— Google , , , , , . , 2048- .
Resumen
( )

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
Conclusión
( )
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
( )

@Oxoron , “ ”
@a5b - “ ” , , .
, .
( )

[The National Academies Press]