Visualizar atractores extraños en Plotly es una obra maestra

La poesía es una sílaba muy hermosa, a menudo reflexiva, que no usamos en la vida cotidiana, pero nos encanta disfrutarla así. Lo mismo puede decirse de las matemáticas. En la película "Pi", el protagonista llama a las matemáticas "el lenguaje de la naturaleza", y en la película "Juegos de la mente", el protagonista habla de ella como un "tipo especial de arte". En la vida cotidiana, podemos olvidarlo por completo.

La aparición de atractores extraños es inusual y atractiva incluso en la dimensión bidimensional. Plotly le permite construirlos en tres dimensiones, y hace que sea muy fácil obtener un modelo 3D que pueda "girar" y a través del cual pueda "volar", una sensación de "tacto".

Como empezó todo

Todo comenzó hace mucho tiempo, en algún lugar de 2007 en la universidad conocí la teoría de la autoorganización y por primera vez vi el atractor de Lorenz, su ilustración en blanco y negro en un libro. Entonces me pareció demasiado extraño que algo pudiera moverse a lo largo de una trayectoria tan inusual. Incluso más extraño para mí parecía la idea misma de que casi todo en el mundo podría describirse con una sola teoría.

En general, todo es como siempre: mi visión del mundo ha cambiado, la vida continuó, el tiempo pasó. Y ahora, más recientemente, me encuentro con un enlace y veo esto:


Imagen tomada de chaoticatmospheres.com

"Hermosa", pensé. La idea de que todo esto se puede construir en Matplotlib también brilló, pero ya sabía de antemano que nada espectacular funcionaría. Y hace poco, hace solo dos semanas, conocí a Plotly e inmediatamente me di cuenta de que algo podía salir de eso.

El primer intento de construir inmediatamente falló. Resultó que las fórmulas en algunas imágenes de la "Galería de atractores extraños" contienen errores. Sin embargo, el autor de la galería honestamente advierte que no es matemático, como el autor de este artículo.

Un breve "google" hizo posible encontrar este código , que resultó ser extremadamente útil, y fue creado por Michael Tyka. Esta maravillosa persona creó un complemento completo para Blender, permitiéndole construir modelos (!) De 60 atractores. De hecho, pueden imprimirse en una impresora 3D, y dado que existen tecnologías de impresión de cera, es bastante fácil obtener un molde para fundir en bronce.

Código de visualización

Bueno, además de ser un matemático aficionado, también soy un programador aficionado. Por lo tanto, no juzgue estrictamente la calidad del código.

################################ ###   ### ################################ import numpy as np from scipy.integrate import odeint import plotly.graph_objects as go ################################## ###    ### ################################## #  : def LorenzMod1(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y*y - z*z + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.1 beta = 4 xi = 14 delta = 0.08 x_0, y_0, z_0 = 0, 1, 0 #      #  : tmax, n = 100, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod1, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) X, Y, Z = fT ####################### ###  ### ####################### # ,    : c = np.linspace(0, 1, n) #    : DATA = go.Scatter3d(x=X, y=Y, z=Z, line=dict(color= c, width=3, #   : # Greys,YlGnBu,Greens,YlOrRd,Bluered,RdBu, # Reds,Blues,Picnic,Rainbow,Portland,Jet, # Hot,Blackbody,Earth,Electric,Viridis,Cividis. colorscale="Cividis"), #   : mode='lines') fig = go.Figure(data=DATA) #   : fig.update_layout(width=1000, height=1000, margin=dict(r=10, l=10, b=10, t=10), #   : paper_bgcolor='rgb(0,0,0)', scene=dict(camera=dict(up=dict(x=0, y=0, z=1), eye=dict(x=0, y=1, z=1)), #   #     : aspectratio = dict(x=1, y=1, z=1), # ,    "aspectratio" aspectmode = 'manual', #  : xaxis=dict(visible=False), yaxis=dict(visible=False), zaxis=dict(visible=False) ) ) ###################### #!!  !!# ###################### fig.show() 

Como resultado, debería aparecer un modelo 3D de un atractor extraño llamado Lorenz Mod 1 :


Cabe señalar de inmediato que para resolver sistemas de ecuaciones diferenciales, la función odeint se seleccionó del módulo SciPy, que me pareció la forma más fácil y rápida de crear código de trabajo. Sin embargo, todas las ecuaciones pueden resolverse mediante el método habitual de Euler.

Para indicar los coeficientes en el código, por costumbre, utilicé los nombres de las letras griegas adoptadas en LaTeX. Cuando se trabaja con computadoras portátiles Jupyter, esto a veces es muy útil, ya que las fórmulas pueden convertirse rápidamente en código, y el código puede convertirse rápidamente en fórmulas.

Si es nuevo en el ecosistema de Python, pero desea que se garantice la ejecución del código, es mejor instalar la última versión de la distribución Python Anaconda , y el paquete Plotly a través de conda es el administrador de paquetes de distribución incorporado.

Dada la gran cantidad de atractores extraños, parece imposible construirlos a todos. Por lo tanto, en este artículo daré solo los más interesantes de los que logré construir.

El atractor Chen-Lee

 #  : def ChenLee(XYZ, t, alpha, beta, delta): x, y, z = XYZ x_dt = alpha*x - y*z y_dt = beta*y + x*z z_dt = delta*z + x*y/3 return x_dt, y_dt, z_dt #     : alpha = 5 beta = -10 delta = -0.38 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 200, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChenLee, (x_0, y_0, z_0), t, args=(alpha, beta, delta)) 

El atractor chua

 #  : def ChuaAttractor(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ h = zeta*x + (0.5*(delta - zeta))*(np.abs(x + 1) - np.abs(x - 1)) x_dt = alpha*(-x + y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 15.6 beta = 25.58 zeta = -5/7 delta = -8/7 x_0, y_0, z_0 = 1.8, -0.7, -2.85 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

El atractor Coullet

 #  : def Coullet(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ x_dt = y y_dt = z z_dt = alpha*x + beta*y + zeta*z + delta*x**3 return x_dt, y_dt, z_dt #     : alpha = 0.8 beta = -1.1 zeta = -0.4 delta = -1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 200, 20000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Coullet, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

El atractor de Dadras

 #  : def DadrasAttractor(XYZ, t, rho, sigma, tau, zeta, epsilon): x, y, z = XYZ x_dt = y - rho*x + sigma*y*z y_dt = tau*y - x*z + z z_dt = zeta*x*y - epsilon*z return x_dt, y_dt, z_dt #     : rho = 3 sigma = 2.7 tau = 1.7 zeta = 2 epsilon = 9 x_0, y_0, z_0 = 0.1, 0.03, 0 #      #  : tmax, n = 220, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DadrasAttractor, (x_0, y_0, z_0), t, args=(rho, sigma, tau, zeta, epsilon)) 

El atractor de Dequan Li

 #  : def DequanLi(XYZ, t, alpha, beta, delta, epsilon, rho, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = rho*x + xi*y -x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 1.833 delta = 0.16 epsilon = 0.65 rho = 55 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 50, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DequanLi, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, rho, xi)) 

El atractor de finanzas

 #  : def FinanceAttractor(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = (1/beta - alpha)*x + x*y + z y_dt = -beta*y - x**2 z_dt = -x - zeta*z return x_dt, y_dt, z_dt #     : alpha = 0.001 beta = 0.2 zeta = 1.1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 300, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FinanceAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

El atractor de cuatro alas

 #  : def FourWing(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = alpha*x + y + y*z y_dt = -x*z + y*z z_dt = -z - zeta*x*y + beta return x_dt, y_dt, z_dt #     : alpha = 5 beta = 16 zeta = 2 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 60000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FourWing, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

El atractor de Hadley

 #  : def HadleyAttractor(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -y*y - z*z - alpha*x + alpha*xi y_dt = x*y - beta*x*z - y + delta z_dt = beta*x*y + x*zz return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 4 xi = 8 delta = 1 x_0, y_0, z_0 = 0.39, -1, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HadleyAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

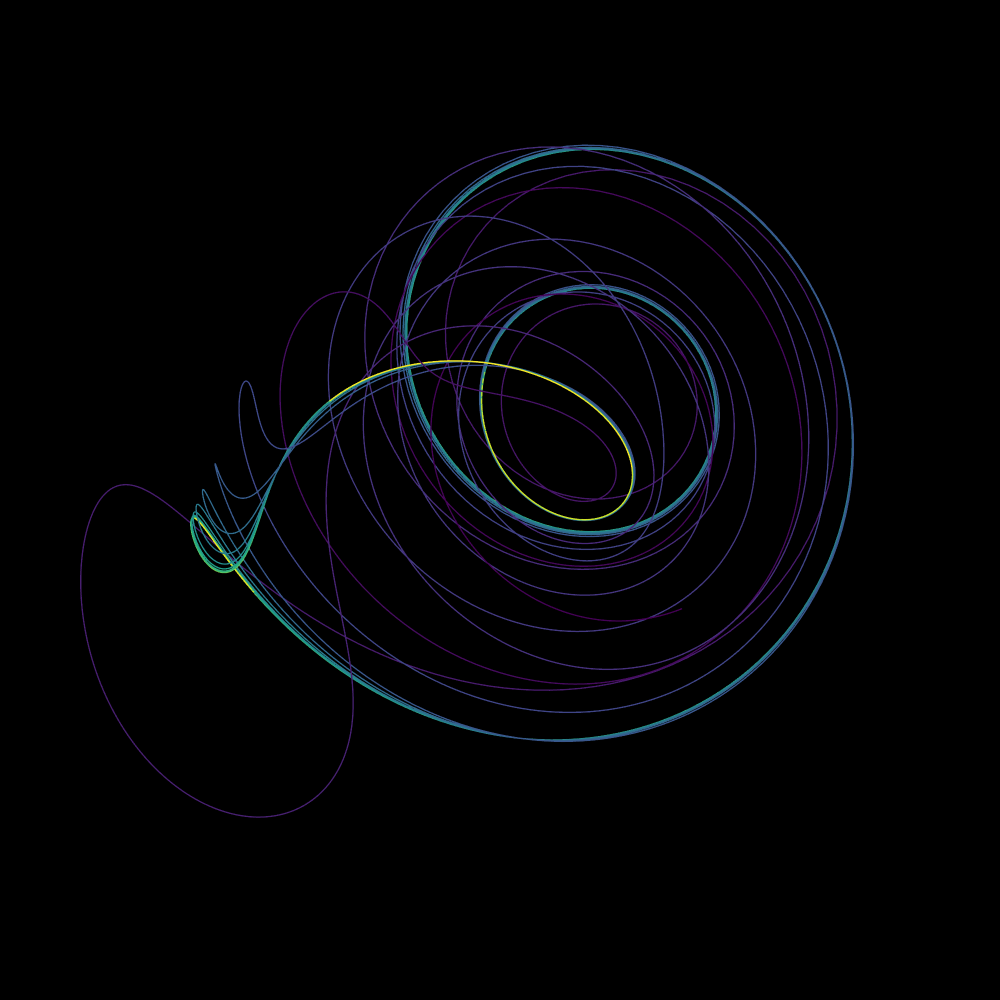
El atractor de Halvorsen

 #  : def HalvorsenAttractor(XYZ, t, alpha): x, y, z = XYZ x_dt = -alpha*x - 4*y - 4*z - y*y y_dt = -alpha*y - 4*z - 4*x - z*z z_dt = -alpha*z - 4*x - 4*y - x*x return x_dt, y_dt, z_dt #     : alpha = 1.4 x_0, y_0, z_0 = -5, 0, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HalvorsenAttractor, (x_0, y_0, z_0), t, args=(alpha,)) 

El atractor de Liu-Chen

 #  : def LiuChen(XYZ, t, alpha, beta, sigma, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*y + beta*x + sigma*y*z y_dt = delta*y - z + epsilon*x*z z_dt = xi*z - x*y return x_dt, y_dt, z_dt #     : alpha = 2.4 beta = -3.75 sigma = 14 delta = -11 epsilon = 4 xi = 5.58 x_0, y_0, z_0 = 1, 3, 5 #      #  : tmax, n = 55, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LiuChen, (x_0, y_0, z_0), t, args=(alpha, beta, sigma, delta, epsilon, xi)) 

El Atractor Lorenz Mod 2

 #  : def LorenzMod2(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y**2 -z**2 + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.9 beta = 5 xi = 9.9 delta = 1 x_0, y_0, z_0 = 5, 5, 5 #      #  : tmax, n = 50, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod2, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

El atractor caótico modificado de Chua

 #  : def ChuaModified(XYZ, t, alpha, beta, gamma, delta, zeta): x, y, z = XYZ h = -delta*np.sin((np.pi*x)/(2*gamma)) x_dt = alpha*(y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 10.82 beta = 14.286 gamma = 1.3 delta = 0.11 zeta = 7 x_0, y_0, z_0 = 1, 1, 0 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaModified, (x_0, y_0, z_0), t, args=(alpha, beta, gamma, delta, zeta)) 

El atractor de Newton Leipnik

 #  : def NewtonLeipnik(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -alpha*x + y + 10*y*z y_dt = -x - 0.4*y + 5*x*z z_dt = beta*z - 5*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.175 x_0, y_0, z_0 = 0.349, 0, -0.16 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NewtonLeipnik, (x_0, y_0, z_0), t, args=(alpha, beta)) 

El atractor nariz-aspiradora

 #  : def NoseHoover(XYZ, t, alpha): x, y, z = XYZ x_dt = y y_dt = -x + y*z z_dt = alpha - y*y return x_dt, y_dt, z_dt #     : alpha = 1.5 x_0, y_0, z_0 = 1, 0, 0 #      #  : tmax, n = 150, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NoseHoover, (x_0, y_0, z_0), t, args=(alpha,)) 

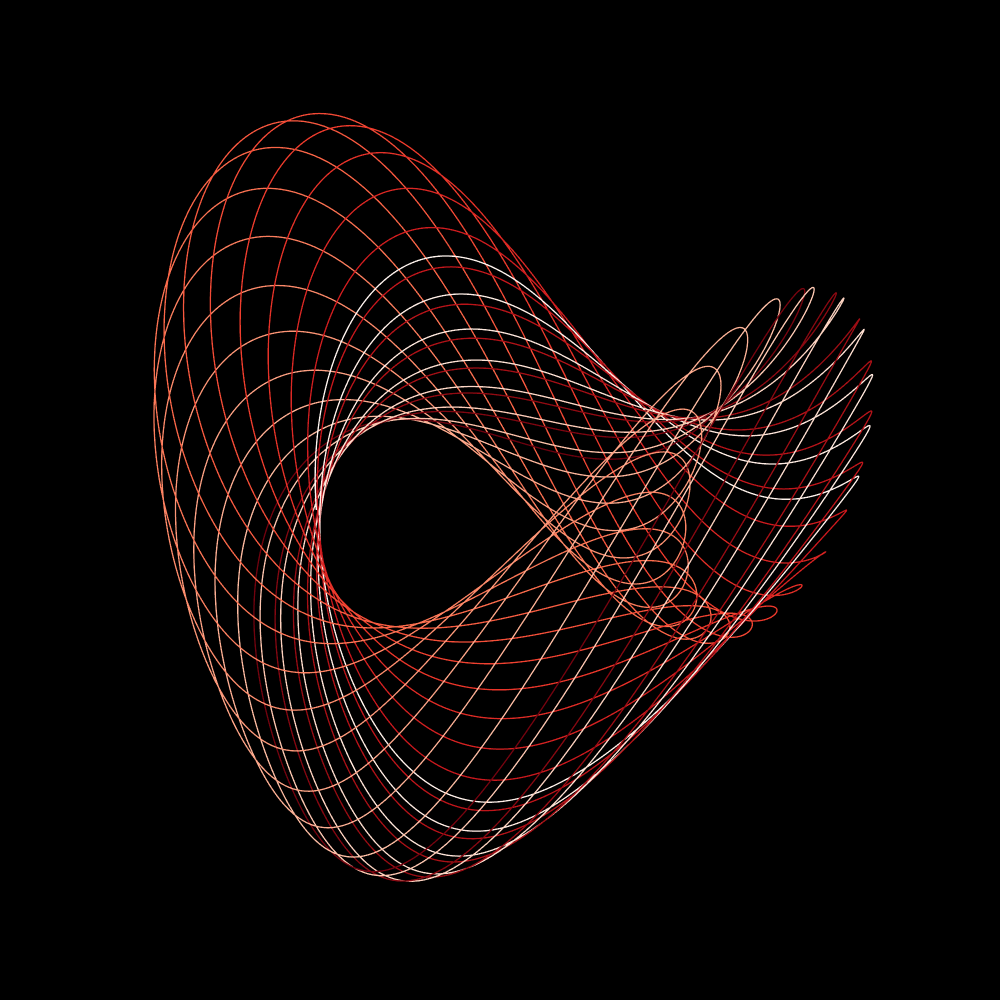
El atractor de Roessler

 #  : def Roessler(XYZ, t, alpha, beta, sigma): x, y, z = XYZ x_dt = -(y + z) y_dt = x + alpha*y z_dt = beta + z*(x - sigma) return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 0.2 sigma = 5.7 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Roessler, (x_0, y_0, z_0), t, args=(alpha, beta, sigma)) 

El atractor de Sakarya

 #  : def SakaryaAttractor(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -x + y + y*z y_dt = -x - y + alpha*x*z z_dt = z - beta*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.3 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(SakaryaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta)) 

El atractor de Thomas

 #  : def Thomas(XYZ, t, beta): x, y, z = XYZ x_dt = -beta*x + np.sin(y) y_dt = -beta*y + np.sin(z) z_dt = -beta*z + np.sin(x) return x_dt, y_dt, z_dt #     : beta = 0.19 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 185, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Thomas, (x_0, y_0, z_0), t, args=(beta,)) 

El atractor del sistema caótico unificado de tres volutas (TSUCS1)

 #  : def TSUCS1(XYZ, t, alpha, beta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = xi*y - x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 0.833 delta = 0.5 epsilon = 0.65 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 70, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(TSUCS1, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, xi)) 

El atractor wang-sun

 #  : def WangSunAttractor(XYZ, t, alpha, beta, zeta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*x + zeta*y*z y_dt = beta*x + delta*y - x*z z_dt = epsilon*z + xi*x*y return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = -0.01 zeta = 1 delta = -0.4 epsilon = -1 xi = -1 x_0, y_0, z_0 = 0.5, 0.1, 0.1 #      #  : tmax, n = 500, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(WangSunAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta, epsilon, xi)) 

En conclusión

Fuego, agua, tierra, cielo, sol, luna, estrellas: todas estas son las esencias poéticas más antiguas. Muy a menudo logro encontrar algo igualmente bello en matemáticas. Pero mucho más a menudo ni siquiera entiendo cómo hablar de todo esto en lenguaje matemático y lenguaje ordinario. No entiendo, pero quiero aprender.

Pero me di cuenta al 100% de que las herramientas de visualización modernas brindan una oportunidad fantástica para expresar su actitud hacia lo que está haciendo ahora, la oportunidad de mostrar lo importante que es para usted y lo interesante que es. Hazlo todo sin palabras.