La paradoja de Einstein - Podolsky - Rosen en los dedos y ... ¿qué tiene que ver el éter con él?

La paradoja de Einstein - Podolsky - Rosen ahora se estudia activamente en muchos laboratorios del mundo e institutos científicos. Se están escribiendo toneladas de artículos científicos. Se ha generado mucha publicidad en círculos casi científicos.


Solo un inconveniente, aunque bastante paradójico. En la mecánica cuántica en sí, ¡no hay nada paradójico en la paradoja EPR! No es un gramo!

Entonces, ¿por qué se está estudiando tan de cerca?

Y sí, ¿qué tiene que ver el éter con él?

Busca nueva física

La respuesta es simple: cuando se estudia la paradoja de EPR, hay una búsqueda activa de nueva física. Para ser precisos, la búsqueda de una nueva física fundamental, a medida que avanza el desarrollo de la física aplicada.

¡Esto es especialmente cierto en nuestro mundo, donde las bolas están regidas por teorías de conspiración que insinúan que los reptiles o los judíos en algún lugar ocultan física REAL!

Antagonista hasta el final del siglo XIX, cuando muchos físicos creían que casi todo estaba abierto, solo quedaba por encontrar algunos toques.

Ahora, por el contrario, incluso los físicos conservadores piensan que la física fundamental está lejos de ser completa.

¡Naturalmente, el interés en encontrar nueva física ahora es colosal!

Queda una cosa por entender: ¿cómo determinar dónde buscar esta veta dorada de la nueva física?
Una opción es encontrar inconsistencias en las teorías e intentar cavar allí.

Tomemos, por ejemplo, la teoría de la electrodinámica de Maxwell. Esta teoría es tan consistente con todas las teorías aceptadas que no hay nada que buscar. Y no mires. Bueno, excepto por las teorías unificadoras. Por la tarde con fuego no encontrarás nuevos artículos sobre electrodinámica fundamental. Aunque aplicado, un montón.

Coordinación de STO y GO

Sin embargo, la electrodinámica es difícil de mostrar bien en los dedos, así que tomemos algo más simple.
Veamos qué tan bien la teoría especial de la relatividad concuerda con la mecánica clásica (principalmente con la relatividad de Galileo).

La relatividad de Galileo en particular habla de la relatividad de la velocidad.

Y la teoría especial de la relatividad en particular afirma que la velocidad de la luz es absoluta.
Parece que el conflicto es obvio. Pero nosotros (en la persona de Einstein) declaramos a STR como una teoría generalizada de GO, donde la relatividad de Galileo es solo un caso especial.

De hecho, si en las transformaciones de Lorentz dirigimos la velocidad de la luz al infinito $$ , entonces obtenemos la transformación de Galileo. O, en otras palabras, para velocidades mucho más bajas que la velocidad de la luz, las transformaciones de Galileo serán válidas.

Por lo tanto, no vale la pena buscar una nueva física en la unión de la mecánica clásica y especial. Y hay muy pocos artículos nuevos sobre este tema. Esto no significa que todo se haya desenterrado en la estación de servicio. Puede buscar uno nuevo, por ejemplo, en el campo de los taquiones (partículas con velocidades superiores a la luz), y sí, están buscando allí.

Coherencia de la mecánica cuántica y clásica.

Pero, ¿qué pasa con la consistencia de la mecánica cuántica y clásica?
La mecánica clásica afirma en particular que las partículas existen aquí y ahora.
Y la mecánica cuántica afirma que las partículas son ondas, untadas en el tiempo, el espacio e incluso para nosotros mismos.

Aquí, también, el conflicto es obvio. Pero también puede salir: declaramos que KM es una teoría generalizada de la mecánica clásica (newtoniana).

De hecho, si en las soluciones de las ecuaciones de Schrödinger, disparamos la constante de Planck (reducida) a cero $$ entonces obtenemos leyes newtonianas. Bueno ... casi.

O, en otras palabras, si trabajamos a distancias mucho mayores que la longitud de onda de De Broglie, podemos usar las ecuaciones newtonianas. Bueno ... casi.
De hecho, esto no es suficiente. Y lo que es más incomprensible: no sabemos qué más hay que cambiar en la mecánica cuántica, excepto por el colapso de la función de onda, de modo que obtenemos la Mecánica Newtoniana.



Una de las inconsistencias más llamativas y simples entre estas dos teorías es la paradoja del gato Schrodinger.

La paradoja de Schrödinger establece que si tomamos un solo átomo radiactivo y colocamos un detector de radiación al lado de él como detonador (ya sea veneno o bombas). Ese gato al lado de este dispositivo:

• De acuerdo con la mecánica clásica, estará O vivo o muerto de todos modos
• De acuerdo con la mecánica cuántica, si el gato con el dispositivo está en una caja impenetrable, entonces, vivo y muerto al mismo tiempo, y solo la publicación de información lo obligará a cambiar al modo OR / OR

Puede parecer que se ha encontrado la mina de oro de la nueva física, ir y cavar, pero no es tan simple.
El hecho es que la parte que contradice se encuentra en el campo de la paradoja mundial del canguro (de hecho, la complicada paradoja de la tetera de Russell).

Afirma que cuando cerramos los ojos y apagamos los electrodomésticos, todo a su alrededor se convierte en un canguro. Pero si encendemos los electrodomésticos o abrimos los ojos, todo se convierte en lo que vemos.
La paradoja es que estos mundos no pueden ser probados ni refutados en principio y generalmente son descartados por la navaja de afeitar de Occam.

Esto significa que, aunque hemos encontrado una discrepancia entre la mecánica cuántica y la newtoniana, no hay ningún lugar para investigar, no se puede hacer un solo experimento que haya probado o refutado una de las versiones.

Búsqueda de nueva física y éter.

De hecho, la edad de oro del éter ya se extinguió hace más de un siglo. Ether surgió como asistente de las explicaciones de los campos de luz, eléctricos y magnéticos. Pero la estrella del éter brilló más intensamente en la segunda mitad del siglo XIX, cuando Maxwell agregó las ecuaciones de Ampère y combinó las ecuaciones básicas de electricidad y magnetismo en un solo sistema, creando la teoría del electromagnetismo.
Al resolver estas ecuaciones diferenciales, en particular, resultó que hay ondas electromagnéticas y que estas ondas se mueven a una velocidad constante $$ donde $$ - magnético y $$ - constante dieléctrica de vacío. Un poco más tarde resultó que esta velocidad es muy similar a la velocidad de la luz que pronto se midió, de lo que se concluyó que la luz son las ondas electromagnéticas de Maxwell.

Sin embargo, la declaración en sí tenía dos inconvenientes:

• Cuando hablamos de olas, nos referimos al entorno en el que se propagan estas olas. Olas del mar - en el agua, sonido - en el aire. ¿Y en qué se propagan las ondas electromagnéticas?
• El movimiento de las olas con velocidad constante era claramente contrario a la relatividad de las velocidades de Galileo.

Y si la primera es una pregunta más filosófica, entonces en el segundo caso, algo no estaba bien.
O bien Galileo tenía razón (y el principio de la relatividad de la velocidad es demasiado obvio para una contradicción), o bien Maxwell tenía razón (aunque lo que es más intuitivamente más correcto: ¿una solución a la diferencia o un principio obvio?), O ambos tenían razón (es terriblemente difícil cambiar la diferencia). encaja bajo Galileo).



La teoría del éter luminífero eliminó toda tensión; en primer lugar, resultó que las ondas electromagnéticas se propagan en el éter, y la velocidad de la luz es constante en relación con el éter estacionario, pero el movimiento del éter en sí es muy relativo. Es decir, resultó que tanto Maxwell como Galileo tienen razón. Bueno ... teóricamente.

Es cierto que la práctica no se detuvo. Las mediciones cada vez más precisas no mostraron desviaciones de la velocidad de la luz, no se pudo detectar viento etéreo.

Lorentz se dio cuenta de que el éter se esconde y cambia el espacio y el tiempo de tal manera que parece que no hay viento del éter y la velocidad de la luz es constante.

Einstein en 1905 solo eliminó la esencia innecesaria y creó la Teoría Especial de la Relatividad sobre la base de las transformaciones de Lorentz. Entonces el éter perdió la mitad de las funciones.

Finalmente, el éter luminífero murió como innecesario un poco más tarde con el desarrollo de la mecánica cuántica, y fue el descubrimiento de la dualidad onda-partícula en 1924. La luz ya no necesita un mediador, las ondas e / m se propagan en el fotón mismo.

Búsqueda de nueva física en la no localidad.

Del mismo modo, estamos buscando una discrepancia entre la mecánica clásica y la mecánica cuántica, pero para poder confirmarla con experimentos e intentar encontrar una explicación.

Estos son experimentos con violación de la localidad. Los científicos están más que seguros de que el mundo es local (no hay interacción a largo plazo, las partículas se comunican entre sí utilizando asistentes como un fotón y otros bosones de calibre).

Por otro lado, algunos de los resultados de la mecánica cuántica son claramente no locales.

Efectos no locales de la luz polarizada.

No, no veremos algo complicado, como la paradoja de EPR. Para darnos cuenta, utilizaremos un experimento mucho más fácil, a saber, la no linealidad de los efectos de la polarización de la luz. Para hacer esto, no necesitamos herramientas o instituciones megacomplejas. Es suficiente ir a la tienda de equipos fotográficos y comprar 2 filtros polarizados linealmente. Y eso es todo.

Por experiencia, colocaremos ambos filtros paralelos entre sí e iluminaremos con una linterna. Si los filtros son ideales, entonces todo el haz de luz que ha pasado por el primer filtro pasará por el segundo sin pérdida. Si hay un apagón, entonces se tiene en cuenta por separado como un coeficiente constante.



Entonces, si la polarización del segundo filtro paralelo está en un ángulo relativo al primer filtro (o viceversa), entonces el coeficiente de transmisión final según la mecánica cuántica es

$$

Es decir, si el ángulo es cero, entonces pasa el 100% de la luz, si 90 °, la luz está completamente bloqueada, pasa el 0%. Si el ángulo es de 45 °, la mitad del haz pasa el 50%. Etc.



La práctica muestra (la ley de Malus descubierta a principios del siglo XIX) que concuerda muy bien con la teoría.

Y ahora lo más importante:

Si cada partícula toma decisiones individualmente sin comunicarse con nadie, entonces estas decisiones no pueden explicarse utilizando la localidad.

Si puede, ¡continúe, complete un artículo y obtenga su Nobel!

Lo que podemos explicar con la ayuda de la localidad es una dependencia lineal, de modo que a 0 ° pasa el 100%, a 45 ° pasa al 50% y a 90 ° pasa al 0%. Sin embargo, en cualquier OTRO ángulo, los valores no convergen.

Ahora habrá hombres sabios y dirán, dejen que los fotones sientan el ángulo de polarización y, de acuerdo con la fórmula, echen suertes. Taki tendrá que complicar los experimentos para una coincidencia más exacta: exactamente individualmente, exactamente sin comunicación ...

No localidad en la paradoja de Einstein-Podolsky-Rosen

La paradoja de EPR afirma que es posible medir simultáneamente las propiedades cuánticas al violar el principio de incertidumbre de Heisenberg, lo que significa que la mecánica cuántica está incompleta.

Bohm sugirió experimentos para verificar esta paradoja con la ayuda de fotones o electrones enredados.



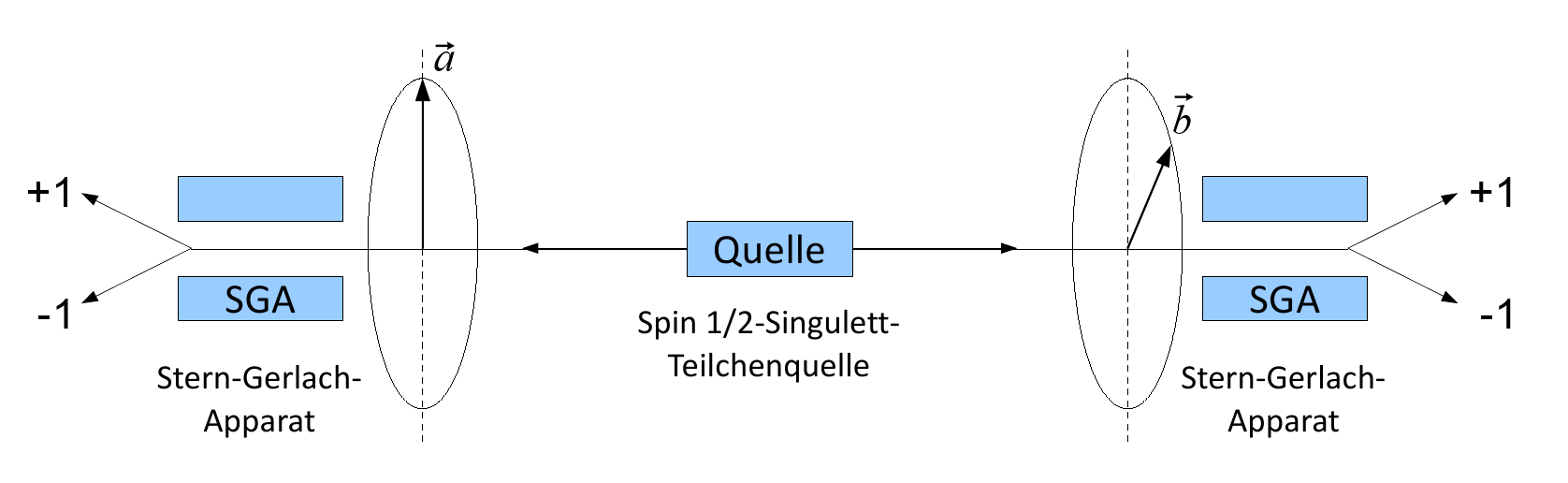
Imagine un experimento en el que 2 electrones se dispersan linealmente desde el centro y ambos pasan a través de 2 medidores de espín paralelos.

Para empezar, entenderemos lo que sucederá si los electrones son ordinarios, no enredados.

Todo es simple Los electrones giratorios pasarán por el primer medidor $$ en 50% de los casos y 50% de los casos $$ . A través del segundo, tanto.

Y si cambiamos los indicadores, ¿cuál será el resultado?
Obtendremos un promedio del 50% $$ y 50% de los casos con $$ . Trivial

Ahora complicaremos e intentemos encontrar las dependencias.

Háganos saber que una partícula con un giro pasó a través del primer metro $$ . Si no, ignore el resultado de pasar la segunda partícula. La pregunta es qué pasará por el segundo medidor en caso de que el primero sea $$ ? Obviamente, con una probabilidad del 50% mostrará el giro $$ y con una probabilidad del 50% $$ .

Por conveniencia, presentamos el índice de correlación, que es igual al módulo de la diferencia de probabilidad de ambas opciones:

$$

Nuestra correlación es cero.

El dispositivo tiene otro grado de libertad: los medidores de rotación se pueden girar independientemente uno del otro. ¿Y qué pasará si una partícula con un giro pasa a través del primer metro? $$ y el segundo medidor gira 90 ° con respecto al primero. Obviamente, un promedio del 50% $$ y 50% de los casos con $$ . Y nuevamente, la correlación es cero.

En general, donde quiera que vaya, no habrá correlación.



Pero, se vuelve mucho más interesante cuando enviamos electrones enredados.

Las partículas enredadas son muy simples: SIEMPRE tienen un giro hacia atrás uno con respecto al otro.

Si el primero tiene un giro $$ , entonces el segundo electrón enredado necesariamente tiene $$ girar

Y si el primero tiene un giro $$ entonces el segundo $$ .
Es decir, una correlación del 100%.

Pero, ¿qué sucede si giramos la segunda pinza 90 °? Si el primero tiene un giro $$ , entonces el segundo electrón enredado tendrá un promedio de 50% $$ y 50% de los casos con $$ . Resulta que la correlación es cero.

¿Qué sucede si giramos la segunda pinza 45 °? Si el primero tiene un giro $$ entonces el segundo electrón enredado tendrá un 25% de posibilidades $$ y 75% de probabilidad $$ . 50% de correlación.

En el caso general, de la teoría y la práctica, el nivel de correlación depende del ángulo mutuo de los medidores de espín:

$$

Es decir, de hecho, obtuvimos la misma ecuación no lineal que para el paso de fotones a través de filtros.

Puede intentar describir localmente la no linealidad utilizando parámetros ocultos, pero se violará la desigualdad de Bell para los parámetros aleatorios ocultos.

La teoría de Bell en la formulación de Clauser-Horn-Shimoni-Holt dice que para cuatro variables aleatorias la desigualdad siempre será cierta:

$$

donde K es la correlación sin módulo (y puede ser negativa).



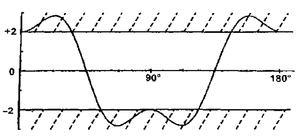
Solo para estos experimentos, se violará la desigualdad en algunos ángulos (cerca de 0 ° y 90 °), lo que significa que no pueden explicarse por parámetros ocultos aleatorios.

Conclusiones

Mientras que en la unión de la mecánica clásica y cuántica, la clásica pierde en seco. E incluso nos hace pensar que no sabemos algo sobre la localidad de la naturaleza, incluso si es local ...