El estudio de los neutrinos condujo a un descubrimiento inesperado en matemáticas.

Tres físicos querían calcular el proceso de cambio de neutrinos. Como resultado, encontraron una relación inesperada entre algunos de los objetos más comunes de las matemáticas.

Un día de agosto, la mañana después del desayuno, el matemático Terence Tao abrió un correo electrónico escrito por tres físicos con los que no estaba familiarizado. Trinity le explicó que se había topado con una fórmula simple que, de ser cierta, describiría una relación inesperada entre algunos de los objetos más básicos e importantes del álgebra lineal.

La fórmula "parecía demasiado buena para ser verdad", dijo Tao, profesor de la Universidad de California, Los Ángeles, ganador de Fields , uno de los matemáticos más importantes del mundo. "Algo tan breve y simple debería haber estado en los libros de texto hace mucho tiempo", dijo. "Por lo tanto, al principio pensé, no, esto no puede ser".

Y luego pensó un poco más.

Físicos - Stephen Park del Laboratorio Nacional de Aceleración. Fermi, Xining Zhang, de la Universidad de Chicago, y Peter Denton, del Laboratorio Nacional Brookhaven, obtuvieron esta identidad matemática dos meses antes, tratando de lidiar con el extraño comportamiento de las partículas elementales llamadas neutrinos .

Notaron que los " vectores propios ", difíciles de calcular, que describen en su caso cómo se propagan los neutrinos en la materia, se equiparan a una combinación de términos conocidos como "valores propios", que son mucho más fáciles de calcular. Además, se dieron cuenta de que esta relación entre los vectores propios y los valores propios, muy comunes en matemática, física y objetos de cálculo de ingeniería que se han estudiado desde el siglo XVIII, parece ser de un orden más general.

Aunque los físicos no podían creer que habían descubierto un hecho nuevo relacionado con matemáticas tan básicas, no podían encontrar esa relación ni en libros ni en artículos. Por lo tanto, decidieron arriesgarse y contactar a Tao, a pesar de que se hizo una solicitud en su sitio web para no molestarlo en tales casos.

"Para nuestra sorpresa, respondió dos horas más tarde y dijo que nunca había visto algo así antes", dijo Park. Y además de esto, en la respuesta de Tao había tres pruebas independientes de esta identidad.


Xining Zhang, Peter Denton y Stephen Park con su fórmula abierta

Una semana y media después, los físicos y Tao, a quienes Park llama la "manguera de bomberos de las matemáticas", publicaron un artículo en Internet informando una nueva fórmula. Ahora este trabajo es evaluado por especialistas de la revista Communications in Mathematical Physics. En un artículo separado publicado en el Journal of High Energy Physics, Denton, Park y Zhang usan esta fórmula para simplificar las ecuaciones que describen el comportamiento de los neutrinos.

Los expertos dicen que esta fórmula puede tener más formas de aplicar, porque en una gran cantidad de tareas, se requiere el cálculo de vectores propios y valores propios. "Tiene una amplia gama de usos", dijo John Bickom , especialista en física de partículas en la Universidad de Ohio. "Quién sabe qué puertas puede abrir".

Los matemáticos piensan de la misma manera. "Esto es sorprendente e interesante", dijo Van Wu , matemático de la Universidad de Yale. "No sospeché que fuera posible calcular vectores propios utilizando solo información sobre valores propios".

Vu y Tao demostraron una identidad similar en 2009 (es por eso que Denton, Park y Zhang decidieron contactar a Tao), pero la nueva fórmula obviamente no se sigue de la anterior. Y aunque una fórmula similar apareció por casualidad en un trabajo matemático en mayo de este año, sus autores no la asociaron con vectores propios y valores propios.

En cierto sentido, no es sorprendente que una nueva idea sobre objetos matemáticos de varios siglos de antigüedad provenga de físicos. La naturaleza ha inspirado la investigación matemática desde que la gente comenzó a contar con 10 dedos. "Para que las matemáticas prosperen, necesita estar conectado con la naturaleza", dijo Vu. "No hay otra manera".

Trucos de transformación

Los vectores propios y los valores propios son muy comunes porque caracterizan las transformaciones lineales: operaciones que estiran, comprimen, giran o de cualquier otra manera cambian todas las partes del mismo objeto por igual. Estas transformaciones están representadas por matrices rectangulares de números llamados matrices. Una matriz gira el objeto 90 grados; el otro lo voltea y lo parte por la mitad.


La aplicación de esta matriz a un objeto dado la reflejará en relación con el plano y también duplicará su altura. Los vectores propios de la matriz describen las direcciones en las que el objeto no cambia, a excepción de la escala. Los valores propios de la matriz describen cuánto escala el objeto a lo largo de estos vectores propios.
El vector propio A es paralelo al eje vertical. Su valor propio es 2, porque el objeto duplica su altura.
El vector propio B está en el plano de reflexión. Su valor propio es 1, porque el objeto no cambia a lo largo de él.
El vector propio C es perpendicular al plano de reflexión. Su valor propio es -1, lo que significa reflexión relativa al plano.
Al eliminar filas y columnas de una matriz, se pueden crear matrices más pequeñas. Sus valores propios junto con los valores propios de las matrices originales se pueden usar para calcular los vectores propios de las matrices originales.

Las matrices hacen esto cambiando los "vectores" de los objetos: flechas matemáticas que apuntan a cada lugar físico del objeto. Los vectores propios de una matriz son aquellos vectores que continúan apuntando en la misma dirección que antes, después de aplicar la matriz. Supongamos que tomamos una matriz que gira un objeto 90 grados alrededor del eje x: los vectores propios se dirigen a lo largo del eje x, ya que los puntos ubicados en este eje no giran cuando todos los demás giran a su alrededor.

Una matriz similar puede rotar objetos alrededor del eje x y comprimirlos dos veces. La matriz comprime o estira los vectores propios del objeto, según los valores propios correspondientes, en este caso, 1/2 (si el vector propio no cambia, su valor propio es 1).


Terence Tao

Los vectores propios y los valores propios son independientes y, por lo general, deben calcularse por separado, comenzando con las filas y columnas de la matriz misma. Los estudiantes aprenden a hacer esto para matrices simples. Pero la nueva fórmula es diferente de los métodos existentes. "Lo interesante de esta identidad es que no es necesario conocer ningún valor contenido en la matriz para calcular algo", dijo Tao.

La identidad se aplica a las matrices hermitianas que llevan a cabo transformaciones reales de vectores propios (en contraste con los números imaginarios) y, por lo tanto, se aplican a situaciones que ocurren en la realidad. La fórmula expresa cada vector propio de la matriz hermitiana en términos de los valores propios de esta matriz y su "matriz menor", una matriz tan pequeña, que se obtiene eliminando la fila y la columna del original.

Mirando hacia atrás, la fórmula parece razonable, dijo Tao, ya que los valores propios de la matriz menor codifican información oculta en sí mismos. Sin embargo, "por ejemplo, personalmente nunca hubiera pensado en tal cosa".

Dijo que una herramienta no relacionada con una tarea rara vez aparece en las matemáticas. Sin embargo, él cree que la interconexión de vectores propios y valores propios debe ser importante. "Es tan hermoso que estoy seguro de que la fórmula encontrará alguna aplicación en el futuro cercano", dijo. "Hasta ahora, solo tenemos un uso para ella".

Partículas de hombre lobo

Y esta aplicación está asociada con los neutrinos: la más extraña, menos estudiada y más secreta de las partículas fundamentales conocidas. Cada segundo, billones de tales partículas pasan a través del cuerpo humano, pero dado que prácticamente no muestran su presencia, muchas de sus propiedades siguen siendo desconocidas.

Curiosamente, la teoría afirma que son precisamente las diferencias en el comportamiento de los neutrinos y antineutrinos lo que puede hacer que la materia domine sobre la antimateria en el Universo . Si los dos opuestos aparecieran en cantidades iguales después del Big Bang, se aniquilarían entre sí y no quedaría nada en el espacio excepto la luz. La diferencia entre un neutrino y un antineutrino podría dar lugar a un exceso vital de materia. "Si se comportan de manera diferente, nos dará una idea de por qué el Universo está lleno de materia", dijo Deborah Harris , física de la Universidad de York y Fermilab, trabajando en el experimento DUNE (Deep Underground Neutrino Experiment, un neutrino subterráneo profundo). experimento) diseñado para medir tales diferencias.

El experimento, que medirá las características de los neutrinos lanzados desde Fermilab en Illinois a un detector subterráneo ubicado a 1300 km de la fuente en Dakota del Sur, utiliza el hecho de que hay tres tipos diferentes de neutrinos: electrón, muón y tau. Sin embargo, cada tipo es una mezcla de mecánica cuántica, y los neutrinos oscilan, cambiando sus tipos sobre la marcha. A medida que los neutrinos viajan desde Fermilab, su mezcla cambia, por lo que el neutrino muón puede convertirse en un electrón o tau neutrino.

Estas oscilaciones se describen mediante una matriz 3x3 extremadamente compleja. Con base en los vectores y valores propios, los físicos pueden calcular una expresión que describa la probabilidad de que un neutrino muón se convierta en un neutrino electrónico para cuando llegue a Dakota del Sur. También calculan la probabilidad de que un neutrino muón se convierta en un antineutrino electrónico.


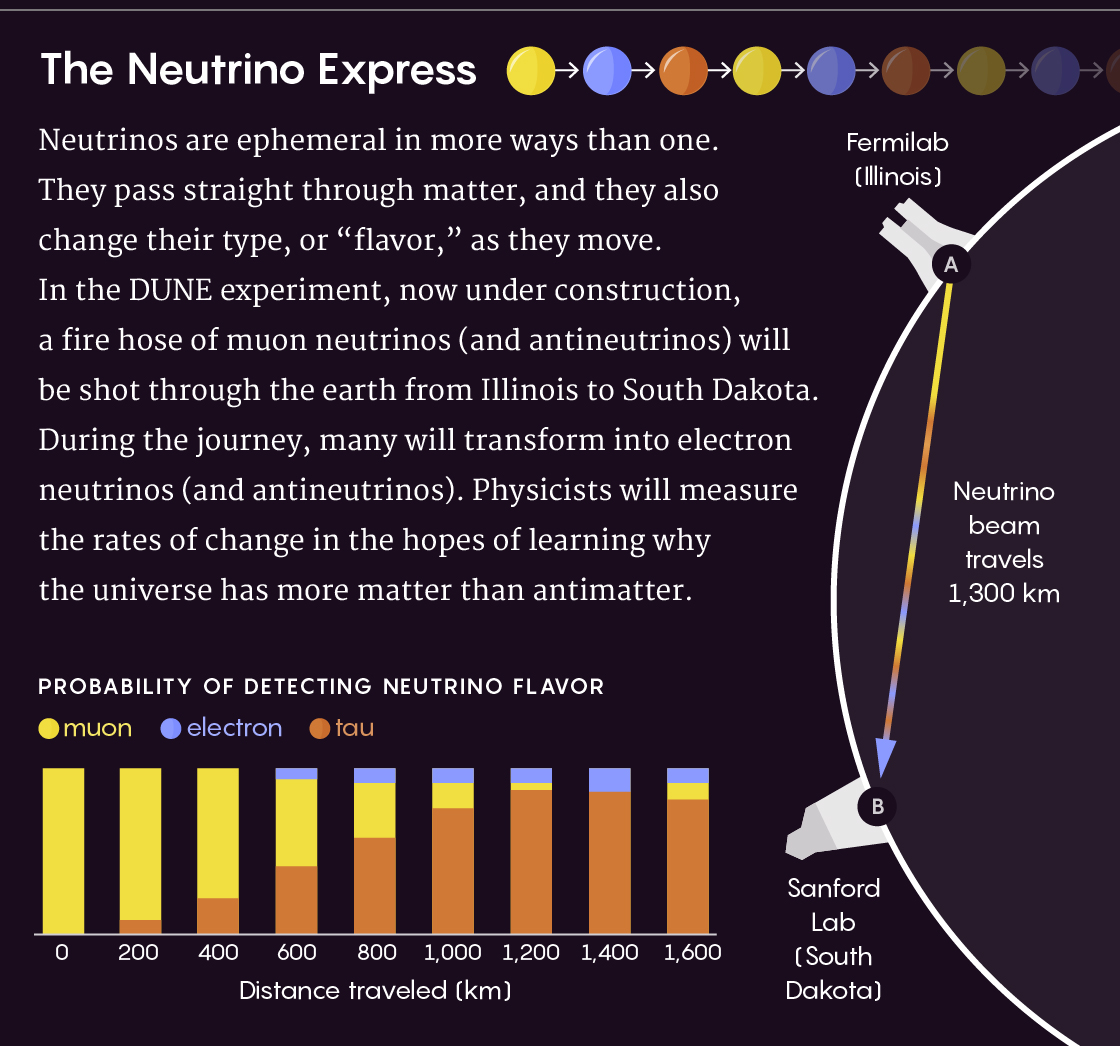Las partículas efímeras de un neutrino no solo atraviesan la materia, sino que también cambian su tipo sobre la marcha. En el experimento DUNE, se lanzará un haz de neutrinos, muchos de los cuales cambiarán sus tipos en el camino desde la fuente hasta el objetivo. Estos cambios serán medidos por los físicos.
El diagrama muestra la probabilidad de detectar neutrinos de varios tipos dependiendo de su distancia de viaje en km. Amarillo - muón, azul - electrónico, marrón - tau.

Estas expresiones contienen lo desconocido: la "fase de violación de la invariancia CP ", que muestra cómo las leyes de las oscilaciones de neutrinos y antineutrinos difieren entre sí. Al medir y comparar las relaciones de oscilación reales, los científicos con DUNE pueden calcular esto desconocido. Si la fase de perturbación es lo suficientemente grande, esto ayudará a explicar por qué el universo está lleno de materia.

Y como si estas dificultades no fueran suficientes, un efecto extraño, cuyos requisitos previos fueron descubiertos por primera vez en 1978 por el físico Lincoln Wolfenstein, hace que la matriz de neutrinos sea aún más compleja. Los neutrinos rara vez interactúan con la materia en el sentido habitual, pero Wolfenstein descubrió que su paso a través de la materia, a diferencia del espacio vacío, todavía cambia la forma en que se propagan. A veces, un neutrino que penetra a través de la materia interactúa con los electrones en un átomo, cambiando esencialmente de lugar con él: un neutrino electrónico se convierte en un electrón y viceversa.

Dichas sustituciones introducen un nuevo término en la matriz, que afecta a los neutrinos de electrones, lo que complica enormemente las matemáticas. Es este efecto de Mikheev - Smirnov - Wolfenstein [que fue predicho e investigado teóricamente por los físicos soviéticos Stanislav Mikheev y Alexey Smirnov en 1985 sobre la base del caso de oscilaciones de neutrinos en un medio con una densidad constante considerada en Wolfenstein] empujó a Park, Zhang y Denton a encontrar una manera de simplificar el cálculo .

La expresión para calcular los valores propios es más simple que la expresión para los vectores propios, por lo que Park, Zhang y Denton usaron esto como punto de partida. Antes de esto, desarrollaron un nuevo método para el cálculo aproximado de valores propios. En base a esto, notaron que las expresiones largas para vectores propios de trabajos anteriores eran iguales a combinaciones de estos valores propios. En conjunto, "puede calcular fácil y rápidamente las oscilaciones de neutrinos en la materia", dijo Zhang.

Con respecto a cómo vieron el patrón a partir del cual sigue la fórmula, los físicos no están completamente seguros. Park dice que simplemente notaron manifestaciones individuales del patrón y lo generalizaron. También admite que es bueno resolviendo acertijos. Es coautor de otra regularidad importante , descubierta en 1986, que facilitó los cálculos en el campo de la física de partículas, y que hasta el día de hoy inspira a los científicos a nuevos descubrimientos.

Y, sin embargo, el hecho de que el comportamiento extraño del neutrino podría conducir al surgimiento de nuevas ideas relacionadas con la matriz conmocionó a muchos. "La gente ha estado resolviendo el álgebra lineal durante mucho, mucho tiempo", dijo Park. "Todavía estoy esperando que alguien me envíe un correo electrónico donde diga: Si nos fijamos en este trabajo poco conocido de Cauchy , entonces hay esta fórmula en la nota del tercer apéndice".

Diferencia menor

De hecho, ya se conocía una fórmula similar, pero nadie la notó porque estaba enmascarada.

En septiembre, Tao recibió otro correo electrónico inesperado, esta vez de Jiyuan Zhang, un estudiante graduado en matemáticas de la Universidad de Melbourne en Australia. Zhang señaló la existencia de una fórmula equivalente en un trabajo que escribió con su curador Peter Forester en mayo, antes de que aparecieran el trabajo de Tao y tres físicos. Zhang y Forrester trabajaron en el campo de las matemáticas puras, la teoría de las matrices aleatorias. Aplicaron esta fórmula, explorando el problema asociado con la solución de Tao y sus colegas en 1999.

Forester nos explicó que, por primera vez, esta fórmula apareció en otra forma en el trabajo de 2001, escrito por Julia Baryshnikova , una matemática que ahora trabaja en la Universidad de Illinois en Urbana-Champaign, en cuyo trabajo se basaron Forester y Zhang. Pero estos matemáticos describieron los objetos de su identidad no como vectores propios, sino como términos necesarios para calcular los valores propios de ciertas matrices menores que aparecen en el curso de la resolución de su problema.

Forester llamó a la fórmula en su trabajo con Zhang "idéntica" a la utilizada por Tao y los tres físicos. Tao llamó a las fórmulas "casi idénticas", refiriéndose entre sí de la misma manera que los dos lados de la ilusión del conejo / pato. "Algunas personas buscaban conejos, otras solo buscaban patos", dijo.



Denton escribió en un correo electrónico que la fórmula que existía antes es "cercana a nuestro resultado, pero no perfecta". Agregó que "a la luz de la importancia de los vectores propios para muchos problemas, todavía creemos que nuestro resultado es bastante diferente del resto para considerarlo nuevo".

Quizás no sea tan extraño que en esta área en un solo verano después de varios siglos, pueda surgir una emoción tan repentina. "Hay muchos ejemplos de descubrimientos simultáneos en matemáticas", dijo Tao. - Los resultados de alguna manera cuelgan en el aire. Y la gente simplemente comienza a buscarlos en los lugares correctos ".