Una vez escribí
un artículo en el que describí un modelo matemático simple de la evolución de una red neuronal y su selección para la capacidad de agregar números en sistemas numéricos con bases 2 y una proporción áurea, y resultó que la proporción áurea funciona mejor. Entonces, mi primera experiencia resultó ser muy mala, ya que no tomé en cuenta una serie de matices importantes relacionados con el hecho de que el error no debería tenerse en cuenta para una neurona, sino para un poco de información, así que decidí mejorar mi experimento e introducir algunos más. ajustes
- Decidí verificar 100 pares de muestras de 15 (muestra de entrenamiento) y 1000 (muestra de prueba) vectores en sistemas numéricos con bases distribuidas uniformemente de 1.2 a 2 en lugar de dos bases conocidas previamente.
- También hice una regresión lineal no solo desde la distancia de la base a la proporción áurea, sino también desde la base misma, el número de coordenadas en el vector y el valor promedio de la coordenada en el vector de respuesta, para tener en cuenta la dependencia no lineal del error en la base.
- También verifiqué la normalidad de algunas muestras por el criterio de Kolmogorov-Smirnov, ANOV, pero estos criterios mostraron que las muestras probablemente se desvían del gaussiano, así que decidí hacer una regresión lineal ponderada en lugar de la habitual. Sin embargo, ANOVA, aunque mostró F un poco menos que antes (en la región de 700-800 en lugar de 800-900), pero el resultado siguió siendo más que estadísticamente significativo, lo que significa que se deben realizar más pruebas. Como estas pruebas, tomé un histograma de la densidad de distribución de los residuos de regresión y el QQ normal, un gráfico de la función de distribución de estos residuos.
Estos dos gráficos son:
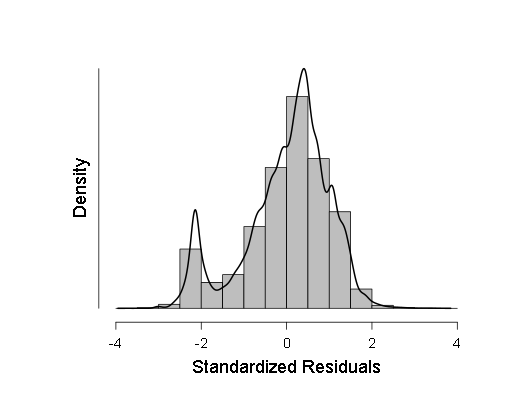
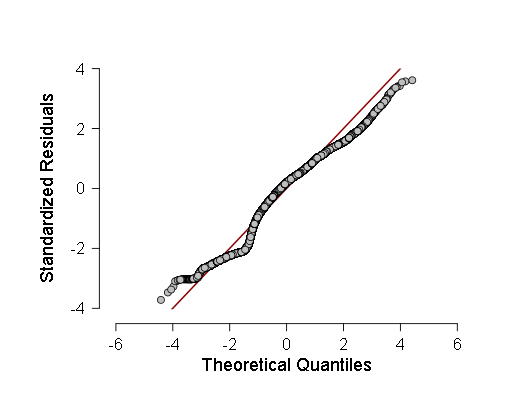
Como puede verse, aunque la desviación de la distribución normal en la distribución de los residuos es estadísticamente significativa (y a la izquierda, incluso un segundo modo pequeño es visible en el histograma), de hecho, está muy cerca del Gaussiano, por lo tanto, es posible (con precaución e intervalos de confianza más grandes) confiar en esta regresión lineal .
Ahora sobre cómo generé muestras para probar redes neuronales a través de ellas.
Aquí está el código para generar las muestras: Y aquí está el código del archivo de encabezado: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
También decidí publicar el código completo de la red neuronal: A continuación, hablemos sobre cómo realicé una regresión lineal ponderada. Para hacer esto, simplemente calculé las desviaciones estándar de los resultados de la red neuronal, y luego dividí la unidad en ellas.
Aquí está el código fuente del programa con el que hice esto: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
Luego, agregué los pesos resultantes a la tabla, donde reduje todos los datos obtenidos como resultado del programa, así como los valores de las variables para calcular la regresión, y luego los calculé en JASP. Aquí están los resultados:
Resultados
Regresión lineal
A continuación, tengo un histograma de la densidad de distribución de los residuos de regresión estandarizados:

Además del gráfico cuantil-cuantil normal de los residuos de regresión estandarizados:

Luego apliqué los valores promedio de los coeficientes de regresión obtenidos en su curso a las variables, y realicé mi análisis estadístico para encontrar el mínimo más probable de la función de error desde la base del sistema de números (cuánto está relacionado con estas variables) usando el lema de Fermat, el teorema de Bayes y el teorema de Lagrange. como sigue:
El hecho es que la distribución de las bases del sistema numérico en la muestra era obviamente uniforme, por lo tanto, si una determinada base en el intervalo (1,2; 2) es el mínimo del error cuadrático medio, entonces, según el lema de Fermat, tendrá una derivada cero, luego la densidad de probabilidad de los valores La función será infinita.
Ahora sobre cómo apliqué el teorema de Bayes. Calculé los intervalos de confianza de la distribución beta (esta es la distribución de probabilidad de "éxito" en el experimento bajo la condición de n "éxitos" ym "fracasos" con densidad de probabilidad
) los valores de la función de distribución (esta es la probabilidad de que la variable aleatoria no sea mayor que el argumento) de los errores calculados, basados en el hecho de que si la variable aleatoria no es mayor que el argumento, es "éxito", y si es más, entonces "fracaso". Luego, usando el teorema bayesiano, aplicamos la distribución beta de la función de distribución de los errores calculados y calculamos sus intervalos de confianza [función de distribución] del 99% en cada error calculado.
Pasamos al teorema de Lagrange. El teorema de Lagrange establece que si la función f (x) es continuamente diferenciable en el intervalo [a; b], entonces al menos en un punto de este intervalo tiene una derivada igual a
. Cómo aplico este teorema: el hecho es que la densidad de probabilidad es una derivada de la función de distribución, por lo que tomo el valor máximo entre los que toma exactamente en algunos intervalos desde el error mínimo hasta los errores restantes. Luego calculo los intervalos de confianza de tales valores en 98% (usando la corrección de Bonferroni) usando la siguiente fórmula:
donde F1 es el extremo izquierdo del intervalo de confianza para la función de distribución, y F2 es el derecho, x_i, x_1 son los errores calculados como argumento para la función de distribución. Luego, el programa busca un intervalo con el extremo izquierdo más grande y el extremo derecho más grande (de modo que el valor en el intervalo sea máximo), y luego busca el máximo y el mínimo en las bases que corresponden a los errores calculados en este intervalo. Estos máximos y mínimos son los argumentos de la función de error desde abajo, entre los cuales se encuentra el mínimo de la función en sí con una probabilidad del 98%.
Aquí está el código del programa que realicé este análisis estadístico con explicaciones: Y aquí está el código del archivo de encabezado: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
Aquí está el resultado del trabajo de este programa, cuando le di los fundamentos del sistema numérico y los resultados de la regresión:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
("(-" en este caso es solo una notación del signo "pertenece" de la teoría de conjuntos, y los corchetes indican el intervalo).
Por lo tanto, me resultó que la mejor base del sistema de números en términos de la menor cantidad de errores en la transmisión de información se encuentra en el rango de 1.501815 a 1.663988, es decir, la proporción áurea cae completamente en él. Es cierto, hice una suposición al calcular el mínimo y una más al calcular la cantidad de información en diferentes sistemas de números: en primer lugar, supuse que la función de error de la base es continuamente diferenciable y, en segundo lugar, que la probabilidad de que el número distribuido uniformemente sea de 1, 2 a 2 tendrán el número uno en un dígito específico, será aproximadamente el mismo después de algún dígito después del punto decimal.
Si hice algo completamente incorrecto, o simplemente incorrecto, estoy abierto a críticas y sugerencias. Espero que este intento haya sido más exitoso.
UPD Edité el artículo dos veces para aclarar algunos lugares en la parte "puramente científica", y también formateé el código.
UPD2. Después de consultar con una persona que entiende la bioinformática (un graduado del estudio de posgrado FBB MSU en IPPI RAS), se decidió reemplazar la palabra 《cerebro》 con network red neuronal》, ya que difieren mucho.