Reconocimiento de circuitos digitales. Elemento C generalizado

Alexander Kushnerov
18/12/2019

Incluso un ingeniero experimentado a veces puede tener dificultades para enrutar el circuito de modo que las pistas (o cables) no interfieran con su correcto funcionamiento. En una primera aproximación, el diseño y el número de nodos, qué cables están conectados a cada nodo y la longitud de los cables después de la ramificación, afectan la calidad del cableado. Si consideramos la longitud del cable como un retraso, entonces el funcionamiento correcto de los circuitos digitales asíncronos puede no depender de los retrasos en algunos cables. En el futuro, llamaremos seguros a dichos cables y la ramificación de dichos cables, completamente seguro (FGP). En este artículo, mostraremos cómo un circuito universal de doce transistores puede hacer que algunas ramas sean completamente seguras.

Considere el llamado esquema de "mariposa" [1], [2] que se muestra en la Fig. 1. Este circuito genera pulsos disjuntos p y q, que pueden usarse para controlar los transistores de potencia. Tampones en la Fig. 1 indica cables seguros. Se supone que el retraso de todos los demás cables es cero. La pausa entre pulsos se establece por los retrasos de los buffers wy y wz. En el futuro, no usaremos el búfer para indicar el retraso de un elemento. Los cables y las ramas en todos los circuitos de este artículo fueron probados para seguridad (persistencia de salida) en Workcraft [3]. Los gráficos de transición de señal (STG) se obtuvieron de los circuitos resolviendo conflictos CSC. Las ilustraciones muestran STG simplificados donde se eliminan las señales de búfer. Diagrama de tiempos (TD) en la Fig. 1 se construye de acuerdo con el STG correspondiente.


Fig. 1. El circuito "mariposa", su STG y TD bajo el supuesto de que los retrasos en los cables son cero.

Por la teoría [1], [2] se sabe que el circuito del disparador RS es sensible a los retrasos en los cables en el acoplamiento cruzado. Es por eso que los tampones en los enlaces cruzados en la Fig. 1 desaparecido Por lo tanto, los dos elementos de activación deben estar a una distancia mínima entre sí. Si esto es difícil de hacer, entonces dos elementos pueden ser reemplazados por un elemento complejo con retroalimentación. Por ejemplo, los elementos x y xb en el circuito de mariposa se pueden reemplazar como se muestra en la Fig. 2. Además, obtenemos FGP a la salida de un elemento complejo.


Fig. 2. Una variante del circuito en la Fig. 1 y su STG bajo el supuesto de que los retrasos en los cables son cero.

La implementación de los esquemas de la Fig. 1 y la fig. 2 requiere 16 y 20 transistores respectivamente. Además, el diagrama de la Fig. 2 es más lento, ya que los inversores wb1, wb2 y el inversor dentro del elemento 2 OR-AND deben cambiar dos veces por ciclo. El rendimiento lento suele ser el precio de FGP. Sin embargo, hay excepciones a esta regla. Por ejemplo, en la Fig. 3 muestra un esquema de un disparador de conteo asíncrono (AST) [4] que tiene dos FGP.


Fig. 3. AST y su STG bajo el supuesto de que los retrasos en los cables son cero.

Las desventajas del circuito en la Fig. 3 son una gran cantidad de cables y el hecho de que la mayoría de ellos se cruzan. Esto puede complicar el diseño, especialmente si el número de capas con pistas es limitado o están ocupadas por otros compuestos. Por lo tanto, debe buscar algún compromiso entre la cantidad de cables, la cantidad de transistores y la cantidad de FGP. Un ejemplo de tal esquema de compromiso con un FGP es el AST que se muestra en la Fig. 4. Esta es una pequeña modificación del circuito de [5]. Tenga en cuenta que aquí, como en el diagrama de la Fig. 2, se utiliza una base mixta. Para implementar este AST sin un indicador (XOR en wi2, wi4 y g5), se necesitan 26 transistores. Esto es solo dos transistores más que el AST en la Fig. 3)


Fig. 4. Comprometer AST y su STG, cuando los retrasos en los cables son cero.

Tenga en cuenta que todos los elementos con retroalimentación en la Fig. 2 y la fig. 4 son casos especiales de un elemento C generalizado (gC). Se da como [6]: $$$y = S (x) + y \ overline {R} (x)$donde $$$S (x)$y $$$R (x)$¿Las funciones de instalación y restablecimiento satisfacen la condición? $$$S (x) R (x) = 0$. Los casos especiales del elemento gC también son elementos NCL, que se utilizan en esquemas para el procesamiento de datos. Tenga en cuenta que el elemento NCL más grande tiene cuatro entradas y se implementa en 28 transistores [7]. Esto puede explicarse por el hecho de que con un mayor número de transistores, los cables se vuelven relativamente largos y la demora en ellos comienza a afectar el funcionamiento del elemento.

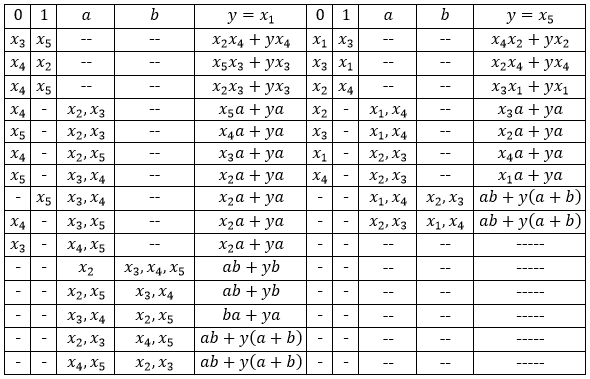
Considere el circuito del transistor que se muestra en la Fig. 5. Implementa la función de cinco variables [8], [9] $$$f (x) = x_1 x_3 + x_2 x_4 + x_5 (x_1 x_4 + x_2 x_3)$. La Tabla 1 muestra las funciones SDNF y SKNF $$$f (x)$y su doble función $$$φ (x) = \ overline {f (\ overline x)}$. De esta tabla es obvio que intercambiando $$$x_2$y $$$x_3$en $$$f (x)$tenemos $$$φ (x)$y viceversa. En caso $$$x_2 = x_3 = y$, obtenemos una función auto dual $$$f (x, y) = \ overline {f (\ overline x, \ overline y)} = x_1 x_4 x_5 + y (x_1 + x_4 + x_5)$.


Fig. 5. Un esquema que implementa la función de cinco variables.

Tabla 1. Formas de funciones lógicas para el circuito en la Fig. 5)


Tenga en cuenta que $$$x_2 = x_3 = y$significa que los cuatro transistores correspondientes deben conmutarse al mismo tiempo. Incluso si los cables después de la ramificación y tienen el mismo retraso, esto no es suficiente, ya que el momento de conmutación del transistor está determinado por el voltaje en su puerta. Desde este punto de vista, el análisis del circuito en la Fig. 5 se hizo en [10]. Sin embargo, este análisis no está completo, ya que solo se consideró la implementación de un elemento C de dos entradas. Para hacer un análisis completo, primero debe encontrar todas las opciones para combinar entradas o, más formalmente, todas las funciones de un número menor de variables que se pueden obtener de $$$f (x)$. Dicha búsqueda se realizó en una forma algo simplificada, y sus resultados se muestran en el apéndice. La mayoría de las características se encuentran en varias variaciones. De ellos es necesario elegir aquellos que ofrecen esquemas libres de competencia [11]. Todas las funciones obtenidas, el número de variantes de cada una de ellas y el número de la tabla correspondiente en el apéndice se dan en la tabla 2. Los números con un asterisco indican funciones duales.

Tabla 2. Los elementos gC implementados por el circuito en la Fig. 5)


Las funciones 2 y 2 *, 5 y 5 *, 7 y 7 * son dobles y la función 4 se puede obtener de la función 4 * intercambiando a y c. Tenga en cuenta que además de la función 6 *, todas las demás funciones son umbral. Esto puede explicarse por el hecho de que $$$f (x)$es isotónico (unte positivo) y el hecho de que para cuatro o menos variables las funciones isotónicas coinciden con el pseudo-umbral [12]. La pregunta de qué opciones son para las funciones 1 *, 3 * y 6 * en este artículo permanece abierta.

Considere el caso de las funciones 2 y 2 * como ejemplo. De acuerdo con una de las opciones (tabla P3 en el apéndice) $$$x_1 = x_4 = a$y $$$x_2 = x_3 = b$. Deja salir $$$y$desconectado de la entrada $$$x_5$y deje que la señal se elimine de la entrada del inversor. Esto le permite construir un distribuidor de cinta transportadora [13] que se muestra en la Fig. 6. Los elementos en esta celda son diferentes, pero debido al hecho de que las entradas están combinadas, ambas implementan la misma función auto dual. Tenga en cuenta que los elementos reticulados en los circuitos de la Fig. 1, en la Fig. 3 y en la Fig. 6 son casos especiales de la construcción básica para una implementación perfecta [2]. Por lo tanto, debe haber reglas para transformar los circuitos de diseño básicos en circuitos de elementos gC y viceversa.


Fig. 6. Distribuidor de cinta transportadora.

Desde el punto de vista de la tecnología, los transistores deben ser "encadenados" en autobuses de polisilicio. Tal implementación del circuito en la Fig. 5 se da en [14]. Para establecer los estados iniciales, se pueden usar transistores p-MOS y n-MOS, que crean un divisor de voltaje con transistores en el inversor. La inmunidad al ruido de los circuitos se puede aumentar con la ayuda de ciertas transformaciones STG [15].

Agradecimientos

El autor agradece profundamente a Svetlana Frolova (OmSU) por escanear el artículo [1], y también a Sergey Bystrov por inspiración.

App

MuPAD se utilizó para obtener los resultados presentados en esta sección. Deje que la salida y se conecte solo a una de las entradas. La Tabla A1 muestra que en este caso $$$S (x) R (x) ≠ 0$. Para obtener funciones para las cuales $$$S (x) R (x) = 0$, puede combinar algunas variables o asignarles constantes. Las funciones para el caso de combinar dos variables se dan en la tabla A2. Otras opciones no dan $$$S (x) R (x) = 0$. Como las primeras cuatro funciones en la Tabla A1 coinciden con una permutación de las variables, consideraremos solo la primera y la quinta. Casos $$$y = y (∀)$y $$$y = (∀) + y$no es interesante, porque en el primero solo podemos restablecer el elemento gC, pero no podemos instalarlo, y en el segundo, viceversa. Las manipulaciones con las variables permitieron obtener de la tabla P1 las funciones de cuatro y tres variables, que se dan en la tabla P3 y la tabla P4, respectivamente.

Tabla A1. Funciones de cinco variables.


Tabla A2. Funciones de cuatro variables.


Tabla P3. Funciones de cuatro variables obtenidas de la Tabla A1.


Cuadro A4. Las funciones de las tres variables obtenidas de la Tabla A1.

Literatura

[1] V. I. Varshavsky, M. A. Kishinev, A. R. Taubin y B. S. Zirlin, “Análisis de circuitos lógicos asíncronos. II Accesibilidad de los estados operativos y el efecto de los retrasos en los cables ”, Izv. Academia de Ciencias de la URSS. Cibernética técnica, no. 4, pp. 84-97, 1982.
[2] Varshavsky, V. I. (ed.), Control automático de procesos asincrónicos en computadoras y sistemas discretos, Nauka, 1986.
[3] workcraft.org .
[4] RC Todd, "Sistema lógico". Patente US3609569, 28 de septiembre. 1971
[5] EA Vittoz, "Estructura lógica de división de frecuencia". Patente US3829714, 13 de agosto. 1974.
[6] J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno y A. Yakovlev, Síntesis lógica para controladores e interfaces asíncronos, Springer, 2002.
[7] A. Kondratyev, "Flujo asincrónico de riel múltiple con detección de terminación y sistema y método para diseñar el mismo". Patente US6526542, 25 de febrero. 2003.
[8] JJ Gibson, "Circuitos lógicos que emplean transistores de efecto de campo". Patente US3439185, 15 de abril. 1969
[9] R. Miller, Teoría de los circuitos de conmutación. Volumen I. Esquemas combinados, Ciencia, 1970.
[10] K. van Berkel, "Cuidado con la bifurcación isocrónica", Integración, vol. 13, no. 2, pp. 103-128, 1992.
[11] P. Kudva, G. Gopalakrishnan, H. Jacobson y SM Nowick, "Síntesis de redes CMOS de puertas complejas personalizadas sin riesgos bajo cambios de entrada múltiple", en Design Automation Conf., 1996.
[12] GW Fagerlin, Enumeración de funciones pseudo-separables de cinco variables. M.Sc. Tesis, Universidad de Illinois, 1968.
[13] V. I. Varshavsky, A. Yu. Kondratiev, N. M. Kravchenko y B. S. Tsirlin, "Distribuidor asincrónico". Patente SU1598142, 07/10 1990.
[14] SW Cheng, "Circuito lógico CMOS H-tree", en IEEE Conf. en Electrónica, Circuitos y Sistemas, 2008.
[15] A. Taubin, A. Kondratyev, J. Cortadella y L. Lavagno, "Transformaciones de comportamiento para aumentar la inmunidad al ruido en especificaciones asincrónicas", en IEEE Symp. en asíncrono. Circuitos y sistemas, 1999.