Escribimos una "calculadora" en C #. Parte I. Cálculo del valor, derivada, simplificación y otros gansos.

Hola

Por alguna razón, nuestra calculadora está asociada con algo que todo principiante debería escribir. Quizás porque históricamente las computadoras para ese propósito fueron creadas para contar. Pero escribiremos una calculadora difícil, no simulada, por supuesto, pero para poder realizar operaciones algebraicas básicas, como la diferenciación, la simplificación y características como la compilación para acelerar los cálculos.


Tomamos las galletas restantes del año nuevo, ¡y manejamos!

Conjunto de expresión

¿Qué es una expresión?

Por supuesto, esto no es una línea. Es bastante obvio que una fórmula matemática es un árbol o una pila, y aquí nos detenemos en el primero. Es decir, cada nodo, cada nodo de este árbol, es algún tipo de operación, variable o constante.



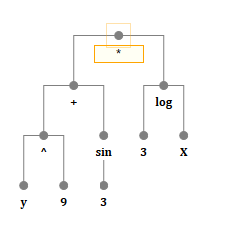
Una operación es una función o un operador, en principio, aproximadamente lo mismo. Sus hijos son los argumentos de una función (operador).

Jerarquía de clases en su código

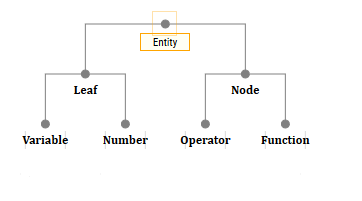
Por supuesto, la implementación puede ser cualquiera. Sin embargo, la idea es que si su árbol consta solo de nodos y hojas, entonces son diferentes. Por lo tanto, llamo a estas "cosas" - entidades. Por lo tanto, la clase superior será la clase abstracta Entidad.


Y también habrá cuatro clases sucesoras: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.

¿Cómo construir una expresión?

Primero, construiremos una expresión en el código, es decir

var x = new VariableEntity("x"); var expr = x * x + 3 * x + 12; 

Si declara una clase vacía VariableEntity, dicho código le arrojará un error, dicen que no sabe cómo multiplicar y sumar.

Operadores primordiales

Una característica muy importante y útil de la mayoría de los idiomas, que le permite personalizar la ejecución de operaciones aritméticas. Se implementa sintácticamente de manera diferente según el idioma. Por ejemplo, una implementación en C #

 public static YourClass operator +(YourClass a, YourClass b) { return new YourClass(a.ToString() + b.ToString()); } 

Obtenga más información sobre cómo anular declaraciones en C #
El nabo se implementa aquí .

Fundición (no) explícita

En lenguajes compilados como C #, tal cosa suele estar presente y le permite convertir el tipo si es necesario sin llamar adicionalmente a myvar.ToAnotherType (). Entonces, por ejemplo, sería conveniente escribir

 NumberEntity myvar = 3; 

En lugar de lo habitual

 NumberEntity myvar = new NumberEntity(3); 

Más información sobre la conversión de tipos en C #
El nabo se implementa en esta línea.

Colgando

La clase Entity tiene un campo Hijos; esta es solo una lista de Entity, que son los argumentos para esta entidad.


Cuando llamamos a una función u operador, debemos crear una nueva entidad y poner en ella los elementos secundarios desde los que se llama la función u operador. Por ejemplo, la cantidad en teoría debería verse así:

 public static Entity operator +(Entity a, Entity b){ var res = new OperatorEntity("+"); res.Children.Add(a); res.Children.Add(b); return res; } 

Es decir, ahora si tenemos la entidad xy la entidad 3, entonces x + 3 devolverá la esencia del operador de suma con dos hijos: 3 y x. Entonces, podemos construir árboles de expresión.

Una llamada de función es más simple y no tan bella como con un operador:

 public Entity Sin(Entity a) { var res = new FunctionEntity("sin"); res.Children.Add(a); return res; } 

Colgar en nabos se implementa aquí .

Ok, inventamos un árbol de expresión.

Sustitución variable

Aquí todo es extremadamente simple. Tenemos Entidad: verificamos si es una variable en sí misma; de ser así, devolvemos el valor; de lo contrario, ejecutamos los elementos secundarios.

Este enorme archivo de 48 líneas implementa una función tan compleja.

Cálculo del valor

En realidad, por lo que todo esto es. Aquí se supone que debemos agregar algún tipo de método a la entidad

 public Entity Eval() { if (IsLeaf) { return this; } else return MathFunctions.InvokeEval(Name, Children); } 

La hoja no ha cambiado, pero para todo lo demás tenemos un cálculo personalizado. Nuevamente, daré solo un ejemplo:

 public static Entity Eval(List<Entity> args) { MathFunctions.AssertArgs(args.Count, 1); var r = args[0].Eval(); if (r is NumberEntity) return new NumberEntity(Number.Sin((r as NumberEntity).Value)); else return r.Sin(); } 

Si el argumento es un número, entonces produciremos una función numérica, de lo contrario la devolveremos tal como estaba.

Número?

Esta es la unidad más simple, el número. Se pueden realizar operaciones aritméticas en él. Por defecto, es complejo. También tiene operaciones como Sin, Cos y algunas otras definidas.

Si está interesado, el número se describe aquí .

Derivada

Cualquiera puede calcular la derivada numéricamente, y dicha función se escribe verdaderamente en una línea:

 public double Derivative(Func<double, double> f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5; 

Pero, por supuesto, queremos una derivada analítica. Como ya tenemos un árbol de expresión, podemos reemplazar recursivamente cada nodo de acuerdo con la regla de diferenciación. Debería funcionar algo como esto:



Aquí, por ejemplo, cómo se implementa la cantidad en mi código:

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) + b.Derive(variable); } 

Pero el trabajo

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) * b + b.Derive(variable) * a; } 

Y aquí hay una solución en sí misma:

 public Entity Derive(VariableEntity x) { if (IsLeaf) { if (this is VariableEntity && this.Name == x.Name) return new NumberEntity(1); else return new NumberEntity(0); } else return MathFunctions.InvokeDerive(Name, Children, x); } 

Este es el método de la entidad. Y como vemos, la hoja tiene solo dos estados: o es una variable por la cual nos diferenciamos, luego su derivada es 1, o es una constante (número o Entidad Variable), luego su derivada es 0, o un nodo, luego hay una referencia por nombre (InvokeDerive se refiere al diccionario de funciones, donde se encuentra el deseado (por ejemplo, la suma o el seno)).

Tenga en cuenta que no dejo algo como dy / dx aquí y digo de inmediato que la derivada de la variable que no nos diferencia es 0. Pero aquí se hace de manera diferente.

Toda la diferenciación se describe en un archivo , pero no es necesario más.

Simplificación de la expresión. Patrones

La simplificación de la expresión generalmente no es trivial en principio. Bueno, por ejemplo, qué expresión es más simple: $$$x ^ 2 - y ^ 2$o $$$(x - y) (x + y)$? Pero nos adherimos a algunas ideas y, sobre la base de ellas, queremos hacer esas reglas que simplifiquen con precisión la expresión.

Es posible escribir en cada Eval que si tenemos la suma, y ​​los niños son trabajos, entonces clasificaremos cuatro opciones, y si algo es igual en alguna parte, eliminaremos el factor ... Pero, por supuesto, no quiero hacer eso. Por lo tanto, puede adivinar el sistema de reglas y patrones. Entonces, ¿qué queremos? Algo así como esta sintaxis:

 { any1 / (any2 / any3) -> any1 * any3 / any2 }, { const1 * var1 + const2 * var1 -> (const1 + const2) * var1 }, { any1 + any1 * any2 -> any1 * (Num(1) + any2) }, 

Aquí hay un ejemplo de un árbol en el que se encontró un subárbol (marcado en verde) que coincide con el patrón any1 + const1 * any1 (any1 encontrado está marcado en naranja).



Como puede ver, a veces es importante para nosotros que la misma entidad deba repetirse, por ejemplo, para acortar la expresión x + a * x, necesitamos que x esté allí y allí, porque x + a * y ya no se reduce. Por lo tanto, necesitamos hacer un algoritmo que no solo verifique que el árbol coincida con el patrón, sino que también

1. Verifique que el mismo patrón de entidad coincida con la misma entidad.
2. Escribir lo que corresponde a qué, luego sustituir.

El punto de entrada se parece a esto:

 internal Dictionary<int, Entity> EqFits(Entity tree) { var res = new Dictionary<int, Entity>(); if (!tree.PatternMakeMatch(this, res)) return null; else return res; } 

Y en tree.PaternMakeMatch, rellenamos recursivamente el diccionario con claves y sus valores. Aquí hay un ejemplo de una lista de Entidades de patrones:

 static readonly Pattern any1 = new Pattern(100, PatType.COMMON); static readonly Pattern any2 = new Pattern(101, PatType.COMMON); static readonly Pattern const1 = new Pattern(200, PatType.NUMBER); static readonly Pattern const2 = new Pattern(201, PatType.NUMBER); static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION); 

Cuando escribimos any1 * const1 - func1 y así sucesivamente, cada nodo tendrá un número, esta es la clave. En otras palabras, al completar el diccionario, estos números aparecerán como claves: 100, 101, 200, 201, 400 ... Y al construir un árbol, veremos el valor correspondiente a la clave y lo sustituiremos.

Implementado aquí .

Simplificacion Clasificación de árboles

En el artículo que ya he abordado, el autor decidió hacerlo de manera simple, y lo clasificó prácticamente por el hash del árbol. Se las arregló para reducir a y -a, b + c + b para convertir 2b + c. Pero, por supuesto, también queremos que se reduzca (x + y) + x * y - 3 * x, y en general cosas más complicadas.

¿Los patrones no funcionan?

En general, lo que hicimos antes, los patrones son una cosa monstruosamente maravillosa. Le permitirá reducir la diferencia entre los cuadrados y la suma del cuadrado del seno y el coseno, y otras cosas complejas. Pero la palma elemental, ((((((x + 1) + 1) + 1) + 1), no se reducirá, porque la regla principal aquí es la conmutatividad de los términos. Por lo tanto, el primer paso es aislar a los "hijos lineales".

"Niños lineales"

En realidad, para cada nodo de la suma o diferencia (y, por cierto, el producto / división), queremos obtener una lista de términos (factores).



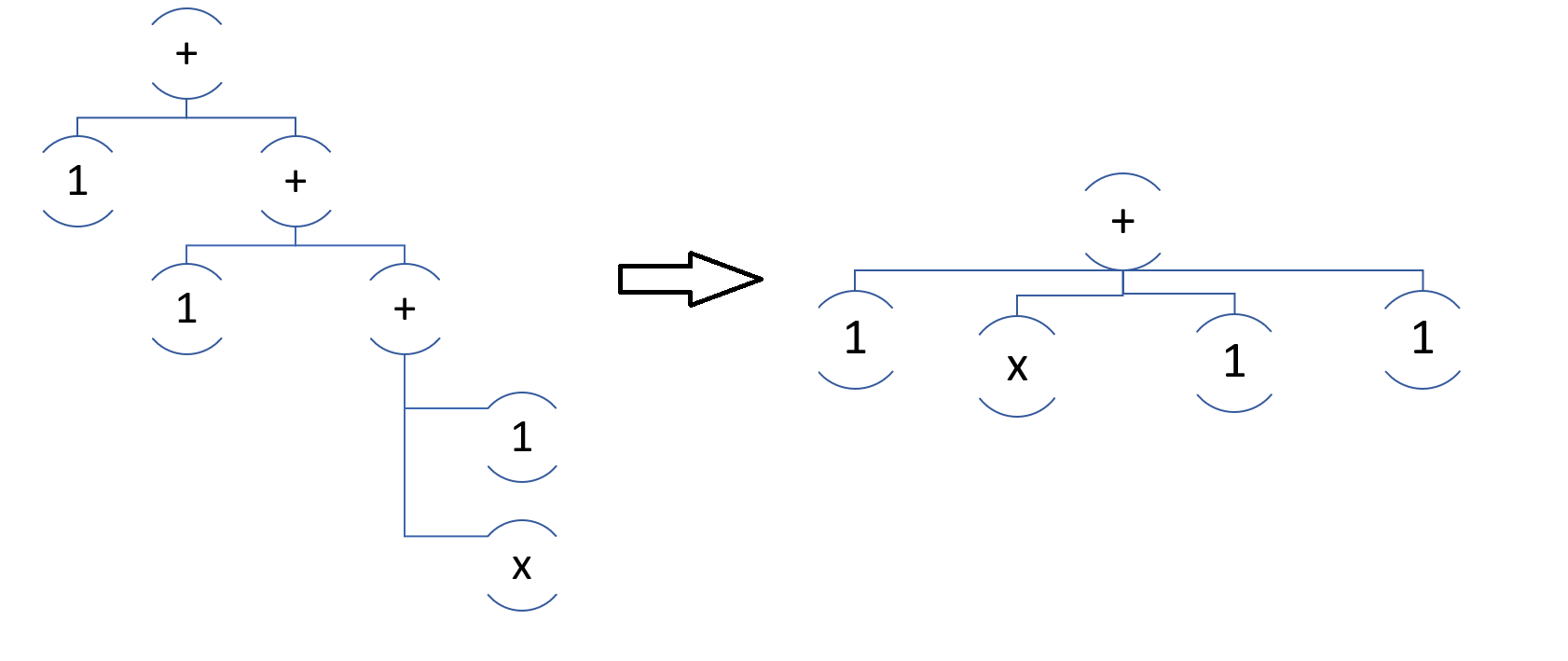
Esto es básicamente sencillo. Deje que la función LinearChildren (Entity node) devuelva una lista, luego miramos al niño en el nodo. Niños: si el niño no es una suma, entonces result.Add (child), de lo contrario result.AddRange (LinearChildren (child)).

No es la forma más bella implementada aquí .

Agrupando niños

Entonces tenemos una lista de niños, pero ¿qué sigue? Supongamos que tenemos sin (x) + x + y + sin (x) + 2 * x. Obviamente, nuestro algoritmo recibirá cinco términos. A continuación, queremos agrupar por similitud, por ejemplo, x parece 2 * x más que sin (x).

Aquí hay una buena agrupación:



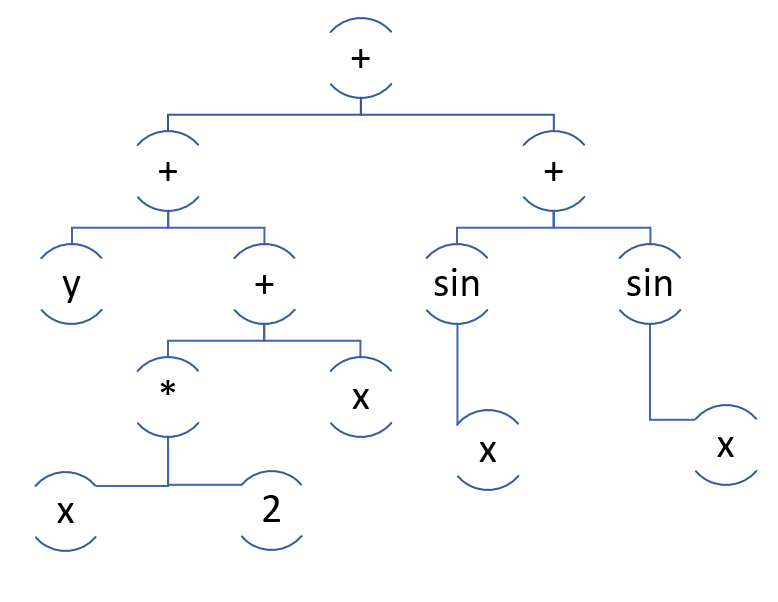
Dado que los patrones en él harán frente a la conversión de 2 * x + x a 3 * x.

Es decir, primero agrupamos por algún hash , y luego hacemos MultiHang - convirtiendo la sumatoria n-aria a binaria.

Hash de nodo

Por un lado $$$x$y $$$x + 1$debe colocarse en un grupo. Por otro lado, si está disponible $$$a * x$poner en un grupo con $$$y * (x + 1)$sin sentido


Por lo tanto, implementamos la ordenación multinivel. Primero, pretendemos que $$$x + 1$- Lo mismo. Ordenado, calmado. Entonces pretendemos que $$$x + 1$solo se puede colocar con otros $$$x + 1$. Y ahora nuestro $$$a * (x + 1)$y $$$y * (x + 1)$finalmente se unió. Implementado simplemente:

 internal string Hash(SortLevel level) { if (this is FunctionEntity) return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level)); else if (this is NumberEntity) return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " "; else if (this is VariableEntity) return "v_" + Name; else return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level)); } 

Como puede ver, la función afecta la clasificación de cualquier manera (por supuesto, porque $$$f (x)$con $$$x$generalmente no conectado en el caso general). Como una variable, $$$x$con $$$y$Bueno, no se va a mezclar. Pero las constantes y los operadores no se tienen en cuenta en todos los niveles. En este orden, el proceso de simplificación en sí mismo

 public Entity Simplify(int level) { //      :   ,   ,     . . var stage1 = this.InnerSimplify(); Entity res = stage1; for (int i = 0; i < level; i++) { //     .    -  x  x+1 (  ),  -  x-1  x+1 (,   ),  -  x+1  x+1 ( ). switch (i) { case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break; case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break; case 4: res = res.Sort(SortLevel.LOW_LEVEL); break; } //    . res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify(); } return res; } 

Ordeno el árbol aquí .

"Compilación" de funciones

Entre comillas, ya que no está en el código IL en sí, sino solo en un conjunto muy rápido de instrucciones. Pero es muy simple.

Problema sustituto

Para calcular el valor de una función, solo necesitamos llamar a la sustitución de variables y evaluar, por ejemplo

 var x = MathS.Var("x"); var expr = x * x + 3; var result = expr.Substitute(x, 5).Eval(); 

Pero funciona lentamente, aproximadamente 1,5 microsegundos por seno.

Instrucciones

Para acelerar el cálculo, hacemos un cálculo de función en la pila, a saber:

1) Creamos la clase FastExpression, que tendrá una lista de instrucciones

2) Al compilar, las instrucciones se apilan en el orden inverso, es decir, si hay una función x * x + sin (x) + 3, las instrucciones serán algo como esto:

 PUSHVAR 0 //    0 - x CALL 6 //    6 -  PUSHCONST 3 CALL 0 //    0 -  PUSHVAR 0 PUSHVAR 0 CALL 2 CALL 0 

Luego, cuando se nos llama, ejecutamos estas instrucciones y devolvemos el Número.

Un ejemplo de ejecución de una declaración de suma:

 internal static void Sumf(Stack<Number> stack) { Number n1 = stack.Pop(); Number n2 = stack.Pop(); stack.Push(n1 + n2); } 

La llamada sinusoidal se redujo de 1500ns a 60ns (el sistema Complex.Sin funciona durante 30ns).
El nabo se implementa aquí .

Fuh, todo parece ser por ahora. Aunque todavía hay algo que contar, pero me parece que el volumen de un artículo es suficiente. ¿Alguien está interesado en la secuela? A saber: analizar desde una cadena, formatear en látex, cierta integral y otras cosas.

Enlace al repositorio con todo el código, así como pruebas y muestras.


Gracias por su atencion!