Sobre algunos problemas de microoptimización

Antecedentes

Una vez, comenzó una conversación con un colega sobre la mejora de las herramientas para trabajar con marcas de bits en enumeraciones de C ++. En ese momento, ya teníamos la función IsEnumFlagSet, que toma la variable probada como el primer argumento y el segundo conjunto de indicadores para verificar. ¿Por qué es mejor que el buen viejo bitwise Y?

if (IsEnumFlagSet(state, flag)) { } // vs if (state & flag) { } 

En mi opinión, legibilidad. Raramente trabajo con indicadores de bit y operaciones de bit en general, así que cuando veo el código de otra persona es mucho más fácil percibir los nombres de funciones habituales que el críptico & | que llaman inmediatamente a la ventana interna.alert () con el encabezado "¡Atención! Puede haber algún tipo de magia sucediendo ".


Especialmente la legibilidad empeora durante las operaciones de configuración o eliminación de banderas. Compara:

 state |= flag; //    enum class,     |= state &= ~flag; //vs RaiseEnumFlag(state, flag); ClearEnumFlag(state, flag); 

Durante la discusión, también se expresó la idea de crear la función SetEnumFlag(state, flag, isSet) : dependiendo del tercer argumento, el state levantaría banderas o las SetEnumFlag(state, flag, isSet) .

Dado que se asumió que este argumento se pasa en RaiseEnumFlag/ClearEnumFlag de RaiseEnumFlag/ClearEnumFlag , obviamente, no puede prescindir de los gastos generales en comparación con el par RaiseEnumFlag/ClearEnumFlag . Pero en aras del interés académico, quería minimizarlo descendiendo a la mina al diablo de las micro optimizaciones.

Implementación

1. Implementación ingenua

Primero, presentamos nuestra enumeración (no utilizaremos la clase enum para simplificar):

 #include <limits> #include <random> enum Flags : uint32_t { One = 1u << 1, Two = 1u << 2, Three = 1u << 3, OneOrThree = One | Three, Max = 1u << 31, All = std::numeric_limits<uint32_t>::max() }; 

Y la implementación en sí:

 void SetFlagBranched(Flags& x, Flags y, bool cond) { if (cond) { x = Flags(x | y); } else { x = Flags(x & (~y)); } } 

2. Microoptimización

La implementación ingenua tiene una ramificación obvia, que me gustaría transferir a aritmética, que estamos tratando de hacer ahora.

Primero, necesitamos seleccionar alguna expresión que nos permita cambiar de un resultado a otro según el parámetro. Por ejemplo

 (x | y) & ¬p 

1. Cuando p = 0 levantamos las banderas:
   
   

    (x | y) & ¬0 ≡ (x | y) & 1 ≡ x | y 

   
   
2. Cuando p = y se eliminan p = y banderas:
   
   

    (x | y) & ¬y ≡ (x & ¬y) | (y & ¬y) ≡ (x & ¬y) | 0 ≡ x & ¬y 

   
   

Ahora necesitamos de alguna manera "empaquetar" en aritmética el cambio en el valor del parámetro dependiendo de la variable cond (recuerde: la ramificación está prohibida).

Deje p = y inicialmente, y si cond verdadero, intente restablecer p , si no, deje todo como está.

No podremos trabajar directamente con la variable cond : cuando se convierte al tipo aritmético, si es cierto, solo obtenemos una unidad en el orden inferior, e idealmente necesitamos unidades en todos los bits (UPD: aún puede ). Como resultado, no se me ocurrió nada mejor que usar cambios bit a bit.

Definimos la cantidad de cambio: no podemos cambiar inmediatamente todos nuestros bits para que el parámetro p restablezca en una operación, porque el estándar requiere que la cantidad de cambio sea menor que el tamaño de letra.


Por lo tanto, calculamos el tamaño máximo de turno, escribimos la expresión preliminar

 constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) * 8 - 1; (x | y) & ~ ( y >> shiftSize * cond); 

Y procese por separado el bit menos significativo del resultado de la expresión y >> shiftSize * cond :

 (x | y) & ~ (( y >> shiftSize * cond) & ~cond); 

La ramificación se shiftSize * cond en shiftSize * cond : dependiendo de falso o verdadero en cond, el valor de desplazamiento será 0 o 31, respectivamente, y nuestro parámetro será igual a y o 0.

Qué sucede cuando shiftSize = 31 :

1. Con cond = true desplazamos los bits y por 31 a la derecha, como resultado de lo cual el bit más significativo de y convierte en el menos significativo, y todo el resto se restablece a cero. In ~cond contrario, el bit menos significativo es 0, y todos los demás son uno. La multiplicación bit a bit de estos valores dará un 0 limpio.
2. Cuando cond = false no ocurre desplazamiento, ~cond en todos los dígitos tiene 1, y la multiplicación bit a bit de estos valores dará y .

Me gustaría señalar la compensación de este enfoque, que no es inmediatamente evidente: sin usar ramas, calculamos x | y x | y (es decir, una de las ramas de la versión ingenua) en cualquier caso, y luego, debido a las operaciones aritméticas "adicionales", la transformamos en el resultado deseado. Y todo esto tiene sentido si la sobrecarga de aritmética adicional es menor que la ramificación.

Entonces, la decisión final fue la siguiente:

 void SetFlagsBranchless(Flags& x, Flags y, bool cond) { constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) * 8 - 1; x = Flags((x | y) & ~(( y >> shiftSize * cond) & ~cond)); } 

(El tamaño del turno es más correcto para leer std::numeric_limits::digits , ver comentario )

3. Comparación

Habiendo implementado la solución sin ramificación, fui a quick-bench.com para asegurarme de su ventaja. Para el desarrollo, usamos principalmente clang, así que decidí ejecutar los puntos de referencia (clang-9.0). Pero entonces me esperaba una sorpresa ...



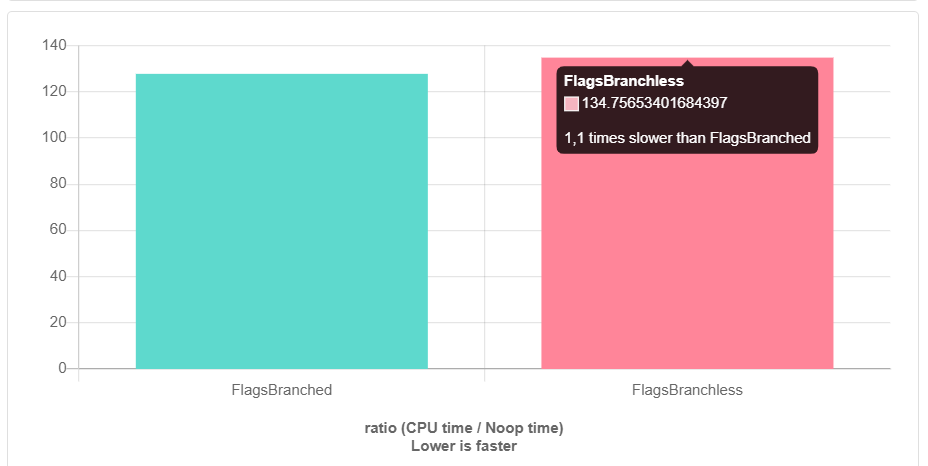
Y esto es con -O3. Sin optimizaciones, es peor. Como sucedio ¿Quién tiene la culpa y qué hacer?

Ordenamos "dejar a un lado el pánico" e ir a entender godbolt.org (quick-bench también proporciona una lista de asm, pero godbolt parece más conveniente a este respecto).

A continuación, solo hablaremos sobre el nivel de optimización -O3. Entonces, ¿qué código generó clang para nuestra implementación ingenua?

 SetFlagBranched(Flags&, Flags, bool): # @SetFlagBranched(Flags&, Flags, bool) mov eax, dword ptr [rdi] mov ecx, esi not ecx and ecx, eax or eax, esi test edx, edx cmove eax, ecx mov dword ptr [rdi], eax ret 

No está mal, ¿verdad? Clang también sabe cómo compensar, y entiende que será más rápido usar comandos de salto condicional para calcular ambas ramas y usar el comando de movimiento condicional, que no involucra el predictor de rama en el trabajo.

Código de implementación sin ramificación:

 SetFlag(Flags&, Flags, bool): # @SetFlag(Flags&, Flags, bool) mov eax, dword ptr [rdi] or eax, esi test edx, edx mov ecx, 31 cmove ecx, edx shr esi, cl not esi or esi, edx and esi, eax mov dword ptr [rdi], esi ret 

Casi "sin ramas" - Yo, por así decirlo, ordené la multiplicación habitual aquí, y usted, mi amigo, trajo un movimiento condicional. Tal vez el compilador tenga razón, y test + cmove en este caso será más rápido que imul, pero no soy tan bueno en ensamblador (personas conocedoras, dígame, por favor, en los comentarios).

Otra cosa es interesante: de hecho, para ambas implementaciones después de las optimizaciones, el compilador no generó exactamente lo que solicitamos, y como resultado obtuvimos algo intermedio: cmove se usa en ambas variantes, solo tenemos una gran cantidad de aritmética adicional en la implementación sin ramificación, lo que supera el punto de referencia.

Clang de la octava versión y versiones anteriores generalmente usa transiciones condicionales reales, "debido a lo cual" la versión "sin ramificación" se vuelve casi una vez y media más lenta:

 SetFlag(Flags&, Flags, bool): # @SetFlag(Flags&, Flags, bool) mov eax, dword ptr [rdi] or eax, esi mov cl, 31 test edx, edx jne .LBB0_2 xor ecx, ecx .LBB0_2: shr esi, cl not esi or esi, edx and eax, esi mov dword ptr [rdi], eax ret 

¿Qué conclusión se puede hacer? Además del obvio "no participe en la microoptimización innecesariamente", a menos que siempre pueda aconsejar verificar el resultado del trabajo en el código de la máquina, puede resultar que el compilador ya haya optimizado la versión inicial lo suficiente, y sus optimizaciones "ingeniosas" no lo entenderán, y a pesar de ello reflexionará condicionalmente transiciones en lugar de multiplicaciones.

En este punto, sería posible terminar, si no fuera por un "pero". El código gcc para la implementación ingenua es idéntico a la versión clang, pero la versión sin ramas.

 SetFlag(Flags&, Flags, bool): movzx edx, dl mov eax, esi or eax, DWORD PTR [rdi] mov ecx, edx sal ecx, 5 sub ecx, edx shr esi, cl not esi or esi, edx and esi, eax mov DWORD PTR [rdi], esi ret 

Respeto a los desarrolladores por una forma tan elegante de optimizar nuestra expresión sin usar imul o cmove . Lo que sucede aquí: la variable bool cond se desplaza a la izquierda 5 bits (porque el tipo de nuestra enumeración es uint32_t, su tamaño es de 32 bits, es decir, 100000 ₂ ), y luego se resta del resultado. Por lo tanto, obtenemos 11111 ₂ = 31 ₁₀ en el caso de cond = verdadero, y 0 en caso contrario. Huelga decir que tal opción es más rápida que la ingenua, incluso teniendo en cuenta su optimización de movimiento condicional.



Bueno, el resultado fue muy extraño: dependiendo del compilador, la opción sin ramas puede ser más rápida o más lenta que la implementación con ramas. Tratemos de ayudar a clang y transformar nuestra expresión usando el método gcc (al mismo tiempo simplifique la parte ~((y >> shiftSize * cond) & ~cond) acuerdo con De Morgan, esto se hace tanto por clang como por gcc):

 void SetFlagVerbose(Flags& x, Flags y, bool b) { constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) + 1; x = Flags( (x | y) & ( ~(y >> ((b << shiftSize) - b)) | b) ); } 

Tal sugerencia solo tiene efecto en la versión troncal de clang, donde realmente genera código similar a gcc (aunque en el original "sin ramificación" es la misma prueba + cmove)

¿Qué hay de MSVC? En ambas versiones, sin ramificación, se usa Imul honesto (no sé cuánto más rápido / más lento que la opción clang / gcc - quick-bench no es compatible con este compilador), y en la versión ingenua apareció el salto condicional. Triste pero cierto.

Resumen

Quizás se pueda llegar a la conclusión principal de que las intenciones del programador en el código de alto nivel están lejos de reflejarse siempre en el código de máquina, y esto hace que las microoptimizaciones no tengan sentido sin puntos de referencia y listas de visualización. Además, el resultado de las microoptimizaciones puede ser mejor o peor que la versión habitual: todo depende del compilador, lo que puede ser un problema grave si el proyecto es multiplataforma.