Experimentos con redes neuronales basadas en datos sísmicos.

La complejidad de la interpretación de los datos sísmicos se debe al hecho de que para cada tarea es necesario buscar un enfoque individual, ya que cada conjunto de dichos datos es único. El procesamiento manual requiere costos laborales significativos, y el resultado a menudo contiene errores relacionados con el factor humano. El uso de redes neuronales para la interpretación puede reducir significativamente el trabajo manual, pero la singularidad de los datos impone restricciones en la automatización de este trabajo.

Este artículo describe un experimento para analizar la aplicabilidad de las redes neuronales para automatizar la asignación de capas geológicas en imágenes 2D utilizando como ejemplo datos completamente etiquetados del Mar del Norte.


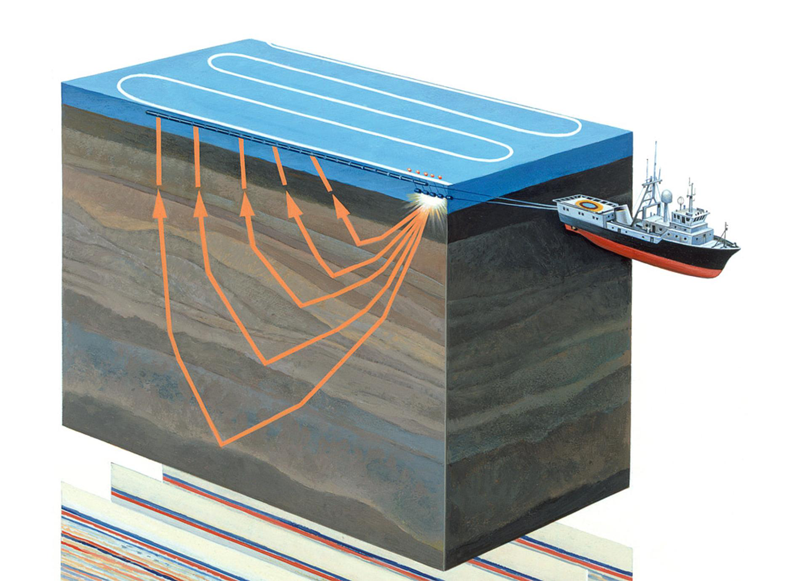
Figura 1. Encuestas sísmicas acuatoriales ( fuente )

Un poco sobre el tema

La exploración sísmica es un método geofísico para estudiar objetos geológicos utilizando vibraciones elásticas: ondas sísmicas. Este método se basa en el hecho de que la velocidad de propagación de las ondas sísmicas depende de las propiedades del entorno geológico en el que se propagan (composición de la roca, porosidad, fractura, saturación de humedad, etc.) Al pasar a través de capas geológicas con diferentes propiedades, las ondas sísmicas se reflejan desde diferentes objetos y devueltos al receptor (ver Figura 1). Su naturaleza se registra y después del procesamiento le permite formar una imagen bidimensional, una sección sísmica o una matriz de datos tridimensional, un cubo sísmico.


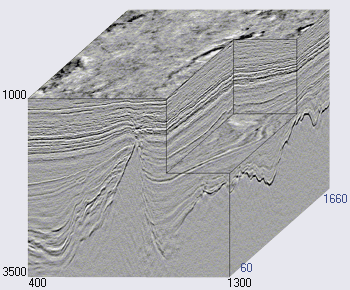
Figura 2. Un ejemplo de un cubo sísmico ( fuente )

El eje horizontal del cubo sísmico se encuentra a lo largo de la superficie de la tierra, y el vertical representa la profundidad o el tiempo (ver Figura 2). En algunos casos, el cubo se divide en secciones verticales a lo largo del eje de los geófonos (las llamadas líneas, líneas) o cruzadas (líneas cruzadas, líneas cruzadas, líneas x). Cada cubo vertical (y corte) es un rastro sísmico separado.

Por lo tanto, las líneas y líneas cruzadas consisten en los mismos senderos sísmicos, solo en un orden diferente. Los senderos sísmicos adyacentes son muy similares entre sí. Un cambio más dramático ocurre en los puntos de falla, pero aún habrá similitudes. Esto significa que los sectores vecinos son muy similares entre sí.

Todo este conocimiento nos será útil al planificar experimentos.

La tarea de interpretación y el papel de las redes neuronales en su solución.

Los datos obtenidos son procesados ​​manualmente por intérpretes que identifican directamente en el cubo o en cada corte sus capas geológicas individuales de rocas y sus límites (horizontes, horizontes), depósitos de sal, fallas y otras características de la estructura geológica del área de estudio. El intérprete, trabajando con un cubo o una rodaja, comienza su trabajo con una minuciosa selección manual de capas geográficas y horizontes. Cada horizonte debe ser picado manualmente (del inglés "picking" - colección) apuntando el cursor y haciendo clic con el mouse.


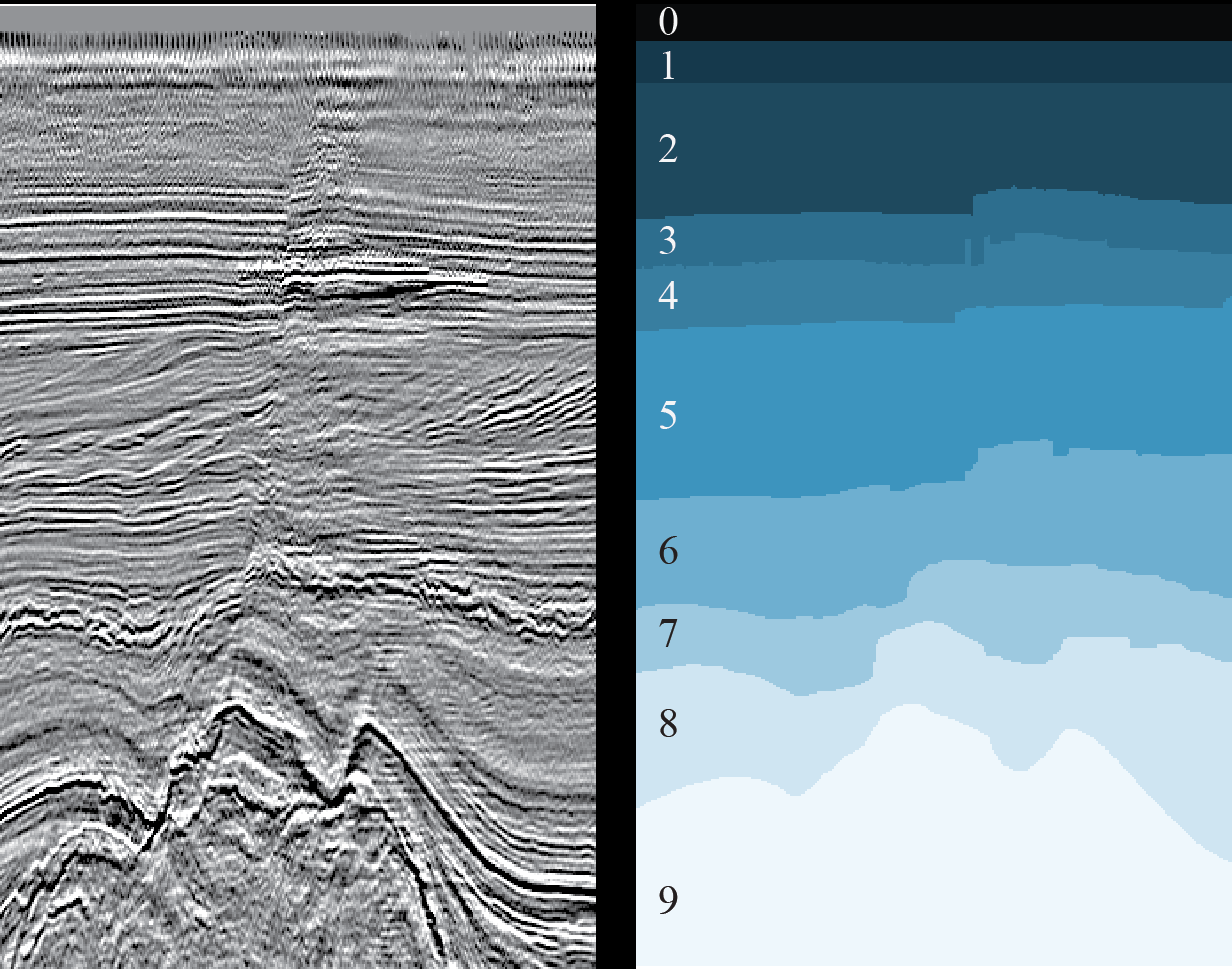
Figura 3. Un ejemplo de un corte 2D (izquierda) y el resultado del marcado de las capas geológicas correspondientes (derecha) ( fuente )

El principal problema está relacionado con el creciente volumen de datos sísmicos obtenidos cada año en condiciones geológicas cada vez más complejas (por ejemplo, secciones submarinas con grandes profundidades del mar), y la ambigüedad de la interpretación de estos datos. Además, en condiciones de plazos ajustados y / o grandes volúmenes, el intérprete inevitablemente comete errores, por ejemplo, pierde varias características de la sección geológica.

Este problema puede resolverse parcialmente con la ayuda de redes neuronales, reduciendo significativamente el trabajo manual, acelerando así el proceso de interpretación y reduciendo el número de errores. Para el funcionamiento de la red neuronal, se requiere un cierto número de secciones (secciones del cubo) etiquetadas y preparadas, y como resultado se obtendrá una marca completa de todas las secciones (o el cubo completo), lo que idealmente requerirá solo un refinamiento menor por parte de una persona para ajustar ciertas secciones de los horizontes o volver a marcar áreas pequeñas que la red no pudo reconocer correctamente.

Hay muchas soluciones a los problemas de interpretación usando redes neuronales, aquí hay solo algunos ejemplos: uno , dos , tres . La dificultad radica en el hecho de que cada conjunto de datos es único, debido a las peculiaridades de las rocas geológicas de la región estudiada, debido a diversos medios técnicos y métodos de exploración sísmica, a causa de los diversos métodos utilizados para convertir los datos sin procesar en preparados. Incluso debido a ruidos externos (por ejemplo, un perro ladrando y otros sonidos fuertes), que no siempre es posible eliminar por completo. Por lo tanto, cada tarea debe resolverse individualmente.

Pero, a pesar de esto, numerosos trabajos permiten buscar enfoques generales separados para resolver diversos problemas de interpretación.

En MaritimeAI (un proyecto desarrollado a partir de la comunidad ODS de Machine Learning for Social Goods, un artículo sobre nosotros ) para cada zona de nuestro campo de interés (investigación marina) estudiamos trabajos ya publicados y realizamos nuestros propios experimentos, lo que nos permite aclarar los límites y las características de la aplicación de ciertos soluciones, y a veces encuentra tus propios enfoques.

Los resultados de un experimento que describimos en este artículo.

Objetivos de investigación empresarial

Es suficiente que un especialista en ciencia de datos eche un vistazo a la Figura 3 para dar un suspiro de alivio, una tarea común de segmentación de imágenes semánticas, para la cual se han inventado muchas arquitecturas de redes neuronales y métodos de enseñanza. Solo necesita elegir los correctos y capacitar a la red.

Pero no tan simple.

Para obtener un buen resultado con la ayuda de una red neuronal, necesita la mayor cantidad posible de datos ya marcados sobre los que aprenderá. Pero nuestra tarea es precisamente reducir la cantidad de trabajo manual. Y rara vez es posible utilizar datos etiquetados de otras regiones debido a sus fuertes diferencias en la estructura geológica.

Traducimos lo anterior al lenguaje de los negocios.

Para que el uso de redes neuronales se justifique económicamente, es necesario minimizar la cantidad de interpretación manual primaria y los refinamientos de los resultados obtenidos. Pero reducir los datos para capacitar a la red afectará negativamente la calidad de su resultado. Entonces, ¿puede una red neuronal acelerar y facilitar el trabajo de los intérpretes y mejorar la calidad de las imágenes etiquetadas? ¿O simplemente complicar el proceso habitual?

El objetivo de este estudio es intentar determinar el volumen mínimo suficiente de datos de cubos sísmicos marcados para una red neuronal y evaluar los resultados obtenidos. Intentamos encontrar respuestas a las siguientes preguntas, que deberían ayudar a los "propietarios" de los resultados de la encuesta sísmica a decidir sobre la interpretación manual o parcialmente automatizada:

1. ¿Cuántos datos necesitan marcar los expertos para entrenar una red neuronal? ¿Y qué datos se deben elegir para esto?
2. ¿Qué pasa con tal salida? ¿Será necesario el refinamiento manual de las predicciones de la red neuronal? Si es así, ¿qué tan complejo y voluminoso?

Descripción general del experimento y los datos utilizados.

Para el experimento, seleccionamos uno de los problemas de interpretación, a saber, la tarea de aislar capas geológicas en secciones 2D de un cubo sísmico (ver Figura 3). Ya hemos tratado de resolver este problema (ver aquí ) y, según los autores, obtuvimos un buen resultado para el 1% de los cortes seleccionados al azar. Dado el volumen del cubo, estas son 16 imágenes. Sin embargo, el artículo no proporciona métricas de comparación y no hay una descripción de la metodología de entrenamiento (función de pérdida, optimizador, esquema para cambiar la velocidad de aprendizaje, etc.), lo que hace que el experimento sea irreproducible.

Además, los resultados presentados allí, en nuestra opinión, son insuficientes para obtener respuestas completas a las preguntas planteadas. ¿Es este valor óptimo al 1%? ¿O tal vez para otra muestra de rebanadas será diferente? ¿Puedo seleccionar menos datos? ¿Vale la pena tomar más? ¿Cómo cambiará el resultado? Etc.

Para el experimento, tomamos el mismo conjunto de datos completamente etiquetados del sector holandés del Mar del Norte. Los datos sísmicos de origen están disponibles en el sitio web Open Seismic Repository: Project Netherlands Offshore F3 Block . Una breve descripción se puede encontrar en Silva et al. "Conjunto de datos de los Países Bajos: un nuevo conjunto de datos públicos para el aprendizaje automático en la interpretación sísmica" .

Como en nuestro caso estamos hablando de cortes 2D, no utilizamos el cubo 3D original, sino el "corte" ya hecho, disponible aquí: Conjunto de datos de interpretación F3 de Holanda .

Durante el experimento, resolvimos las siguientes tareas:

1. Observamos los datos de origen y seleccionamos los cortes, que son los más cercanos en calidad a la marca manual.
2. Registramos la arquitectura de la red neuronal, la metodología y los parámetros de entrenamiento, y el principio de seleccionar cortes para entrenamiento y validación.
3. Entrenamos 20 redes neuronales idénticas en diferentes volúmenes de datos del mismo tipo de cortes para comparar los resultados.
4. Capacitamos a otras 20 redes neuronales en una cantidad diferente de datos de diferentes tipos de cortes para comparar los resultados.
5. Estimación de la cantidad de refinamiento manual necesario de los resultados del pronóstico.

A continuación se presentan los resultados del experimento en forma de métricas estimadas y predichas por las redes de máscaras de corte.

Tarea 1. Selección de datos

Entonces, como datos iniciales, utilizamos líneas y líneas cruzadas ya preparadas del cubo sísmico del sector holandés del Mar del Norte. Un análisis detallado mostró que todo no funciona sin problemas: hay muchas imágenes y máscaras con artefactos e incluso con distorsiones graves (ver Figuras 4 y 5).


Figura 4. Ejemplo de máscara con artefactos


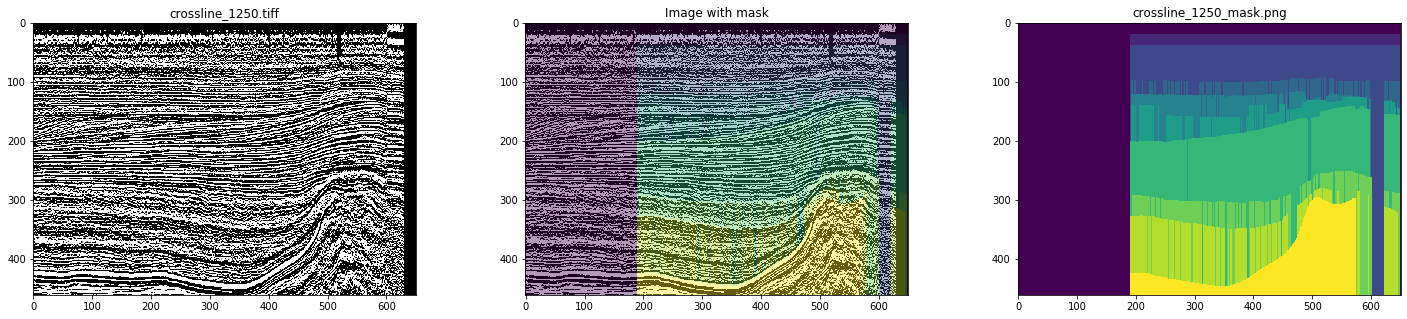
Figura 5. Un ejemplo de una máscara distorsionada

Con el marcado manual, no se observará nada por el estilo. Por lo tanto, simulando el trabajo del intérprete, para capacitar a la red, elegimos solo máscaras limpias, después de haber examinado todas las secciones. Como resultado, se seleccionaron 700 líneas cruzadas y 400 líneas.

Tarea 2. Fijar los parámetros del experimento.

Esta sección es de interés, en primer lugar, para los especialistas en ciencia de datos, por lo tanto, se utilizará la terminología adecuada.

Dado que las líneas y las líneas cruzadas consisten en las mismas huellas sísmicas, se pueden proponer dos hipótesis mutuamente excluyentes:

1. La capacitación se puede llevar a cabo solo en un tipo de sectores (por ejemplo, en línea), utilizando imágenes de otro tipo como una selección retrasada. Esto dará una evaluación más adecuada del resultado, porque las rebanadas restantes del mismo tipo que se usaron en el entrenamiento seguirán siendo similares a las del entrenamiento.
2. Para el entrenamiento, es mejor usar una mezcla de rebanadas de diferentes tipos, ya que este es un aumento listo para usar.

Compruébalo

Además, la similitud de los sectores vecinos del mismo tipo y el deseo de obtener un resultado reproducible nos llevaron a una estrategia para seleccionar sectores para el entrenamiento y la validación, no por un principio arbitrario, sino de manera uniforme en todo el cubo, es decir. para que los sectores estén lo más separados posible y, por lo tanto, cubran la máxima variedad de datos.

Para la validación, se utilizaron 2 cortes, también distribuidos equitativamente entre imágenes adyacentes de la muestra de entrenamiento. Por ejemplo, para el caso de una muestra de entrenamiento de 3 líneas, la muestra de validación consistió en 4 líneas, para 3 líneas y 3 líneas cruzadas, de 8 cortes, respectivamente.

Como resultado, realizamos 2 series de entrenamientos:

1. Capacitación en muestras de líneas en línea de 3 a 20 rebanadas distribuidas uniformemente en el cubo con verificación del resultado de las predicciones de la red en las líneas restantes y en todas las líneas cruzadas. Además, se realizó capacitación en 80 y 160 secciones.
2. Capacitación en muestras combinadas de líneas en línea y cruzadas de 3-10 secciones de cada tipo distribuidas uniformemente en un cubo con verificación del resultado de las predicciones de la red en las imágenes restantes. Además, la capacitación se realizó en 40 + 40 y 80 + 80 secciones.

Con este enfoque, es necesario tener en cuenta que los tamaños de las muestras de capacitación y validación varían significativamente, lo que dificulta la comparación, pero el volumen de las imágenes restantes no se reduce tanto que puede usarse para una evaluación adecuada de los cambios en el resultado.

Para reducir el reentrenamiento para la muestra de entrenamiento, se utilizó el aumento con un tamaño de cultivo arbitrario de 448x64 y una imagen especular a lo largo del eje vertical con una probabilidad de 0.5.

Dado que estamos interesados ​​en la dependencia de la calidad del resultado solo en el número de cortes en la muestra de entrenamiento, se puede descuidar el preprocesamiento de las imágenes. Utilizamos una sola capa de imágenes PNG sin ningún cambio.

Por la misma razón, en el marco de este experimento, no hay necesidad de buscar la mejor arquitectura de red: lo principal es que sea lo mismo en cada paso. Elegimos un UNet simple pero bien establecido para tales tareas:


Figura 6. Arquitectura de red

La función de pérdida consistió en una combinación del coeficiente Jacquard y la entropía cruzada binaria:

def jaccard_loss(y_true, y_pred): smoothing = 1. intersection = tf.reduce_sum(y_true * y_pred, axis = (1, 2)) union = tf.reduce_sum(y_true + y_pred, axis = (1, 2)) jaccard = (intersection + smoothing) / (union - intersection + smoothing) return 1. - tf.reduce_mean(jaccard) def loss(y_true, y_pred): return 0.75 * jaccard_loss(y_true, y_pred) + 0.25 * keras.losses.binary_crossentropy(y_true, y_pred) 

Otras opciones de aprendizaje:

 keras.optimizers.SGD(lr = 0.01, momentum = 0.9, nesterov = True) keras.callbacks.EarlyStopping(monitor = 'val_loss', patience = 10), keras.callbacks.ReduceLROnPlateau(monitor = 'val_loss', patience = 5) 

Para reducir la influencia de la aleatoriedad de la elección de los pesos iniciales en los resultados, la red se capacitó en 3 líneas durante 1 era. Todos los demás entrenamientos comenzaron con estos pesos recibidos.

Cada red fue entrenada en GeForce GTX 1060 6Gb durante 30-60 épocas. El entrenamiento de cada época tomó 10-30 segundos dependiendo del tamaño de la muestra.

Tarea 3. Capacitación en un tipo de rebanadas (en línea)

La primera serie consistió en 18 capacitaciones de redes independientes en 3-20 líneas en línea. Y, aunque solo estamos interesados ​​en estimar el coeficiente Jacquard en cortes que no se usan en el entrenamiento y la validación, es interesante considerar todos los gráficos.

Recuerde que los resultados de interpretación para cada segmento son 10 clases (capas geológicas), que en las figuras están marcadas con números del 0 al 9.


Figura 7. Coeficiente Jacquard para el conjunto de entrenamiento.


Figura 8. Coeficiente de Jacquard para la muestra de validación


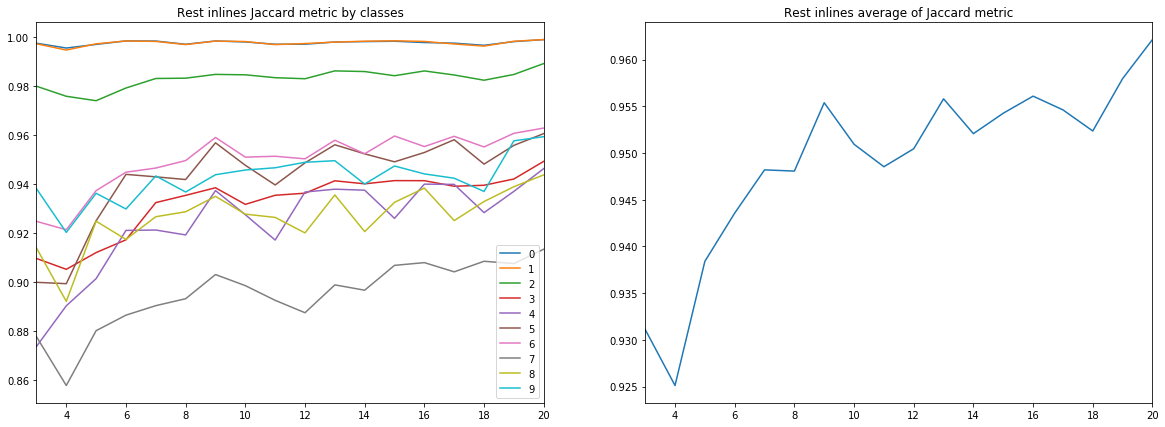
Figura 9. Coeficiente de Jacquard para las líneas restantes


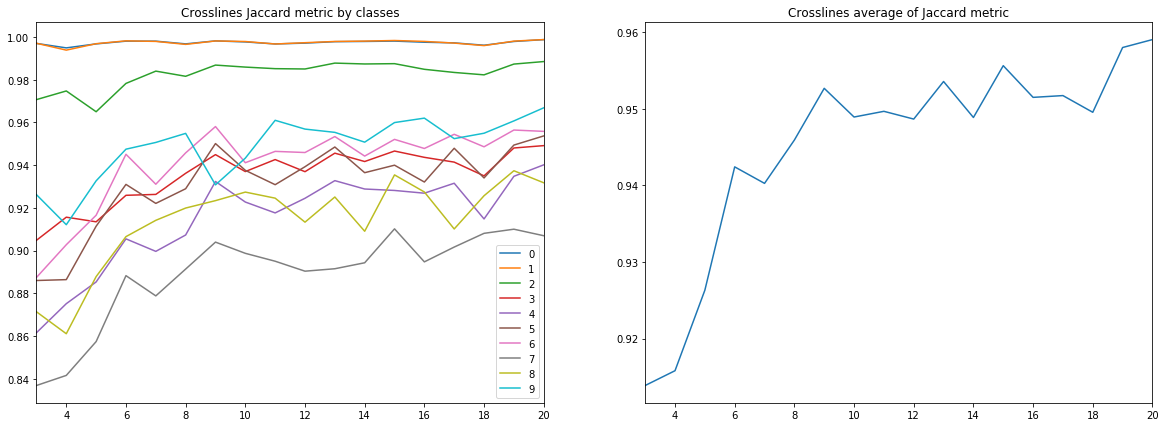
Figura 10. Coeficiente de Jacquard para líneas cruzadas

Se pueden extraer varias conclusiones de los diagramas anteriores.

En primer lugar, la calidad del pronóstico, medida por el coeficiente Jacquard, ya en 9 líneas alcanza un valor muy alto, después de lo cual continúa creciendo, pero no tan intensamente. Es decir Se confirma la hipótesis de la suficiencia de un pequeño número de imágenes etiquetadas para entrenar una red neuronal.

En segundo lugar, se obtuvo un resultado muy alto para las líneas cruzadas, a pesar de que solo se usaron líneas en línea para el entrenamiento y la validación; también se confirma la hipótesis de la suficiencia de un solo tipo de cortes. Sin embargo, para la conclusión final, debe comparar los resultados con el entrenamiento en una mezcla de líneas y líneas cruzadas.

En tercer lugar, las métricas para diferentes capas, es decir La calidad de su reconocimiento es muy diferente. Esto lleva a la idea de elegir una estrategia de aprendizaje diferente, por ejemplo, usar pesos o redes adicionales para clases débiles, o un esquema completo de "uno contra todos".

Y finalmente, debe tenerse en cuenta que el coeficiente Jacquard no puede proporcionar una descripción completa de la calidad del resultado. Para evaluar las predicciones de la red en este caso, es mejor mirar las máscaras para evaluar su idoneidad para la revisión por parte del intérprete.

Las siguientes figuras muestran el marcado por una red capacitada en 10 líneas. La segunda columna, marcada como "máscara GT" (máscara de verdad del terreno), representa la interpretación del objetivo, la tercera es la predicción de la red neuronal.



Figura 11. Ejemplos de pronósticos de red para inlines



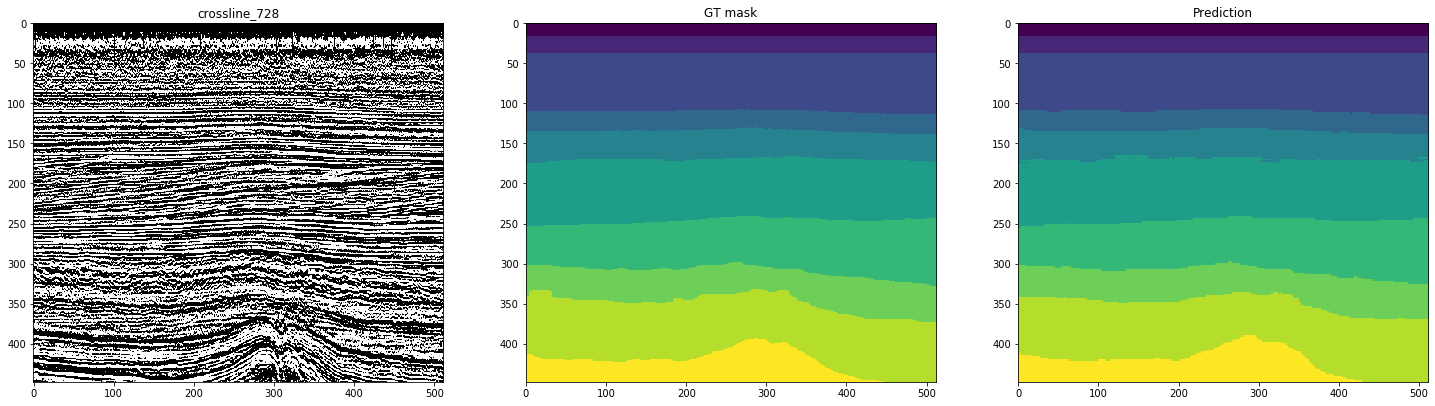
Figura 12. Ejemplos de pronósticos de red para líneas cruzadas

Se puede ver en las cifras que, junto con máscaras bastante limpias, la red es difícil de reconocer casos complejos incluso en las propias líneas. Por lo tanto, a pesar de la métrica lo suficientemente alta para 10 cortes, parte de los resultados requerirán un refinamiento significativo.

Los tamaños de muestra considerados por nosotros fluctúan alrededor del 1% del volumen total de datos, y esto ya hace posible marcar bastante bien parte de los cortes restantes. ¿Debo aumentar el número de secciones marcadas inicialmente? ¿Esto dará un aumento comparable en la calidad?

Consideremos la dinámica de los cambios en los resultados del pronóstico por redes capacitadas en 5, 10, 15, 20, 80 (5% del volumen total del cubo) y 160 (10%) en línea usando las mismas secciones como ejemplo.


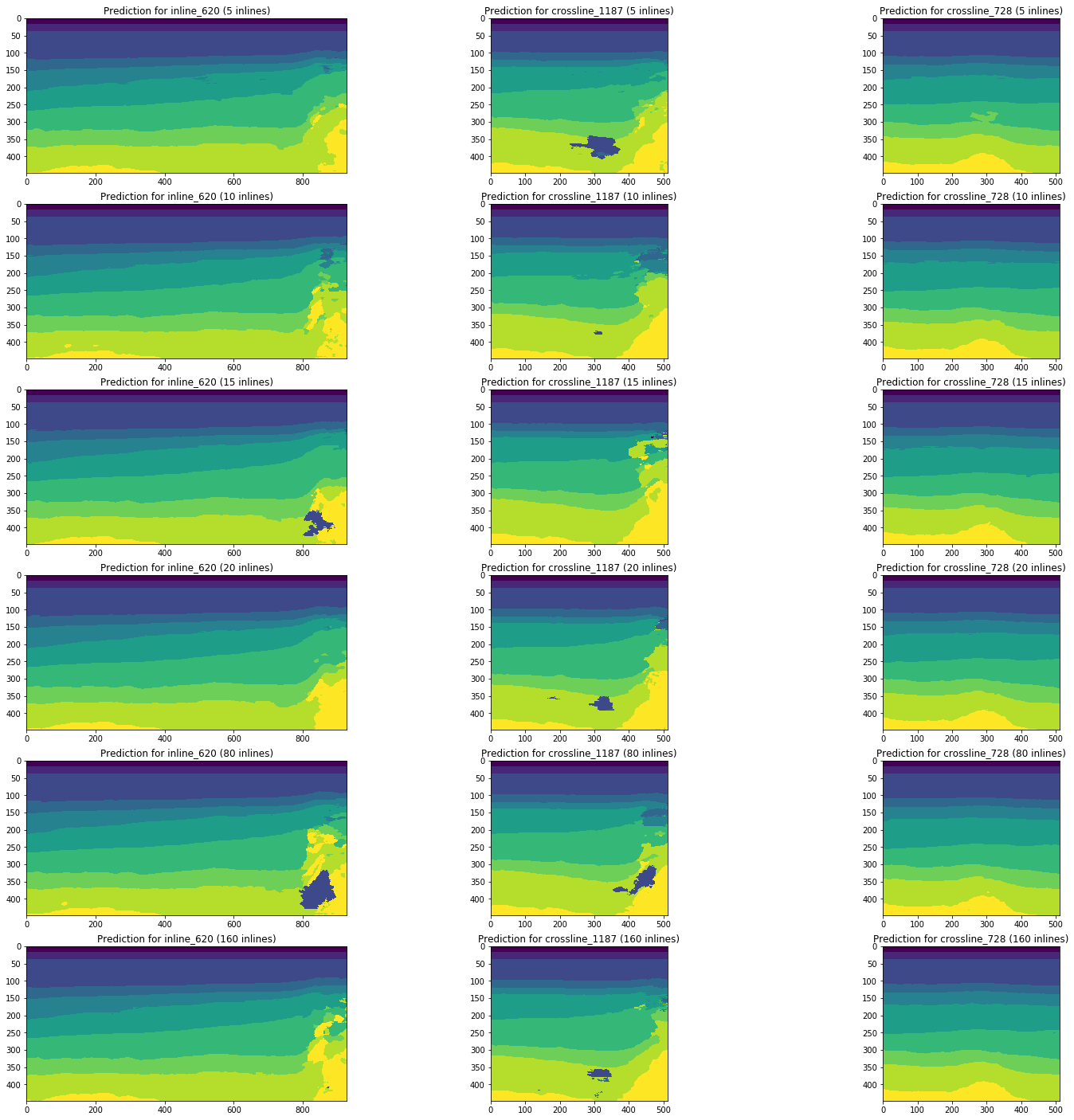
Figura 13. Ejemplos de pronósticos de redes capacitadas en diferentes volúmenes de la muestra de capacitación.

La Figura 13 muestra que un aumento en el volumen de la muestra de entrenamiento en 5 o incluso 10 veces no conduce a una mejora significativa. Los cortes que ya están bien reconocidos en 10 imágenes de entrenamiento no empeoran.

Por lo tanto, incluso una red simple sin ajuste y procesamiento previo de imágenes es capaz de interpretar parte de los cortes con una calidad suficientemente alta con un pequeño número de imágenes marcadas manualmente. Consideraremos la cuestión de la parte de tales interpretaciones y la complejidad de finalizar cortes poco reconocidos.

Una cuidadosa selección de arquitectura, parámetros de red y capacitación, el preprocesamiento de imágenes puede mejorar estos resultados en el mismo volumen de datos etiquetados. Pero esto ya está más allá del alcance del experimento actual.

Tarea 4. Capacitación en diferentes tipos de sectores (líneas y líneas cruzadas)

Ahora comparemos los resultados de esta serie con los pronósticos obtenidos al entrenar en una mezcla de líneas y líneas cruzadas.

Los diagramas a continuación muestran estimaciones del coeficiente Jacquard para diferentes muestras, incluso, en comparación con los resultados de las series anteriores. Para comparar (ver los diagramas correctos en las figuras), solo se tomaron muestras del mismo volumen, es decir 10 líneas en línea vs 5 líneas en línea + 5 líneas cruzadas, etc.


Figura 14. Coeficiente Jacquard para el conjunto de entrenamiento.


Figura 15. Coeficiente de Jacquard para la muestra de validación


Figura 16. Coeficiente de Jacquard para las líneas restantes


Figura 17. Coeficiente Jacquard para las líneas cruzadas restantes

Los diagramas ilustran claramente que agregar segmentos de un tipo diferente no mejora los resultados. Incluso en el contexto de las clases (ver Figura 18), no se observa la influencia de las líneas cruzadas para ninguno de los tamaños de muestra considerados.


Figura 18. Coeficiente de Jacquard para diferentes clases (a lo largo del eje X) y diferentes tamaños y composición de la muestra de entrenamiento.

Para completar la imagen, comparamos los resultados del pronóstico de la red en los mismos segmentos:


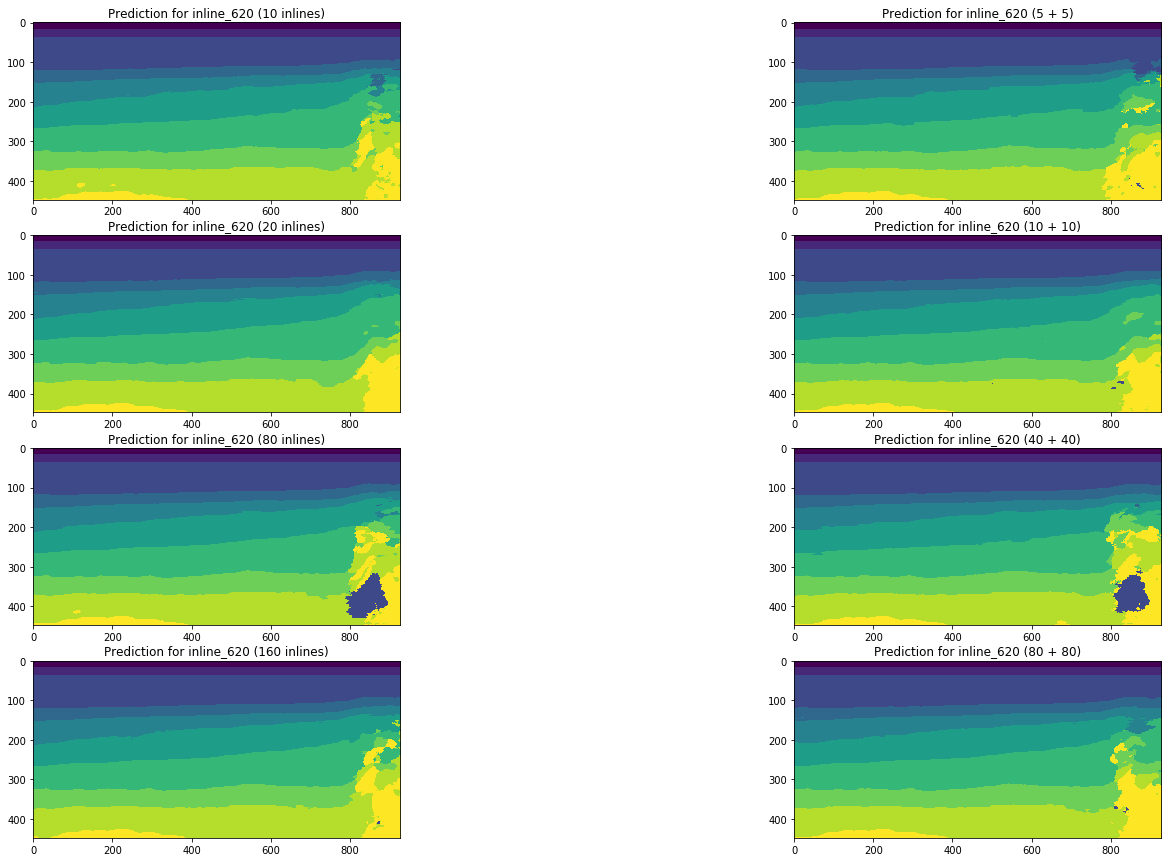
Figura 19. Comparación de pronósticos de red para línea


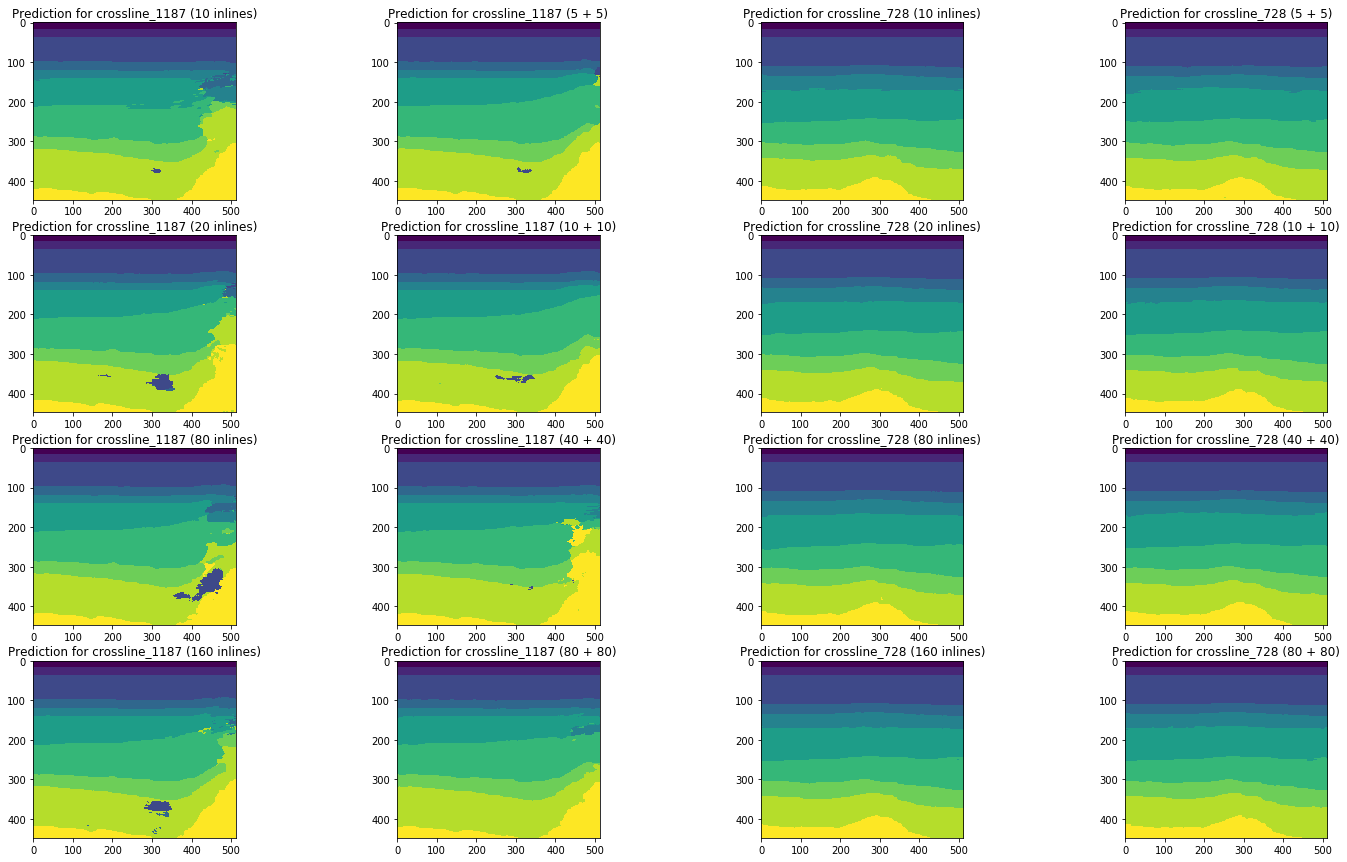
Figura 20. Comparación de pronósticos de red para líneas cruzadas

Una comparación visual confirma la suposición de que agregar diferentes tipos de rebanadas a la capacitación no cambia fundamentalmente la situación. Algunas mejoras solo se pueden observar para la línea de cruce izquierda, pero ¿son globales? Intentaremos responder esta pregunta más adelante.

Tarea 5. Evaluación del volumen de refinamiento manual.

Para una conclusión final sobre los resultados, es necesario estimar la cantidad de refinamiento manual de los pronósticos de red obtenidos. Para hacer esto, determinamos el número de componentes conectados (es decir, puntos sólidos del mismo color) en cada pronóstico obtenido. Si este valor es 10, las capas se seleccionan correctamente y estamos hablando de un máximo de corrección menor del horizonte. Si no hay muchos más, solo necesita "limpiar" las áreas pequeñas de la imagen. Si hay sustancialmente más de ellos, entonces todo es malo e incluso puede necesitar un rediseño completo.

Para las pruebas, seleccionamos 110 líneas y 360 líneas cruzadas que no se utilizaron en la capacitación de ninguna de las redes consideradas.

Tabla 1. Estadísticas promediadas sobre ambos tipos de sectores


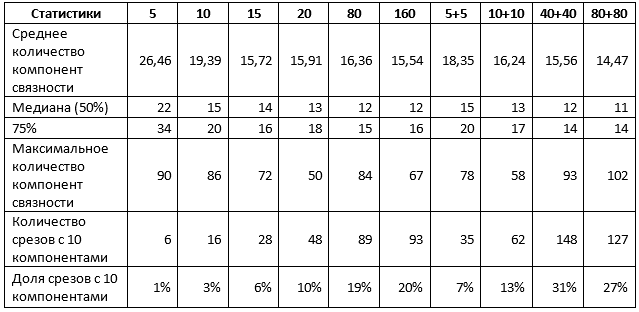
La Tabla 1 confirma algunos de los resultados anteriores. En particular, cuando se usan 1% de cortes para el entrenamiento, no hay diferencia, use un tipo de cortes o ambos, y el resultado se puede caracterizar de la siguiente manera:

• alrededor del 10% de los pronósticos son cercanos al ideal, es decir no requieren más que ajustes a secciones individuales de los horizontes;
• El 50% de los pronósticos no contienen más de 15 puntos, es decir no más de 5 extra;
• El 75% de los pronósticos no contienen más de 20 puntos, es decir no más de 10 extra;
• el 25% restante de las previsiones requieren un refinamiento más sustancial, incluido, posiblemente, un rediseño completo de sectores individuales.

Un aumento en el tamaño de la muestra de hasta un 5% cambia la situación. En particular, las redes capacitadas en una mezcla de secciones muestran indicadores significativamente más altos, aunque el valor máximo de los componentes también aumenta, lo que indica la aparición de interpretaciones separadas de muy baja calidad. Sin embargo, si aumenta la muestra 5 veces y usa una mezcla de rebanadas:

• Alrededor del 30% de los pronósticos son casi ideales, es decir no requieren más que ajustes a secciones individuales de los horizontes;
• El 50% de los pronósticos no contienen más de 12 puntos, es decir no más de 2 extra;
• El 75% de los pronósticos no contienen más de 14 puntos, es decir no más de 4 extra;
• el 25% restante de las previsiones requieren un refinamiento más sustancial, incluido, posiblemente, un rediseño completo de sectores individuales.

Un aumento adicional en el tamaño de la muestra no conduce a mejores resultados.

En general, para el cubo de datos que examinamos, podemos sacar conclusiones sobre la suficiencia del 1-5% del volumen total de datos para obtener un buen resultado de una red neuronal.

Según dichos datos, junto con las métricas e ilustraciones anteriores, ya es posible sacar conclusiones sobre la conveniencia de utilizar redes neuronales para ayudar a los intérpretes y sobre los resultados con los que se enfrentarán los especialistas.

Conclusiones

Entonces, ahora podemos responder las preguntas formuladas al comienzo del artículo, utilizando los resultados obtenidos en el ejemplo de un cubo sísmico del Mar del Norte:

¿Cuántos datos necesitan marcar los expertos para entrenar una red neuronal? ¿Y qué datos debo elegir?

Para obtener un buen pronóstico de la red, es realmente suficiente marcar previamente el 1-5% del número total de cortes. Un aumento adicional en el volumen no conduce a una mejora en el resultado, comparable con el aumento en el número de datos previamente marcados. Para obtener un mejor marcado en un volumen tan pequeño utilizando una red neuronal, debe probar otros enfoques, por ejemplo, ajustar la arquitectura y las estrategias de aprendizaje, preprocesamiento de imágenes, etc.

Para el marcado preliminar, vale la pena elegir sectores de ambos tipos: líneas y líneas cruzadas.

¿Qué pasa con tal salida? ¿Será necesario el refinamiento manual de las predicciones de la red neuronal? Si es así, ¿qué tan complejo y voluminoso?

Como resultado, una parte importante de las imágenes etiquetadas por dicha red neuronal no requerirá el refinamiento más significativo, que consiste en la corrección de zonas individuales poco reconocidas. Entre ellos habrá tales interpretaciones que no requerirán ninguna corrección. Y solo para imágenes individuales, es posible que necesite un nuevo diseño manual.

Por supuesto, al optimizar el algoritmo de aprendizaje y los parámetros de red, se pueden mejorar sus capacidades predictivas. En nuestro experimento, no se incluyó la solución de tales problemas.

Además, los resultados de un estudio en un cubo sísmico no deben generalizarse sin pensar, precisamente debido a la singularidad de cada conjunto de datos. Pero estos resultados son la confirmación de un experimento realizado por otros autores, y la base para la comparación con nuestros estudios posteriores, sobre los que también escribiremos en breve.

Agradecimientos

Y al final, me gustaría agradecer a mis colegas de MaritimeAI (especialmente Andrey Kokhan) y ODS por sus valiosos comentarios y ayuda.

Lista de fuentes utilizadas:

1. Bas Peters, Eldad Haber, Justin Granek. Redes neuronales para geofísicos y su aplicación a la interpretación de datos sísmicos
2. Hao Wu, Bo Zhang. Una profunda red neuronal codificador-decodificador convolucional para ayudar al seguimiento del horizonte sísmico
3. Thilo Wrona, Indranil Pan, Robert L. Gawthorpe y Haakon Fossen. Análisis sísmico de facies utilizando aprendizaje automático
4. Reinaldo Mozart Silva, Lais Baroni, Rodrigo S. Ferreira, Daniel Civitarese, Daniela Szwarcman, Emilio Vital Brasil. Conjunto de datos de los Países Bajos: un nuevo conjunto de datos públicos para el aprendizaje automático en la interpretación sísmica