⛴️ 🍺 👨‍🎤 Problema de finalización de n-Queens: algoritmo de solución lineal 🥗 🧕🏼 🌐

Ericgrig

Prólogo

Me gustaría comenzar el prefacio con palabras de agradecimiento a dos maravillosos programadores de Odessa: Andrei Kiper (Lohica) y Timur Giorgadze (Luxoft), para una verificación independiente de mis resultados, en la etapa inicial del estudio.

El artículo "Algoritmo lineal para la solución del problema de finalización de n-Queens" se publicó en (arXiv.org) a principios del primer día de 2020. Inicialmente, el artículo fue escrito en ruso, por lo que la presentación básica se presenta aquí y existe la traducción.
Esta tarea, y alguna otra de los muchos conjuntos NP-completos (la tarea de satisfacer fórmulas booleanas (3-SAT), la tarea de encontrar la camarilla máxima, o una camarilla de un tamaño determinado ...) en diferentes momentos, estaban en mi área de interés. Estaba buscando una solución algorítmica basada en varios experimentos computacionales, pero no hubo un éxito concreto. Era como una persona tratando de aprender a ponerse en forma en la barra horizontal de un brazo. No hay resultado, pero cada vez hay una esperanza de que todo salga pronto. La última vez que decidí que debía quedarme más tiempo en la tarea de finalización de n-Queens (como uno de los miembros de la familia) e intentar hacer algo. Aquí es apropiado recordar la maravillosa broma de Odessa: "En un autobús lleno de gente que regresa a los suburbios en una carretera llena de baches por la noche, se escucha la voz de una mujer: hombre, si me has acostado por completo, haz al menos algo".
El estudio duró lo suficiente, casi un año y medio. Por un lado, esto se debe al hecho de que se consideraron otras tareas en el proceso de investigación, y por otro, hubo preguntas difíciles en el camino, sin las cuales no podríamos avanzar. Voy a enumerar algunos de ellos:
- Hay n filas en la matriz de decisión, ¿en qué secuencia se debe seleccionar el índice de fila si el número de posibilidades para esta elección es n!
- cuando se hace una fila, ¿cuál de las posiciones libres restantes en esta fila debe seleccionarse, porque el número de posibilidades para tal selección es tan grande que puede considerarse un "pariente cercano" del infinito (por ejemplo, el número de formas posibles de seleccionar una posición libre en todas las filas para un tablero de ajedrez de tamaño 100 x 100 es aproximadamente ¹⁰¹²⁴ )
- Juntos, estos dos indicadores forman un espacio de estado (un espacio de elección). Parece que hay grandes oportunidades, puedes elegir lo que quieras. Pero detrás de cada elección específica en cada paso, hay otro problema: la limitación de la elección en todos los pasos posteriores. Además, esto es especialmente sensible en las últimas etapas de resolución del problema. Podemos decir que la matriz de decisión es "vengativa". Todos los "errores inconscientes" que cometes al hacer una elección en las etapas anteriores se "acumulan", y al final de la decisión esto se manifiesta en el hecho de que en esas líneas donde debes colocar a la reina, no hay posiciones vacías y la rama de búsqueda se detiene. . Aquí, como con Zhvanetsky: "un movimiento equivocado y estás embarazada".
- Cuando la rama de la búsqueda de una solución se detiene, tenemos la oportunidad de volver a algunas de las posiciones anteriores (Back Tracking), para que desde esta posición comencemos nuevamente a formar la rama de la búsqueda de una solución. Esta es una "propiedad" natural de los problemas no deterministas. La pregunta es cuál de los niveles anteriores debe devolverse. Este es el mismo problema abierto que la cuestión de elegir el índice de fila o elegir una posición libre en esta fila.
- Finalmente, debe notarse un problema relacionado con la velocidad del algoritmo. Sería triste si no hubiera un objetivo para crear algoritmos de ejecución rápida. En el proceso de modelado, no fue posible desarrollar un algoritmo que funcionara rápida y eficientemente en todas las áreas de la solución del problema. Tuve que desarrollar tres algoritmos. Transmiten los resultados uno a otro, como un bastón. Uno de ellos funciona muy rápido, pero groseramente, el otro, por el contrario, funciona de manera lenta pero eficiente. Cada uno de ellos trabaja en la "zona de su responsabilidad".
Inicialmente, el propósito del estudio era solo encontrar al menos alguna solución. Tenía mucho que resolver antes de que se desarrollara la primera solución. Tomó más de cuatro meses. Era posible detenerse allí, el objetivo se logró, bueno, está bien. Pero me pareció que no todas las posibilidades de una solución algorítmica a este problema estaban agotadas. Naturalmente, había un deseo de mejorar el algoritmo desarrollado para que la complejidad temporal del algoritmo fuera lineal-O (n). Cuando se encontró una solución tan lineal, hubo "un deseo más": reducir el número de casos cuando se aplicó el procedimiento Back Tracking (BT) al formar una rama de la búsqueda de la solución. Era un deseo "descarado" de transferir la tarea de no determinista a determinada condicionalmente (en la medida de lo posible). Tomó mucho tiempo, pero el objetivo se logró, por ejemplo, en el intervalo de valores del tamaño de un tablero de ajedrez n = (320, ..., 22500), el número de casos en los que el procedimiento BT nunca se ha utilizado es más del 50%. Resulta que en el 50% de los casos cuando se inicia el programa, el algoritmo "a propósito" forma una solución, nunca "tropieza". (Recordando el cuento de hadas sobre el pez dorado, me detuve en estos dos deseos ...)
Al comparar las publicaciones que pude conocer durante la investigación, llegué a la conclusión de que este problema y otros problemas de este tipo no pueden resolverse sobre la base de un enfoque matemático riguroso, es decir, solo sobre la base de definiciones, declaración de lemas y prueba de teoremas. Hay un "comentario filosófico" sobre esto en el artículo. Estoy seguro de que muchos problemas de muchos NP-Complete solo se pueden resolver sobre la base de las matemáticas algorítmicas con el uso del modelado por computadora. Tal conclusión no significa limitar las matemáticas, por el contrario, significa expandir las capacidades de las matemáticas mediante el desarrollo de métodos matemáticos algorítmicos. Para cada familia de problemas, debe utilizar su propio enfoque matemático adecuado. (¿Por qué instruir a un estudiante graduado para que resuelva un problema de la familia NP-Complete sin aplicar matemática algorítmica y modelado por computadora, si se sabe que realmente nada resultará de tal empresa)?
Cualquier algoritmo (programa) tiene una propiedad simple: ¡funciona o no! Quiero hacer un llamamiento a los miembros de nuestra comunidad de Habro que tienen una computadora con Matlab instalado en la zona de accesibilidad. Quiero pedirle que pruebe el funcionamiento del algoritmo considerado para resolver el problema de finalización de n-Queens . Esto tomará solo de 5 a 10 minutos. Para probar el algoritmo, debe seguir algunos pasos simples:
- Genere una composición aleatoria a partir de k reinas y verifique la corrección de esta composición.
- Según el algoritmo de decisión propuesto, complete esta composición para obtener una solución completa. O el programa debe decidir que esta composición no tiene solución.
- Verifique la corrección de la solución obtenida como resultado de la configuración.
No tiene que escribir ningún código para tales pruebas. Además del programa principal, preparé dos programas más en el lenguaje Matlab:

1. Generarion_k_Queens_Composition - generación de una composición aleatoria de tamaño k para un tablero de ajedrez arbitrario de tamaño nxn

2. Completion_k_Queens_Composition.m : completar una composición arbitraria hasta una decisión completa o decidir que esta composición no tiene solución ( programa principal ).

3. Validation_n_Queens_Solution.m : comprobar la corrección de la solución del problema n-Queens , o la corrección de la composición de k reinas.

Trabajan muy rapido. Por ejemplo, para un tablero de ajedrez, cuyo tamaño es de 1000 x 1000 celdas, el tiempo total que toma en promedio generar una composición arbitraria (0.0015 s.), Complete esta composición (0.0622 s.), Y verifique la corrección de la solución obtenida (0.0003 s.) no excede 0.1 segundos. (excluyendo el tiempo que lleva descargar datos o guardar los resultados)

Envíame un correo electrónico (ericgrig@gmail.com), si tienes la oportunidad de ayudar a un amigo, te enviaré de inmediato estos tres programas. Estaré agradecido con todos mis colegas que pueden probar objetivamente el algoritmo y expresar su opinión en la discusión.
Preparé el código fuente del programa, con comentarios detallados, que espero sean publicados en Habré pronto. Creo que aquellos que estén interesados en resolver problemas complejos de la familia NP-Complete encontrarán algo interesante para ellos.
Me gustaría apelar nuevamente a los miembros de la Comunidad Habr, pero por una razón diferente. Aquí, en Marsella (Francia), está en marcha la formación del equipo France Fold Group , cuyo objetivo es investigar y desarrollar algoritmos para predecir las propiedades fisicoquímicas de los compuestos de alto peso molecular. Creo que no vale la pena decir que esta es una tarea bastante difícil, con una larga historia, y que equipos serios en diferentes países están trabajando en este problema, incluido el equipo Khasabis de Deep Mind (puede ver el artículo sobre Habré (habr.com_Folding) . El objetivo es crear un equipo fuerte que no tenga miedo de resolver problemas complejos. Se distribuye la forma de organización del trabajo conjunto. Cada miembro del equipo vive en su ciudad y trabaja en el proyecto en su tiempo libre desde su trabajo principal. Necesitamos programadores e investigadores (físicos, químicos, matemáticos, biólogos) ), etc. programadores "imprudentes" de osto- (al cuadrado). Escríbame si le parece interesante, lo anterior es mi correo electrónico. Con más detalle lo puedo decir en la carta de respuesta.

El prefacio del artículo resultó ser tan largo como el artículo mismo. El formato de presentación familiar en Habré me permite expresar mis pensamientos más libremente, pero a juzgar por el tamaño, lo aproveché con bastante libertad. Quería escribir brevemente, pero "resultó como siempre".

PD: Pensé que los miembros de la Comunidad Habr estarían interesados en saber qué dificultades encontré al intentar publicar los resultados del estudio. Cuando se preparó el artículo, lo volví a formatear en formato .tex de acuerdo con los requisitos del Journal of Artificial Intelligence Research (JAIR) y lo envié allí. Solía haber publicaciones sobre un tema similar. De particular interés es el artículo C. Gent, I.-P. Jefferson y P. Nightingale (2017) (Complejidad de la finalización de n-reinas) , en el que los autores probaron que el problema en cuestión pertenece al conjunto NP-Completo y hablaron sobre las dificultades encontradas al tratar de resolver este problema. En las conclusiones, los autores escriben: "Para cualquiera que entienda las reglas del ajedrez, la Finalización n-Queens puede ser uno de los problemas NP-Completos más naturales de todos" ( Para cualquiera que entienda las reglas del ajedrez, la tarea de Finalización n-Queens puede convertirse en una las tareas NP-Complete más naturales ).

Después de 10 días, recibí un rechazo de JAIR, con la redacción: "el artículo no corresponde al formato de la revista", Ni siquiera tomó el artículo para su consideración. No esperaba tal respuesta. Pensé que si una revista publica artículos en los que los autores concluyen que es muy difícil resolver un problema dado y no proporciona ninguna solución específica, entonces el artículo que proporciona un algoritmo de solución eficaz será aceptado para su consideración. Sin embargo, los editores tenían su propia opinión sobre este asunto. (Creo que los especialistas competentes trabajan allí, y lo más probable es que hayan sido interrogados por el título "insolente" del artículo y todo lo que se describe allí. Pensamos, "lo más probable es que haya algún tipo de error y me enviaron suavemente, refiriéndome al formato ").

Tuve que elegir otra publicación científica periódica revisada por pares sobre temas relevantes. Aquí me enfrento a la dura realidad. El hecho es que aproximadamente el 80% de todas las revistas son pagadas: o tengo que pagar una cantidad decente a la revista para que el artículo esté disponible gratuitamente para todos los lectores, o necesitan dar el artículo como un regalo "en la proa", y cobrarán a todos los que quiere familiarizarse con este estudio. Y la primera y segunda opción son fundamentalmente inaceptables para mí. Me sentí bien con este método de raqueta editorial cuando intenté familiarizarme con algunas publicaciones.

La siguiente revista, que profesa el principio del libre acceso a la información, fue el SMAI Journal of Computational Mathematics . También se negaron con la misma redacción, aunque mucho más rápido, en dos días.

Luego se eligió una revista: Matemática discreta y ciencias de la computación teórica . Aquí los requisitos son simples, primero debe publicar el artículo en arXiv.org, y solo después de eso registrar el artículo para su consideración. Bien, seguiremos las reglas: presenté un artículo en arXiv.org . Me escribieron que publicarían el artículo en 8 horas. Sin embargo, esto no sucedió después de 8 horas, no después de 8 días. El artículo fue "retenido" por los mentores, y solo después de 9 días fue publicado. No hubo quejas en la forma y esencia del artículo. Creo que, como en el caso de JAIR, los mentores tenían dudas sobre la posibilidad de "hacer esto y escribir al respecto". Algún tiempo después, después de corregir errores técnicos, el artículo se actualizó y en su forma final se lanzó en la noche de Año Nuevo.

Tengo que detenerme en esto en detalle para mostrar que en la etapa de publicación de los resultados de la investigación puede haber problemas que no pueden explicarse lógicamente.

El siguiente es un artículo cuya traducción al inglés fue publicada en (arXiv.org) .

1. Introducción

Entre las diversas opciones para formular el problema de n-Queens , la tarea de finalización de n-Queens en cuestión tiene una posición especial debido a su complejidad. En su trabajo (Gent at all (2017)) demostró que el problema de finalización de n-Queens pertenece al conjunto NP-Complete ( mostró que n-Queens Completion es NP-Complete y # P-Complete ). Se supone que la solución a este problema puede abrir el camino para que podamos resolver algunos otros problemas del conjunto de NP-Complete .

El problema se formula de la siguiente manera. Hay una composición de k reinas, que se distribuyen consistentemente en un tablero de ajedrez de tamaño nxn . Es necesario demostrar que esta composición se puede completar para obtener una solución completa, y dar al menos una solución, o demostrar que dicha solución no existe. Aquí, por consistencia, nos referimos a una composición de k reinas para las cuales se cumplen tres condiciones del problema: en cada fila, cada columna, y también en las diagonales izquierda y derecha que pasan por la celda donde se encuentra la reina, no se encuentra más de una reina. El problema en esta forma fue formulado por primera vez por Nauk (1850) .

1.1 Definiciones

En lo sucesivo, denotaremos el tamaño del lado del tablero de ajedrez con el símbolo n . Una solución se llamará completa si todas las n reinas se colocan consistentemente en un tablero de ajedrez. Todas las demás soluciones, cuando el número k de reinas colocadas correctamente es menor que n , llamaremos a la composición. Llamamos a una composición de k reinas positiva si se puede completar antes de una solución completa. En consecuencia, una composición que no se puede completar hasta que una solución completa se llama negativa. Como análogo de un "tablero de ajedrez" de tamaño nxn , también consideraremos una "matriz de solución" de tamaño nxn . Como ejemplo, todos los algoritmos desarrollados para resolver el problema se presentarán en el lenguaje Matlab.

El estudio se realizó sobre la base de la simulación por computadora (simulación computacional). Para probar esta o aquella hipótesis, realizamos experimentos computacionales en un amplio rango de valores n = (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30,000, 50,000, 80,000, 10 ⁵ , 3 * 10 ⁵ , 5 * 10 ⁵ , 10 ⁶ , 3 * 10 ⁶ , 5 * 10 ⁶ , 10 ⁷ , 3 * 10 ⁷ , 5 * 10 ⁷ , 8 * 10 ⁷ , 10 ⁸ ) y, dependiendo del valor de n , se generaron muestras suficientemente grandes para el análisis. Llamamos a dicha lista una " lista base de n valores " para realizar experimentos computacionales. Todos los cálculos se realizaron en una computadora normal. En el momento del ensamblaje (principios de 2013), era una configuración bastante exitosa: CPU - Intel Core i7-3820, 3.60 GH, RAM-32.0 GB, GPU-NVIDIA Ge Forse GTX 550 Ti, Dispositivo de disco - ATA Intel SSD, SCSI, OS- Sistema operativo de 64 bits Windows 7 Professional . Llamamos a este kit simplemente: escritorio-13 .

2. Preparación de datos

El algoritmo comienza leyendo un archivo que contiene una matriz unidimensional de datos sobre la distribución de una composición arbitraria de k reinas. Se supone que los datos se preparan de la siguiente manera. Deje que haya una matriz puesta a cero Q (i) = 0, i = (1, ..., n) , donde los índices de las celdas de esta matriz corresponden a los índices de fila de la matriz de solución. Si en alguna fila arbitraria i de la matriz de solución hay una reina en la posición j , entonces se realiza la asignación Q (i) = j . Por lo tanto, el tamaño de composición k será igual al número de celdas distintas de cero de la matriz Q. (Por ejemplo, Q = (0, 0, 5, 0, 4, 0, 0, 3, 0, 0) significa que estamos considerando una composición de k = 3 reinas en la matriz n = 10 , donde las reinas se encuentran en la 3ra, 5ta y 8va líneas, respectivamente en posiciones: 5, 4, 3).

3. Algoritmo para verificar la corrección de la solución del problema n-Queens

Para la investigación, necesitamos un algoritmo que nos permita determinar la corrección de la solución del problema n-Queens en poco tiempo. Controlar la ubicación de las reinas en cada fila y cada columna es simple.La pregunta es sobre los límites diagonales. Podríamos construir un algoritmo efectivo para tal contabilidad si pudiéramos asignar cada celda de la matriz de solución a una celda determinada de un determinado vector de control que caracterizaría de manera única la influencia de las restricciones diagonales en la celda en cuestión. Luego, en función de si la celda del vector de control está libre u ocupada, se puede juzgar si la celda correspondiente de la matriz de decisión está libre o cerrada. Dicha idea fue utilizada por primera vez por Sosic y Gu (1990) para tener en cuenta y acumular el número de situaciones de conflicto entre diferentes posiciones de reinas. Utilizamos una idea similar en el algoritmo presentado a continuación, pero solo para tener en cuenta si la celda de la matriz de la solución está libre u ocupada. En la Figura 1, se muestra un ejemplo de un tablero de ajedrez.8 x 8 arriba de la cual en la parte superior hay una secuencia de 24 celdas.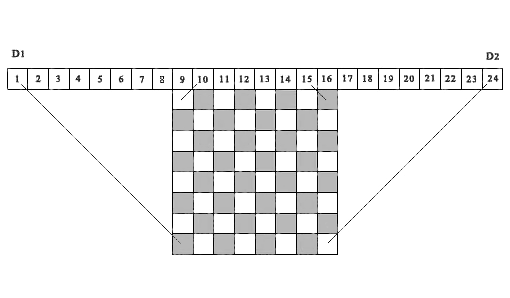

Fig.1. Un ejemplo de demostración de la correspondencia de las proyecciones diagonales de las celdas de la matriz con las celdas correspondientes de las matrices de control D1 y D2 , ( n = 8)

Considere las primeras 15 celdas como elementos del vector de control D1 . Las proyecciones de todas las diagonales izquierdas de cualquier celda de la matriz de solución caen en una de las celdas del vector de control D1 . De hecho, todas estas proyecciones se encuentran dentro de dos segmentos de línea paralelos, uno de los cuales conecta la celda de la matriz (8.1) a la primera celda del vector D1 , y el segundo conecta la celda de la matriz (1.8) a la 15a celda del vector de control D1. Damos una definición similar para las proyecciones diagonales derechas. Para hacer esto, mueva la referencia de la celda 1 a la celda 9 a la derecha, y considere la secuencia de 16 celdas como elementos del vector de control D2 (en la figura, estas son celdas del 9 al 24). Proyecciones de todas las diagonales derechas de cualquier celda de la matriz las soluciones caerán en una de las celdas de este vector de control, comenzando desde la segunda celda hasta la 16 (en la figura, del 10 al 24). Aquí, todas estas proyecciones se ubican entre dos segmentos de líneas paralelas: el segmento que conecta la celda (8,8) de la matriz de solución con la celda 16 del vector D2 (celda 24 en la figura) y el segmento que conecta la celda (1,1) de la matriz de solución con la celda 2 vectores de control D2(celda 10 en la figura). Las proyecciones de todas las celdas de la matriz de solución que se encuentran en la misma diagonal izquierda caen en la misma celda del vector de control izquierdo D1 , respectivamente, las proyecciones de todas las celdas de la matriz de solución que se encuentran en la misma diagonal derecha caen en la misma celda del vector de control derecho D2 . Por lo tanto, estos dos vectores de control D1 y D2 , permiten el control total de todas las inhibiciones diagonales para cualquier célula de la matriz de decisión.

Es importante tener en cuenta que la idea de usar proyecciones diagonales en celdas de vectores de control para determinar si una celda de una matriz de solución con coordenadas (i, j) está libre u ocupada también se implementó más tarde enRichards (1997) . Proporciona uno de los algoritmos de búsqueda recursiva más rápidos para todas las soluciones, basado en operaciones con una máscara de bits. Una diferencia importante es que el algoritmo indicado está diseñado para la búsqueda secuencial de todas las soluciones, comenzando desde la primera fila de la matriz de solución hacia abajo o desde la última fila de la matriz hacia arriba. El algoritmo que propusimos se basa en la condición de que la elección del número de cada línea para la ubicación de la reina debe ser arbitraria. Para el algoritmo en consideración, esto es de fundamental importancia. Tenga en cuenta que la figura 1 anterior, la construimos por analogía con lo que se publica en este documento.
Un programa para verificar si una solución dada del problema n-Queens es correcta, o si una composición dada de k es verdaderaQueens es como sigue.

1. Para controlar las inhibiciones diagonales, cree dos matrices D1 (1: n2) y D2 (1: n2) , donde n2 = 2 * n, y una matriz B (1: n) para controlar la ocupación de las columnas de la matriz de solución. Cero estas tres matrices.

2. Introducimos el contador del número de reinas instaladas correctamente ( totPos = 0 ). Consistentemente, en un ciclo, comenzando desde la primera línea, consideramos todas las posiciones de reinas proporcionadas. Si Q (i)> 0 , según el índice de la fila i y el índice de la posición de la reina en esta fila j = Q (i), formamos los índices correspondientes para las matrices de control D1 (r) y D2 (t) :
r = n + j - i
t = j + i

3. Si se cumplen todas las condiciones ( D1 (r) = 0, D2 (t) = 0, B (j) = 0 ), esto significará que la celda ( i, j) es libre y no cae en la zona de proyección de restricciones diagonales formadas por reinas previamente establecidas. La posición de la reina en esta posición es correcta. Si al menos una de estas condiciones no se cumple, entonces la elección de dicha posición será errónea, respectivamente, y la decisión será errónea.

4. Si la solución es correcta, incremente el contador del número de reinas instaladas correctamente ( totPos = totPos + 1 ) y cierre las celdas correspondientes de las matrices de control: (D1 (r) = 1, D2 (t) = 1, B (j) = 1) . Entonces cerramos todas las celdas en la columna(j) y aquellas celdas de la matriz de solución que se encuentran a lo largo de las diagonales izquierda y derecha que se cruzan en la celda (i, j) .

5. Repita el procedimiento de verificación para todas las posiciones restantes.
Quizás este sea uno de los algoritmos más rápidos para evaluar la corrección de la solución al problema de n-Queens . El tiempo de verificación de un millón de posiciones para la matriz de soluciones 10 ⁶ x 10 ⁶ en el escritorio-13 es de 0.175 segundos, que corresponde aproximadamente al tiempo de presionar la tecla "Enter". Obviamente, este algoritmo es lineal con respecto al recuento del tiempo con respecto a n .

4. Descripción del algoritmo para resolver el problema.

El general . El problema de finalización de n-Queens es un problema clásico no determinista. La principal dificultad de su solución está relacionada con la cuestión de elegir el índice de fila y el índice de posición en esta fila, en condiciones en las que el espacio de estado es enorme. Al buscar todas las soluciones posibles, este problema no surge. Debemos considerar todas las ramas de búsqueda válidas en el espacio de estado, y el orden en el que se consideran no importa. Sin embargo, cuando se necesita completar una composición arbitraria de k reinas hasta una solución completa, entonces en este caso necesitamos un algoritmo para seleccionar índices de fila y columna que perciba adecuadamente la composición existente y conduzca a una solución más rápida que otras. En este proyecto, la cuestión de elección la decidimos sobre la base de la siguiente posición general: si no podemos formular las condiciones que dan preferencia a cualquier fila, o cualquier posición en esta fila sobre otras, entonces usamos un algoritmo de selección aleatorio basado en números aleatorios distribuidos uniformemente . Un método de selección aleatorio similar para resolver problemas en los que el espacio de estado es enorme es bastante natural. Una de las ediciones de la serie Procedimientos de un taller DIMACS (1999) se dedicó por completo al uso de la selección aleatoria en el desarrollo de algoritmos para resolver problemas complejos. La implementación correcta del algoritmo de selección aleatoria puede ser una solución bastante productiva, aunque esta es una condición necesaria pero no suficiente para completar la solución. Sosic y Gu (1990) es uno de los primeros estudios en utilizar un algoritmo de selección aleatorio para resolver el problema n-Queens . El algoritmo que examinaron se basa en una idea bastante simple y concisa. Deje que haya una secuencia de números del 1 al n , que se reorganizan aleatoriamente. Tal conjunto de números tiene una propiedad importante. Consiste en el hecho de que no importa cómo se distribuyan estos números en diferentes filas de la matriz de solución como las posiciones de la reina (un número por línea), las dos primeras reglas siempre se cumplirán en la declaración del problema: cada fila y cada columna no tendrán Más de una reina. Sin embargo, solo una parte de las posiciones así obtenidas estará libre de restricciones diagonales. La otra parte estará en un estado de "conflicto" con reinas previamente establecidas. Para salir de esta situación, los autores utilizaron el método de comparar e intercambiar posiciones en conflicto para obtener una solución completa. En nuestro algoritmo propuesto, las situaciones de conflicto son imposibles, ya que en cada paso de resolver el problema, la reina se instala en la celda de la línea en cuestión solo si la celda está libre.

4.1 Selección de un modelo para el seguimiento posterior (BT)

En el proceso de encontrar una solución a un problema, puede surgir una situación cuando una cadena secuencial de soluciones conduce a un callejón sin salida. Esta es una propiedad "genética" de los problemas no deterministas. En este caso, debe volver a uno de los pasos anteriores, restaurar el estado de la tarea de acuerdo con este nivel y comenzar nuevamente la búsqueda de una solución desde esta posición. La pregunta es cuál de los niveles anteriores debería devolverse y cuántos niveles deberían ser (por nivel, nos referimos a un cierto paso para resolver el problema con un número determinado de reinas instaladas correctamente). Obviamente, elegir un nivel de solución para volver es tan relevante como elegir un índice de fila o un índice de posición en esa fila. Por lo tanto, independientemente del enfoque para resolver este problema, es necesario determinar primero el número de niveles básicos para regresar, así como el mecanismo y las condiciones para regresar a uno de estos niveles. En nuestro algoritmo propuesto, dividimos la matriz de solución en tres niveles básicos. Estos son los puntos de retorno. Si, como resultado de la solución, se produce un punto muerto, entonces, dependiendo de los parámetros de la tarea, volvemos a uno de estos tres niveles básicos. El primer nivel base ( baseLevel1 ) corresponde al estado cuando se completa la verificación de datos de la composición en cuestión. Este es el comienzo del programa. Los valores de los siguientes dos niveles base ( baseLevel2 y baseLevel3 ) dependen del tamaño de la matriz n . La dependencia empírica de estos valores básicos del tamaño de la matriz de la solución se estableció sobre la base de una gran cantidad de experimentos computacionales. Para una representación más precisa de esta dependencia, dividimos todo el intervalo considerado de 7 a 10 ⁸ en dos partes. Sea u = log (n) , entonces si n <30 000 , entonces

baseLevel2 = n - round (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
baseLevel3 = n - round (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

de lo contrario

baseLevel2 = n - round (-0.886344 * u3 + 56.136743 * u2 + 146.486415 * u + 227.967782)
baseLevel3 = n - round (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 Estructura de bloque

El algoritmo se construye en forma de una secuencia de cinco bloques de eventos , donde cada evento está asociado con la ejecución de una determinada parte de la solución del problema. Los algoritmos de procesamiento en cada bloque son diferentes entre sí. Solo tres de los cinco bloques sirven para formar una cadena secuencial de soluciones, y los dos bloques restantes son preparatorios. La elección del número de bloque a partir del cual comienzan los cálculos depende del valor de n y de los resultados de comparar el tamaño de composición k con los valores de baseLeve2 y baseLevel3 . Una excepción es el intervalo de valores n = (7, ..., 99) , que se puede llamar una "zona turbulenta" debido a las peculiaridades del comportamiento del algoritmo en esta sección. Para los valores n = (7, ..., 49) , independientemente del tamaño de la composición, después de ingresar y monitorear los datos, los cálculos comienzan desde el 4to bloque. Para valores n = (50, ..., 99) , dependiendo del tamaño de la composición, los cálculos comienzan desde el segundo bloque o desde el cuarto. Como se mencionó anteriormente, en cada paso para resolver el problema, solo se consideran aquellas posiciones en la línea que no entran en la zona de restricciones creadas por las reinas previamente establecidas. Son estas posiciones las que se llaman libres .
Describamos brevemente qué cálculos se realizan en cada uno de estos cinco bloques del programa.

4.3 Comienzo del algoritmo

Se ingresan los datos y se verifica que la composición sea correcta. En cada paso de verificación, se cambian las celdas de las matrices de control. Se cuenta el número de reinas instaladas correctamente. Si no hay errores en la composición, la solución continúa; de lo contrario, se muestra un mensaje de error. Una vez completada la verificación, se crean copias de las matrices principales para su reutilización en este nivel. Después de eso, el control se transfiere al Bloque-1 .

4.4 Bloque 1

El comienzo de la formación de la rama de búsqueda. Consideramos k reinas ubicadas en un tablero de ajedrez como una posición inicial. Se requiere continuar para completar esta composición y colocar las reinas en un tablero de ajedrez hasta que su número total sea igual a baseLevel2 . El algoritmo utilizado aquí se llama randSet y randSet . Esto se debe al hecho de que aquí estamos constantemente comparando dos listas aleatorias de índices, en busca de pares libres de las restricciones diagonales correspondientes. Para hacer esto, se realizan las siguientes acciones:

a) se forman dos listas: una lista de índices de filas libres y una lista de índices de columnas libres;

b) reorganización aleatoria de números en cada una de estas listas;

c) en un bucle, cada par de valores sucesivos (i, j) , donde el índice (i) se selecciona de la lista de índices de fila libre e índice (j) de la lista de índices de columna libre, se considera como una posible posición de reina y se verifica si esto posición en el área de proyección de excepciones diagonales.

Si no se viola la regla de las excepciones diagonales, la posición se considera correcta y la reina se coloca en esta posición. Después de eso, el contador se incrementa para el número de reinas instaladas correctamente, y se cambian las celdas correspondientes de las matrices de control. Si la posición (i, j) cae dentro de la zona de restricciones diagonales formadas por las reinas establecidas anteriormente, entonces nada cambia y tiene lugar la transición a la consideración del siguiente par de valores.

Cuando se completa el ciclo de comparación de todos los pares de la lista, entonces, en base a los índices restantes que están en la zona de exclusión diagonal, se forma nuevamente una lista de índices de las filas y columnas libres restantes, y este procedimiento se repite hasta el número total de reinas colocadas correctamente (totPos ) no será igual o superior al valor límite de baseLevel2 . Una vez que se cumple esta condición, el control se transfiere al Bloque-2 . Si resulta que como resultado de una búsqueda de una solución, surgió una situación de que de la lista completa de índices de las filas y columnas libres restantes, ninguno de los pares es adecuado para la ubicación de la reina, entonces, en este caso, los valores originales de las matrices de control se restauran en base a copias generadas previamente , y el control se transfiere al comienzo del Bloque-1 para volver a contar.

4.5 Bloque 2

Este bloque sirve como una etapa preparatoria para la transición al Bloque-3 . En este nivel, el número de líneas libres restantes ( freeRows ) es significativamente menor que n . Esto le permite transferir eventos desde la matriz original de tamaño nxn a una matriz de tamaño más pequeño L (1: freeRows, 1: freeRows) . Además, según la información sobre las filas y columnas libres restantes en la matriz de solución original, los ceros se escriben en las celdas correspondientes de la matriz L , lo que indica que estas celdas están libres. Con esta transición de "proyección" , se preserva la correspondencia de los índices de fila y columna de la nueva matriz con los índices correspondientes de la matriz original. Es importante tener en cuenta que, aunque, en el proceso de resolución de este problema, todos los eventos se desarrollan en la matriz original de tamaño nxn , y dicha matriz es el escenario principal de acción, en realidad esta matriz no se crea , y solo controla matrices de contabilidad para los índices de fila A (1: n) y columnas B (1: n) de esta matriz.

Junto con la matriz L, dos matrices de trabajo rAr (1: freeRows) y tAr (1: freeRows) también se forman en este bloque para guardar los índices correspondientes de las matrices de control D1 y D2 . Esto se debe al hecho de que cuando instalamos la siguiente reina en la celda (i, j) de la matriz inicial de tamaño nxn , luego debemos excluir las celdas de la matriz L que caen en la zona de proyección de las excepciones diagonales de la matriz "grande" original. Dado que el control de las restricciones diagonales se lleva a cabo solo dentro de la matriz original de tamaño nxn , la presencia de matrices de trabajo rAr y tAr nos permite mantener la correspondencia y traducir las celdas prohibidas a los límites de la matriz L. Esto simplifica enormemente la contabilidad de las posiciones excluidas.
Después de completar el trabajo preparatorio en este bloque, se crean copias de las matrices principales para su reutilización a este nivel, y el control se transfiere al Bloque-3 .

4.6 Bloque 3

En este bloque, la formación de la rama de búsqueda de solución continúa sobre la base de los datos preparados en el bloque anterior. El número de líneas en las que las reinas se establecen correctamente es igual o mayor que baseLevel-2 . Debe continuar seleccionando hasta que el número de reinas instaladas sea igual a baseLevel-3 . Aquí usamos el algoritmo de búsqueda de soluciones rand y rand , es decir Para formar la posición de una reina, en lugar de una lista de índices libres, solo se utilizan dos índices, un valor de índice aleatorio de una fila libre y un valor de índice aleatorio de una posición libre en esta fila. Este procedimiento se repite cíclicamente hasta que el número total de reinas colocadas sea igual al valor de baseLevel-3 . Tan pronto como se cumpla esta condición, el control se transfiere al Bloque-4 . Si, como resultado de los cálculos, la rama de búsqueda resulta ser un callejón sin salida, entonces esta sección de la formación de la rama de búsqueda se cierra y vuelve al comienzo del Bloque-3 , desde donde se repiten los cálculos nuevamente. Para esto, se restauran los valores iniciales de todas las matrices de control.

4.7 Bloque 4

En este bloque, los datos se preparan para la transferencia de control al Bloque-5 . Para este paso, después de completar el procedimiento en el Bloque-3 , el número de líneas libres ( nRow ) se ha vuelto aún menor. Por lo tanto, también es beneficioso traducir eventos de una matriz más grande a una matriz más pequeña. Este enfoque nos da la oportunidad de determinar rápidamente las características necesarias para las líneas restantes que necesitamos en esta etapa. De particular importancia es el hecho de que, sobre la base de dicha matriz, es posible predecir las perspectivas de la rama de búsqueda para muchos pasos hacia adelante sin tener que completar los cálculos. La condición es bastante simple. Si resulta que entre las líneas libres restantes hay una línea en la que no hay una posición libre, entonces la rama de búsqueda en consideración se cierra y el control se transfiere a uno de los bloques de nivel inferior. Las acciones preparatorias llevadas a cabo aquí son muy similares a lo que se hizo en el Bloque-2 . En base a los índices originales de filas y columnas libres, se forma una nueva matriz bidimensional, cuyos valores cero corresponden a posiciones libres en la matriz de solución original. Además, se crea una matriz especial E (1: nRow, 1: nRow) en este bloque, en función de la cual puede determinar el número de posiciones libres en las líneas libres restantes que se cerrarán si selecciona la posición (i, j) para establecer la reina en matriz fuente. Antes de transferir el control al Bloque 5 , se realizan las siguientes acciones:

a) se determina la cantidad de puestos vacantes en todas las líneas restantes,

b) una matriz de la cantidad de posiciones libres, para las filas en cuestión, se ordena en orden ascendente,

c) si todas las líneas libres restantes tienen posiciones libres (es decir, el valor mínimo en esta lista clasificada es diferente de 0), entonces el control se transfiere al Bloque-5.

Si resulta que en cualquiera de las líneas restantes no hay una posición libre, los arreglos necesarios se restauran en función de las copias almacenadas y, según los parámetros de la tarea, el control se transfiere a uno de los niveles básicos.

d) se forman copias de seguridad de todas las matrices de control para este 4to nivel.

4.8 Bloque 5

Esta etapa es final, y aquí, la formación de la rama de búsqueda se realiza más "equilibrada" y "racional". Esta es la "última milla", solo queda un pequeño número de líneas libres. Pero al mismo tiempo, esta es la parte más difícil. Todos los errores que podrían haberse cometido en las etapas anteriores de la formación de la rama de la búsqueda de una solución, en conjunto, aparecen aquí, en forma de falta de posición libre en la línea.

El algoritmo de este bloque se ejecuta sobre la base de dos bucles anidados, dentro de los cuales se ejecuta el tercer bucle. Una característica del tercer ciclo es que puede repetirse, sin cambiar los parámetros de dos ciclos externos. Esto sucede si la rama de búsqueda generada está bloqueada. El número de tales repeticiones no excede el valor límite de repeatBound , cuyo valor óptimo se estableció sobre la base de experimentos computacionales.

El índice del bucle externo está asociado con una elección secuencial de índices de fila que permanecieron libres después de los cálculos en el tercer nivel de base. Esto se realiza sobre la base de una lista de filas clasificada previamente por la cantidad de posiciones libres en la fila. La selección comienza con una línea, con un número mínimo de posiciones libres y luego, en pasos posteriores, en orden ascendente. Dentro de este ciclo, se forma un segundo ciclo, cuyo índice itera sobre los índices de todas las posiciones libres en la fila en cuestión. El propósito del primer ciclo es solo seleccionar el índice de una de las líneas libres en este nivel. En consecuencia, el propósito del segundo ciclo es solo seleccionar una posición libre dentro de la línea considerada. Estas acciones ocurren solo en el tercer nivel básico. Después de esta elección, se incrementa el número de reinas instaladas y se cambian las celdas correspondientes de todas las matrices de control. Además, el control se transfiere dentro de un ciclo anidado (tercero), cuya zona de actividad ya es todas las líneas libres restantes. Dentro de este ciclo, la elección del índice de fila y la elección de una posición libre en esta fila se realizan según las siguientes reglas:

a) Seleccione una línea libre . Se consideran todas las líneas libres restantes y se determina el número de posiciones libres en cada línea. Se selecciona la fila para la cual el número de posiciones libres es mínimo. Esto minimiza los riesgos asociados con la posibilidad de excluir los últimos puestos vacantes en algunas de las líneas restantes en las que el estado es mínimo y crítico en términos del número de puestos vacantes ( regla de riesgo mínimo ). Por cierto, es con esta regla en mente que el índice del primer ciclo en este quinto bloque comienza con una selección secuencial de filas con un valor mínimo del número de posiciones libres en una fila. Si en algún momento resulta que las dos líneas tienen el mismo número mínimo de posiciones libres, entonces el índice de una de las dos posiciones enumeradas primero en la lista clasificada se selecciona aleatoriamente. Si el número de filas que tienen el mismo número mínimo de posiciones libres es más de dos, entonces el índice de una de las tres posiciones enumeradas primero en la lista clasificada se selecciona aleatoriamente.

b) Selección de una posición libre en una fila .De la lista de todas las posiciones libres en la línea en cuestión, se selecciona una que causa un daño mínimo a las posiciones libres en todas las líneas restantes. Esto se hace sobre la base de la matriz E generada previamente. Por "daño mínimo", nos referimos a la elección de dicha posición en una línea dada que excluye la menor cantidad de posiciones libres en todas las líneas restantes (la regla de daño mínimo) Si resulta que dos o más posiciones libres en una fila tienen los mismos valores mínimos de acuerdo con el criterio de daño, entonces el índice de una de las dos posiciones enumeradas primero en la lista se selecciona al azar. Elegir una posición que excluya el número mínimo de posiciones libres en las líneas restantes minimiza el "daño" asociado con la posición de la reina en esta posición. El uso de ambas reglas permite un uso más racional de los recursos en cada paso de la formación de una rama de búsqueda. Esto reduce en gran medida los riesgos y aumenta la probabilidad de elegir una composición arbitraria para una solución completa si la composición en cuestión tiene una solución. Si en algún momento de la solución resulta que en una de las líneas restantes para consideración no hay puestos vacantes, entonces esta rama de búsqueda está cerrada. En este casoEn función de las copias de seguridad, se restauran todas las matrices de control y, si el contador de repeticiones no supera el valor límiterepeatBound, luego, sin cambiar los índices del primer y segundo ciclos externos, el trabajo del tercer ciclo anidado se repite nuevamente. Esto se debe al hecho de que en los casos en que los valores mínimos de los criterios relevantes coincidieron, hicimos una selección aleatoria. Volver a formar la rama de búsqueda en las mismas condiciones del nivel básico permite un uso más eficiente de los "recursos iniciales" proporcionados en este nivel. El número de inicios repetidos del tercer ciclo anidado es limitado, y si se excede el valor límite, la operación de este ciclo se interrumpe. Después de eso, los valores de las matrices de control se restauran y el control se transfiere al ciclo del tercer nivel de base para pasar al siguiente valor de índice. Este procedimiento se repite cíclicamente hasta que se obtiene una solución completa, o resulta queque usamos todas las líneas libres y todas las posiciones libres en estas líneas en este nivel básico. En este caso, dependiendo del número total de cálculos repetidos en varios niveles básicos, y teniendo en cuenta el tamaño de la matriz de decisión y el tamaño de la composición, uno vuelve a uno de los niveles más bajos para los cálculos repetidos, o se juzga que la composición en cuestión no puede ser Equipado para completar la solución. En el programa, para limitar el tiempo total de la factura, se acepta que el procedimientoo se juzga que la composición en cuestión no puede completarse hasta una decisión completa. En el programa, para limitar el tiempo total de la factura, se acepta que el procedimientoo se juzga que la composición en cuestión no puede completarse hasta una decisión completa. En el programa, para limitar el tiempo total de la factura, se acepta que el procedimientoEl seguimiento hacia atrás , independientemente de a qué niveles anteriores se realice el retorno, no se puede realizar más que totSimBound veces. Este valor límite se selecciona en base a experimentos computacionales para varios valores de n.

5. Análisis de la efectividad de los algoritmos de selección.

La eficiencia del algoritmo randSet & randSet . Para analizar las capacidades de este algoritmo, se llevó a cabo un experimento computacional, que consistió en colocar reinas en la matriz de la solución basada en el modelo randSet y randSet , siempre que exista esta posibilidad. Tan pronto como la rama de búsqueda llegó a un punto muerto, o se obtuvo una solución completa, el tamaño de la composición, el tiempo de la solución se fijaron y la prueba se repitió nuevamente. Se llevaron a cabo experimentos computacionales para toda la lista base de n valores . El número de pruebas repetidas para los valores n = (30, 40, ..., 90, 100, 200, 300, 500, 800, 1000) fue igual a un millón , para los valores restantes, el número de pruebas, con un aumento de n, disminuyó gradualmente de 100000 a 100. Un análisis de los resultados de los experimentos computacionales nos permite sacar las siguientes conclusiones:

a) Como resultado del primer ciclo del procedimiento randSet y randSet, en promedio, alrededor del 60% de todas las reinas están colocadas correctamente. Para n = 100, el número de reinas colocadas correctamente es 60.05%. Con un aumento en el valor de n, este valor disminuye gradualmente, y para n = 10 ⁷ asciende al 59,97%.

b) El histograma de la distribución de los valores de longitud de las composiciones obtenidas tiene la misma forma, independientemente del tamaño de la matriz de decisión n. Además, todos tienen un rasgo característico: el lado izquierdo de la distribución (al valor modal) difiere del lado derecho. La Figura 2, como ejemplo, muestra el histograma correspondiente para

Fig.2. Un histograma de la distribución de soluciones de varias longitudes para el modelo randSet y randSet ( n = 100, tamaño de muestra = 10 ⁶ ).

n = 100. Parece que el histograma se recopila de la distribución de frecuencia de dos eventos diferentes, ya que la frecuencia de ocurrencia de eventos en las partes izquierda y derecha de la distribución es diferente. Para describir esta distribución, lo más probable es que sea adecuado usar dos funciones de la densidad de la distribución normal, una de las cuales cubre el intervalo al valor modal, la otra, el intervalo después del valor modal.

c) El valor promedio del número de reinas ( qMean ) que se puede establecer en la matriz de decisión basada en este algoritmo aumenta con n. Como se puede ver en la Figura 3, donde se presenta un gráfico de la dependencia de la relación qMean / n del tamaño de la matriz n , esta relación aumenta con un aumento en el tamaño de la matriz. Por ejemplo

Fig.3. La dependencia de la relación qMean / n del valor de n para varios tamaños de la matriz de solución. El modelo es randSet & randSet , qMean es el valor promedio de la longitud de la solución.

si para una matriz de 100x100 el algoritmo de selección de posición randSet & randSet permite "sin parar" colocar reinas en un promedio de 89 líneas, entonces para una matriz de 1000x1000 , el número de tales filas aumenta en promedio a 967.

d) Basado en el algoritmo randSet & randSet, puede obtener el algoritmo completo Sin embargo, una solución es que la "productividad" de este enfoque es extremadamente baja. Como se puede ver en la Figura 4, para

Fig.4. La disminución en la probabilidad de obtener una solución completa en el modelo randSet y randSet con un aumento en n .

valores de n = 7, la probabilidad de obtener una solución completa es 0.057 . Además, con un aumento en n, la probabilidad de obtener una solución completa disminuye rápidamente, acercándose asintóticamente a cero. A partir del valor n = 48, la probabilidad de obtener una solución completa es del orden de 10 ^-6 . Después del valor umbral n = 70, para los valores subsiguientes de n, no se obtuvo una sola solución completa (con un número de pruebas igual a un millón ).

e) ModelorandSet y randSet forman ramas de búsqueda a una velocidad muy alta. Para n = 1000, el tiempo promedio para obtener la composición es 0.0015 segundos. La duración promedio de las composiciones es 967. En consecuencia, para n = 10 ^{6 el} tiempo promedio es 2.6754 segundos con una duración promedio de composiciones de 999793.

f) Excepto por un pequeño intervalo n <= 70, cuando el modelo randSet & randSet en casos muy raros puede conducir a solución completa, en todos los demás casos, la rama de decisión termina con la formación de una composición negativa, que no puede completarse hasta una solución completa. Entonces el algoritmo randSet y randSetTiene una ventaja importante: la alta velocidad de formación de la rama de búsqueda, y un inconveniente importante es que si el tamaño de la composición excede un cierto valor umbral, este algoritmo conduce a la formación de composiciones que no pueden completarse hasta una solución completa. Para superar este inconveniente, detenemos la formación de la rama de búsqueda cuando se alcanza el umbral baseLevel-2 .

La eficiencia del algoritmo rand & rand . Para determinar las capacidades del algoritmo rand & rand , se realizó una simulación computarizada bastante detallada para una lista básica de n valores . Al igual que con el modelo randSet y randSet, el número de nuevas pruebas en la mayoría de los casos fue igual a un millón . Para otros valores, el número de pruebas disminuyó gradualmente de 100,000 a 100.

Ambos algoritmos se basan en el principio de selección aleatoria. Por lo tanto, debe esperarse que las conclusiones extraídas aquí sean básicamente idénticas a las conclusiones formuladas para el modelo randSet y randSet . Sin embargo, existe una diferencia fundamental entre ellos, y consiste en lo siguiente:

a) el modelo rand & rand no funciona tan "duro" como el modelo randSet & randSet . Si hablamos de algún "índice de uso racional de las oportunidades proporcionadas", el modelo rand & randen cada paso usa los recursos de manera más racional. Esto lleva al hecho de que, por ejemplo, en n = 30, la probabilidad de obtener una solución completa de 0.00170 en este modelo es 15 veces mayor que el valor similar de 0.00011 para el modelo randSet & randSet . Además, aquí, hasta el valor umbral n = 370, permanece la probabilidad de obtener al menos una solución completa durante un millón de pruebas. Después de este valor umbral, para valores subsiguientes de n con un número de pruebas igual a un millón, no se obtuvo una solución completa sobre la base del modelo rand & rand .

b) este algoritmo es mucho más lento que el algoritmo randSet & randSet . Si paran = 1000 para generar una composición de tamaño 967, el tiempo promedio para obtener una composición será 0.0497 segundos, que es 33 más que el valor correspondiente de 0.0015 para el modelo randSet & randSet .

La razón de las diferencias entre dos métodos esencialmente similares de selección aleatoria se debe al hecho de que en el modelo randSet y randSet , para acelerar los cálculos, la selección aleatoria de la lista restante no se lleva a cabo en cada paso. En cambio, un par de índices se selecciona secuencialmente de dos listas, cuyos elementos se reorganizaron aleatoriamente. Dicha selección no es aleatoria en toda su extensión, sin embargo, se adapta bien a la lógica del problema y le permite contar rápidamente.

Para demostrar visualmente el funcionamiento del algoritmo rand & rand, se realizó el siguiente experimento:

a) Para un tablero de ajedrez de tamaño 100x100, después de cada paso de la ubicación de la reina en cualquier línea, se determinó el número de posiciones libres en cada una de las líneas libres restantes. Por lo tanto, después de cada paso de resolver el problema, recibimos una lista de líneas libres y una lista correspondiente del número de posiciones libres en estas líneas. Esto permitió construir un gráfico donde los índices de las columnas de la matriz en cuestión se trazan a lo largo del eje de abscisas, y el número de posiciones libres restantes a lo largo del eje de ordenadas. A modo de comparación, los cálculos también se llevaron a cabo para el modelo de selección secuencial de posiciones. Por selección secuencial se entiende lo siguiente. Se considera la primera línea, en la que se selecciona la primera posición libre en la lista. Luego, se considera la segunda línea, en la que también se selecciona la primera posición libre en la lista, etc. En las figuras 5 y 6.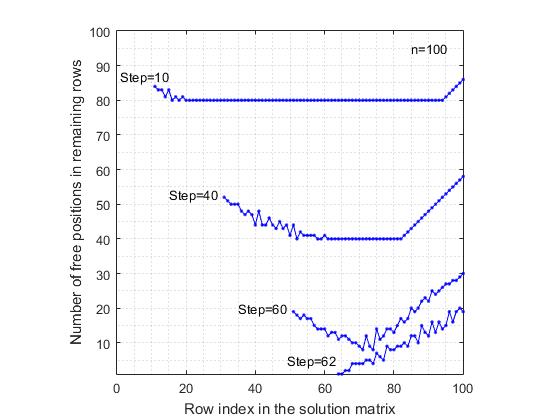

Fig.5. Reducir el número de posiciones libres en las líneas libres restantes después de la colocación de reinas. Selección secuencialmente regular de puestos.

Se presentan los resultados que corresponden a los modelos considerados. Para mayor claridad, el gráfico muestra los resultados solo después de los pasos (10, 40, 60). Para el modelo de selección secuencial de posiciones, el último es el gráfico después del paso 62, ya que la rama de búsqueda se rompe debido a la falta de una posición libre en la fila 63. Por otro lado, en el modelo rand & rand , el último gráfico se presenta después del paso 70 de colocar a la reina, aunque aquí, el número promedio de reinas colocadas correctamente alcanza 89, que es 26 pasos más que en el modelo secuencial. Una vista extraña de los gráficos en el modelo rand & randdebido al hecho de que el índice de la fila se selecciona aleatoriamente entre las filas libres restantes y, por lo tanto, se dispersan aleatoriamente por la matriz de la solución. Una comparación de estas dos figuras muestra que en el modelo secuencial de selección de posición, el rango de variabilidad del número de posiciones libres es mayor que en el modelo rand & rand . Esto se debe al hecho de que con la selección regular, las restricciones diagonales excluyen de manera no uniforme las posiciones libres en las filas restantes, lo que lleva al hecho de que en algunas filas la tasa de reducción en el número de posiciones vacantes es mayor que en otras filas.

Fig.6. Reducir el número de posiciones libres en las líneas libres restantes después de la colocación de reinas. El modelo de posicionamiento es rand y rand .

En contraste, con la selección aleatoria del índice de fila libre y el índice de columna libre, las posiciones de la reina se distribuyen uniformemente sobre el "área" de la matriz de decisión, lo que reduce la tasa de reducción "promedio" en el número de posiciones libres en las filas restantes. Por lo tanto, teniendo en cuenta las capacidades del algoritmo rand & rand , lo usamos en el programa para continuar la formación de la rama de búsqueda de soluciones hasta alcanzar el nivel baseLevel-3 .

Cabe señalar que incluso si los algoritmos de selección ( randSet & randSet, rand & rand) no sería tan efectivo, aún tendríamos que usar algún otro método de selección aleatoria al desarrollar el algoritmo. Esto se debe a la misma declaración del problema de finalización de n-Queens . Si imaginamos que existe un cierto algoritmo óptimo que resuelve el problema, entonces, en la entrada, dicho algoritmo siempre recibirá un cierto conjunto aleatorio de índices de fila y columna. Cada vez será un nuevo conjunto aleatorio de índices de fila y columna de una gran variedad de posibilidades. Para poder "asimilar" el algoritmo con una variedad de composiciones aleatorias, el algoritmo mismo debe construirse sobre la base de una selección aleatoria. La coincidencia debe ser como una llave para la cerradura . Si construimos el algoritmo sobre este principio, entonces cualquier composición consistente dek reinas serán consideradas como la posición inicial (de inicio) en el ciclo de búsqueda de decisiones. Y además, el objetivo solo será continuar la formación de la rama de la búsqueda de una solución hasta que se encuentre una solución para una composición determinada, o se demuestre que dicha solución no existe.

6. Un ejemplo de uso de la regla de riesgo mínimo (n = 100)

En la etapa inicial de encontrar una solución, cuando el número de posiciones libres en las filas no es crítico, entonces la elección del índice de la fila libre, o el índice de la posición en esta fila, no es fatal. Sin embargo, en la última etapa, cuando el número de posiciones libres en algunas filas es 1 o 2, en este caso, debe elegir un algoritmo de selección diferente. En este nivel, los algoritmos de selección aleatoria randSet & randSet y rand & rand ya no funcionarán.

El siguiente ejemplo simple explica por qué los algoritmos de selección aleatoria no funcionarán. Deje en algún paso de resolver el problema, para un valor arbitrario de n, en las filas restantes i ₁ , i ₂ , ..., i _kEl número de vacantes (indicado entre paréntesis) es: i ₁ (1), i ₂ (2), i ₃ (4), i ₄ (5), i ₅ (3), i ₆ (4) , etc. Si selecciona al azar cualquier fila, pero no la fila i ₁ , en la que solo hay una posición libre, esto puede conducir a una situación de riesgo cuando las prohibiciones diagonales relacionadas con la posición de la reina en la fila seleccionada pueden conducir al cierre de la única posición libre en la fila i ₁ , lo que llevará a la solución a un punto muerto. De todas las filas i ₁ , i ₂ , ..., i _kel más vulnerable y sensible a la elección del índice de fila es la fila i ₁ . En tales situaciones, primero debe seleccionar la fila cuyo estado es el más crítico y crea un riesgo para resolver el problema. Por lo tanto, en la última etapa de resolución del problema, en cada paso es necesario elegir la posición de la línea en función de un algoritmo simple de riesgo mínimo.

Para mayor claridad, consideremos, como ejemplo, para una matriz de 100 x 100 , la última etapa en la formación de alguna solución real, después del paso 88. Hasta que se completó la tarea, quedaron 12 líneas libres, para cada una de las cuales se encontró el número de puestos libres (las líneas se clasifican en orden creciente según el número de puestos libres):Paso-89-25 (1), 12 (2), 22 (2), 82 (2), 88 (2), 7 (3), 64 (3), 3 (4), 76 (4), 91 (4), 4 (5), 96 (5) - indica el índice de una línea libre, y entre paréntesis - el número de posiciones libres en esta línea. De acuerdo con la regla de riesgo mínimo, en el paso 89 de resolver el problema, se selecciona la fila 25 y esa posición libre que está en ella. Como resultado del recuento, nos quedan 11 líneas libres: Step-90 - 7 (2), 12 (2), 22 (2), 82 (2), 88 (2), 3 (3), 64 (3), 76 (3), 4 (4), 91 (4), 96 (4).Como puede ver, el número de posiciones libres en las primeras cinco líneas es igual e igual a 2. Por lo tanto, el índice de una de las primeras tres líneas se selecciona al azar. En este caso, se seleccionó la fila 12 y la posición de los dos restantes en esta fila, lo que conduce a un daño mínimo. Por lo tanto, en el 91º paso de la formación de la solución, tenemos 10 líneas libres: Paso 91 - 22 (1), 3 (2), 7 (2), 82 (2), 88 (2), 64 (3) 76 (3), 91 (3), 4 (4), 96 (4) . En este paso, se selecciona la línea 22 y esa posición libre que está en ella. Continuando de manera similar, se formó la siguiente secuencia de decisiones (Tabla 1). Los índices de las filas seleccionadas se muestran en negrita.

**Tabla 1. Demostración del uso de la regla de riesgo mínimo ( n = 100).**
Paso	remar	remar	remar	remar	remar	remar	remar	remar	remar	remar	remar
89	25 (1)	12 (2)	22 (2)	82 (2)	7 (3)	64 (3)	3(4)	76(4)	91(4)	4(5)	96(5)
90	7(2)	12(2)	22(2)	82(2)	3(3)	64(3)	76(3)	4(4)	91(4)	96(4)
91 91	22(1)	3(2)	7(2)	82(2)	64(3)	76(3)	91(3)	4(4)	96(4)
92	88(1)	3(2)	7(2)	82(2)	91(2)	64(3)	76(3)	4(4)	96(4)
93	3(1)	7(2)	76(2)	82(2)	91(2)	4(3)	64(3)	96(4)
94	76(1)	4(2)	7(2)	82(2)	91(2)	64(3)	96(4)
95	91(1)	7(2)	82(2)	64(3)	96(3)
96	4(1)	82(1)	7(2)	64(3)	96(3)
97	7(1)	82(1)	64(2)	96(3)
98	82(1)	64(2)	96(2)
99	64(1)	96(1)
100	64(1)

En este ejemplo particular, en 11 casos de 12, hubo una situación en la que en la lista de líneas libres restantes había al menos una línea en la que solo quedaba una posición libre. Si no utilizáramos la regla de riesgo mínimo, no podríamos llegar al final. Dado que un "movimiento incorrecto" al elegir un índice de una línea libre, probablemente conduciría a la destrucción de la única posición libre que estaba en una de las líneas libres restantes. Esta es la razón por la que cuando se usa solo el algoritmo randSet x randSet o rand x rand para obtener una solución completa, en las últimas etapas, la solución llega a un punto muerto.
Cabe señalar que el algoritmo de riesgo mínimo tiene un significado simple y cotidiano, y a menudo se usa en la toma de decisiones. Por ejemplo, el médico primero opera al paciente cuya condición es más crítica para la vida, de manera similar, el agricultor, durante una sequía severa, tratando de salvar el cultivo, en primer lugar regó las áreas que están en la condición más crítica ...

7. Análisis de la eficiencia del algoritmo.

Para evaluar la eficiencia del algoritmo para varios valores de n, se realizó un experimento computacional bastante largo (en términos de tiempo total). Inicialmente, se desarrolló un algoritmo bastante rápido para generar matrices de soluciones nQueens Problem para un valor arbitrario de n. Luego, en base a este programa, se formaron grandes muestras de soluciones para una lista básica de n valores. Los tamaños de las muestras obtenidas de nQueens Problema soluciones para varios valores de n, respectivamente, fueron iguales: (10) - 1000, (20, 30, ..., 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10,000) - -10000, (30000, 50000, 80000) - 5000, (105, 3 * 105) - 3000, (5 * 105, 8 * 105, 106) - 1000, (3 * 106) - 300, ( 5 * 106) - 200, (10 * 106) - 100, (30 * 106) - 50, (50 * 106) - 30, (80 * 106, 100 * 106) - 20. Aquí, entre paréntesis, se indica una lista de n valores, y un doble guión indica el tamaño de la muestra de las soluciones obtenidas.Después de eso, se formaron composiciones aleatorias de tamaño arbitrario sobre la base de cada muestra de soluciones. Por ejemplo, para cada una de 10,000 soluciones para n = 1000, se formaron 100 composiciones aleatorias de tamaño arbitrario. El resultado fue una muestra de un millón de canciones. Dado que cualquier composición de un tamaño arbitrario, formada sobre la base de una solución existente, se puede completar al menos una vez hasta obtener una solución completa, la tarea consistía en completar cada composición desde la muestra generada hasta una solución completa basada en el algoritmo de solución del problema de finalización n-Queens . Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenSe formaron composiciones aleatorias de tamaño arbitrario sobre la base de cada muestra de soluciones. Por ejemplo, para cada una de 10,000 soluciones para n = 1000, se formaron 100 composiciones aleatorias de tamaño arbitrario. El resultado fue una muestra de un millón de canciones. Dado que cualquier composición de un tamaño arbitrario, formada sobre la base de una solución existente, se puede completar al menos una vez hasta obtener una solución completa, la tarea consistía en completar cada composición desde la muestra generada hasta una solución completa basada en el algoritmo de solución del problema de finalización n-Queens . Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenSe formaron composiciones aleatorias de tamaño arbitrario sobre la base de cada muestra de soluciones. Por ejemplo, para cada una de 10,000 soluciones para n = 1000, se formaron 100 composiciones aleatorias de tamaño arbitrario. El resultado fue una muestra de un millón de canciones. Dado que cualquier composición de un tamaño arbitrario, formada sobre la base de una solución existente, se puede completar al menos una vez hasta obtener una solución completa, la tarea consistía en completar cada composición desde la muestra generada hasta una solución completa basada en el algoritmo de solución del problema de finalización n-Queens . Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenSe formaron 100 composiciones aleatorias de tamaño arbitrario. El resultado fue una muestra de un millón de canciones. Dado que cualquier composición de un tamaño arbitrario, formada sobre la base de una solución existente, se puede completar al menos una vez hasta obtener una solución completa, la tarea consistía en completar cada composición desde la muestra generada hasta una solución completa basada en el algoritmo de solución del problema de finalización n-Queens . Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenSe formaron 100 composiciones aleatorias de tamaño arbitrario. El resultado fue una muestra de un millón de canciones. Dado que cualquier composición de un tamaño arbitrario, formada sobre la base de una solución existente, se puede completar al menos una vez hasta obtener una solución completa, la tarea consistía en completar cada composición desde la muestra generada hasta una solución completa basada en el algoritmo de solución del problema de finalización n-Queens . Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenluego, la tarea consistía en completar cada composición de la muestra generada, basada en el algoritmo de solución del problema de finalización n-Queens, para obtener una solución completa. Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenluego, la tarea consistía en completar cada composición de la muestra generada, basada en el algoritmo de solución del problema de finalización n-Queens, para obtener una solución completa. Dado que en el algoritmo considerado en cada paso se verifica la colocación correcta de la reina en el tablero de ajedrez, aquí, en principio, no se puedenDecisiones positivas falsas (es decir, decisiones incorrectas que erróneamente consideramos correctas). Sin embargo, puede haber soluciones negativas falsas , en el caso de que el programa no complete ninguna composición formada en base a la solución existente hasta que la solución esté completa (aunque sabemos que todas las composiciones tienen una solución). Llevando a cabo un experimento computacional en un rango tan amplio de n valores, nos fijamos los siguientes objetivos:

a) determinar la complejidad temporal del algoritmo,

b) determinar la probabilidad de soluciones negativas falsas para varios valores de n,

c) para determinar la frecuencia con la que se utiliza el procedimiento Back Tracking para diferentes valores de n.

Los resultados de dicho experimento computacional se presentan en la tabla 2.

**2. n.**
n – ; m – ; t _mean , t _min , t _max – , ; t90 _mean – , 10% ; FalseNeg( FalseNegative) – , ; *t _row = t _mean *10 ⁶ / n* , 10 ⁶ , *nxn* .
n	m	t _mean	t90 _mean	t _min	t _max	FalseNeg	t _row
10	5000	0.001010	0.000532	0.000168	0.080673	2	1.0102
20	10 ⁵	0.003589	0.001809	0.000197	0.363096	5 5	1.7945
30	10 ⁵	0.008025	0.003793	0.000244	0.495716	10	2.6752
40	10 ⁵	0.014323	0.009127	0.000252	0.965817	7 7	3.5807
50	10 ⁵	0.005357	0.003589	0.000313	0.441711	9 9	10.7146
60 60	10 ⁵	0.005991	0.004103	0.000340	0.013738	10	9.9852
70	10 ⁵	0.006533	0.004566	0.000368	0.583897	8	9.3328
80	10 ⁵	0.006975	0.004987	0.000394	0.635676	7 7	8.7187
90	10 ⁵	0.006912	0.004763	0.000393	1.012710	4 4	7.6840
100	10 ⁵	0.007264	0.005107	0.000419	0.692387	4 4	7.2641
300	10 ⁵	0.013518	0.009496	0.000986	3.349766	3	4.5060
500	10 ⁵	0.028194	0.014554	0.001541	4.558749	2	5.6388
800	10 ⁵	0.049385	0.022735	0.002367	6.192782	1	6.1731
1000	10 ⁶	0.062157	0.027727	0.002943	8.015123	0 0	6.2156
3000	10 ⁵	0.177290	0.088507	0.008537	16.713140	0 0	5.9097
5000	10 ⁵	0.159239	0.136047	0.014224	42.181080	0 0	3.1849
10 ⁴	10 ⁵	0.321003	0.270927	0.028594	79.321174	0 0	3.2100
3*10 ⁴	10 ⁴	0.968795	0.651618	0.084936	139.28827	0 0	3.2293
5*10 ⁴	5000	1.147196	0.864045	0.143005	154.38225	0 0	2.2944
8*10 ⁴	4000	2.112079	1.215612	0.229532	204.27321	0 0	2.6401
10 ⁵	2000	2.253118	1.433197	0.290566	224.34623	0 0	2.2531
3*10 ⁵	2000	4.330649	3.181905	0.990932	340.29584	0 0	1.4435
5*10 ⁵	2000	5.985339	4.532205	1.488209	382.20016	0 0	1.1971
8*10 ⁵	2000	8.297512	6.554302	2.902425	75.87513	0 0	1.0372
10 ⁶	1000	11.376632	7.932194	2.954968	510.6265	0 0	1.1377
3*10 ⁶	400	23.138609	18.521503	10.433580	122.7597	0 0	0.7713
5*10 ⁶	300	33.103386	28.057816	14.937556	155.0890	0 0	0.6621
10*10 ⁶	200	61.444001	52.269241	31.624475	228.3087	0 0	0.6144
30*10 ⁶	50	149.71717	136.66441	84.556686	352.0534	0 0	0.4991
50*10 ⁶	40	253.86220	228.93732	105.37934	558.4629	0 0	0.5077
80*10 ⁶	30	372.29294	341.56397	250.80182	728.4806	0 0	0.4654
100*10 ⁶	20	508.43573	474.04890	354.80864	831.3753	0 0	0.5084

La conclusión general que se puede extraer sobre la base de los resultados obtenidos es la siguiente:

a) El algoritmo funciona lo suficientemente rápido. Por ejemplo, el tiempo promedio de compilación de una composición arbitraria para un tablero de ajedrez de tamaño 1000 x 1000 , obtenido sobre la base de un millón de experimentos informáticos, es 0.062157 segundos. Esto significa que si la composición tiene una solución, se encontrará inmediatamente después de presionar la tecla "Enter" . El tiempo de compilación promedio de una composición arbitraria, para todos los valores de n , en el rango de 7 a 30,000, no excede un segundo.

b) En cada muestra, hay aproximadamente el 10% de las composiciones, que requieren mucho más tiempo para completarse. Dichas composiciones forman una larga cola derecha en el histograma de distribución. Si excluimos este 10% de las composiciones y realizamos cálculos para el 90% restante de las soluciones, entonces el tiempo de cálculo ( _media t90 ) será mucho menor. Por ejemplo, para un tablero de ajedrez de 1000 x 1000 , el tiempo de conteo promedio será de 0.027727 segundos, que es 2.24 veces menos que el tiempo promedio obtenido de toda la muestra.

c) Para valores n≤800 , en la muestra de composiciones hubo aquellos que no pudieron completarse hasta una solución completa. Esto es falso negativodecisiones Dentro de los límites especificados en el programa, lo que permite que el procedimiento Back Tracking se realice hasta 1000 veces, el algoritmo no pudo completar estas composiciones. Se clasificaron erróneamente como composiciones negativas, es decir los que no tienen solución El número de tales soluciones falsas negativas es insignificante, y su participación en la muestra es inferior a 0,0001. Además, a medida que n aumenta , la proporción de soluciones negativas falsas disminuye. Para todos los valores de n > 800, en esta serie de experimentos computacionales, no hubo un solo caso de soluciones negativas falsas . Sin embargo, es obvio que si el tamaño de la muestra aumenta muchas veces, no se excluye la posibilidad de que aparezca Falso negativosoluciones, aunque la probabilidad de tal evento será muy pequeña.

La complejidad temporal del algoritmo . La Figura 7 muestra un gráfico de los cambios en el tiempo de recolección promedio de composiciones aleatorias para varios valores de n .

Fig.7. La dependencia del tiempo de selección promedio ( t ) de composiciones aleatorias en el tamaño ( n ) de la matriz de decisión.

El eje de abscisas representa el logaritmo decimal del valor de n , el eje de ordenadas representa el logaritmo, aumentado en 1000 veces, del tiempo promedio de conteo. Para mayor claridad, la figura también muestra la línea de puntos de la diagonal del cuadrante. Se puede ver que el tiempo de recolección aumenta linealmente con un aumento en n. En todo el rango de n valores de 50 a 10 ^{8, los} tiempos de conteo experimentales forman una línea recta, que con una correlación bastante alta ( R = 0.9998 ) se describe mediante la ecuación de regresión lineal

log (1000 * t) = - 0.628927 + 0.781568 * log (n)

Una ligera desviación de la tendencia general es característica solo para los valores n = (10, ... 49) , lo que se debe al hecho de que solo el quinto bloque de cálculos se usa en este rango para resolver el problema, cuyo algoritmo difiere significativamente de la operación de los algoritmos del primer y tercer bloque. En la dependencia obtenida, el coeficiente lineal ( 0.781568 ) es menor que la unidad, lo que lleva al hecho de que al aumentar n, la línea de regresión y la diagonal del cuadrante divergen. Para explicar claramente la razón de tal discrepancia en lugar del tiempo inicial, consideramos el tiempo promedio que es necesario para la ubicación de una reina en una línea, es decir. dividir el tiempo promedio de conteo entre n . Llamamos a tal indicador el tiempo reducido.. Obviamente, si el tiempo reducido no cambia con el aumento de n , entonces dicha solución será lineal ( O (n) ). Como se puede ver en la Figura 8, que muestra una gráfica del logaritmo del tiempo reducido

Fig.8 La dependencia del tiempo promedio ( _fila t ), que es necesario para que la reina se ubique en una línea arbitraria, en el tamaño ( n ) de la matriz de decisión.

( tRow ), incrementado en 10 ⁶ veces, desde el logaritmo del tamaño de la matriz de solución, en el rango de n de 50 a 10 ⁸ , el tiempo reducido disminuye al aumentar n . Si el tiempo reducido para n = 50 es 10.7146 * 10 ^-6 segundos, entonces el tiempo correspondiente para n = 10 ^{8 se} reduce 21 veces y es 0.5084 * 10 ^-6segundos Tal comportamiento del algoritmo, a primera vista, parece erróneo, ya que no hay razones objetivas por las cuales el algoritmo lo considerará más lento para valores pequeños de n que para valores grandes. Sin embargo, no hay error, y esta es una propiedad objetiva de este algoritmo. Esto se debe al hecho de que este algoritmo es una composición de tres algoritmos que operan a diferentes velocidades. Además, el número de líneas procesadas por cada uno de estos algoritmos cambia con el valor creciente de n. Es por esta razón que el tiempo de conteo aumenta en el rango inicial de valores n = (10, 20, 30, 40), ya que todos los cálculos en esta pequeña área se llevan a cabo solo en base al quinto bloque de procedimientos, que funciona de manera muy eficiente, pero no tan rápido como primer bloque de procedimientos. Por lo tanto, dado que el tiempo de conteo requerido para colocar a la reina en una línea,disminuye a medida que aumenta el tamaño del tablero de ajedrez, la complejidad temporal de este algoritmo se puede llamar decreciente - lineal.

El número de veces que se ha utilizado Back Tracking (BT) . En todos los casos de un experimento computacional, rastreamos el número de casos usando el procedimiento BT para resolver cada problema. Se realizó una suma acumulativa de todos los casos de uso de BT, independientemente de a qué nivel base se devolvió en el proceso de encontrar una solución. Esto nos dio la oportunidad de determinar, para cada muestra, la proporción de esas decisiones en las que el procedimiento BT nunca se ha utilizado. La figura 9 muestra

Fig.9. La proporción de decisiones en la muestra en la que el procedimiento Back Tracking nunca se ha utilizado en un

gráfico que muestra cómo cambia la proporción de casos de la solución sin utilizar el procedimiento BT ( Zero Back Tracking ) con n creciente . Se puede ver que en el rango de valores n = (7, ..., 100000) , el número de soluciones en las que nunca se ha utilizado el procedimiento BT supera el 35%. Además, en el rango de valores n = (320, ..., 22500) , el número de tales casos supera el 50%. Los resultados más efectivos se obtuvieron para un tablero de ajedrez con un tamaño de 5000 x 5000 , donde, en una muestra de 10,000 composiciones, se realizó "determinista" en el 61.92% de los casosresolviendo un problema no determinista , porque El procedimiento BT nunca se usó en el 61,92% de los casos. En las soluciones restantes, en el 21.87% de los casos, el procedimiento BT se usó 1 vez, en el 9.07% de los casos, 2 veces, y en el 3.77% de los casos, 3 veces. En conjunto, esto representa el 96,63% de los casos. El hecho de que después del valor n = 5000 , el número de casos de resolución del problema de configuración sin usar el procedimiento BT está disminuyendo gradualmente, está asociado con el modelo seleccionado para seleccionar los valores límite de baseLevel2 y baseLevel3 . Puede cambiar estos parámetros y lograr un aumento en el número de soluciones sin utilizar el procedimiento BT. Sin embargo, esto conducirá a un aumento en el tiempo de cálculo, ya que aumentará la participación del quinto bloque en la operación del algoritmo.

El histograma de la distribución de la selección del tiempo . En la Figura 10, para un valor de n = 1000 , se presenta un histograma de la distribución del tiempo de selección para un millón de decisiones. La vista no bastante ordinaria del histograma de distribución (que probablemente se asemeja a la silueta nocturna de edificios altos) no está asociada con un error en la selección de la longitud o el número de intervalos. Esta es una propiedad natural de este algoritmo. Entender

Fig.10. Un histograma del tiempo de compilación de composiciones de tamaños arbitrarios. ( n = 1000 ; tamaño de muestra = 1,000,000 )

por qué el histograma tiene esta forma, considere la distribución del tiempo de selección para composiciones que tienen el mismo tamaño. Para esto, como ejemplo, de la muestra inicial seleccionaremos todas las composiciones cuyo tamaño es de 800. Había 998 de tales composiciones en una muestra de un millón. La Figura 11 muestra un histograma de la distribución del tiempo de conteo para esta muestra. Se puede ver en la figura que la distribución consta de seis histogramas separados, con tamaños decrecientes.

Fig.11. Un histograma del tiempo de compilación de composiciones del mismo tamaño (k = 800). ( n = 1000 ; tamaño de muestra = 998 )

La razón por la cual el tiempo de compilación de 998 composiciones, en cada una de las cuales 800 reinas se distribuyen aleatoriamente, se "agrupa" en 6 grupos, porque se utiliza el procedimiento Back Tracking. El primer histograma de la figura, con el tamaño máximo de muestra, son aquellas soluciones de recolección donde el procedimiento BT nunca se ha utilizado. Este es un grupo de las soluciones más rápidas. El segundo histograma, que es significativamente más pequeño que el primero, son aquellas soluciones en las que el procedimiento BT se usó solo una vez. Por lo tanto, el tiempo de decisión en este grupo es un poco más largo que en el primero. En consecuencia, en el tercer grupo, el procedimiento BT se usó dos veces, en el cuarto, tres veces, etc., es decir, Las decisiones en las que el procedimiento BT se usó repetidamente se realizaron durante un tiempo más largo. Dichas soluciones forman la larga cola derecha de la distribución deseada.

Soluciones falsas negativas . Si dividimos todas las composiciones posibles para un valor arbitrario de na positivo y negativo, luego entre las composiciones positivas hay aquellas que este algoritmo puede clasificar como negativas. Esto se debe al hecho de que, dentro de los límites establecidos por los parámetros de búsqueda, el algoritmo no puede encontrar la forma correcta de completar tales composiciones. Como muestran los resultados experimentales (Tabla 2), el número de tales casos no excede 0.0001 del tamaño de la muestra, y el valor de este error disminuye al aumentar n . Además, para todos los valores de n> 800, no hubo un solo caso de solución falsa negativa . Incluso aumentar el tamaño de la muestra a un millón para n = 1000 no resultó en falso negativodecisiones El resultado nos permite formular la siguiente regla para resolver el problema: "Cualquier composición aleatoria de k reinas que se distribuya consistentemente en un tablero de ajedrez arbitrario de tamaño nxn puede completarse hasta que se haga una solución completa, o se decidirá que esta composición es negativa y no puede para ser completado La probabilidad de tomar tal decisión no excede 0.0001 . A medida que aumenta el tamaño de un tablero de ajedrez, disminuye la probabilidad de tomar decisiones erróneas. La complejidad temporal del algoritmo es lineal ".

8. Conclusiones

1. Se presenta un algoritmo que permite, en tiempo lineal, resolver el problema del conjunto completo hasta la solución completa de una composición aleatoria de k reinas, distribuidas consistentemente en un tablero de ajedrez de tamaño arbitrario nxn . Además, para cualquier composición de k reinas ( 1≤ k <n ), se proporciona una solución, si la hay, o se toma la decisión de que esta composición no se puede completar. La probabilidad de un error al tomar una decisión de este tipo no excede de 0,0001, y este valor disminuye al aumentar el tamaño de un tablero de ajedrez.

2. El funcionamiento de este algoritmo se basa en el uso de dos reglas importantes:

a) En la etapa final de resolución del problema, de todas las líneas libres restantes, se selecciona una para la cual el número de posiciones libres es mínimo ( regla de riesgo mínimo ). Esto minimiza los riesgos asociados con la posibilidad de excluir los últimos puestos vacantes en algunas de las líneas restantes.

b) De todas las posiciones vacantes en la línea en cuestión, se selecciona esa posición que causa un daño mínimo a las posiciones libres en las líneas libres restantes ( regla de daño mínimo ). Por " daño mínimo " se entiende la selección de dicha posición en una línea que excluye la menor cantidad de posiciones libres en todas las líneas libres restantes.

3. Se estableció que como resultado de la operación de este algoritmo, el tiempo promedio requerido para que la reina se coloque en una línea disminuye con un aumento en el valor de n. El tiempo promedio requerido para colocar a la reina en una línea en el caso cuando n es 10 ⁸ es 21 veces menor que el tiempo correspondiente para el caso n = 50.

4. Se encontró que en el rango de valores n = (7, ..., 100000) el número de soluciones en las que nunca se ha utilizado el procedimiento de seguimiento de Atrás supera el 35%. Además, en el rango de valores n = (320, ..., 22500) , el número de tales casos excede el 50%, lo que indica la alta eficiencia de este algoritmo.

5. Se propone un modelo para organizar el procedimiento Back Tracking ., basado en la separación de la secuencia de pasos de la decisión en los niveles básicos. Un nivel significa un cierto paso de decisión con un número determinado de reinas colocadas correctamente . Se dan fórmulas de regresión para calcular los valores del segundo y tercer nivel básico dependiendo de n .

6. Se presentan los resultados de un análisis comparativo de dos métodos de selección aleatoria, que se denominan randSet & randSet y rand & rand . Se ha encontrado que el algoritmo randSet & randSet es rápido, pero grosero. Por lo tanto, su uso es limitado cuando se alcanza el segundo nivel básico. Después de eso, se utiliza el algoritmo rand & rand ., que se realiza no tan rápido, pero coloca más eficazmente a las reinas en un tablero de ajedrez.

7. Se proporciona un algoritmo efectivo para verificar la corrección de la solución del problema n-Queens . Este programa también está diseñado para verificar la exactitud de una composición aleatoria de tamaño arbitrario. El programa funciona lo suficientemente rápido. Por ejemplo, el tiempo requerido para validar una solución que consta de 5 millones de posiciones es de 0,85 segundos.

9. Comentarios

1. Como se indicó al comienzo del artículo, los estudios se realizaron en el rango de n valores , de 7 a 100 millones. Sin embargo, el programa se probó en un rango más amplio de n valores , hasta mil millones. Es cierto que, en el último caso, el programa tuvo que adaptarse ligeramente, dado el gran tamaño de las matrices. Por lo tanto, si el tamaño de la RAM lo permite, entonces es posible realizar cálculos para valores grandes de n.

2. Los valores de los indicadores de línea de base, así como los valores límite del número de repeticiones en varios niveles, se optimizaron para resolver el problema dentro de todo el rango de investigación. Se pueden cambiar dentro de un rango más pequeño y reducir el tiempo de conteo. Es importante no aumentar la proporción de soluciones falsas negativas .

3. En este artículo, utilicé el tiempo de pulsación de la tecla Enter como una medida de tiempo para evaluar qué tan rápido funciona el algoritmo. Si el resultado aparece inmediatamente después de presionar la tecla, a nivel de percepción del usuario parece que el programa funciona "muy" rápido. No importa qué tan rápido funcione el algoritmo, el resultado no aparecerá en la pantalla hasta que se complete la clave. Por lo tanto, me pareció que una medida de tiempo tan condicional puede servir como un umbral para no comparar estrictamente la velocidad de varios algoritmos.

4. Filosófica ... Durante el estudio, se consideraron una gran cantidad de publicaciones relacionadas con la solución de problemas no deterministas. En la mayoría de los casos, se trataba de tareas en las que era necesario elegir en un gran espacio de estados bajo las condiciones de las restricciones dadas. Comparándolos, fue interesante saber hasta dónde se puede avanzar en la resolución de tales problemas utilizando el enfoque matemático estándar. Tengo la impresión de que es imposible resolver tales problemas solo sobre la base de definiciones, enunciados de lemas y pruebas de teoremas. Me parece que para resolver estos problemas es necesario utilizar los métodos de las matemáticas algorítmicas utilizando la simulación por computadora. Para demostrar la validez de esta conclusión, como un simple ejemplo, me preparé para un tablero de ajedrez cuyo tamaño es 10⁹ x 10 ⁹ dos composiciones del mismo tamaño, que consta de 999,999,482 reinas. Se preparan como se describe al principio del artículo y se presentan como dos archivos en formato .mat. Se pueden descargar en este enlace (dos archivos de prueba) . Los archivos son bastante "pesados", el tamaño de cada uno de ellos es de aproximadamente 3.97 Gb. En 999 997 976 líneas (en el 99,9998% de los casos) las posiciones de las reinas en ambas composiciones coinciden, y solo en 1506 líneas arbitrarias difieren las posiciones de las reinas.

Para completar los datos de composición en una solución completa, debe colocar correctamente las reinas en las 518 líneas libres restantes. El número de formas posibles de organizar 518 reinas en las líneas libres restantes (teniendo en cuenta solo el número de formas de seleccionar una posición libre en la línea seleccionada) es aproximadamente 10 ¹⁴⁶⁶. La diferencia entre estas dos composiciones consiste solo en el hecho de que una de ellas es positiva y puede completarse hasta una solución completa, y la otra composición es negativa; no puede completarse hasta una solución completa. Pregunta: "¿Es posible, sobre la base de un enfoque matemático riguroso (es decir, sin llevar a cabo operaciones computacionales algorítmicas), determinar cuál de estas dos composiciones es positiva?" Si esto es imposible de resolver, entonces podemos suponer que la proposición hecha se prueba por contradicción.

Quiero señalar que no importa cuál sea el enfoque para la solución estrictamente matemática de este problema, es necesario determinar el estado 518 * 10 ⁹celdas en las filas libres restantes. Para hacer esto, es necesario considerar cada posición de las reinas previamente establecidas, y hay casi mil millones de ellas, para establecer las restricciones que cada reina establecida impone a las posiciones libres en las 518 líneas restantes. No encontré un "punto de apoyo" que me permitiera hacer este trabajo solo sobre la base de un enfoque estrictamente matemático, sin cálculos algorítmicos.

He dado aquí un ejemplo mínimo que consta de solo dos composiciones. Si es necesario, se puede aumentar el número de tales composiciones.

Cabe señalar que, sobre la base del algoritmo lineal propuesto, ligeramente adaptado para trabajar con grandes composiciones, las tareas de las dos composiciones de prueba se pueden completar hasta que se realice una solución completa en el escritorio-13 , en aproximadamente 4.5 minutos (excluyendo el tiempo de carga de datos de entrada).

10. Además

La acción de los profesores que recomiendan tareas capaces de desarrollar e investigar para los estudiantes es digna de respeto. Esto requiere un esfuerzo considerable, pero al superar las dificultades, el investigador considera otras tareas complejas de manera diferente. Pensé que sería útil expandir las opciones para configurar el problema n-Queens para tales propósitos. Si observa la misma tarea desde diferentes perspectivas, puede ver diferentes cosas. A continuación se presentan algunos de ellos.

1. Considere el problema de organizar n reinas en un tablero rectangular de "ajedrez" de tamaño nxm . Denote k = m - n . Deje que se obtenga alguna solución, y en cada uno de nHabía una reina en cada fila. Excluimos aquellas posiciones donde se encuentran las reinas de mayor consideración. Ahora en cada línea hay una posición libre m-1 . Dentro de las posiciones libres restantes, nuevamente encontramos una solución. Como antes, excluimos de mayor consideración las posiciones donde se encuentran las reinas de la segunda solución. Ahora en cada fila hay posiciones libres m-2 . Obviamente, la primera y la segunda solución no se cruzan en sus posiciones en ninguna fila, son ortogonales. Se requiere determinar el número máximo de soluciones mutuamente ortogonales para varios valores de k . Si se encuentran n soluciones mutuamente ortogonales para el valor k = 0entonces se construirá la Royal Latin Square.

Nota . El papel Grigoryan E. (2018) han demostrado que para cualquier solución de n-Queens Problema hay una solución complementaria, que no interfiera con él. Esto significa que para un valor arbitrario de n , el conjunto de todas las soluciones del problema n-Queens se divide en dos subconjuntos de igual tamaño . Cualquier solución del segundo subconjunto es una solución complementaria a la solución correspondiente del primer subconjunto. La regla es bastante simple, si Q1 (i) es una solución del primer conjunto, entonces la solución complementaria correspondiente Q2 (i)a partir del segundo subconjunto está determinado por la fórmula Q2 (i) = n + 1 - Q1 (i), donde i = (1, ..., n) . Es esta regla la que explica el hecho de que el número de todas las soluciones del problema n-Queens , para un valor arbitrario de n , siempre es un número par. (Esta regla nos permite reducir a la mitad el tiempo para calcular todas las soluciones completas para un tamaño arbitrario n del tablero de ajedrez. Si denotamos por 2 * k el número total de todas las soluciones, entonces el valor k es igual al índice en la lista secuencial de todas las soluciones cuando Q (k) + Q ( k + 1) = n + 1 ).

2. En la formulación inicial del problema Problema n-Qeens , después de que la reina se coloca en posición (i, j), se realizan las siguientes acciones:

a) se excluyen todas las celdas de la fila i y la columna j

; b) se excluyen todas las celdas ubicadas en la línea de las diagonales izquierda y derecha que pasan por la celda (i, j) .

Cambiamos la condición b) en el enunciado del problema. En lugar de eliminar células, usaremos el cambio de células. Si la celda ubicada en la línea de las diagonales izquierda o derecha está libre, entonces la cerraremos; si la celda está cerrada, la abriremos. Esto hace que sea más fácil encontrar una solución. Sin embargo, en lugar de la matriz cuadrada nxn , consideramos una matriz rectangular de tamaño nx (n - k) . Se requiere, para un valor dado de n , encontrar el valor máximo de ken el que se pueden obtener al menos tres soluciones ortogonales. ¿Cómo cambiará el valor de k con el valor creciente de n ?

3. Cambie algunas condiciones en la formulación inicial del problema del problema n-Queens . Cuando la reina se coloca en la posición (i, j) en un tablero de ajedrez de tamaño nxn :

a) excluimos todas las celdas en la fila i ,

b) si el índice j es un número par, entonces:

b1) excluimos celdas en filas pares de la columna j,

b2) excluimos celdas en líneas pares que intersectan las diagonales izquierda y derecha que pasan a través de la celda (i, j) ,

c) Si el índice jnúmero impar, luego los elementos b1) y b2) se satisfacen para las celdas ubicadas en líneas impares.

3.1 Se sabe (Sloane-2016) que la lista de valores de todas las soluciones del problema nQueens , para n = (8, 9, 10, 11, 12, 13, 14, 15, 16) , respectivamente, es (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512) . ¿Cómo cambiará el número de todas las soluciones si, en el enunciado del problema, la condición estándar para las excepciones diagonales se cambia al párrafo b) o al párrafo c)?

3.2 Grigoryan (2018) sabe que si determinamos la frecuencia de participación de diferentes celdas de la matriz de solución en la formación de una lista de todas las soluciones, podemos encontrar que existen relaciones armoniosas entre todas las celdas en forma de simetrías verticales y horizontales de las frecuencias correspondientes. Esto significa que si suponemos que k <n / 2 , entonces la frecuencia de las celdas de la fila k-ésima será idéntica a las frecuencias de las celdas de la fila n-k + 1 . Del mismo modo, la frecuencia de las celdas de la columna k-ésima será idéntica a las frecuencias de las celdas de la columna n-k + 1 . Pregunta: "¿Cómo cambiarán estas relaciones armoniosas en el contexto de la tarea?"

4. Todas las celdas de un tablero de ajedrez se dividen en dos clases por su color. Se cree que un color es blanco, el otro es negro. Considere dos tableros de ajedrez y coloque uno de ellos sobre el otro para que los bordes coincidan completamente. Como resultado, obtenemos un "emparedado" de dos tableros de ajedrez, en el que coinciden la disposición de las celdas blancas y negras. La tarea es encontrar soluciones simultáneamente en dos tableros, observando las siguientes condiciones:

a) Si en uno de los tableros la reina está en una celda negra con índices (i, j) , entonces:

- en ambos tableros todas las celdas negras que ocurren en la fila i y columna j ,

- en ambos tableros se excluyen todas las celdas negras que se encuentran a lo largo de las diagonales izquierda y derecha que pasan a través de la celda (i, j) .

b) Si en una de las tablas la reina se encuentra en una celda blanca con índices (i, j) , entonces todas las acciones del párrafo a) se realizan solo para las celdas blancas.

5. Imagine que en una matriz de solución de tamaño nxn , las filas pueden deslizarse una con respecto a la otra hacia la derecha o hacia la izquierda, con un paso de k celdas. Además, si la fila anterior se desplazó, por ejemplo, a la izquierda, entonces la siguiente fila debería desplazarse a la derecha, es decir cada línea siguiente se desplaza en la dirección opuesta a la línea anterior. Como resultado de esta construcción, obtenemos una matriz rectangular de tamañonx (n + k) , donde en cada fila se excluirán de la consideración k celdas desde el principio de la línea o desde el final. La tarea es encontrar el valor máximo de k para un valor arbitrario de n para el que hay al menos una solución n-Queens Problema . Considere una variante del problema en el que el desplazamiento de una línea con respecto a otra es un número aleatorio que varía de k1 a k2 . 6. La formulación unidimensional del problema nQueens . Deje n segmentos de longitud arbitraria, numerados del 1 al n , en el medio eje . Divide cada segmento por n

celdas de tamaño arbitrario, y dentro de cada segmento, numere las celdas del 1 al n . Llamamos a tales células abiertas. Se requiere una estrecha celda uno en cada segmento, teniendo en cuenta las siguientes limitaciones:

a) podemos elegir una celda abierta con el índice j de la i ésimo segmento si:

D1 (r) = 0;

D2 (t) = 0;

donde r = n + j - i, t = j + i, D1 y D2 son matrices de control unidimensionales que consisten en 2n celdas que fueron puestas a cero previamente.

b) Después de esta elección, el segmento i y las celdas con el número j se cerraránen todos los segmentos libres restantes. También es necesario cerrar las celdas correspondientes en las matrices de control:

D1 (r) = 1;

D2 (t) = 1;

En esta configuración, la tarea es completamente idéntica a la original. De interés es la formulación de este problema con otras condiciones de restricción. Por ejemplo, si en lugar de las fórmulas:
R = n + j - i, t = j + i, ,
será considerado otras relaciones, que están asociados funcionalmente índices r y t índices (i, j) que hacen una matriz.

7. La redacción de la tarea sobre la base de una urna con bolas (idéntica a la redacción anterior). Supongamos que hay n urnas numeradas del 1 al n, y en cada urna hay n bolas, también numeradas del 1 al n . Requiere urna de distancia de cada una bola, teniendo en cuenta las siguientes limitaciones:

a) podemos seleccionar el globo con el número j de la i º urna si:

D1 (r) = 0 ,

D2 (t) = 0 ,

donde r = n + j - i, t = j + i, D1 y D2 son matrices de control unidimensionales que consisten en 2n celdas que fueron puestas a cero previamente.

b) Después de esta elección, las urnas i y las bolas con el número j se cerrarán en todas las urnas libres restantes. También es necesario cerrar las celdas correspondientes en las matrices de control:

D1 (r) = 1 ,

D2 (t) = 1 .

En esta configuración, la tarea es completamente idéntica a la original. Como en el caso anterior, el enunciado de este problema con otras condiciones que conectan funcionalmente los índices r y t con los índices (i, j) de la matriz de decisión es de interés .

8. El juego . Considere un tablero de ajedrez de tamaño nxn . Regresemos el color a las reinas, dejemos que algunas reinas tengan color blanco, otras negras. También devolvemos el color blanco y negro alternativo a las celdas del tablero de ajedrez, en función del hecho de que la celda con el índice (1, n)debería ser blanco Todas las celdas al comienzo del juego se consideran gratuitas. Las reinas blancas hacen el primer movimiento. El jugador coloca a la reina en una celda libre arbitraria con índices (i, j) . Deja que sea un glóbulo blanco. Como resultado de esta elección, se cierran:

a) todas las celdas blancas de la fila i ,

b) todas las celdas blancas de la columna j ,

c) todas las celdas blancas que se encuentran en las diagonales izquierda y derecha que pasan por la celda (i, j) .

Si la celda (i, j) resulta ser negra, entonces todos los puntos (a, b, c) están satisfechosy, en consecuencia, todas las celdas de color negro están cerradas. Luego, las negras realizan el movimiento, colocando a la reina en cualquiera de las celdas libres restantes. Después de eso, de manera similar, las células se cierran, como se describió anteriormente. El tiempo para pensar en el próximo movimiento es fijo y se selecciona por acuerdo de las partes. Si durante el tiempo especificado, uno de los jugadores no completa su movimiento, el juego se transfiere al otro. El juego termina si ambos jugadores, uno tras otro, no logran completar su turno en el tiempo especificado. El que puede colocar más reinas en el tablero gana.

9. Sobre la estabilidad de la selección aleatoria. Considere el modelo randSet y randSet . Como resultado de comparar n pares aleatorios de índices de fila y columna, en la primera etapa del ciclo, es posible establecer las reinas en promedio enk * n líneas. El valor de k puede considerarse un valor constante igual a 0.6. Su valor varía de 0.605701 en n = 10 , y a 0.599777, en n = 10 ⁶ , y, al aumentar n , la varianza de este valor disminuye. ¿Cuál es la razón de tal "constancia"? ¿Por qué, con una selección aleatoria del índice de fila y el índice de posición de la reina en esta fila, sobre la base de dos listas de números obtenidas sobre la base de una permutación aleatoria de números del 1 al n, es posible colocar consistentemente a las reinas (en promedio) en el 60% de las líneas?

10. Deje que el tamaño del tablero de ajedrez sea nxn . Basado en el procedimiento randSet y randSetcoloca a las reinas en el tablero de ajedrez hasta que la rama de búsqueda llegue a un callejón sin salida. Denote la longitud de la composición así obtenida por k . Si, para un valor dado de n, repite este procedimiento muchas veces y construye un histograma de la distribución de valores de k , entonces resulta que el cambio en la frecuencia de ocurrencia de eventos al valor del modo de distribución difiere del cambio en la frecuencia de ocurrencia de eventos después de este valor. Si, en función del valor modal, el histograma se divide en dos partes, la parte izquierda no coincidirá con la parte derecha. Este patrón es característico para cualquier valor de n. ¿Por qué, después de la transición de la duración de la composición a través del valor modal, la frecuencia del inicio de eventos toma una forma diferente? Por evento, nos referimos a recibir una composición de un tamaño determinado, antes de llegar a un estado de impasse.

Literatura

1. Nauck, F. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung, 15, 182.

2. Gent, IP, Jefferson, C. & Nightingale, P. (2017). Complejidad de la finalización de n-Queens ,
Journal of Artificial Intelligence Research., 59, 815-848.

3. Sosic, R. y Gu, J. (1990). Un algoritmo de tiempo polinómico para el problema de n-reinas . Boletín SIGART, 1 (3), 7–11.

4. Richards, M. (1997). Algoritmos de retroceso en MCPL utilizando patrones de bits y recursividad .
Tech. representante, Laboratorio de Computación, Universidad de Cambridge.

5. Métodos de aleatorización en el diseño de algoritmos , Proceedings of a DIMACS Workshop, Princeton, New Jersey, USA, December 12-14, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 43, DIMACS/AMS 1999, ISBN 978-0-8218-0916-7

6. Grigoryan E. (2018). Investigation of the Regularities in the Formation of Solutions n-Queens Problem . Modeling of Artificial Intelligence, 5(1), 3-21

7. Sloane N.-JA (2016). The on-line encyclopedia of integer sequences.

Problema de finalización de n-Queens: algoritmo de solución lineal