Campos lógicos en bases de datos, ¿hay un antídoto?

A menudo, las tablas contienen una gran cantidad de campos lógicos, no hay forma de indexarlos todos, y la efectividad de dicha indexación es baja. Sin embargo, para trabajar con expresiones lógicas arbitrarias en SQL, es adecuado un mecanismo de indexación multidimensional, que se analizará en el cat.

En SQL, los campos lógicos se utilizan principalmente en dos casos. Primero, cuando realmente necesita un atributo binario, por ejemplo, 'comprar / vender' en la tabla de transacciones. Tales atributos rara vez cambian con el tiempo.

En segundo lugar, registrar el estado de la máquina de estado que describe el registro. Se entiende que un objeto lógico que corresponde a una entrada de la tabla pasa a través de una serie de estados, cuyo número y las transiciones entre ellos están determinados por la lógica aplicada. Un ejemplo simple es la técnica de "eliminación suave", cuando un registro no se destruye físicamente, sino que solo se marca como eliminado.

Si la máquina es compleja, puede haber una buena cantidad de tales campos, en una de nuestras tablas hay 58 (+14 obsoletos) de dichos campos (incluidos los conjuntos de banderas) y esto no es algo fuera de lo común. Esto no fue pensado originalmente, pero a medida que el producto se desarrolla y los requisitos externos cambian, las máquinas correspondientes se desarrollan, los desarrolladores van y vienen, los analistas cambian ... en algún momento puede ser más seguro obtener una nueva bandera que comprender todas las complejidades. Además, los datos históricos se han acumulado y sus condiciones deben seguir siendo adecuadas.


Obtener una bandera significa no solo agregar un campo del tipo correspondiente, sino también tenerlo en cuenta en la operación del autómata, que indica que afecta, en qué transiciones participa. En la práctica, se ve así:

• un proceso o una serie de procesos, llamémoslos "escritores", cree nuevos registros en el estado inicial (posiblemente en uno de los estados iniciales)
• una serie de procesos, llamémosles "lectores", de vez en cuando leen objetos que se encuentran en los estados que necesitan
• una serie de procesos, llamémoslos "manejadores", supervise estados específicos y, según la lógica aplicada, cambiemos estos estados. Es decir operar una máquina de estados.

Para seleccionar registros que se encuentran en un estado particular, es raro que el filtrado por uno de los campos booleanos sea suficiente. Por lo general, esta es una expresión completa, a veces no trivial. Parece que necesita indexar estos campos y el procesador SQL lo resolverá. Pero no tan simple.

En primer lugar, puede haber muchos campos booleanos; indexarlos todos sería demasiado derrochador.

En segundo lugar, puede resultar inútil ya que la selectividad para cada uno de los campos será baja, y la probabilidad conjunta no está cubierta por las estadísticas del procesador SQL.

Supongamos que en la tabla T1 hay dos campos booleanos: F1 y F2, y la consulta

select F1, F2, count(1) from T1 group by F1, F2 

da

Es decir aunque, de acuerdo con F1 y F2, verdadero y falso son igualmente probables, la combinación (verdadero, falso) se cae solo una vez de cada mil. Como resultado, si indexamos F1 y F2 por separado y forzamos su uso en la consulta , el procesador SQL tendría que leer la mitad de ambos índices y cruzar los resultados. Puede ser más barato leer la tabla completa y calcular la expresión para cada línea.

E incluso si recopila estadísticas sobre solicitudes completadas, no será de mucha utilidad. Las estadísticas específicamente para los campos responsables del estado de la máquina flotan mucho. De hecho, en cualquier momento puede venir un "controlador" y transferir la mitad de las líneas del estado S1 a S2.

Para trabajar con tales expresiones, se sugiere un índice multidimensional, cuyo algoritmo se presentó anteriormente y demostró ser bastante bueno.

Pero primero debe descubrir cómo una expresión lógica arbitraria se convertirá en una consulta (s) para el índice.

Forma normal disyuntiva

Una sola consulta a un índice multidimensional es un rectángulo multidimensional que limita el espacio de consulta. Si el campo participa en la solicitud, se establece una restricción para ello. Si no, el rectángulo en esta coordenada está limitado solo por el ancho de esta coordenada. Las coordenadas lógicas tienen una capacidad de 1.

Una consulta de búsqueda en dicho índice es una cadena de & (conjunción), por ejemplo, la expresión: v1 & v2 & v3 & (! V4), equivalente a v1: [1,1], v2: [1,1], v3: [1, 1], v4: [0,0]. Y todos los demás campos tienen un rango: [0,1].

Ante esto, nuestra mirada se dirige inmediatamente al DNF , una de las formas canónicas de expresiones lógicas. Se argumenta que cualquier expresión puede representarse como una disyunción de conjunciones literarias. Un literal aquí se refiere a un campo lógico o su negación.

En otras palabras, a través de manipulaciones simples, cualquier expresión lógica puede representarse como una disyunción de varias consultas a un índice lógico multidimensional.

Hay un PERO. Tal transformación en algunos casos puede conducir a un aumento exponencial en el tamaño de la expresión. Por ejemplo, conversión de



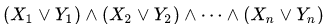
conduce a una expresión de 2 ** n términos. En tales casos, el desarrollador de la aplicación debe pensar en el significado físico de lo que está haciendo, y por parte del procesador SQL, siempre puede negarse a usar el índice lógico si el número de conjunciones excede los límites razonables.

Algoritmo de indexación multidimensional

Para la indexación multidimensional, se utilizan las propiedades de una curva de numeración autosimilar basada en símplex hipercúbicos con el lado 2. Como resultó , dos versiones de tales curvas son de importancia práctica: la curva Z y la curva de Hilbert.


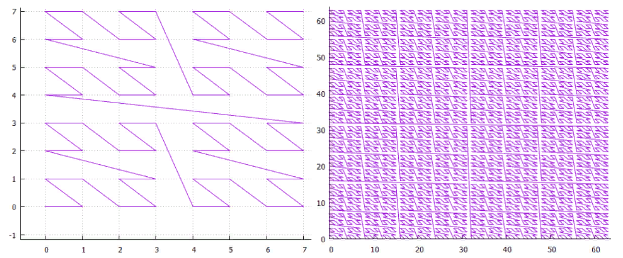Figura 1 curva Z bidimensional, 3 y 6 iteraciones


Figura 2 curva de Hilbert bidimensional, 3 y 6 iteraciones

• Un simplex N-dimensional con el lado 2 tiene 2 ** n vértices y (2 ** n-1) transiciones entre ellos.
• Una iteración elemental de un simplex convierte cada vértice de un simplex en un simplex de nivel inferior.
• Habiendo hecho la cantidad necesaria de iteraciones, podemos construir una red hipercúbica de cualquier tamaño.
• Además, cada nodo de esta red tendrá su propio número único: la ruta tomada a lo largo de la curva de numeración desde su comienzo. Además, cada nodo de esta red tiene un valor en cada una de las coordenadas. De hecho, la curva de numeración traduce el punto multidimensional en un valor unidimensional adecuado para indexar con un árbol B regular .
• Todos los nodos ubicados dentro de un simplex de cualquier nivel están dentro del mismo intervalo y este intervalo no se cruza con ningún simplex del mismo nivel.
• Por lo tanto, cualquier rectángulo de búsqueda (cuadro) se puede dividir en un pequeño número de subconsultas hipercúbicas, dentro de cada una de las cuales el índice se puede leer mediante una búsqueda / recorrido.
  
• A esto agregamos la magia del trabajo de bajo nivel con el árbol B para no hacer solicitudes inútiles y ... el algoritmo está listo.

Así es como funciona en la práctica:


Figura 3 Ejemplo de búsqueda en índice bidimensional (curva Z)

La Figura 3 muestra la división de la extensión de búsqueda original en subconsultas y los puntos encontrados. Se utilizó un índice bidimensional, construido sobre un conjunto aleatorio y uniformemente distribuido de 100,000,000 puntos en extensión [1,000,000, 1,000,000].

Índice lógico multidimensional

Ya que estamos hablando de indexación multidimensional, ¿es hora de pensar cuánto puede ser multidimensional? ¿Hay alguna limitación objetiva?

Por supuesto, debido a que el árbol B tiene una organización de página y para ser un árbol, se debe garantizar que al menos dos elementos encajen en la página. Si toma la página por 8K, almacenar un elemento no puede ir más allá de 4K. En 4K, sin compresión, se ajustan unos 1000 valores de 32 bits. Esto es bastante, más allá de los límites de cualquier aplicación razonable, podemos decir que los límites físicos prácticamente no están disponibles.

Hay otro lado, cada dimensión adicional no es gratis, ocupa espacio en disco y ralentiza el trabajo. Desde el punto de vista del "significado físico", los campos que cambian al mismo tiempo deben incluirse en el mismo índice y la búsqueda de ellos también va de la mano. No tiene sentido indexar todo en una fila.

Los campos lógicos son diferentes. Como hemos visto, docenas de campos lógicos pueden estar involucrados en los mismos mecanismos. Y los costos de almacenamiento / lectura son bastante pequeños. Existe la tentación de recopilar todos los campos lógicos en un índice y ver qué sucede.

Es cierto, hay matices:

• Hasta ahora, en el valor indexado, los dígitos de diferentes coordenadas se mezclaban, en los dígitos menos significativos de la clave eran los bits menos significativos de las coordenadas ... Por lo tanto, el orden de los campos durante la indexación no importaba.
• Ahora, se gasta un bit en almacenar el valor de un campo lógico. Es decir algunos campos lógicos irán al final de la clave y otros al principio. Esto significa que el filtrado por parte de los campos será muy efectivo, y para algunos será muy ineficiente. De hecho, si hacemos una búsqueda en el orden más bajo, tendremos que leer todo el índice para obtener una respuesta. Pero esto (muy probablemente) es mejor que leer la tabla completa para responder la misma pregunta.
• Hay un problema de elección: todos los campos lógicos son iguales, pero algunos serán más iguales que otros. Por consideraciones generales, es necesario observar las distorsiones de las estadísticas, cuanto más fuerte sea la relación verdadero / falso para un campo en particular distante del equilibrio, más antigua debería ser la descarga en la que aparece su valor.
• La división por el tipo de curva de numeración desaparece, si antes era necesario elegir entre la curva Z y la curva de Hilbert, no hay diferencia práctica en los datos de un solo bit.
• NULOS Basado en el hecho de que NULL no es un valor desconocido, sino la ausencia de cualquier valor, dichos registros no deben incluirse en el índice. En los índices unidimensionales, esto es lo que sucede. Pero en nuestro caso, puede resultar que algunos de los campos lógicos contengan valores y otros no. Como resultado, no podemos poner esto en el índice ya que El algoritmo de búsqueda no sabe cómo trabajar con lógica ternaria. Y por lo tanto, tales registros deberían ser imposibles de insertar en la tabla (si hay un índice multidimensional, no necesariamente lógico, por cierto)

Se espera que un índice multidimensional lógico en algunos casos no funcione de manera muy eficiente. Estrictamente hablando, cualquier índice puede funcionar de manera ineficiente si demasiados datos caen en el área de búsqueda. Pero para un índice multidimensional lógico, esto se ve agravado por la dependencia del orden de campo descrito anteriormente, cuando, en aras de un pequeño resultado, tiene que leer todo el índice. En la medida en que esto sea un problema en la práctica, solo el experimento puede mostrar.

Experimento numérico

Construyendo un índice:

• el índice será de 128 bits, es decir construido en 128 campos lógicos
• y contendrá 2 ** 30 elementos
• El valor del elemento índice será un número de 0 a 2 ** 30
• la clave del elemento índice será el mismo número desplazado 48 bits a la izquierda, es decir los campos lógicos 48 a 78 se completarán con los dígitos del número en el mismo orden
• Como resultado, obtenemos 30 campos lógicos significativos en el medio de la clave, los bits restantes se llenarán 0
  
• Cada uno de los campos booleanos tiene estadísticas iguales verdadero / falso
• Todos son estadísticamente independientes.

Búsqueda:

• Cada experimento corresponde a la selección de varios campos lógicos consecutivos y la asignación de valores de búsqueda para ellos. No porque el algoritmo solo pueda buscar en franjas, sino porque es posible visualizar los resultados del experimento más claramente, solo tenemos dos dimensiones: el ancho de la tira y su posición
• Un total de 24 series de experimentos. En cada serie buscaremos valores donde la tira de campos lógicos del ancho correspondiente N (de 1 a 24 bits) tome el valor verdadero.
• En cada serie habrá una subserie de experimentos en la que se ubica una franja de campos lógicos de un ancho seleccionado con diferentes cambios S desde el comienzo de la franja en 30 campos lógicos significativos. Experimentos totales (30-N) en la subserie.
• En cada experimento, se realiza una búsqueda de todos los elementos del índice que satisfacen la condición, es decir, los campos con números en el intervalo [48 + S, 48 + S + N -1] se buscarán en el intervalo [1,1], el resto en el intervalo [0,1]
  
• La búsqueda se realiza desde un inicio en frío
• El resultado es el número de páginas de disco leídas, incluido el almacenamiento en caché (caché de 4096 páginas)
• El control de la operación correcta se realiza de dos maneras: el número de elementos encontrados debe ser igual a 2 ** (30-N) y en los valores encontrados puede verificar los dígitos correspondientes
  

Entonces


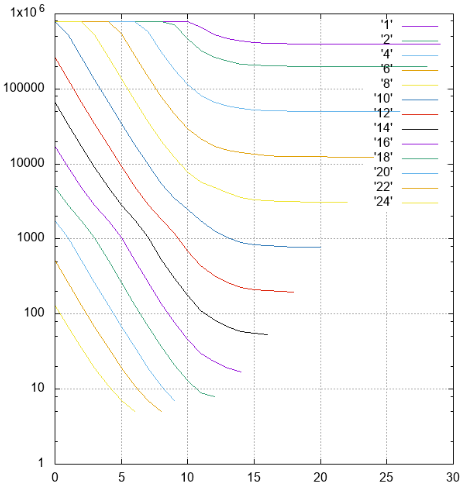Figura 4 Resultados, el número de páginas leídas en diferentes series

Por Y: el número de páginas leídas se pospone.
En X: cambio de tiras de la categoría más joven (48) a la categoría senior. Las rayas de diferentes anchos están firmadas y marcadas en diferentes colores.


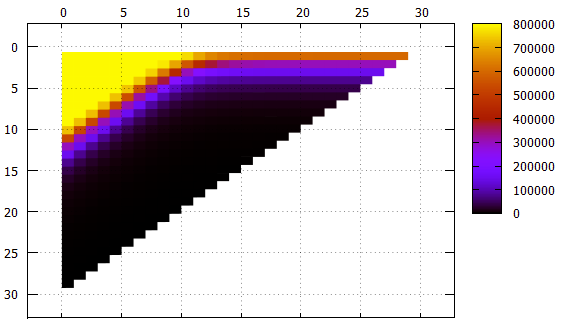Figura 5 Los mismos datos que la Figura 4, otra vista

X - cambio de banda
Y - ancho de banda

Lo que debe tenerse en cuenta:

• Aunque esto no es directamente visible en las imágenes, el índice funciona correctamente, es visible tanto en el número de elementos encontrados como en el contenido de los elementos mismos.
• todas las franjas con un ancho de no más de 10 con un desplazamiento de 0 requieren una lectura continua del índice
• Las franjas con un ancho de 1 a 18 con un aumento en el desplazamiento alcanzan la asíntota 2 ** (- N) del tamaño de todo el índice, lo cual es lógico
• para bandas más anchas de la asíntota: la altura del árbol, no puede haber menos lecturas
• se colocan un poco más de 1000 elementos en la página de la hoja de índice, esto se puede ver en una franja de ancho 10, que al cambiar 0 ya no requiere leer el índice completo, algunas páginas se pueden omitir
• El filtrado de bajo nivel funciona sorprendentemente bien. Considere una tira con un ancho de 10. Una opción de búsqueda ideal es con un desplazamiento de 20 (un total de 30 campos significativos), cuando no hay campos indefinidos en el prefijo, los datos se pueden encontrar con un solo haz. En esta situación, aproximadamente 1/1000 del índice se lee durante la búsqueda - 779 páginas.
  El caso intermedio es un desplazamiento de 10, tenemos un prefijo y un sufijo de 10 campos desconocidos. El número de páginas es de 2484, solo tres veces peor que en el caso ideal.
  E incluso en el peor de los casos, con un desplazamiento de 0 (un prefijo de 20 campos desconocidos), puede omitir algunas páginas.

En general, el algoritmo de indexación multidimensional puede reconocerse como eficiente incluso en un caso tan absurdo. Pero se considera la opción más infructuosa desde el punto de vista del índice lógico: estados equiprobables en todos los campos lógicos independientes.

Experimentar con datos reales

Tabla de operaciones , total 278,479,918 filas, datos de uno de los bucles de prueba.
Los resultados de algunas consultas en la tabla a continuación:


Leer / procesar una sola página requiere un promedio de 0.8 ms.

No es necesario describir el significado de consultas específicas, solo están aquí para demostrar la operatividad. Lo cual, por cierto, está confirmado.

Pero antes de que esta técnica pueda ser de uso práctico, queda mucho por hacer. Entonces, para continuar.