Aprendizaje de refuerzo profundo: cómo enseñar a las arañas a caminar

Hoy les contaré cómo apliqué algoritmos de refuerzo de aprendizaje profundo para controlar un robot. En resumen, le diré cómo crear una "caja negra con redes neuronales", que acepta la arquitectura del robot en la entrada y genera un algoritmo que puede controlarlo en la salida.

El núcleo de la solución es el algoritmo Advantage Actor Critic (A2C) con puntajes Advantage a través de la Estimación de ventaja generalizada (GAE).

Bajo el corte, las matemáticas, una implementación de TensorFlow y muchas demostraciones de qué tipo de algoritmos de caminar se redujeron.

Contenido:

- Conclusión

Desafío

En este artículo, le enseñaremos al robot a caminar en la simulación MuJoCo. Omitiremos la descripción del paso al crear un modelo del robot y la interfaz de Python con el entorno, porque No hay nada interesante allí. Para entenderlo, solo mire las demostraciones en MuJoCo y las fuentes de los entornos MuJoCo en Gym OpenAI .

En la entrada, el agente tendrá muchos números de MuJoCo: posiciones relativas, ángulos de rotación, velocidad, aceleración de partes del cuerpo del robot, etc. En total, el orden de ~ 800 características. Utilizamos el enfoque de aprendizaje profundo y no entenderemos lo que realmente significan. Lo principal es que en este conjunto de números habrá suficiente información para que el agente pueda entender lo que le está sucediendo.

En la salida, esperaremos 18 números, el número de grados de libertad del robot, lo que significa los ángulos de rotación de las bisagras en las que se fijan las extremidades.

Finalmente, el objetivo del agente es maximizar la recompensa total por el episodio. Terminaremos el episodio si el robot falla o si han pasado 3000 pasos (15 segundos). Cada paso recompensará al agente de acuerdo con la siguiente fórmula:

Es decir el objetivo del agente aumentará su coordenada $$$x$ y no caigas hasta el final del episodio.

Entonces, la tarea está establecida: encontrar la función $$$\ pi: \ R ^ {800} \ to \ R ^ {18}$ para lo cual la recompensa por el episodio será la mayor . Eso no suena muy bien? :) Veamos cómo Deep Reinforcement Learning maneja esta tarea.

¿Por qué el aprendizaje por refuerzo?

Los enfoques modernos para resolver el problema del movimiento de los robots que caminan consisten en prácticas de robótica clásica de las secciones de control óptimo y optimización de trayectoria : LQR, QP, optimización convexa. Leer más: Publicación del equipo de Boston Dynamics en Atlas .

Estas técnicas son una especie de "codificación rígida" porque requieren la introducción de muchos detalles de la tarea directamente en el algoritmo de control. No hay sistemas de aprendizaje en ellos, la optimización se lleva a cabo "en el acto".

Por otro lado, el aprendizaje por refuerzo (en adelante RL) no requiere hipótesis en el algoritmo, lo que hace que la solución al problema sea más general y escalable.

Declaración de aprendizaje por refuerzo

Fuente

En el problema de RL, consideramos la interacción del agente y el entorno como una secuencia de pares (estado, recompensa) y las transiciones entre ellos: acción .

Definir la terminología:

• $$$\ pi (a_t | s_t)$ - política , estrategia de comportamiento del agente, probabilidad condicional,
• $$$a_t \ sim \ pi (\ cdot | s_t)$ - la acción se considera una variable aleatoria de la distribución $$$\ pi$ ,
  Podríamos considerar la política como una función $$$\ pi: Estados \ a acciones$ , pero queremos que las acciones de los agentes sean estocásticas, lo que facilita la exploración . Es decir con cierta probabilidad no hacemos las acciones que el agente elige.
• $$$\ tau$ - trayectoria trazada por el agente, secuencia $$$(s_1, s_2, ..., s_n)$ .

La tarea del agente es maximizar el rendimiento esperado :

Ahora podemos formular el problema RL, encontrar:

donde $$$\ pi ^ *$ Es la política óptima.

Lea más en el material de OpenAI: OpenAI Spinning Up .

Gradiente de política

Es de destacar que una declaración rigurosa del problema de RL como un problema de optimización nos da la oportunidad de utilizar los métodos de optimización ya conocidos, por ejemplo, el descenso de gradiente . Solo imagine lo genial que sería si pudiéramos tomar el gradiente de retorno esperado por los parámetros del modelo : $$$\ nabla_ \ theta J (\ pi_ \ theta)$ . En este caso, la regla para actualizar las escalas sería simple:

Esta es precisamente la idea de todos los métodos de gradiente de políticas . La conclusión estricta de este gradiente es algo incondicional. No lo escribiremos aquí, pero dejamos un enlace al maravilloso material de OpenAI . El gradiente se ve así:

Por lo tanto, la pérdida de nuestro modelo será así:

Recordemos que $$$R (\ tau) = \ sum_ {t = 0} ^ T r_t$ y $$$\ pi_ \ theta (a_t | s_t)$ - esta es la salida de nuestra modelo en el momento en que ella estaba en $$$s_t$ . El menos apareció debido al hecho de que queremos maximizar $$$J$ . Durante el entrenamiento, consideraremos el gradiente en lotes y los agregaremos para reducir la variación (ruido de datos debido al entorno estocástico).

Este es un algoritmo de trabajo llamado REINFORCE . Y sabe cómo encontrar soluciones para algunos entornos simples. Por ejemplo, "CartPole-v1" .

Considere el código del agente:

class ActorNetworkDiscrete: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu) output_linear = tf.layers.dense(l1, units=action_space) output = tf.nn.softmax(output_linear) self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), axis=1) # Training output_log = tf.nn.log_softmax(output_linear) self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32) action_one_hot = tf.one_hot(self.action_ph, action_space) responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1) self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) actor = ActorNetworkDiscrete() 

Tenemos un pequeño perceptrón de esta arquitectura: (observación_espacio, 10, espacio_acción) [para CartPole esto es (4, 10, 2)]. tf.multinomial le permite elegir una acción ponderada al azar. Para obtener una acción, debe llamar:

 action = sess.run(actor.action_op, feed_dict={actor.state_ph: observation}) 

Y así lo entrenaremos:

 batch_generator = generate_batch(environments, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, total reward] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) 

El generador de lotes ejecuta el agente en el entorno y acumula datos para la capacitación. Los elementos del lote son tuplas de este tipo: $$$(s_t, a_t, R (\ tau))$ .

Escribir un buen generador es una tarea separada, donde la dificultad principal es el costo relativamente alto de llamar a sess.run () en comparación con un solo paso de simulación (incluso MuJoCo). Para acelerar el trabajo, puede aprovechar el hecho de que las redes neuronales se ejecutan en lotes y utilizan muchos entornos paralelos. Incluso lanzarlos secuencialmente en un hilo dará una aceleración significativa en comparación con un solo entorno.

 # Vectorized environments with gym-like interface from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv from baselines.common.vec_env.dummy_vec_env import DummyVecEnv def make_env(env_id, seed): def _f(): env = gym.make(env_name) env.reset() # Desync environments for i in range(int(200 * seed // environments_count)): env.step(env.action_space.sample()) return env return _f envs = [make_env(env_name, seed) for seed in range(environments_count)] # Can be switched to SubprocVecEnv to parallelize on cores # (for computationally heavy envs) envs = DummyVecEnv(envs) # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py def discount_cumsum(x, coef): """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def generate_batch(envs, batch_size, replay_buffer_size): envs_number = envs.num_envs observations = [[0 for i in range(observation_space)] for i in range(envs_number)] # [state, action, discounted reward-to-go] replay_buffer = np.empty((0,3), np.float32) # [state, action, reward] rollout lists for every environment instance rollouts = [np.empty((0, 3)) for i in range(envs_number)] while True: history = {'reward': [], 'max_action': []} replay_buffer = replay_buffer[batch_size:] # Main sampling cycle while len(replay_buffer) < replay_buffer_size: # Here policy acts in environments. Note that it chooses actions for all # environments in one batch, therefore expensive sess.run is called once. actions = sess.run(actor.action_op, feed_dict={actor.state_ph: observations}) observations_old = observations observations, rewards, dones, _ = envs.step(actions) history['max_action'].append(np.abs(actions).max()) time_point = np.array(list(zip(observations_old, actions, rewards))) for i in range(envs_number): # Regular python-like append rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) # Process done==True environments if dones.all(): print('WARNING: envs are in sync!! This makes sampling inefficient!') done_indexes = np.arange(envs_number)[dones] for i in done_indexes: rewards_trajectory = rollouts[i][:, 2].copy() history['reward'].append(rewards_trajectory.sum()) rollouts[i][:, 2] = discount_cumsum(rewards_trajectory, coef=discount_factor) replay_buffer = np.append(replay_buffer, rollouts[i], axis=0) rollouts[i] = np.empty((0, 3)) # Shuffle before yield to become closer to iid np.random.shuffle(replay_buffer) # Truncate replay_buffer to get the most relevant feedback from environment replay_buffer = replay_buffer[:replay_buffer_size] yield replay_buffer[:batch_size], history # Make a test yield a = generate_batch(envs, 8, 64) # Makes them of equal lenght for i in range(10): next(a) next(a)[0] 

El agente resultante puede jugar en entornos con un espacio finito de acciones . Este formato no es adecuado para nuestra tarea. El agente que controla el robot debe emitir un vector de $$$\ R ^ n$ donde $$$n$ - El número de grados de libertad. ( o puede dividir el espacio de acción en espacios y obtener una tarea con una salida discreta )

Políticas Diagonales Gaussianas

La esencia del enfoque de las Políticas Diagonales Gaussianas es que el modelo produzca parámetros de la distribución normal n-dimensional, a saber $$$\ mu_ \ theta$ - mat. esperando y $$$\ sigma_ \ theta$ - desviación estándar. Tan pronto como el agente necesite tomar una acción, le pediremos estos parámetros al modelo y tomaremos una variable aleatoria de esta distribución. Entonces hicimos salir al agente $$$\ R ^ n$ y lo hizo estocástico. Lo más importante es que después de haber fijado la clase de distribución en la salida, podemos calcular $$$\ log (\ pi_ \ theta (a_t | s_t))$ y, por lo tanto, gradiente de políticas.

Nota: se puede arreglar $$$\ sigma_ \ theta$ como hiperparámetro, reduciendo así la dimensión de salida. La práctica muestra que esto no causa mucho daño, sino que, por el contrario, estabiliza el aprendizaje.

Lea más sobre la política estocástica .

Código de agente:

 epsilon = 1e-8 def gaussian_loglikelihood(x, mu, log_std): pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi)) return tf.reduce_sum(pre_sum, axis=1) class ActorNetworkContinuous: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) mu = tf.layers.dense(l3, units=action_space) log_std = tf.get_variable(name='log_std', initializer=-0.5 * np.ones(action_space, std = tf.exp(log_std) self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std # Training self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32) action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std) self.loss = -tf.reduce_mean(action_logprob * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) 

La parte de entrenamiento no es diferente.

Ahora finalmente podemos ver cómo REINFORCE hará frente a nuestra tarea. En adelante, el objetivo del agente es moverse hacia la derecha.

Lenta pero seguramente arrastrándose hacia su objetivo.

Recompensa para llevar

Tenga en cuenta que hay miembros adicionales en nuestro gradiente. A saber para cada paso $$$t$ Al pesar el gradiente del logaritmo, usamos la recompensa total para toda la trayectoria . Por lo tanto, evaluar las acciones del agente por sus logros del pasado. Suena mal, ¿no? Por lo tanto esto

se convertirá en esto

Encuentra 10 diferencias :)

Si bien la presencia de estos miembros no estropea nada matemáticamente, hace mucho ruido para nosotros. Ahora, durante el entrenamiento, el agente prestará atención solo a las recompensas que recibió después de una acción específica .

Debido a esta mejora, la recompensa promedio ha crecido. Uno de los agentes recibidos aprendió a usar las extremidades anteriores para lograr su objetivo:

Reduzca la varianza agregando críticas

La esencia de otras mejoras es la reducción del ruido (varianza) que surge debido a las transiciones estocásticas entre los estados del medio.

Esto nos ayudará a agregar un modelo que prediga la cantidad promedio de recompensas recibidas por el agente, comenzando por el estado $$$s$ hasta el final de la trayectoria, es decir Función de valor.

La función Valor muestra el rendimiento esperado si nuestra política inicia el juego desde un estado específico. Lo mismo con la función Q, solo arregle la primera acción.

Añadir crítica

Así es como se ve el gradiente cuando se usa recompensa para llevar:

Ahora el coeficiente para el gradiente del logaritmo no es más que una muestra de la función Valor.

Pesamos el gradiente de logaritmo con una muestra de una trayectoria particular, lo que no es bueno. Podemos aproximar la función Valor con algún modelo, por ejemplo, una red neuronal, y pedirle el valor necesario, reduciendo así la varianza. Llamaremos a este modelo crítico (Crítico) y lo estudiaremos en paralelo con la política. Por lo tanto, la fórmula del gradiente se puede escribir como:

Redujimos la varianza, pero al mismo tiempo, introdujimos sesgo en nuestro algoritmo, ya que las redes neuronales pueden cometer errores de aproximación. Pero el compromiso en esta situación es bueno. Dichas situaciones en el aprendizaje automático se denominan compensación de sesgo-varianza .

El crítico enseñará la regresión de la función de valor en muestras de recompensa para llevar recolectadas en el entorno. Como una función de error, tomamos MSE. Es decir la pérdida se ve así:

Código crítico:

 class CriticNetwork: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) output = tf.layers.dense(l3, units=1) self.value_op = tf.squeeze(output, axis=-1) # Training self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op) optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate) self.update_op = optimizer.minimize(self.loss) 

El ciclo de entrenamiento ahora se ve así:

 batch_generator = generate_batch(envs, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, value, reward-to-go] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) # Train critic for j in range(10): _, critic_loss = sess.run([critic.update_op, critic.loss], feed_dict={critic.state_ph: batch[:, 0], critic.value_ph: batch[:, 3]}) 

Ahora el lote contiene otro valor, valor, calculado por el crítico en el generador.
Es decir El tipo de lote es este: $$$(s_t, a_t, V ^ \ pi_ \ psi (s_t), \ sum_ {t '= t} ^ T r_ {t'})$ .

En el ciclo, nada nos limita de entrenar al crítico a la convergencia , por lo que tomamos varios pasos de descenso de gradiente, mejorando así la aproximación de la función Valor y reduciendo el sesgo. Sin embargo, este enfoque requiere un gran tamaño de lote para evitar el reciclaje. Una afirmación similar sobre la política de aprendizaje no es cierta. Debería tener retroalimentación instantánea del entorno de aprendizaje, de lo contrario, podríamos encontrarnos en una situación en la que multemos la política por acciones que no hubiera tomado. Los algoritmos con esta propiedad se denominan on-policy .

Líneas de base en gradientes de políticas

Se puede demostrar que en el gradiente es permisible poner una amplia clase de otras funciones útiles de $$$t$ . Dichas funciones se denominan líneas de base . ( Conclusión de este hecho ) Las siguientes funciones funcionan bien como líneas de base:

Fuente: documento GAE .

Diferentes líneas de base dan diferentes resultados dependiendo de la tarea. Como regla general, la mayor ventaja viene dada por la función Ventaja y sus aproximaciones.

Incluso hay una pequeña intuición detrás de esto. Cuando usamos Advantage, multamos al agente en proporción a cuánto mejor o peor que el promedio que el agente considera la acción que realizó. Y cuanto mejor juega el agente en el medio ambiente, más altos se vuelven sus estándares . El agente ideal jugará bien y evaluará todas sus acciones como teniendo una ventaja igual a 0 y, por lo tanto, tendrá un gradiente igual a 0.

Evaluación de ventajas a través de la función de valor

Recordemos la definición de ventaja:

No está claro cómo aprender dicha función explícitamente. Un truco vendrá al rescate, que reducirá el cálculo de la función Advantage al cálculo de la función Value.

Definir $$$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - Diferencia temporal residual ( TD-residual ). No es difícil deducir que dicha función se aproxima a la Ventaja:

Tal cambio conceptualmente complejo provoca un cambio no tan grande en el código. Ahora, en lugar de evaluar la función Value, el crítico presentará una evaluación Advantage para capacitación en políticas.

El algoritmo resultante se llama Advantage Actor-Critic .

 def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + np.append(values[1:], np.array([0])) return deltas, values 

Los agentes obtenidos pueden observarse con confianza en la marcha y el uso sincrónico de las extremidades:

Estimación de ventaja generalizada

Un artículo relativamente reciente (2018), " Control continuo de alta dimensión utilizando el establecimiento de ventajas generalizadas ", ofrece una evaluación aún más eficiente de Advantage mediante la función Value. Reduce la varianza aún más:

donde:

• $$$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - TD-residual,
• $$$\ gamma$ - factor de descuento (hiperparámetro),
• $$$\ lambda$ - hiperparámetro.

La interpretación se puede encontrar en la publicación misma.

Implementación

 def discount_cumsum(x, coef): # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + discount_factor * np.append(values[1:], np.array([0])) advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor) return advantage, values 

Cuando se utiliza un tamaño de lote pequeño, el algoritmo converge a algunos óptimos locales. Aquí, el agente usa una pata como bastón, y el resto empuja:

Aquí, el agente no recurrió al uso de saltos, sino que simplemente tocó rápidamente las extremidades. Y también puedes ver cómo se comporta, si duda, se dará la vuelta y continuará corriendo:

El mejor agente, él está al comienzo del artículo. Salto estable, durante el cual todas las extremidades salen de la superficie. La capacidad desarrollada para equilibrar le permite al agente corregir la trayectoria a toda velocidad si se cometió un error:

Trampas

El aprendizaje automático es famoso por la dimensión del espacio de errores que se pueden cometer y obtener un algoritmo que no funciona. Pero RL lleva el problema a un nivel completamente nuevo.

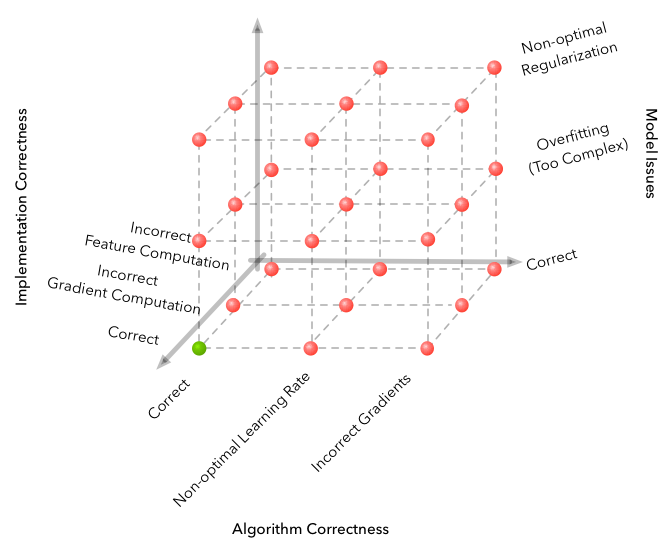
Fuente

Estas son algunas de las dificultades encontradas durante el desarrollo.

1. El algoritmo es sorprendentemente sensible a los hiperparámetros. Hubo un cambio en la calidad del aprendizaje al cambiar la tasa de aprendizaje de 3e-4 a 1e-4. Y la imagen cambió radicalmente, de un algoritmo completamente no convergente al mejor que hay en el video.
2. El tamaño del lote no es el mismo que en otras áreas de DL. Si en la clasificación de imágenes puede permitirse elegir el tamaño del lote 32-256 y el resultado no cambiará especialmente al aumentarlo, entonces es mejor tomar unos pocos miles, 3000 trabajos para nuestra tarea. Y nuevamente, desde la falta de convergencia hasta un buen algoritmo.
3. Aprender es mejor correr varias veces, a veces con semilla aleatoria no es afortunado.
4. Aprender en un entorno tan complejo lleva mucho tiempo y el progreso no es uniforme. Por ejemplo, el mejor algoritmo aprendido durante 8 horas, 3 de los cuales mostraron un peor resultado que una línea base aleatoria. Por lo tanto, al probar los algoritmos, es mejor comenzar con uno pequeño, como los entornos de juguete del gimnasio.
5. Un buen enfoque para encontrar hiperparámetros y arquitecturas de modelos sería mirar artículos e implementaciones relacionados. (Lo principal es no volver a entrenar)

Puede aprender más sobre los matices de Deep RL en este artículo: Deep Reinforcement Learning aún no funciona .

Conclusión

El algoritmo resultante resuelve convincentemente el problema. Función encontrada $$$\ pi: \ R ^ {800} \ to \ R ^ {18}$ , controlando con agilidad y confianza el robot.

Una continuación lógica será el estudio de parientes cercanos de los algoritmos A2C, PPO y TRPO. Mejoran la eficiencia de la muestra , es decir tiempo de convergencia del algoritmo, y son capaces de resolver problemas más complejos. Fue la aleatorización automática de dominios PPO + la que recientemente ensambló el cubo de Rubik en un robot .

Aquí puede encontrar el código del artículo: repositorio .

Espero que hayas disfrutado el artículo y te hayas inspirado en lo que Deep Reinforcement Learning puede hacer hoy.

Gracias por su atencion!

Enlaces utiles:

• ¡Bienvenido a Spinning Up en Deep RL!
• CS 294: Aprendizaje de refuerzo profundo, otoño de 2017
• CS 285: Aprendizaje de refuerzo profundo, toma de decisiones y control
• Control continuo de alta dimensión utilizando la ventaja de ventaja generalizada
• OpenAI Baselines: implementaciones de alta calidad de algoritmos de aprendizaje de refuerzo

Gracias a pinkotter , Vambala , andrey_probochkin , pollyfom y suriknik por ayudar con el proyecto.
En particular, Vambala y andrey_probochkin para crear un ambiente genial de MuJoCo.