
Hola habrozhiteli! ¿Es posible hablar de moda, fe o fantasía en ciencias básicas?
El universo no está interesado en la moda humana. Es imposible interpretar la ciencia como fe, porque los postulados científicos están constantemente sujetos a una rigurosa verificación experimental y se descartan en cuanto el dogma comienza a entrar en conflicto con la realidad objetiva. Y la fantasía generalmente descuida tanto los hechos como la lógica. Sin embargo, el gran Roger Penrose no quiere rechazar por completo estos fenómenos, porque la moda científica puede convertirse en un motor de progreso, la fe aparece cuando la teoría es confirmada por experimentos reales, y sin un vuelo de fantasía uno no puede comprender todas las rarezas de nuestro universo.
En el capítulo "Moda" aprenderás sobre la teoría de cuerdas, la teoría más de moda de las últimas décadas. "Faith" está dedicada a los dogmas en los que se basa la mecánica cuántica. Y "Fantasía" se refiere a tantas como teorías del origen del Universo conocido.
3.4. La paradoja del Big Bang
Primero, planteamos la cuestión de las observaciones. ¿Qué evidencia directa hay de que una vez que todo el Universo observable estaba en un estado extremadamente apretado e increíblemente caliente, de modo que fuera consistente con la imagen del Big Bang presentada en la sección 3.1? La evidencia más convincente es la radiación relicta (RI), a veces llamada el reflejo del Big Bang. La radiación de la reliquia es ligera, pero con una longitud de onda muy larga, por lo que es absolutamente imposible verla con los ojos. Esta luz se derrama sobre nosotros desde todos los lados de manera excepcionalmente uniforme (pero principalmente incoherente). Representa la radiación térmica con una temperatura de ~ 2.725 K, es decir, más de dos grados por encima del cero absoluto. Se cree que la "llamarada" observada se originó en un Universo increíblemente caliente (~ 3000 K en ese momento) aproximadamente 379,000 años después del Big Bang, en el momento de la última dispersión, cuando el Universo se volvió transparente a la radiación electromagnética (aunque esto no sucedió en absoluto durante el Big explosión; este evento cae en el primer 1/40 000 de la edad total del Universo, desde el Big Bang hasta la actualidad). Desde la era de la última dispersión, la longitud de estas ondas de luz ha aumentado aproximadamente tanto como el Universo se ha expandido (aproximadamente 1100 veces), por lo que la densidad de energía ha disminuido drásticamente. Por lo tanto, la temperatura observada de RI es de solo 2.725 K.
El hecho de que esta radiación es sustancialmente incoherente (es decir, térmica) se confirma de manera impresionante por la naturaleza misma de su espectro de frecuencia, que se muestra en la Fig. 3.13. Verticalmente, el gráfico muestra la intensidad de la radiación en cada frecuencia específica, y la frecuencia aumenta de izquierda a derecha. La curva continua corresponde al espectro de Planck de un cuerpo completamente negro, que se discutió en la Sección 2.2, para una temperatura de 2.725 K. Los puntos en la curva son los datos de observaciones específicas para las cuales se indican barras de error. Al mismo tiempo, las barras de error se incrementan en 500 veces, porque de lo contrario simplemente sería imposible considerarlas, incluso a la derecha, donde los errores alcanzan su máximo. La coincidencia entre la curva teórica y los resultados de las observaciones es simplemente maravillosa: tal vez esta sea la mejor coincidencia con el espectro térmico que se encuentra en la naturaleza.
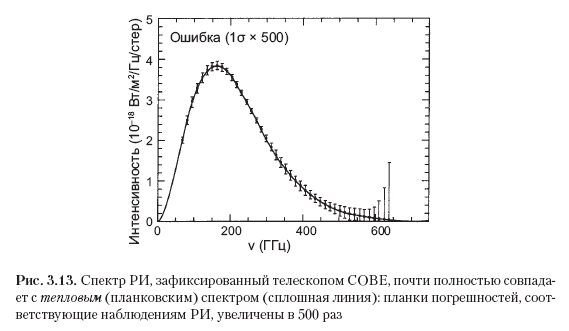
Sin embargo, ¿qué indica esta coincidencia? El hecho de que estemos considerando un estado que, aparentemente, estaba muy cerca del equilibrio termodinámico (por lo tanto, el término incoherente se utilizó anteriormente). Pero, ¿qué conclusión se desprende del hecho de que el nuevo universo estaba muy cerca del equilibrio termodinámico? De vuelta a la fig. 3.12 de la sección 3.3. ¡El área más grande con una partición de grano grueso (por definición) será mucho más grande que cualquier otra área y, como regla, es tan grande en comparación con el resto que excederá significativamente a todos en volumen! El equilibrio termodinámico corresponde a un estado macroscópico, que, presumiblemente, cualquier sistema llegará tarde o temprano. A veces se le llama la muerte térmica del Universo, pero en este caso, por extraño que parezca, deberíamos hablar sobre el nacimiento térmico del Universo. La situación se complica por el hecho de que el Universo recién nacido se estaba expandiendo rápidamente, por lo que el estado que estamos considerando no es un equilibrio. Sin embargo, la expansión en este caso puede considerarse esencialmente adiabática; en este momento, Tolman lo apreció completamente en 1934 [Tolman, 1934]. Esto significa que la entropía durante la expansión no cambió. (Una situación similar a esta, cuando el equilibrio termodinámico se mantiene debido a la expansión adiabática, puede describirse en el espacio de fases como un conjunto de regiones de tamaño de grano grueso de igual volumen, que difieren entre sí solo en volúmenes específicos del Universo. Podemos suponer que el estado máximo era característico de este estado primario entropía, ¡a pesar de la expansión!).
Aparentemente, nos enfrentamos a una paradoja excepcional. De acuerdo con los argumentos presentados en la Sección 3.3, la Segunda Ley requiere (y, en principio, esto lo explica) que el Big Bang debe ser un estado macroscópico con una entropía extremadamente baja. Sin embargo, las observaciones de RI, aparentemente, indican que el estado macroscópico del Big Bang se distinguió por una entropía colosal, tal vez incluso el máximo posible. ¿Dónde estamos tan seriamente equivocados?
Aquí está una de las explicaciones comunes para esta paradoja: se supone que dado que el Universo recién nacido era muy "pequeño", podría existir un cierto límite de entropía máxima, y el estado de equilibrio termodinámico, que, aparentemente, se mantuvo en ese momento, era simplemente un nivel límite posible entropía en ese momento. Sin embargo, esta es la respuesta incorrecta. Tal imagen podría corresponder a una situación completamente diferente, en la que las dimensiones del Universo dependerían de alguna restricción externa, por ejemplo, como en el caso del gas, que está encerrado en un cilindro con un pistón sellado. En este caso, la presión del pistón es proporcionada por algún mecanismo externo, que está equipado con una fuente externa (o salida) de energía. Pero esta situación no es aplicable al Universo en su conjunto, cuya geometría y energía, así como su "tamaño general", están determinados exclusivamente por la estructura interna y están controlados por las ecuaciones dinámicas de la teoría general de la relatividad de Einstein (incluidas las ecuaciones que describen el estado de la materia; ver secciones 3.1 y 3.2). En tales condiciones (cuando las ecuaciones son completamente deterministas e invariables con respecto a la dirección del tiempo, consulte la Sección 3.3), el volumen total del espacio de fase no puede cambiar con el tiempo. ¡Se supone que el espacio de fases P en sí mismo no debería "desarrollarse"! Toda la evolución se describe simplemente por la ubicación de la curva C en el espacio P y en este caso representa la evolución completa del Universo (ver sección 3.3).
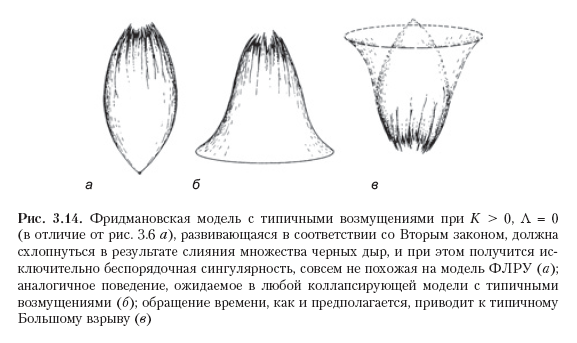
Quizás el problema se aclarará si consideramos las últimas etapas del colapso del Universo a medida que se acerca el Gran Choque. Recordemos el modelo de Friedman para K> 0, Λ = 0, presentado en la Fig. 3.2 a en la sección 3.1. Ahora creemos que las perturbaciones en este modelo surgen debido a la distribución irregular de la materia, y ya se han producido colapsos locales en algunas partes, donde permanecieron los agujeros negros. Entonces se debe suponer que después de eso, algunos agujeros negros se fusionarán entre sí y que el colapso en una singularidad finita resultará ser un proceso extremadamente complejo que no tiene casi nada que ver con el Big Crash estrictamente simétrico del modelo de Friedmann simétrico perfectamente esférico que se muestra en la Fig. 3.6 a. Por el contrario, en un sentido cualitativo, la situación de colapso recordará mucho más la grandiosa mezcolanza que se muestra en la Fig. 3.14 a; La singularidad resultante que surge en este caso puede ser algo consistente con la hipótesis BKLM mencionada al final de la Sección 3.2. El estado de colapso final tendrá una entropía inimaginable, a pesar del hecho de que el Universo nuevamente se reducirá a tamaños pequeños. Aunque es precisamente un modelo de Friedmann reclasificado (espacialmente cerrado) que ahora no se considera una opción plausible para representar nuestro propio Universo, las mismas consideraciones se aplican a otros modelos de Friedmann, con o sin una constante cosmológica. La variedad colapsada de cualquier modelo de este tipo, que experimenta perturbaciones similares debido a la distribución desigual de la materia, nuevamente, debería convertirse en un caos que todo lo consume, una singularidad como un agujero negro (Fig. 3.14 b). Al retroceder el reloj en cada uno de estos estados, llegamos a la posible singularidad inicial (potencial Big Bang), que, en consecuencia, tiene una entropía colosal, que contradice la suposición aquí sobre el "techo" de la entropía (Fig. 3.14 c).
Aquí debo pasar a posibilidades alternativas, que a veces también se consideran. Algunos teóricos sugieren que la segunda ley debe revertirse de alguna manera en tales modelos colapsantes, de modo que la entropía total del Universo se haga más pequeña (después de la expansión máxima) a medida que se acerca el Big Crash. Sin embargo, es especialmente difícil imaginar una imagen de este tipo en presencia de agujeros negros, que, si se forman, ellos mismos trabajarán para aumentar la entropía (debido a la asimetría del tiempo en la disposición de conos cero cerca del horizonte de eventos, ver Fig. 3.9). Esto continuará en un futuro lejano, al menos hasta que los agujeros negros se evaporen bajo la influencia del mecanismo de Hawking (ver secciones 3.7 y 4.3). En cualquier caso, tal posibilidad no niega los argumentos presentados aquí. Hay otro problema importante que está asociado con modelos de colapso tan complejos y en el que los lectores mismos pueden haber pensado: las singularidades de los agujeros negros pueden no surgir al mismo tiempo, por lo que cuando el tiempo se invierte, no obtendremos el Big Bang, lo que sucede "todo y de inmediato ". Sin embargo, tal es una de las propiedades (aún no probadas, pero convincentes) de la hipótesis de una fuerte censura cósmica [Penrose, 1998a; PKR, sección 28.8], según la cual, en el caso general, dicha singularidad será similar al espacio (sección 1.7) y, por lo tanto, puede considerarse un evento de una sola vez. Además, independientemente de la validez de la fuerte hipótesis de la censura cósmica, se conocen muchas soluciones que satisfacen esta condición, y todas esas opciones (cuando se expanden) tendrán valores de entropía relativamente altos. Esto reduce significativamente el grado de preocupación sobre la validez de nuestros hallazgos.
En consecuencia, no encontramos evidencia de que, dadas las pequeñas dimensiones espaciales del Universo, un cierto "techo bajo" de posible entropía necesariamente existiría en él. En principio, la acumulación de materia en forma de agujeros negros y la fusión de singularidades de "agujero negro" en un solo caos singular es un proceso que concuerda perfectamente con la segunda ley, y este proceso final debería ir acompañado de un tremendo aumento de la entropía. El "pequeño" según los estándares geométricos, el estado final del Universo puede tener una entropía inimaginable, mucho más alta que en las etapas relativamente tempranas de un modelo cosmológico colapsante, y la miniatura espacial en sí misma no establece un "techo" para el valor máximo de la entropía, aunque tal "techo" ( al invertir el paso del tiempo) podría explicar por qué la entropía fue extremadamente pequeña durante el Big Bang. De hecho, dicha imagen (Fig. 3.14 a, b), que muestra el colapso del Universo en general, sugiere una pista de la paradoja: por qué el Big Bang tuvo una entropía extremadamente baja en comparación con lo que pudo haber sido, a pesar del hecho de que la explosión caliente (y tal estado debería tener la máxima entropía). La respuesta radica en el hecho de que la entropía puede aumentar radicalmente si se permiten desviaciones graves de la homogeneidad espacial, y el mayor aumento de este tipo está asociado con las no uniformidades causadas precisamente por la aparición de agujeros negros. En consecuencia, el Big Bang espacialmente homogéneo podría tener, relativamente hablando, una entropía increíblemente baja, a pesar de que su contenido era increíblemente caliente.
Una de las pruebas más convincentes a favor del hecho de que el Big Bang fue realmente bastante homogéneo desde un punto de vista espacial, lo cual está en buen acuerdo con la geometría del modelo FLRU (pero no con el caso mucho más general de singularidad desordenada, ilustrada en la figura 3.14 c), se asocia nuevamente con RI, pero esta vez con su homogeneidad angular, y no con la naturaleza termodinámica. Tal uniformidad se manifiesta en el hecho de que la temperatura de la radiación es prácticamente la misma en cualquier parte del cielo, y las desviaciones de la uniformidad no son más de 10–5 (ajustadas por el pequeño efecto Doppler asociado con nuestro movimiento a través de la materia circundante). Además, existe una uniformidad casi universal en la distribución de galaxias y otras materias; Por lo tanto, la distribución de bariones (ver Sección 1.3) en una escala suficientemente grande se caracteriza por una homogeneidad significativa, aunque existen anomalías notables, en particular los llamados vacíos, donde la densidad de la materia visible es radicalmente más baja que el promedio. En general, se puede argumentar que la homogeneidad resulta ser mayor, cuanto más miramos hacia el pasado del Universo, y RI es la evidencia más antigua de la distribución de la materia, que podemos observar directamente.
Esta imagen es consistente con el punto de vista según el cual, en las primeras etapas de desarrollo, el Universo era de hecho extremadamente homogéneo, pero con una densidad ligeramente irregular. Con el tiempo (y bajo la influencia de varios tipos de "fricción", procesos que ralentizan los movimientos relativos), estas irregularidades de densidad se amplificaron bajo la influencia de la gravedad, lo cual es consistente con la idea de un agrupamiento gradual de la materia. Con el tiempo, el agrupamiento aumenta, como resultado, se forman estrellas; se agrupan en galaxias, en el centro de cada una de las cuales se forma un agujero negro masivo. En última instancia, este agrupamiento se debe al efecto inevitable de la gravedad. Tales procesos están realmente asociados con un fuerte aumento de la entropía y demuestran que, teniendo en cuenta la gravedad, esa bola brillante prístina, de la que solo queda hoy RI, podría tener una entropía máxima. La naturaleza térmica de esta pelota, como lo demuestra el espectro de Planck que se muestra en la Fig. 3.13, solo habla de esto: si consideramos el Universo (en la época de la última dispersión) simplemente como un sistema que consiste en materia y energía que interactúan entre sí, entonces podemos suponer que realmente estaba en equilibrio termodinámico. Sin embargo, si se tienen en cuenta las influencias gravitacionales, la imagen cambia dramáticamente.

Si imaginamos, por ejemplo, gas en un recipiente hermético, es natural suponer que alcanzará la máxima entropía en ese estado macroscópico cuando se distribuye uniformemente por todo el recipiente (Fig. 3.15 a). En este sentido, se parecerá a una bola al rojo vivo que generó el IR, que se distribuye uniformemente por todo el cielo. Sin embargo, si reemplazamos las moléculas de gas con un extenso sistema de cuerpos conectados por gravedad, por ejemplo, estrellas individuales, obtenemos una imagen completamente diferente (Fig. 3.15 b). Debido a los efectos gravitacionales, las estrellas se distribuyen de manera desigual en forma de cúmulos. Finalmente, la mayor entropía se logrará cuando numerosas estrellas colapsen o se fusionen en agujeros negros. A pesar del hecho de que este proceso puede llevar mucho tiempo (aunque será promovido por la fricción debido a la presencia de gas interestelar), veremos que al final, cuando la gravedad domina, la entropía es mayor, cuanto menos uniformemente se distribuye la sustancia en el sistema.
Dichos efectos se pueden rastrear incluso a nivel de la experiencia cotidiana. Se puede hacer una pregunta: ¿cuál es el papel de la Segunda Ley en el mantenimiento de la vida en la Tierra? A menudo puedes escuchar que vivimos en este planeta gracias a la energía recibida del sol. Pero esta no es una afirmación completamente cierta, si consideramos la Tierra como un todo, ya que casi toda la energía recibida por la Tierra durante el día pronto desaparece nuevamente en el espacio, en el oscuro cielo nocturno. (Por supuesto, el equilibrio exacto se corregirá ligeramente bajo la influencia de factores como el calentamiento global y el calentamiento del planeta bajo la influencia de la desintegración radiactiva). De lo contrario, ¡la Tierra simplemente se calentaría más y más y quedaría deshabitada en unos pocos días! Sin embargo, los fotones recibidos directamente del Sol tienen una frecuencia relativamente alta (están concentrados en la parte amarilla del espectro), y la Tierra emite al espacio muchos fotones de baja frecuencia relacionados con el espectro infrarrojo. De acuerdo con la fórmula de Planck (E = hν, consulte la Sección 2.2), cada uno de los fotones por separado del Sol tiene una energía mucho más alta que los fotones emitidos al espacio, por lo tanto, para lograr un equilibrio, muchos más fotones deberían abandonar la Tierra de lo que llegan (ver Fig. 3.16). Si llegan menos fotones, la energía entrante tendrá menos grados de libertad, y la energía saliente tendrá más, y, por lo tanto, de acuerdo con la fórmula de Boltzmann (S = k log V), los fotones entrantes tendrán una entropía mucho menor que los salientes. Utilizamos energía de baja entropía contenida en las plantas para reducir nuestra propia entropía: comemos plantas o herbívoros. Entonces la vida en la Tierra se conserva y prospera. (Aparentemente, estos pensamientos fueron formulados claramente por primera vez por Erwin Schrödinger en 1967, quien escribió su revolucionario libro "La vida como es" [Schrödinger, 2012]).
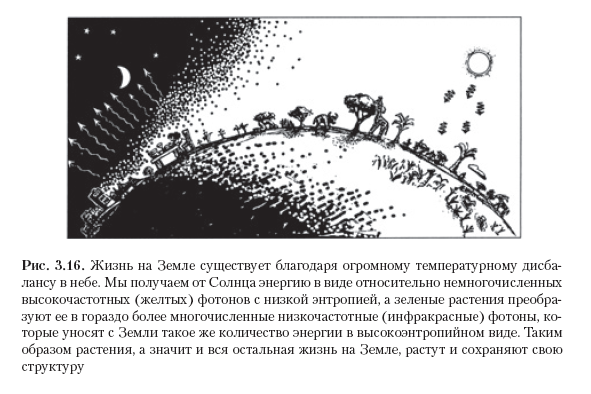
El hecho más importante asociado con este equilibrio de baja entropía es este: el sol es un punto caliente en un cielo completamente oscuro. ¿Pero cómo son estas condiciones? , . ., , . , ( , ) , .
, , -, 85 % (-Λ) , , . , (. 3.6, 3.7, 3.9, , , . 4.3). , . , , , .
— — . , , , . , , , , : - . () , , -, . , , , , - !
, . , , (. . 3.15 ). 3.6. , , : - ( - K
0, . 3.1) . , , .
»
»
Contenidos»
Extracto25% —
New ScienceTras el pago de la versión en papel del libro, se envía un libro electrónico por correo electrónico.