Conteo de la comunidad "¿Qué?" Donde ¿Cuándo? ”(ChGK) o cuántos apretones de manos ante un amigo?

Hola Habr!

Las vacaciones de año nuevo son un buen momento para tomar un descanso de TI Utiliza habilidades profesionales en tu pasatiempo favorito. Buscando en el sitio de la clasificación deportiva ChGK , encontré una excelente API que le permite obtener datos sobre todos los juegos de todos los torneos. Entonces tuve la idea de construir un gráfico de la comunidad de expertos y probar la teoría de seis apretones de manos en una comunidad geográficamente dispersa y estrictamente fuera de línea. Bajo katom imágenes de gráficos y estadísticas inútiles.

Para empezar, un breve programa educativo, qué es el deporte ChGK.

Recuperación de datos

Asumimos que los jugadores están familiarizados entre sí si jugaron al menos una vez en una mesa de juego. Gracias a la buena API, descargar datos sobre todos los torneos y todos los equipos no es un problema.

Debajo de los spoilers, ni siquiera se usa Beautiful Soup, solo solicitudes. Un cuaderno jupyter con todo el código fuente estará al final del artículo.

url = 'https://rating.chgk.info/api/tournaments.json/?page={}' df = pd.DataFrame(columns=['name', 'start']) for i in range(1, 7): data = requests.get(url.format(i)).json() for item in data["items"]: df.loc[item["idtournament"]] = (item["name"], item["date_start"]) df.to_csv('tournaments.csv') 

Queda por descargar las listas de juegos de todos los torneos y recordar a todos los conocidos. Inicialmente, planeé almacenar los hechos de un juego conjunto en un DataFrame, pero la velocidad de agregar nuevos registros fue deprimente. Por lo tanto, estableceremos a partir de tuplas (id1, id2), donde id1, id2 son los identificadores de jugadores que están familiarizados entre sí. Al mismo tiempo, elimine los duplicados.

 df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0') url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json' links = set() for id in df.index: teams = requests.get(url.format(id)).json() for team in teams: t = team["recaps"] for i in range(len(t)): for j in range(i + 1, len(t)): first = int(t[i]["idplayer"]) second = int(t[j]["idplayer"]) if first < second: links.add((first, second)) else: links.add((second, first)) #    sleep(1) clear_output(wait=True) display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df))) display('Links total: ' + str(len(links))) 

Obtener un gráfico y explorar componentes conectados

Entonces, la preparación de datos ha terminado, ¡es hora de construir un gráfico! Para hacer esto, utilizaremos la biblioteca networkx , cuyas capacidades son suficientes para nuestro clúster.

 players = itertools.chain(*links) G = nx.Graph() G.add_nodes_from(players) for t in links: G.add_edge(*t) print(nx.info(G)) 

Ahora hay alrededor de doscientas mil personas en la comunidad ChGK, y en promedio, un experto en una carrera ha jugado con 12 personas:

 Number of nodes: 198145 Number of edges: 1206076 Average degree: 12.1737 

Es hora de descubrir cuántos componentes conectados hay en el gráfico de citas. Networkx tiene una gran función llamada connected_components que hace justo lo que necesita:

 clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)] print(clusters_l[:20]) 

Casi las tres cuartas partes de los jugadores están en un componente conectado, el resto se divide en subgráficos muy pequeños. Hay más de ocho mil de ellos.

 [145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35] 

Incluso en una escala logarítmica, el dominio del componente principal se ve impresionante. En el eje X, el número del componente del mayor al menor, en el eje Y, su tamaño (el eje es logarítmico).

¿Qué causó una distribución tan desigual de personas en componentes conectados? En mi opinión, el punto es este:

• un pequeño grupo de personas viene al juego por primera vez y, por lo tanto, forma un pequeño grupo para 4-6 personas;
• si la ciudad ya tiene una comunidad grande, dicho grupo se fusionará rápidamente con el principal: solo una persona necesita jugar para un equipo del grupo principal;
• si en la ciudad de ChGK acaba de aparecer, el grupo vivirá más tiempo, porque Jugar para un equipo del grupo principal es más difícil.

El proceso se asemeja a la formación de gotas de lluvia en las nubes: una gran gota atrae a las pequeñas y crece rápidamente.

Antes de tratar con el componente principal, veamos los componentes en primer o noveno lugar (considero que el componente principal es cero). Probamos la hipótesis de que las personas en estos componentes son de la misma ciudad. El conocedor no tiene ningún apego a la ciudad (lo cual es lógico en nuestro mundo moderno). Sin embargo, puedes mirar el puerto de origen del equipo para el que jugó por última vez

 for i in range(1, 10): _g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i]) s = pd.Series() p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json' t_url = 'https://rating.chgk.info/api/teams/{}.json' for player in _g: data = requests.get(p_url.format(player)).json() for item in data: team_id = data[item]["tournaments"][0]["idteam"] data = requests.get(t_url.format(team_id)).json() town = data[0]["town"] s.at[len(s)] = town print(' #{}'.format(i)) print(s.value_counts()) 

Placa resumen:

Sí, los pequeños grupos son casi en su totalidad de una ciudad. Preste atención al componente de setenta y dos residentes de Tambov, que está asociado con Luxemburgo. En el séptimo y noveno lugar se encuentran los componentes de Gorno-Altaysk, que por alguna razón no están interconectados. Me imagino fácilmente la lucha de dos clanes de cenizas ChGK, como Montecca y Capulet, que luchan por el control de la ciudad.
Supongo que en un futuro cercano estos componentes se fusionarán en el principal pero continuará luchando .

El componente principal de la conectividad.

Entonces, llegamos al componente principal. Obtendremos el subgráfico deseado y miraremos sus estadísticas:

 subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0]) subgraph = G.subgraph(subgraph_v) print(nx.info(subgraph)) 

El número promedio de conexiones resultó ser más.

 Number of nodes: 145922 Number of edges: 1070504 Average degree: 14.6723 

¿Y cuál es el número máximo de conexiones por jugador?

 for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]: print(' {}   {} '.format(t[0], t[1])) 

  42511   818   15051   798   29800   678   23020   666   16581   662   5328   657   29887   651   15811   645   30352   605   1055   602  

Francamente, estoy un poco sorprendido por los números. Si juegas con un equipo nuevo cada vez, necesitarás 818/5 ≈ 164 juegos para llegar al primer lugar. Increíble
Recordaremos a los dos primeros expertos en esta calificación y utilizaremos más sus habilidades de comunicación.
Calculemos cuántos conocidos más cercanos tiene un experto promedio:

 _count = 50 values = nx.degree_histogram(subgraph) plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),values[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(0,_count, 5)) plt.ylabel(' ', fontsize=18) plt.title(' ', fontsize=22) plt.show() 

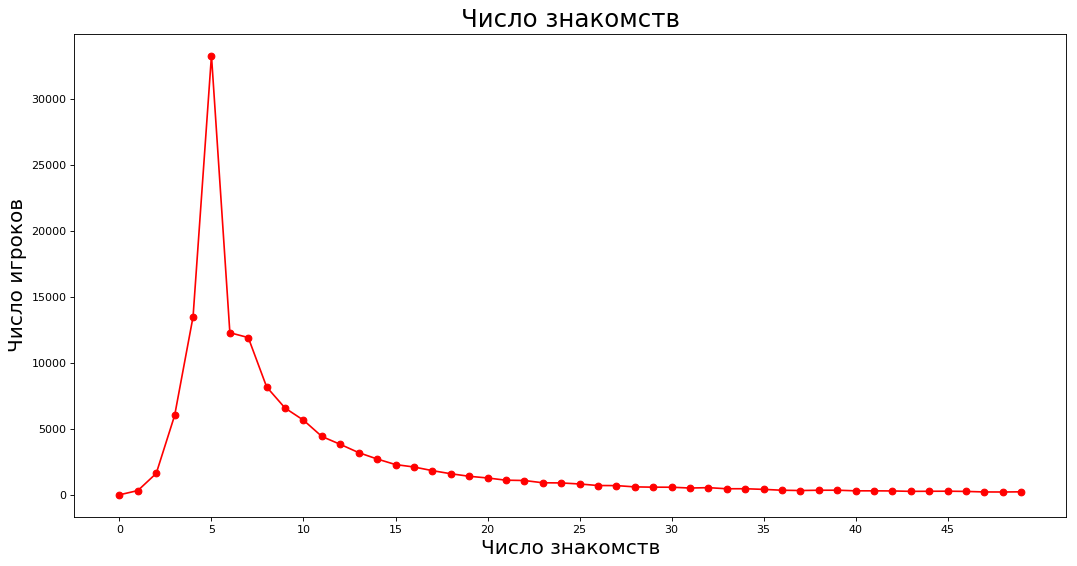
En el eje X, el número de conocidos más cercanos, en el eje Y, el número de expertos que tiene el número correspondiente de conocidos. Por ejemplo, aproximadamente 40,000 expertos tienen cada uno cinco conocidos.
Tenga en cuenta que la moda tiene 5 conocidos (es curioso que hasta seis personas puedan estar en la mesa). Al mismo tiempo, el promedio aritmético del número de conocidos es 14.67, y la mediana es 7. El hecho es que los caballeros de la clasificación anterior sobreestiman en gran medida el promedio. Si cien personas no juegan en ChGK, y una tiene 800 conocidos, entonces, en promedio, juegan en ChGK.

Distancias a los jugadores

Porque contar el diámetro de un gráfico de este tipo es un poco difícil , hagámoslo más fácil: tome una lista de varios jugadores y encuentre el máximo de las distancias más cortas entre ellos y otros expertos. Como estos jugadores, tomé varios expertos conocidos, yo mismo, un jugador aleatorio y dos expertos con el mayor número de conocidos (ver calificación arriba). Esto es lo que sucedió:

 famous_players = {9808: ' ', 5195: ' ', 25882: ' ', 29333: ' ', 118622: ' ', 42511: ' ', 15051: ' ', 118621: ' '} for key in famous_players: print('{}: {} -      ' .format(famous_players[key], nx.eccentricity(subgraph, v=key))) 

  : 12 -        : 12 -        : 12 -        : 12 -        : 13 -        : 12 -        : 13 -        : 13 -       

Resulta que una formulación sólida de la teoría de seis apretones de manos (dos personas separadas por no más de cinco niveles de amigos mutuos) es incorrecta. El diámetro del gráfico es muy probablemente 13-14.
¿Qué pasa con una redacción más débil (dos personas en promedio están separadas por no más de cinco niveles de amigos mutuos)?

 for key in famous_players: paths = nx.shortest_path_length(subgraph, source=key).values() print('{}: {} -      ' .format(famous_players[key], sum(paths) / len(paths))) 

  : 3.941461876893135 -        : 3.7971107852140182 -        : 3.89353216101753 -        : 3.8634887131481204 -        : 4.1443373857266215 -        : 3.575478680390894 -        : 3.608674497334192 -        : 4.564102739819904 -       

Si aflojamos la redacción, entonces la teoría se cumple, en promedio entre expertos en 4-5 niveles de conocidos. Trazamos cuántas personas están familiarizadas con el conocedor aleatorio A. Druzem directamente, a través de uno, dos, etc. entendidos

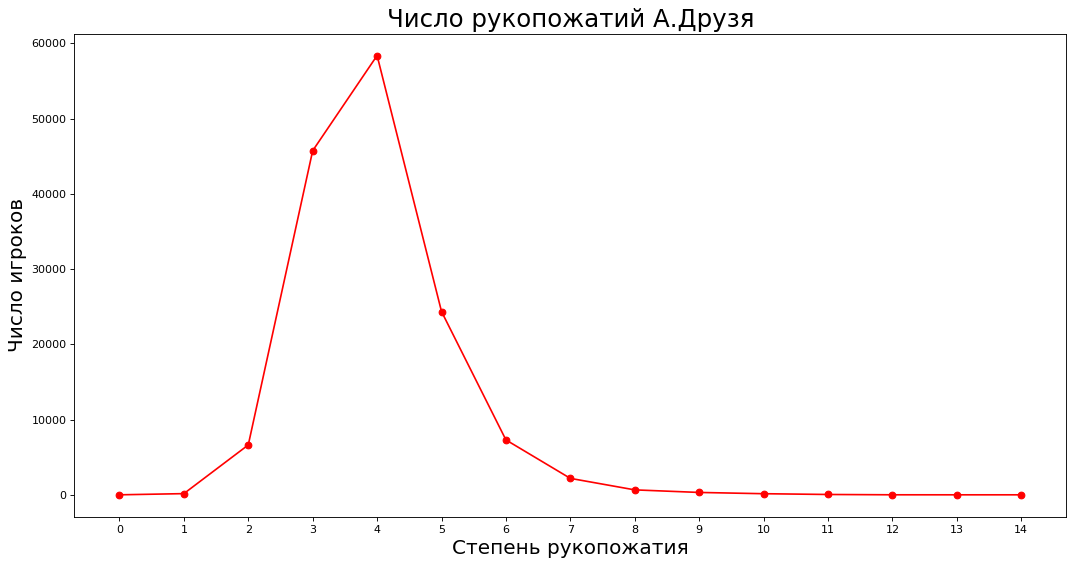
 paths = nx.shortest_path_length(subgraph, source=9808) neighbours = [0] * 15 for k in paths: neighbours[paths[k]] += 1 _count = 15 plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(_count)) plt.ylabel(' ', fontsize=18) plt.title('  .', fontsize=22) plt.show() 

En el eje X, el grado de conocimiento de A. Druzem (directamente, a través de uno, dos, etc.), en el eje Y, el número de expertos que están familiarizados con A. Druzem de esta manera.

Gráficos sociales

Porque construir un gráfico para casi 200 mil personas no es una buena idea, lo haremos más fácil: construiremos el componente de conectividad Kerch y un gráfico de personas asociadas con el autor.

Componente Kerch

 little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1]) little = G.subgraph(little_v) plt.figure(figsize=(24, 12), dpi=200) pos = nx.kamada_kawai_layout(little) nx.draw(little, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet) plt.show() 

Puede ver la separación de componentes en equipos. Además, los equipos están interconectados con la ayuda, por regla general, de uno o dos conocedores sociables. En el centro hay un núcleo bastante pequeño de expertos que jugaron con una gran cantidad de otros jugadores.

Cuenta de una persona

Encontraremos los conocidos más cercanos de una persona y veremos cómo están relacionados. Para simplificar el gráfico, no agregaremos a la persona (ya está conectado con todos)

 id = 118622 ego_graph = [n for n in G.neighbors(id)] #ego_graph.append(id) ego_graph = G.subgraph(ego_graph) plt.figure(figsize=(24, 16), dpi=200) pos = nx.kamada_kawai_layout(ego_graph) nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet) plt.show() 

El gráfico es mucho más denso, se puede distinguir un núcleo de 10-15 personas que están familiarizadas entre sí. El tamaño máximo de clic es 13.

Conclusión

• Es mucho más difícil conocer a una persona en el deporte ChGK que en una red social, necesita desconectarse y jugar al menos un torneo. Al mismo tiempo, los expertos están dispersos por todo el mundo. Sin embargo, la distancia promedio entre expertos es de hecho menos de cinco.
• El sitio de calificación utiliza el número Snyatkovsky , que es un análogo del número Erdös en el mundo de ChGK. El propio Sr. Snyatkovsky ocupa el tercer lugar en nuestro ranking de los conocedores más sociables.
• Código de un artículo en mi github .
• Por sus valiosos comentarios, el autor agradece al White Noise y Who Framed Roger Federer, Mikhail Akulov, Vera Terentyeva y Firemoon .