Introduciendo el método de retropropagación

Hola a todos! Las vacaciones de Año Nuevo han llegado a su fin, lo que significa que estamos nuevamente listos para compartir material útil con usted. Se preparó una traducción de este artículo en previsión del lanzamiento de una nueva transmisión en el curso "Algoritmos para desarrolladores" .

Vamos!

---

El método de error de propagación hacia atrás es probablemente el componente más fundamental de una red neuronal. Fue descrita por primera vez en la década de 1960 y casi 30 años después fue popularizada por Rumelhart, Hinton y Williams en un artículo titulado "Aprendizaje de representaciones por errores de propagación inversa" .

El método se usa para entrenar de manera efectiva una red neuronal usando la llamada regla de la cadena (la regla de diferenciación de una función compleja). En pocas palabras, después de cada pasada a través de la red, la propagación inversa realiza una pasada en la dirección opuesta y ajusta los parámetros del modelo (pesos y desplazamientos).

En este artículo, me gustaría considerar en detalle desde un punto de vista matemático el proceso de aprendizaje y optimización de una red neuronal simple de 4 capas. Creo que esto ayudará al lector a comprender cómo funciona la propagación hacia atrás, así como a darse cuenta de su importancia.

Definiendo un modelo de red neuronal

La red neuronal de cuatro capas consta de cuatro neuronas en la capa de entrada, cuatro neuronas en las capas ocultas y 1 neurona en la capa de salida.


Una imagen simple de una red neuronal de cuatro capas.

Capa de entrada

En la figura, las neuronas moradas representan la entrada. Pueden ser cantidades escalares simples o más complejas: vectores o matrices multidimensionales.


Ecuación que describe las entradas xi.

El primer conjunto de activaciones (a) es igual a los valores de entrada. "Activación" es el valor de una neurona después de aplicar la función de activación. Ver abajo para más detalles.

Capas ocultas

Los valores finales en las neuronas ocultas (en la figura verde) se calculan utilizando entradas ponderadas z ^l en la capa I y activaciones ^I en la capa L. Para las capas 2 y 3, las ecuaciones serán las siguientes:

Para l = 2:



Para l = 3:



W ² y W ³ son los pesos en las capas 2 y 3, y b ² y b ³ son los desplazamientos en estas capas.

Las activaciones a ² y a ³ se calculan utilizando la función de activación f. Por ejemplo, esta función f es no lineal (como sigmoide , ReLU y tangente hiperbólica ) y permite a la red estudiar patrones complejos en los datos. No nos detendremos en cómo funcionan las funciones de activación, pero si está interesado, le recomiendo leer este maravilloso artículo .

Si observa detenidamente, verá que todas las x, z ² , a ² , z ³ , a ³ , W ¹ , W ² , b ¹ y b ² no tienen los índices más bajos que se muestran en la figura de la red neuronal de cuatro capas. El hecho es que combinamos todos los valores de los parámetros en matrices agrupadas por capas. Esta es una forma estándar de trabajar con redes neuronales, y es bastante cómoda. Sin embargo, revisaré las ecuaciones para que no haya confusión.

Tomemos la capa 2 y sus parámetros como ejemplo. Las mismas operaciones se pueden aplicar a cualquier capa de la red neuronal.
W ¹ es la matriz de pesos de dimensión (n, m) , donde n es el número de neuronas de salida (neuronas en la capa siguiente) ym es el número de neuronas de entrada (neuronas en la capa anterior). En nuestro caso, n = 2 ym = 4 .



Aquí, el primer número en el subíndice de cualquiera de los pesos corresponde al índice de neurona en la siguiente capa (en nuestro caso, esta es la segunda capa oculta), y el segundo número corresponde al índice de neurona en la capa anterior (en nuestro caso, esta es la capa de entrada).

x es el vector de entrada de dimensión ( m , 1), donde m es el número de neuronas de entrada. En nuestro caso, m = 4.



b ¹ es el vector de desplazamiento de dimensión ( n , 1), donde n es el número de neuronas en la capa actual. En nuestro caso, n = 2.



Siguiendo la ecuación para z ^2, podemos usar las definiciones anteriores de W ¹ , x y b ¹ para obtener la ecuación z ² :



Ahora mire cuidadosamente la ilustración de la red neuronal arriba:



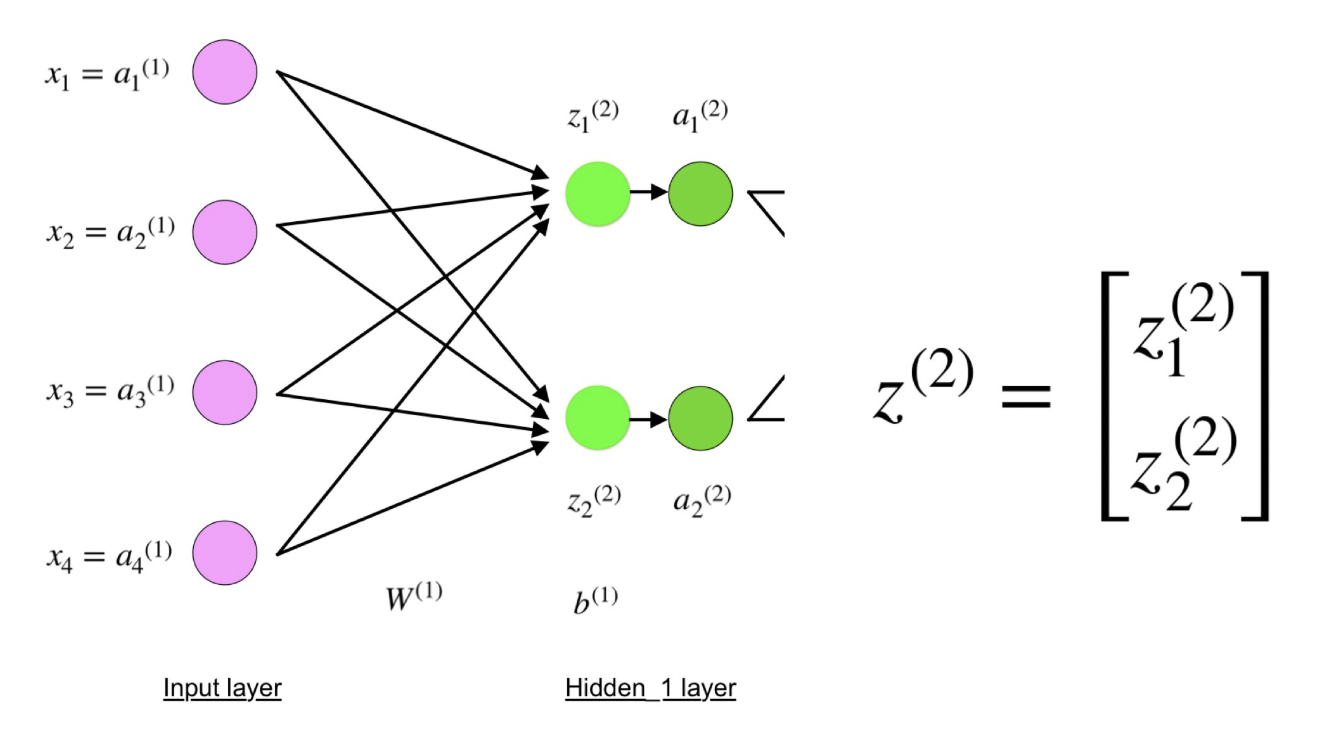
Como puede ver, z ² puede expresarse en términos de z ₁ ² y z ₂ ² , donde z ₁ ² y z ₂ ² son las sumas de los productos de cada valor de entrada x ⁱ por el peso correspondiente W _ij ¹ .

Esto lleva a la misma ecuación para z ² y demuestra que las representaciones matriciales z ² , a ² , z ³ y a ³ son verdaderas.

Capa de salida

La última parte de la red neuronal es la capa de salida, que proporciona el valor predicho. En nuestro ejemplo simple, se presenta en forma de una sola neurona teñida de azul y se calcula de la siguiente manera:



Nuevamente, usamos la representación matricial para simplificar la ecuación. Puede usar los métodos anteriores para comprender la lógica subyacente.

Distribución directa y evaluación

Las ecuaciones anteriores forman una distribución directa a través de la red neuronal. Aquí hay un resumen rápido:



(1) - capa de entrada
(2) - el valor de la neurona en la primera capa oculta
(3) - valor de activación en la primera capa oculta
(4) - el valor de la neurona en la segunda capa oculta
(5) - valor de activación en el segundo nivel oculto
(6) - capa de salida

El paso final en el pase directo es evaluar el valor de salida previsto s relativo al valor de salida esperado y .

La salida y es parte del conjunto de datos de entrenamiento (x, y), donde x es la entrada (como recordamos de la sección anterior).

La estimación entre sy e ocurre a través de la función de pérdida. Puede ser simple como un error estándar o más complejo como entropía cruzada .

Llamamos a esta función de pérdida C y la denotamos de la siguiente manera:



Donde el costo puede ser igual al error estándar, la entropía cruzada o cualquier otra función de pérdida.

Basado en el valor de C, el modelo "sabe" cuánto deben ajustarse sus parámetros para acercarse al valor de salida esperado de y . Esto sucede usando el método de retropropagación.

Propagación inversa del error y cálculo de gradientes.

Basado en un artículo de 1989, el método de retropropagación:

Ajusta constantemente los pesos de las conexiones en la red para minimizar la medida de la diferencia entre el vector de salida real de la red y el vector de salida deseado .
y
... hace posible crear nuevas funciones útiles que distingan la propagación hacia atrás de métodos anteriores y más simples ...

En otras palabras, la propagación hacia atrás tiene como objetivo minimizar la función de pérdida ajustando los pesos y las compensaciones de la red. El grado de ajuste está determinado por los gradientes de la función de pérdida con respecto a estos parámetros.

Surge una pregunta: ¿Por qué calcular gradientes ?

Para responder a esta pregunta, primero debemos revisar algunos conceptos de computación:

El gradiente de la función C (x ¹ , x ² , ..., x ^m ) en x es el vector de derivadas parciales de C con respecto a x .



La derivada de la función C refleja la sensibilidad a un cambio en el valor de la función (valor de salida) en relación con el cambio en su argumento x ( valor de entrada ). En otras palabras, la derivada nos dice en qué dirección se mueve C.

El gradiente muestra cuánto es necesario cambiar el parámetro x (en la dirección positiva o negativa) para minimizar C.

Estos gradientes se calculan utilizando un método llamado regla de cadena.
Para un peso (w ^jk ) _{l, el} gradiente es:



(1) regla de la cadena
(2) Por definición, m es el número de neuronas por l - 1 capa
(3) Cálculo derivado
(4) valor final
Se puede aplicar un conjunto similar de ecuaciones a (b ^j ) _l :



(1) regla de la cadena
(2) Cálculo derivado
(3) Valor final
La parte común en ambas ecuaciones a menudo se denomina "gradiente local" y se expresa de la siguiente manera:



Un "gradiente local" se puede determinar fácilmente utilizando una regla de cadena. No pintaré este proceso ahora.

Los gradientes permiten optimizar los parámetros del modelo:

Hasta que se alcanza el criterio de detención, se realiza lo siguiente:



Algoritmo para optimizar pesos y compensaciones (también llamado descenso de gradiente)

• Los valores iniciales de w y b se seleccionan al azar.
• Epsilon (e) es la velocidad de aprendizaje. Determina el efecto del gradiente.
• w y b son representaciones matriciales de pesos y compensaciones.
• La derivada de C con respecto a w o b puede calcularse usando derivadas parciales de C con respecto a pesos o compensaciones individuales.
• La condición de terminación se cumple tan pronto como se minimiza la función de pérdida.

Quiero dedicar la parte final de esta sección a un ejemplo simple en el que calculamos el gradiente C con respecto a un peso (w ²² ) ₂ .

Acerquémonos al fondo de la red neuronal mencionada anteriormente:



Representación visual de la retropropagación en una red neuronal.
El peso (w ²² ) ₂ conecta (a ² ) ₂ y (z ² ) ₂ , por lo que calcular el gradiente requiere aplicar la regla de la cadena en (z ² ) ₃ y (a ² ) ₃ :



El cálculo del valor final de la derivada de C a partir de (a ² ) ₃ requiere el conocimiento de la función C. Dado que C depende de (a ² ) ₃ , el cálculo de la derivada debe ser simple.

Espero que este ejemplo haya logrado arrojar algo de luz sobre las matemáticas detrás del cálculo de gradientes. Si desea saber más, le recomiendo que consulte la serie de artículos de Stanford NLP, donde Richard Socher proporciona 4 excelentes explicaciones para la propagación hacia atrás.

Comentario final

En este artículo, expliqué en detalle cómo la retropropagación de un error funciona bajo el capó utilizando métodos matemáticos como el cálculo de gradientes, la regla de la cadena, etc. Conocer los mecanismos de este algoritmo fortalecerá su conocimiento de las redes neuronales y le permitirá sentirse cómodo cuando trabaje con modelos más complejos. ¡Buena suerte en tu viaje de aprendizaje profundo!

Eso es todo. Invitamos a todos a un seminario web gratuito sobre el tema "Árbol de segmentos: simple y rápido" .