Sol, viento y agua ver 0.2

Segunda temporada

Física de yates o yates para físicos.

Durante el entrenamiento en la escuela del timonel, los practicantes experimentados nos contaron cómo los verdaderos navegantes ven el viento "rosado", sienten el ángulo correcto en un lugar y no se ven afectados por el cretinismo espacial. Aparentemente, la educación en el campo de la física evita que una persona vea vientos "rosados" y hace que un lugar sea menos sensible. Trataré de descubrir cómo se mueve el yate en números.

¿Qué necesitas para digitalizar un yate?

1. Característica de remolque
   
2. Tabla de estabilidad
   
3. Vela geometría - medida en vivo
   la altura del ángulo superior de la gruta $$$h_ {gr superior} = 11.2 m$ ;
   altura del ángulo de tachuela de la gruta $$$h_ {gr hls} = 1,985 m$ ;
   ángulo de ovillo $$$h_ {gr pc} = 2.179 m$ ;
   distancia del ángulo de la vela mayor desde el mástil $$$l_ {gr pc} = 2.96 m$ ;
   altura del ángulo superior de la vela $$$h_ {st top} = 10 m$ ;
   Altura de la tachuela del apilador $$$h_ {st sls} = 1,111 m$ ;
   ángulo de ovillo $$$h_ {cst} = 1.5 m$ ;
   área de la gruta $$$S_ {gr} = 17.2 m ^ 2$ ;
   área de velas $$$S_ {st} = 14 m ^ 2$ ;
   área de vela lateral del casco $$$S_ {anf} = 7.315 m ^ 2$ ;
   área de viento frontal del casco $$$S_ {fr} = 3 m ^ 2$ ;
   proyección lateral del área del cuerpo submarino $$$S_ {dn} w = 1.82 m ^ 2$ ;
   área de quillas y madejas $$$S_ {ks} = 2,33 m ^ 2$ ;
   ángulo mínimo posible de la vela $$$\ psi_ {ct} = 18 ^ o$ .
   
   Tal vez tuve tanta mala suerte, pero ninguno de los fabricantes, durante mi búsqueda del yate, estuvo de acuerdo (no pudo) proporcionar estos datos para su yate. Estoy seguro de que el diseñador del yate tiene toda esta información, pero por alguna razón no puedo obtenerla. Lo minaré yo mismo.
   Ya he recibido la característica de remolque al digitalizar el yate en el programa de envío gratuito . Como recompensa por la perseverancia, el programa entrega inmediatamente un diagrama de estabilidad y un punto de centro de gravedad y un centro de arrastre lateral, y mucha otra información geométrica útil. El diagrama de estabilidad muestra la cantidad de torque que necesita aplicar al yate para depositarlo en cierto ángulo.
   
   
   
   

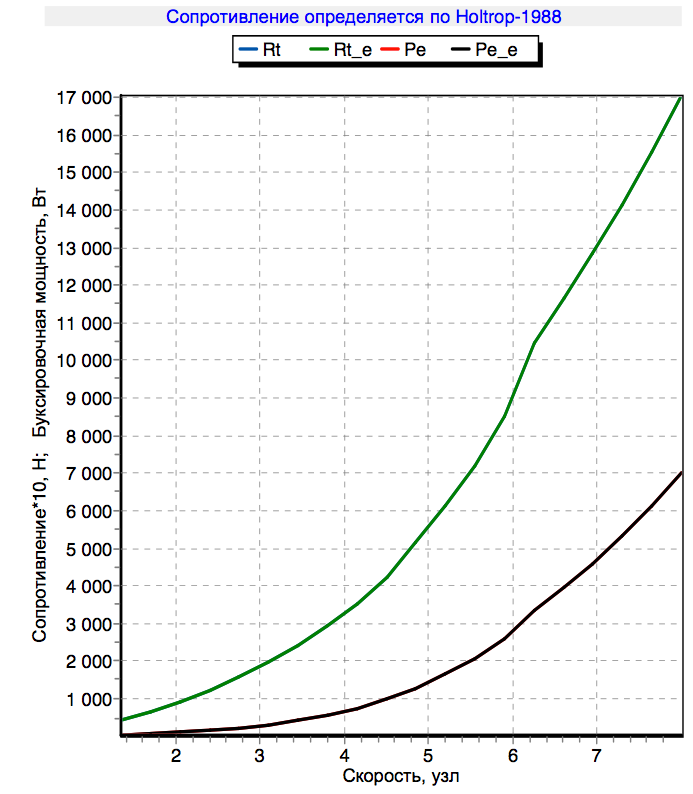
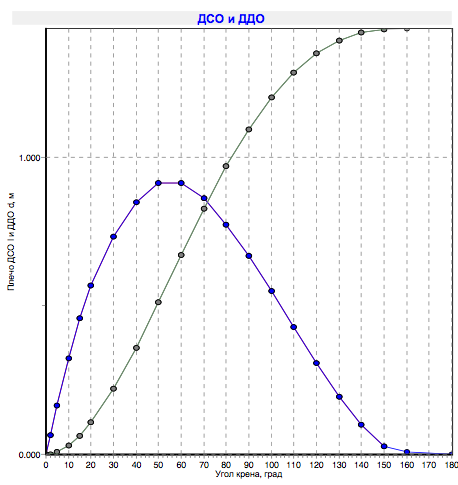
   Se recopilan todos los argumentos necesarios, procedamos a los cálculos.

   
   Obviamente, al avanzar, el yate supera la fuerza de resistencia del viento de frente. La velocidad del viento de frente es igual a la velocidad del yate, pero se dirige en sentido opuesto. Ya usé esta analogía al elegir un motor .
   

   $$

   $$R_ {fw} = 0.61 * S_ {fr} * v ^ 2, H,$$
   
   donde v es la velocidad del barco.
   
   Al mismo tiempo, la fuerza del viento real actúa sobre el yate. $$$F_ {rw}$ soplando en algún ángulo $$$\ alpha_ {rw}$ . Ambos vientos crean una fuerza igual a la suma vectorial de las fuerzas parciales. La llamada fuerza del viento del banderín: el viento que sopla a bordo del barco.
   
   El principal problema es la teoría de la relatividad. El observador (y todos los instrumentos de medición) está a bordo del yate y para él no hay forma de medir la fuerza y ​​la dirección del viento real, pero puede medir la dirección. $$$\ alpha_ {vw}$ y la velocidad del viento del banderín - $$$v_ {vw}$ así como la dirección $$$\ alpha$ medido por una brújula a bordo y la velocidad del barco - $$$v$ medido por un retraso a bordo (velocímetro).
   
   Encuentro los parámetros reales del viento basados ​​en mediciones de instrumentos a bordo.
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})}$ - velocidad real del viento;
   $$$\ alpha_ {rw} = \ pi-arccos (\ frac {v_ {rw} ^ 2 + v ^ 2-v_ {vw} ^ 2} {2 * v * v_ {rw}})$ - el ángulo del viento real pospuesto desde la dirección "hacia adelante".
   
   
   
   Para pequeños pokatushek todo esto no tiene sentido. La conexión entre los vientos reales y pendientes es necesaria para planificar viajes lo suficientemente largos (cuando el objetivo no está en línea directa de visión). Después de todo, la planificación se lleva a cabo en un mapa del planeta con la indicación de vientos reales (de acuerdo con las previsiones meteorológicas), y el movimiento del yate proviene de un viento pendular.
   
   Ahora que se ha establecido la conexión con la realidad, es hora de descubrir cómo surge la fuerza impulsora. Está claro que el viento llena las velas y el bote corre a lo largo de las olas.
   
   De hecho, una vela en un yate opera en dos modos principales:
   
   
   1. modo de ala aerodinámica: utilizado en vientos en contra,
      
   2. Modo de freno aerodinámico: utilizado en vientos suaves.
      
   
   El perfil de la vela está cosido de tal manera que, al estar lleno de viento de frente, toma la forma de un ala. Es decir, hay un ala que se mueve a cierta velocidad en relación con el aire; por lo tanto, surge una fuerza de elevación en él $$$F_ {aire}$ . Por analogía con el ala de un avión, intentaré simplificar su tamaño y dirección en relación con el yate.
   
   Para que la vela tome su forma de trabajo, es necesario girarla un poco en relación con la dirección del viento. El ángulo de rotación se llama "ángulo de ataque" $$$\ alpha_ {a}$ . Para simplificar los cálculos, el ala se compara con una placa plana, y las diferencias se presentan en forma de una tabla de coeficientes aerodinámicos , donde Su es el coeficiente de diferencia de elevación y Cx es el coeficiente de diferencia de resistencia. La fuerza de elevación se dirige perpendicular a la placa, y la fuerza de resistencia es paralela. La geometría de la placa está determinada por el coeficiente de alargamiento aerodinámico. $$$A_ {y} = h ^ 2 / S$ donde h es la altura de la vela; S es el área de la vela.
   
   

   pero	Cy; Ay = 6	Cx	Cy; Ay = 3	Cx
   0 0	0 0	0,09	0 0	0,09
   5 5	0,83	0.1	0,65	0.1
   10	1.19	0,15	0.9	0,15
   15	1,22	0,3	1,1	0.25
   20	1.14	0.4 0.4	1,18	0.4 0.4
   25	1.06	0,485	1,2	0.5 0.5
   30	0,98	0,57	1	0,55
   40	0.9	0,73	0,82	0,65
   45	0,75	0,88	0.7	0,85
   50	0.6	1	0.6	1
   70	0.2 0.2	1,15	0.2 0.2	1,15
   90	0 0	1,2	0 0	1,2

   
   El ala, en contraste con la placa, es una estructura tridimensional, por lo tanto, una tabla separada muestra cómo el tamaño de la protuberancia del "vientre" afecta los coeficientes de diferencia de la placa.
   

   panza	Su3	Cx3
   0,0667	-0,2	0.1
   0.1	0 0	0 0
   0.2 0.2	0 0	0.1
   0.25	0.1	0.2 0.2

   
   Proyección de fuerza de vela $$$F_ {aire}$ a la dirección longitudinal del yate - potencia útil:
   $$$F_ {s} = 0.61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * sin (\ alpha_ {vw}) - (Cx + Cx3) * cos (\ alpha_ {vw})) $$ .
   Proyección de fuerza de vela $$$F_ {aire}$ en la dirección transversal del yate - fuerza de deriva:
   $$$F_ {d} = 0.61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * cos (\ alpha_ {vw}) - (Cx + Cx3) * sin (\ alpha_ {vw})) $$ .
   
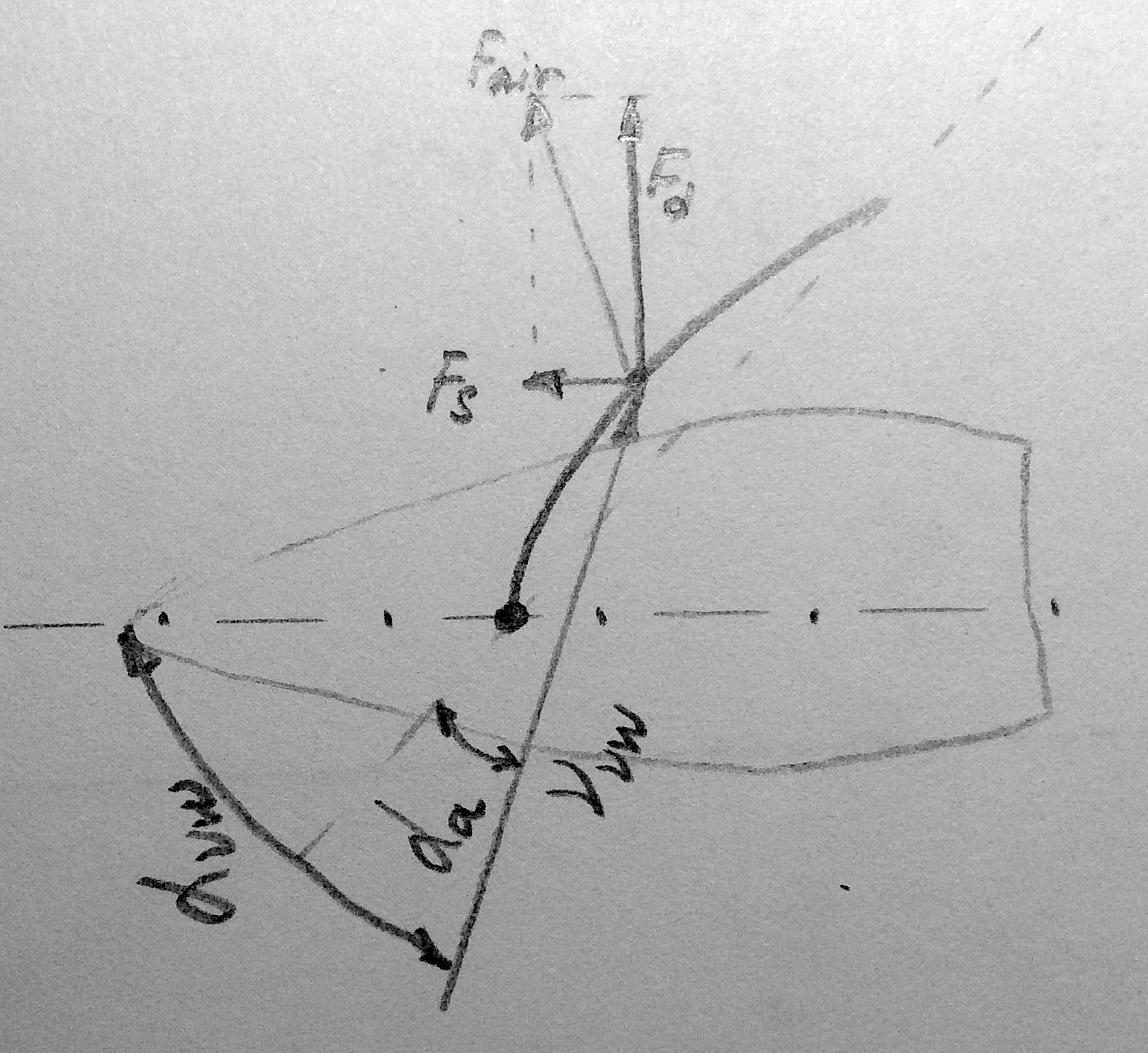
   La fuerza de la resistencia al viento del casco ralentizará el movimiento:
   $$$R_ {fw} = 0.61 * S_ {fr} * v_ {vw} ^ 2 * sin (\ alpha_ {vw})$
   Habiendo recibido la proyección de fuerzas, puedo encontrar los vectores de velocidad longitudinal y transversal del yate. Componente longitudinal de velocidad $$$v_ {dp}$ Encuentro la característica de remolque según el horario.
   Con el componente transversal, todo es más complicado.
   Primero necesitas encontrar la altura del centro de la vela. Una vela es un triángulo en el que un lado es un arco convexo. Lo presentaré como dos velas: una pieza triangular y otra en forma de hoz. El área del triángulo se calcula como la mitad del producto del ancho por la altura, y el área de la "hoz" es la diferencia entre el área de la vela y el área del triángulo.
   

   $$

   $$S = (h_ {gr top} -h_ {gr hls}) * l_ {gr sht} / 2,$$
   donde $$$S_ {hoz} = S_ {gr} -S$
   Altura del centro de la vela:
   

   $$

   $$h_ {gr cp} = \ frac {h_ {gr \ Delta cp} * S \ Delta + ((h_ {gr top} -h_ {gr pc}) * S_ {sickle} / 1,8)} {S_ {gr }},$$
   donde $$$h_ {gr \ Delta cp} = h_ {gr pc} + (h_ {gr top} + h_ {gr hl} -2 * h_ {gr pc}) / 3,$ La altura del centro de la vela vela triángulo sin hoz.
   Por lo general, un yate tiene dos velas: la principal es la vela mayor y la delantera es la vela de vela. La vela de estambre generalmente se realiza sin hoz y luego su altura del centro de la vela:
   

   $$

   $$h_ {st \ Delta cp} = h_ {st st} + (h_ {st top} + h_ {st hls} -2 * h_ {st sht}) / 3$$
   
   Centro de navegación total:
   

   $$

   $$h _ {\ Sigma cpu} = \ frac {h_ {gr cp} * S_ {gr} + h_ {ct \ Delta cp} * S_ {ct}} {S_ {gr} + S_ {ct}}$$
   
   Ahora puedo determinar el momento de inclinación que actúa en el yate:
   

   $$

   $$M_ {kr} = F_ {d} * h _ {\ Sigma cp}.$$
   
   Del diagrama de estabilidad encuentro el ángulo del yate. $$$\ phi$ .
   Expreso la fuerza de la deriva del yate:
   

   $$

   $$R_ {d} = 9.8 * 102 * (S_ {ks} * atan (\ frac {v_ {d}} {v_ {dp}}) * v_ {dp} ^ 2 * (cos (\ phi- \ gamma) -cos (\ phi + \ gamma)) * 0.96+ (S_ {ks} + S_ {dp w}) * 1.15 * v_ {d} ^ 2 * cos (\ phi- \ gamma)), $$$
   donde está el ángulo de las quillas del yate de dos quillas en relación con la vertical.
   La fuerza de la presión del viento sobre el cuerpo da una deriva adicional.
   

   $$

   $$F_ {anf} = 0.61 * v_ {d} ^ 2 * S_ {anf} * cos (\ alpha_ {vw}).$$
   
   Velocidad $$$v_ {d}$ es una sustitución de media división hasta un equilibrio de fuerzas $$$F_ {d} + F_ {anf} = R_ {d}$ .
   Ahora es obvio que el yate se mueve "oblicuamente", es decir tiene velocidad de movimiento transversal y longitudinal. Esto trae otra sorpresa. Dirección - $$$\ alpha$ medido por una brújula a bordo y la velocidad del barco - $$$v = v_ {dp}$ medido por el retraso a bordo (velocímetro) muestra solo el componente longitudinal.
   Es necesario unir dimensiones a la realidad. El ángulo real de la nave. $$$\ alpha_ {real}$ llamado el "ángulo de seguimiento":
   

   $$

   $$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha$$
   
   y puede diferir de la medida por 10-20 grados.
   La velocidad real del yate puede determinarse mediante el teorema de Pitágoras:
   

   $$

   $$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}.$$
   
   
   En conclusión, daré un ejemplo de cálculo para mi barco de la situación más interesante: el movimiento contra el viento. Está claro que no irás estrictamente contra el viento debajo de las velas, pero en algún ángulo agudo puedes hacerlo.
   
   Debe comenzar con la vela delantera: la barra de suspensión se monta en la parte superior del mástil, el ángulo frontal de la proa del yate y la parte posterior con una sábana (cable blando) a través del rodillo hasta el cabrestante. Su tensión regula el ángulo de la vela en relación con el yate. Ángulo de instalación mínimo $$$\ psi_ {st min} = 18 ^ o$ obtenido a la tensión máxima de la lámina. Extensión aerodinámica de la vela. $$$A_ {y st} = h_ {st} ^ 2 / S_ {st} = $ 5.$ . Usando el método de interpolación lineal encuentro el ángulo óptimo de ataque $$$\ alpha_ {a} = 10 ^ o$ de la tabla de coeficientes aerodinámicos. Criterio de Optimidad - Maximización $$$F_ {s st}$ en donde Su = 1.17; Cx = 0.15. La vela permanentemente instalada de esta manera funcionará efectivamente en la dirección del viento del banderín. $$$\ alpha_ {vw} = \ psi_ {ct} + \ alpha_ {a} = 18 + 10 = 28 ^ o$ . Buen clima para caminar y navegar cuando la velocidad del viento es de alrededor de 5-7 m / s. Por la belleza de los números, tomaré $$$v_ {vw} = 6.55 m / s$ .
   
   La proyección de la fuerza de la vela en la dirección longitudinal del yate es una fuerza útil:
   

   $$

   $$F_ {s st} = 0.61 * 6.55 ^ 2 * 14 * ((1.17 + 0) * sin (28 * \ pi / 180) - (0.15 + 0) * cos (28 * \ pi / 180)) = 153.5 H$$
   
   La proyección de la fuerza de la vela en la dirección transversal del yate: la fuerza de deriva:
   

   $$

   $$F_ {d st} = 0.61 * 6.55 ^ 2 * 14 * ((1.17 + 0) * cos (28 * \ pi / 180) - (0.15 + 0) * sin (28 * \ pi / 180)) = 405.8 H$$
   
   La resistencia al viento del casco evita el movimiento hacia adelante.
   

   $$

   $$R_ {fr w} = 0.61 * 6.55 ^ 2 * 3 * cos (28 * \ pi / 180) = 69 H$$
   
   Según la característica de remolque, determinamos la velocidad $$$v_ {dp} = $ 2.7$ nodo = 1.4 m / s
   

   $$

   $$h_ {st \ Delta cp} = 1.5 + (10 + 1.5-2 * 1.1) / 3 = 4.6 m$$
   
   $$$M_ {kr st} = 405.8 * 4.6 = 1867 N / m$ , del diagrama de estabilidad encontramos el ángulo del talón $$$\ phi_ {ct} = 3.9 ^ o$ . Bueno, estas son insignificantes, por lo tanto, agregaremos una vela más: ¡la vela mayor!
   La vela mayor funciona como una aleta en el ala de un avión y gira alrededor del mástil en ángulo $$$70 ^ o$ . El coeficiente de alargamiento aerodinámico de la vela mayor. $$$A_ {y gr} = h_ {gr} ^ 2 / S_ {gr} = $ 4.$ ;
   ángulo de ataque óptimo $$$\ alpha_ {a} = 10 ^ o$ ; Su = 1.09; Cx = 0.15.
   La proyección de la fuerza de la gruta en la dirección longitudinal del yate es una fuerza útil:
   

   $$

   $$F_ {s gr} = 0.61 * 6.55 ^ 2 * 17.2 * ((1.09 + 0) * sin (28 * \ pi / 180) - (0.15 + 0) * cos ( 28 * \ pi / 180)) = 170 H$$
   
   La proyección de la fuerza de la gruta en la dirección transversal del yate es la fuerza de deriva:
   

   $$

   $$F_ {d gr} = 0.61 * 6.55 ^ 2 * 17.2 * ((1.09 + 0) * cos (28 * \ pi / 180) - (0.15 + 0) * sin ( 28 * \ pi / 180))) = 464 H$$
   
   $$$h _ {\ Sigma cpu} = 4.16 m$ , $$$M_ {kr} = 3127 H$ y ángulo de balanceo $$$\ phi _ {\ Sigma} = 8.5 ^ o$ .
   Fuerza de avance total:
   $$$F_ {s} = F_ {s st} + F_ {s gr} -R_ {fr w} = 153.5 + 170-69 = 254 H$ velocidad de avance $$$v_ {dp} = $ 3.$ nodo o 1,86 m / s.
   Si suponemos que el viento real sopla estrictamente hacia el norte, entonces la brújula a bordo mostrará el ángulo del componente longitudinal de la velocidad del yate $$$\ alpha_ {vw} = 38.1 ^ o$ .
   La velocidad de deriva será $$$v_ {d} = 0.418 m / s$ .
   Ahora necesitamos llevar estos resultados a la realidad.
   
   El ángulo de seguimiento del movimiento real será:
   $$$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha = atan (\ frac {0.418} {1.86}) + 38.1 = 51 ^ o$ , este es el ángulo del viento real $$$\ alpha_ {rw}$ al vector de movimiento del yate.
   
   Y la velocidad real del movimiento en el espacio: $$$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}$ = 1.92 + 0.4182 = 1.9 m / s.
   Velocidad real del viento:
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})} = 5 m / s$ .
   En tales condiciones, la velocidad de avance estrictamente contra el viento será de 1.2 m / so 2.35 nudos, y tendrá que moverse a lo largo de un camino en zigzag - tachuelas.
   
   Después de calcular otros posibles ángulos del viento del banderín, puede obtener un diagrama circular de la dependencia de la velocidad real del yate del viento real. 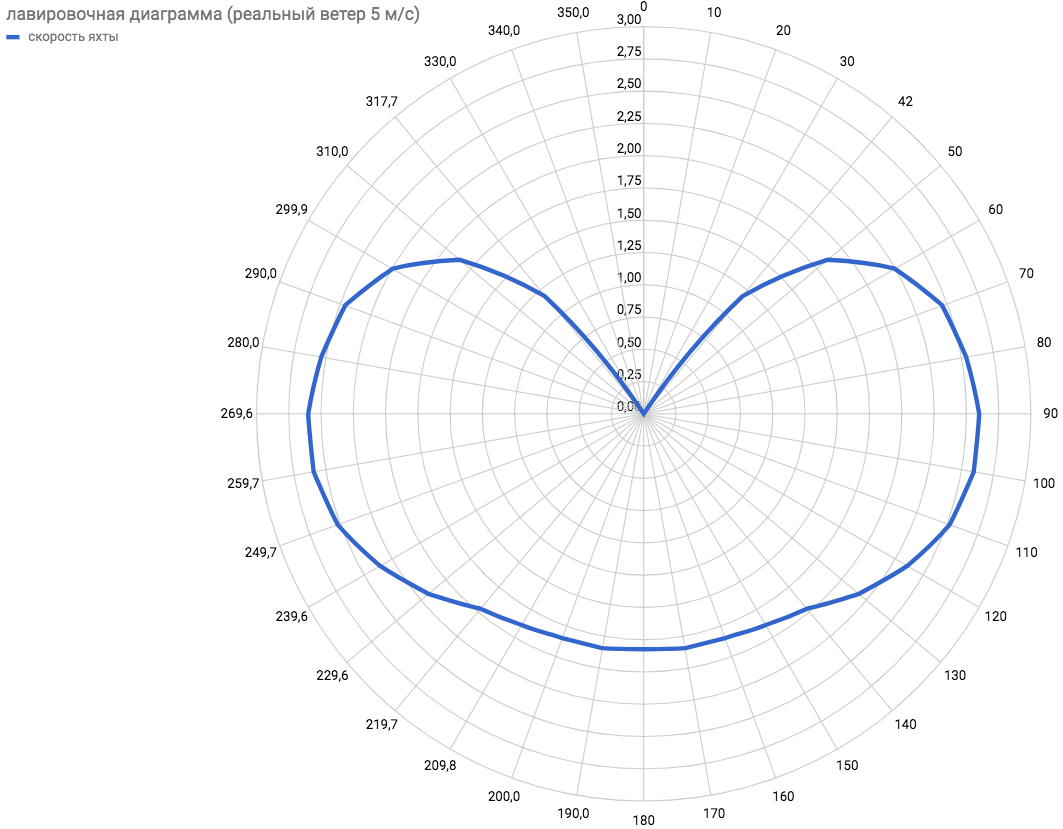Al usarlo, ya puede planificar rutas en el mapa de acuerdo con el pronóstico del viento. Además, quedó claro que el ángulo mínimo posible $$$\ alpha_ {min real} = 43.5 ^ o$ , y la velocidad máxima contra el viento se logra con el ángulo de rumbo $$$50 ^ o <\ alpha_ {real} <53 ^ o$ para viento 5 m / s.