🧝🏽 🍻 😳 Visualización de los límites de una solución clasificadora basada en imágenes. 👩🏻‍🎤 🧖🏼 🔅

Introduccion

Comprender cómo el clasificador descompone el espacio inicial multidimensional de los atributos en muchas clases objetivo es un paso importante para analizar cualquier problema de clasificación y evaluar la solución obtenida mediante el aprendizaje automático.

Los enfoques modernos para visualizar las decisiones de los clasificadores usan principalmente diagramas de dispersión que solo pueden mostrar proyecciones de las muestras de entrenamiento originales, pero no muestran explícitamente los límites reales de la toma de decisiones, o usan un dispositivo clasificador interno (por ejemplo, kNN, SVM, Regresión logística) para el cual es fácil construir una geometría interpretación Este método no es adecuado para la visualización, por ejemplo, de un clasificador de red neuronal.

El artículo "Visualización basada en imágenes de los límites de decisión del clasificador" (Rodrigues et al., 2018) propone un método alternativo eficaz, hermoso y bastante simple para visualizar las soluciones del clasificador, que carece de las desventajas anteriores. A saber, el método es adecuado para clasificadores de cualquier tipo y construye los límites de la toma de decisiones utilizando imágenes con una frecuencia de muestreo arbitraria.

Esta publicación es una breve descripción de las principales ideas y resultados del artículo original.

Descripción del método

La base del método es el muestreo inverso (ing. Upsampling) desde el plano de la imagen $\ mathbb {R} ^ 2$ que está representado por un conjunto de píxeles en el espacio de características $\ mathbb {R} ^ n$ .

El método requiere dos asignaciones $P: \ mathbb {R} ^ n \ to \ mathbb {R} ^ 2$ - proyección directa del espacio de características al plano de la imagen y al inverso $P ^ {- 1}: \ mathbb {R} ^ 2 \ to \ mathbb {R} ^ n$ . Como tales mapeos, se utilizan LAMP (Joia et al. 2011) e iLAMP (Amorim et al. 2012) , respectivamente.

Edificio

Para construir una imagen, debe asignar un color a cada píxel. Para esto, para cada píxel encontrará $N \ geq 1$ puntos del hiperespacio fuente donde - un parámetro especificado por el usuario. Deja que el píxel ya tiene $n (y) \ geq 0$ prototipos reales del conjunto de entrenamiento. Entonces elige uniformemente $\ max (N - n (y), 0)$ los puntos restantes de la superficie del píxel y encuentre el prototipo para ellos a través de la proyección posterior $x_i = P ^ {- 1} (y_i)$ . Por lo tanto, el color de cada píxel estará determinado por al menos puntos del espacio fuente, y se pintará toda la imagen.

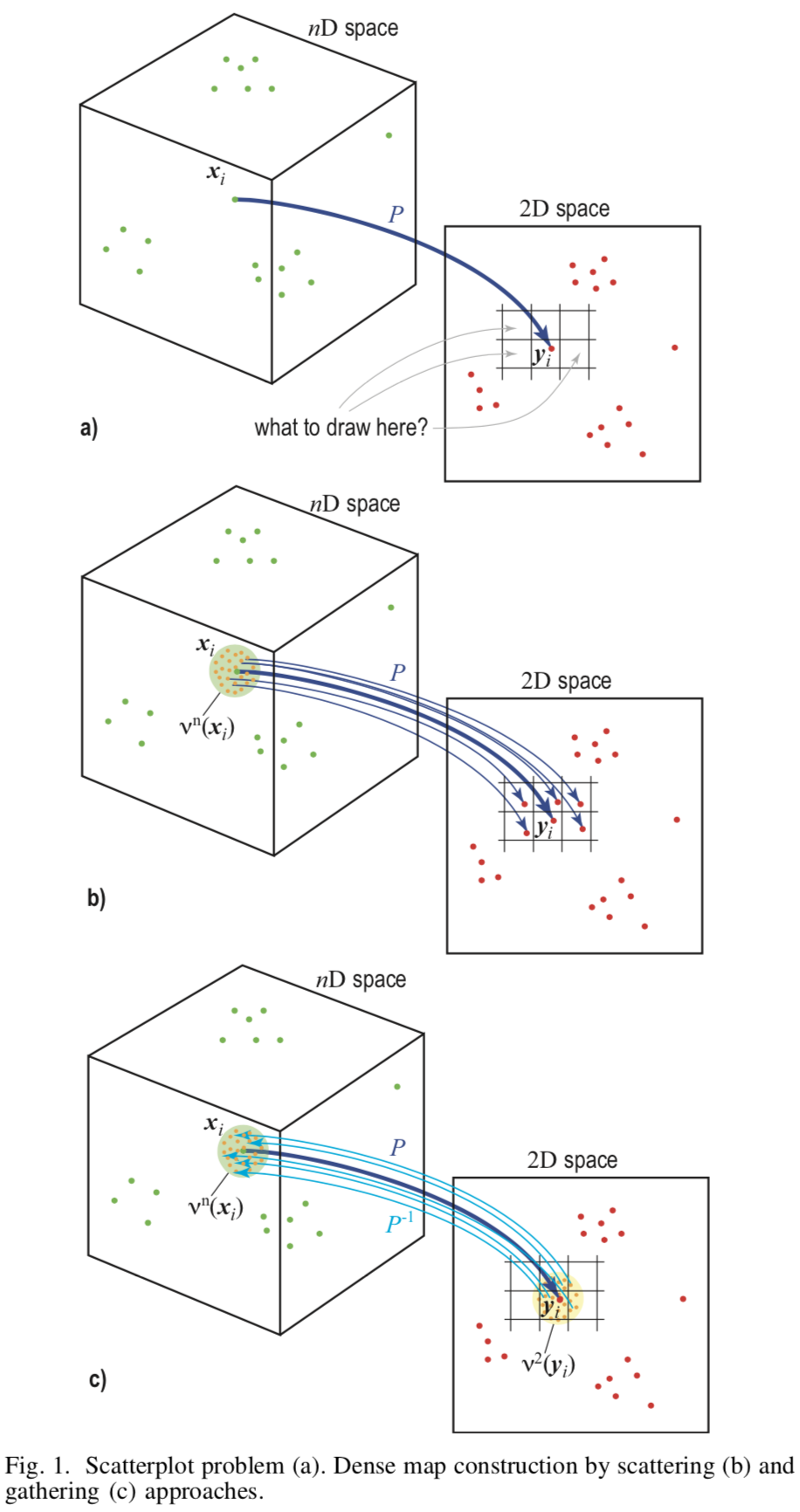
Diferencia de métodos
[Fig.1] Ilustración esquemática de diferentes enfoques

Definición de color

Color cada píxel determinado por un voto mayoritario para las etiquetas de clase de las preimágenes correspondientes.

$d (y) = \ text {argmax} _ {k \ in C} \ sum_ {y_i \ in y} [f (P ^ {- 1} (y_i)) = k]$

donde - muchas de todas las clases, $f: \ mathbb {R} ^ n \ a C$ - clasificador.

A cada clase se le asignará un tono (ing. Hue) H_T (k) - si la proyección tiene puntos de la muestra real y un tono ligeramente cambiado $H _ {\ text {synth}} (k)$ para píxeles en los que solo hay puntos sintéticos.

Confusión

Definir la mezcla de píxeles (de confusión en inglés) c (y) - como la relación entre el número de etiquetas de la clase predominante y el número total de imágenes inversas de píxeles :

$c (y) = \ frac {\ max_ {k \ in C} \ sum_ {y_i \ in y} [f (P ^ {- 1} (y_i)) = k]} {| y |}$

Alto valor c (y) indica la consistencia del clasificador, mientras que un valor bajo indica un acercamiento al límite divisorio. Combinar información codificada en saturación de píxeles S (y) - cuanto mayor es la consistencia, mayor es la saturación.

Densidad

Aunque se ha generado un mínimo puntos de preimagen para cada píxel, puede haber píxeles para los que hay muchos más puntos reales del conjunto de entrenamiento. Dichos píxeles deben considerarse al renderizar. Para hacer esto, ingrese la densidad de píxeles $\ rho (y)$ como el número de sus puntos de imagen inversa de $\ mathbb {R} ^ n$ . Se podría usar esta densidad directamente para determinar el brillo de un píxel como $V (y) = \ frac {\ rho (y)} {\ rho_ {max}}$ , pero los autores del artículo señalan que esto no da el resultado deseado, porque algunos tonos son obviamente más oscuros que otros. Por lo tanto, se utiliza un ajuste más complicado al mismo tiempo de saturación y brillo a través de un parámetro de densidad normalizado.

$\ hat {\ rho} = max (\ frac {1} {20} \ frac {\ rho} {\ rho_ {avg}}, 1)$

Entonces si $\ hat {\ rho} \ en [0, 0.5]$ - el brillo depende linealmente del parámetro dentro $[V_ {min} = 0.1, V_ {max} = 1]$ . En $\ hat {\ rho} \ en [0.5, 1]$ comienza a crecer linealmente la saturación de $S_ {min} = 0.2$ antes $S_ {max} = 1$ .

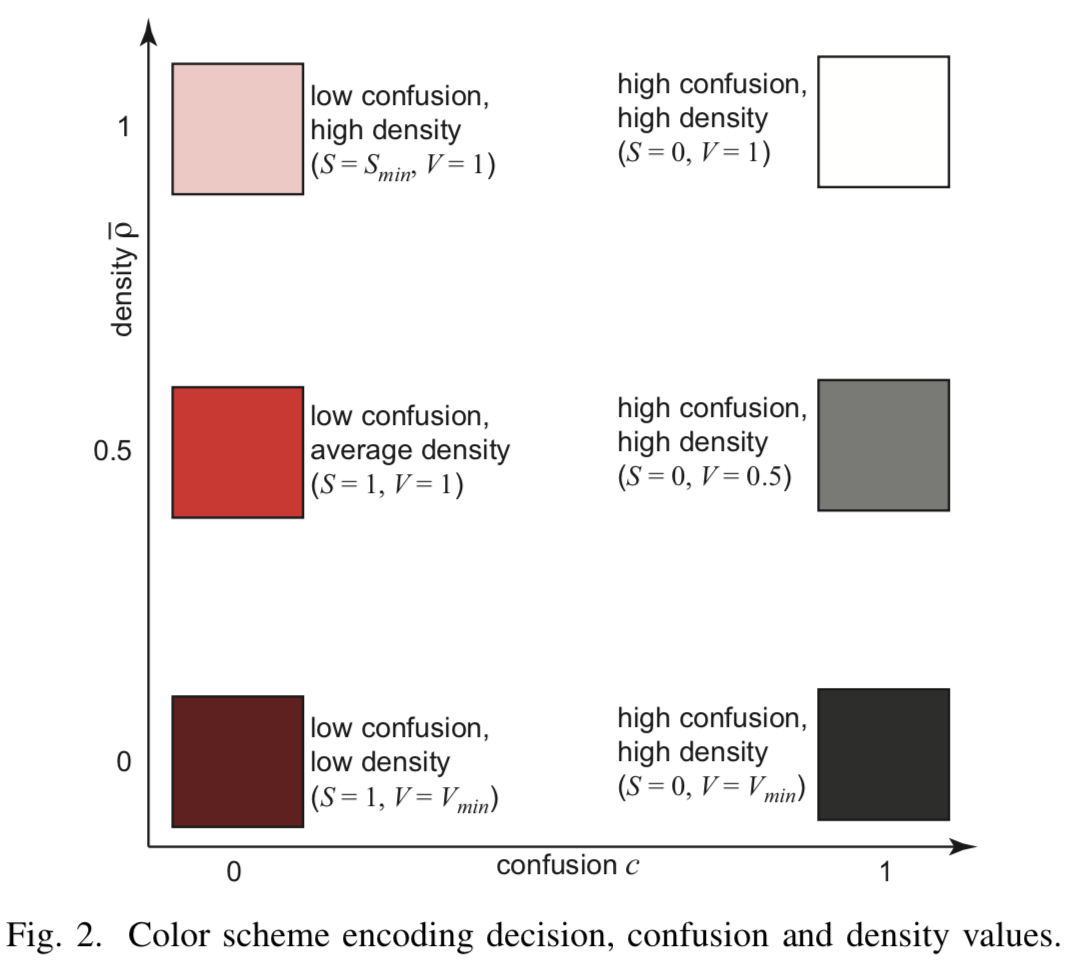
[Fig.2] Codificación de colores

Experimentos y resultados

Para los experimentos, se resolvieron los problemas de clasificación binaria en el conjunto de imágenes digitales MNIST y clasificación multiclase en el conjunto de datos de segmentación de imágenes , que contiene 2310 imágenes divididas en 7 clases. Hay 19 atributos para cada imagen.

Resultados de imágenes con varias configuraciones de resolución y el número mínimo de prototipos para el clasificador binario LogisticRegression en MNIST se muestran en la figura [3]. Las clases están separadas por una línea recta con alta precisión y el algoritmo de visualización hace un excelente trabajo. Con una resolución creciente, las nubes de los puntos fuente se disuelven casi por completo entre los muchos puntos generados.

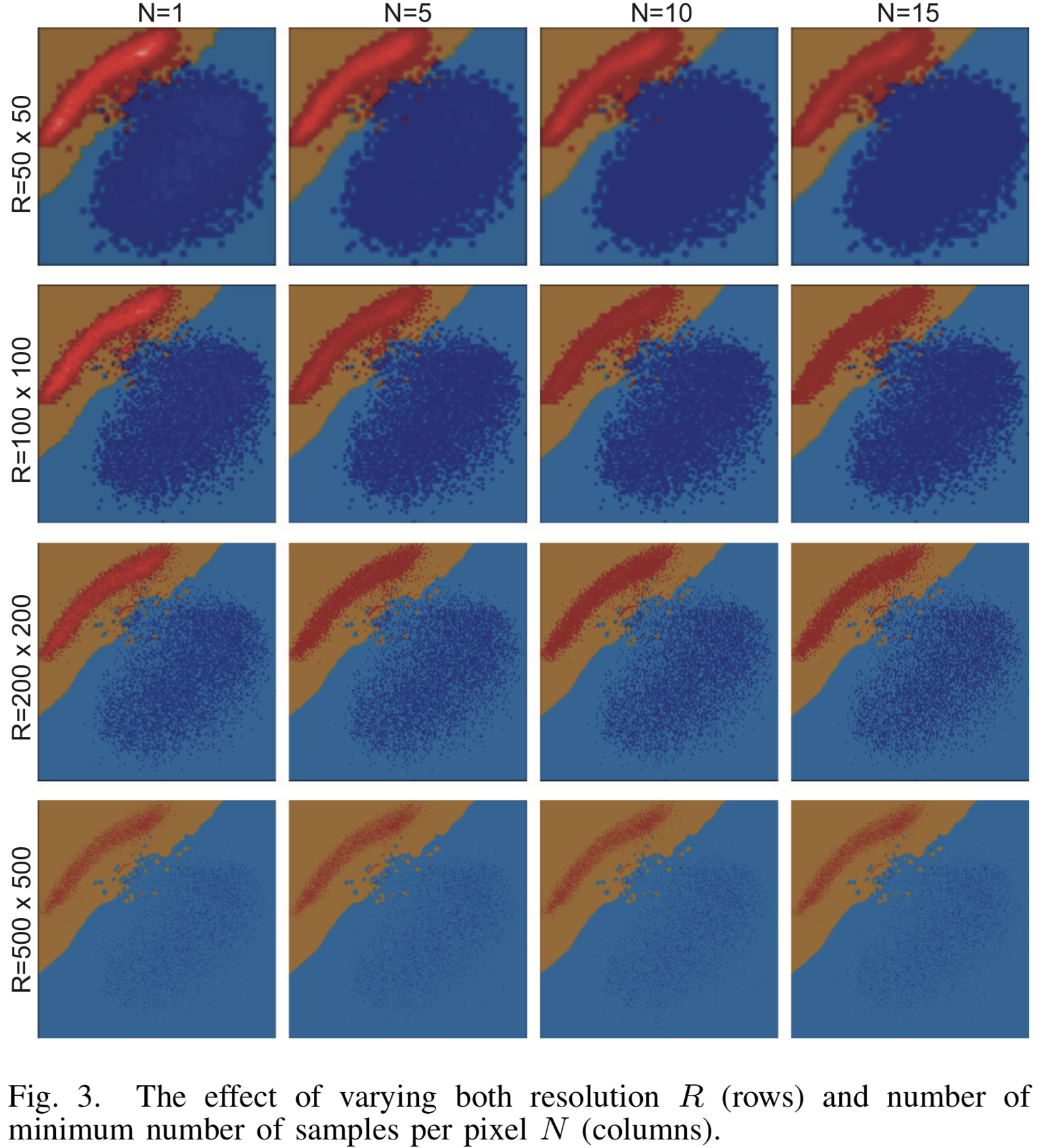
Codificación de color
[Fig. 3] El resultado de visualización para varios parámetros de resolución y el número mínimo de muestras N para el clasificador LogisticRegression

Visualización cuando $R = 500 \ text {x} 500, N = 5$ para tres clasificadores diferentes para la clasificación múltiple en la figura [4]. Las proyecciones de los puntos de partida son muy variadas y no es posible construir límites divisorios explícitos en los lugares donde se acumulan las proyecciones de los casos de prueba. Sin embargo, aparte del grupo principal, se obtuvieron límites de clase explícitos, cuya información no se muestra en proyecciones ordinarias, sino que se obtiene solo con la ayuda de puntos sintéticos.

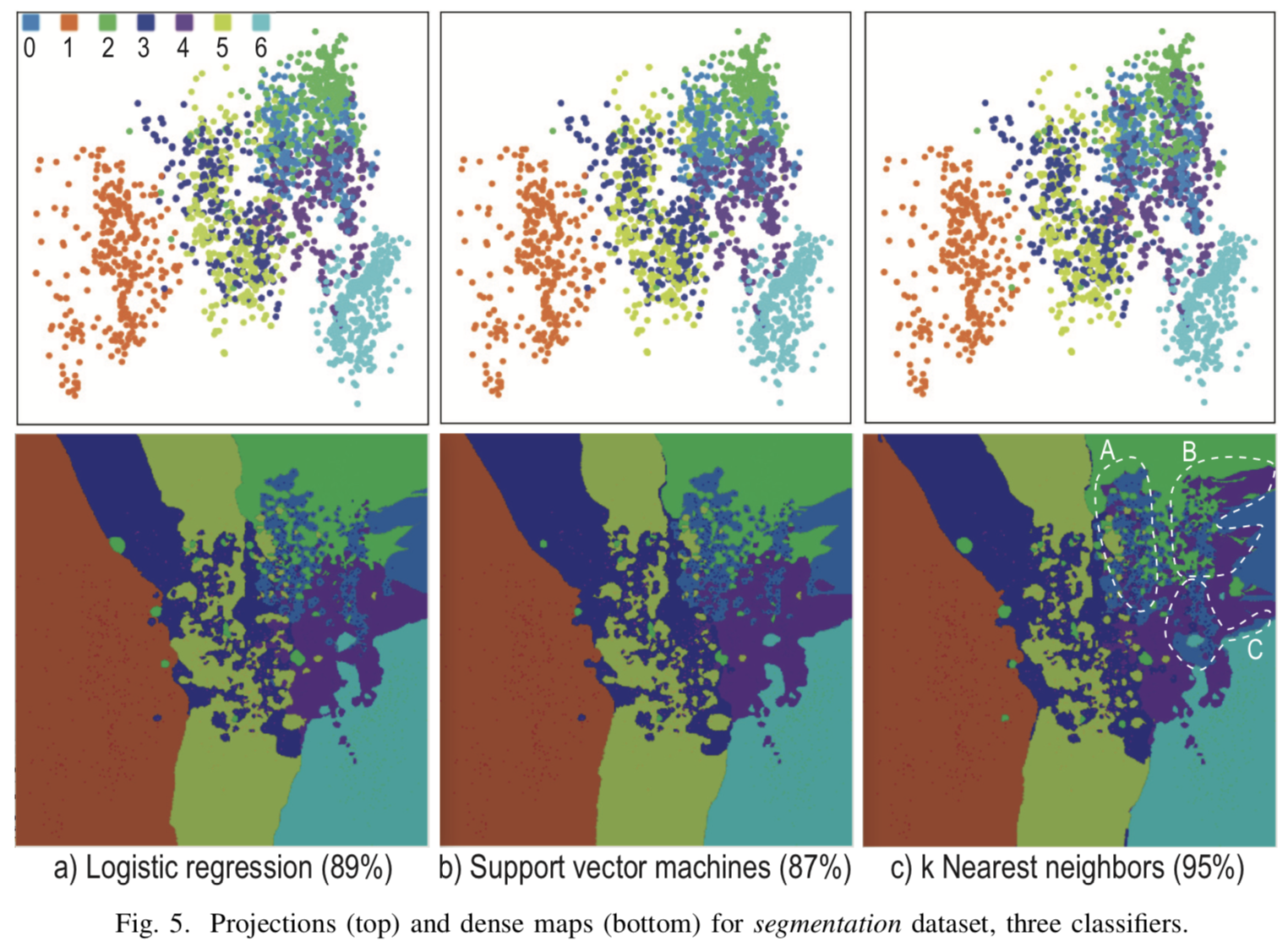
Codificación de color
[Fig. 4] El resultado de la visualización de tres clasificadores diferentes para k = 7, R = 500x500, N = 5

Conclusión

La visualización de los límites de clase se puede utilizar en la construcción y depuración de un algoritmo decisivo, en la selección de hiperparámetros, en la lucha contra el reciclaje, para presentar y analizar los resultados.

El método descrito por los autores del artículo original se puede utilizar para cualquier problema de clasificación, donde los datos se pueden representar como un conjunto de signos de una dimensión fija. A diferencia de otros algoritmos de visualización, este enfoque se puede usar para cualquier clasificador arbitrariamente complejo y para conjuntos de datos con un número arbitrario de ejemplos, incluso con uno muy pequeño, porque incluso con pequeños El algoritmo funciona de manera estable, sin perder mucha calidad.

Visualización de los límites de una solución clasificadora basada en imágenes.