¿Es un autómata un evento?

1. Introducción

Habiendo escuchado de labios autoritarios que “los autómatas son una cosa de eventos” [3], me di cuenta de que los autómatas finitos están marcados completamente. Juzgue usted mismo: en la biblioteca Qt, se implementa un modelo de evento de autómatas [1], en UML también lo son [2], observamos los autómatas del paquete de extensión Simulink-Stateflow del sistema MATLAB [4] (en adelante simplemente Stateflow) y allí sobre eventos, etc. etc. En este contexto, la declaración de Ph.D. A.A. Es malo interpretar de otra manera, porque nada más puede ser, porque no puede ser.

Pero, si recuerdas la teoría de los autómatas finitos (TCA), ¡no hay una palabra sobre autómatas de eventos en ella! Pero para contradecir la teoría, se necesitan argumentos importantes. ¿Hay alguna razón para dudar de la profesionalidad de D. Harell, como creador de la notación en la que el lenguaje UML, el paquete Stateflow, basa sus ideas, que, a su vez, no son desconocidas para A.A. Travieso? De hecho, existen UML, Stateflow, programación SWITCH y otras opciones de programación automática y, en un grado u otro, funcionan con éxito.

Entonces, ¿es posible eliminar el "estigma de los eventos" del modelo de máquina de estados finitos separando las "chuletas de las moscas"? Es decir separe la teoría de autómatas y modelos computacionales similares a los modelos de D. Harel. Y considerar que este último, aunque utiliza la terminología de la teoría de autómatas, representa, a juzgar por su implementación, el desarrollo de un modelo de diagramas de bloques de programas.

Observación 1. En este caso, estamos hablando del modelo de gestión del programa, y ​​no del modelo del programa en sí (para más detalles sobre los modelos, consulte [5]).

Entonces, recuerde, la biblioteca Qt implementa un modelo de eventos de una máquina de estados finitos, que fue prestada de UML. Stateflow implementa el mismo modelo. Es decir La fuente de los eventos es UML, donde los autómatas se basan en la notación propuesta por D. Harel. Pero culpar a este último por crear tal programación automática tampoco sería cierto, porque El “acontecimiento” es una tendencia de los enfoques modernos para la implementación de modelos de software. Se basa en opiniones autorizadas, como las mencionadas "las máquinas son una cosa de eventos", y la gran popularidad de los lenguajes y tecnologías como UML. Sin duda, este es el resultado de la imitación de máquinas bajo los principios existentes de operación de sistemas operativos.

Pero, repetimos, ya que no parece extraño, pero para algunos incluso puede convertirse en noticia, en la teoría de autómatas no existe un modelo de evento de un autómata finito. Al menos en esa parte que se considera clásica (ver para más detalles, por ejemplo, [6] o [7]). Existe una clara contradicción entre teoría y práctica. En tal situación, debe hacer algo con la teoría o influir de alguna manera en la práctica. Pero, tal vez, ¿los programadores tienen razón en su deseo de finalizar el modelo de una máquina de estados finitos al incluir el concepto de "evento" en él [8, 9]?

Pero cómo conectar los deseos de los programadores con el hecho de que "las mayores dificultades en el uso del enfoque de autómatas están relacionadas con la comprensión de las características del funcionamiento de los autómatas en los sistemas de eventos" (ver [8]). Me gustaría entender las causas de tales problemas y, en este contexto, implementar máquinas de eventos y / o sus análogos. Para este propósito, por detalles, tomamos la implementación de autómatas en Qt y los repetimos utilizando el modelo de un autómata finito clásico.

Dicha implementación de los autómatas de eventos es necesaria para evaluar y / o superar las "características" mencionadas. El uso del modelo clásico extenderá la teoría de los autómatas a la práctica de la "programación de eventos" también. Y, al final, un análogo basado en otro modelo solo expandirá el área de aplicación de los modelos de máquinas de estados finitos.

2. Eventos, señales e identidad de género de los autómatas.

En UML, un evento es "un fenómeno significativo que tiene una cierta posición en el tiempo y el espacio ... y conlleva ciertas consecuencias" [10]. Un evento en la teoría de autómatas es un subconjunto de los caracteres de entrada representados por los caracteres del alfabeto de salida (incluso existe el concepto de álgebra de eventos en el TCA) [6]. Lo mismo que causa la transición de un autómata se llama señales de entrada en la teoría de autómatas. Son las consecuencias y “la razón, la transición del autómata de un estado a otro. En este caso, las señales de salida son la "respuesta del autómata a las señales de entrada". Ambas "se refieren a instantes de tiempo determinados por las correspondientes transiciones del autómata" [6]. En UML, la señal (señal) es "una entidad con nombre que sirve como medio de comunicación entre objetos "[10].

Por lo tanto, los nombres de los términos son los mismos, pero el significado invertido en ellos es diferente. Aunque, si los reorganiza, puede encontrar una similitud: queda claro que los eventos en UML corresponden a las señales de las máquinas de estados finitos en el TCA. Pero, tal vez, ¿diferentes entidades también están ocultas bajo el término "máquina de estados finitos"? Tratemos de resolverlo, comenzando con los eventos ...

El autómata de eventos es un autómata pasivo, porque funciona solo en el momento de la llegada de los eventos. En contraste, el autómata clásico representa el modelo activo. Funciona sin referencia a nada (para más detalles sobre autómatas pasivos y activos, consulte [9]). Aquí comienza la asociación con dos corredores, donde el primero es impulsado por patadas (eventos) y el segundo corre por sí mismo.

En contraste con [8], al principio no asociaremos los momentos de ocurrencia de eventos con el inicio del autómata. Por lo tanto, nos mantendremos en el marco de la teoría de los autómatas, que determina la naturaleza asincrónica del funcionamiento de los autómatas con respecto al entorno externo. Solo habla de tiempo discreto, en el que el cambio de estado se lleva a cabo durante un período arbitrariamente pequeño, pero no igual a cero, en tiempo real. Y la razón de las transiciones es el estado actual y las señales de entrada de la máquina, donde las consecuencias son la instalación de un nuevo estado y los valores de las señales de salida de la máquina (para más detalles sobre la definición de máquinas, consulte [6]).

La teoría de los autómatas es flexible para determinar el tiempo discreto, que es un modelo en tiempo real. Por lo tanto, un ciclo de tiempo discreto puede tener un valor fijo o flotante de un intervalo en tiempo real, y de acuerdo con esto, las máquinas se llaman síncronas o asíncronas. Al mismo tiempo, el intervalo de tiempo asociado con el reloj puede tener cualquier valor, incluido un valor infinitamente pequeño, pero no igual a cero.

Observación 2. Un modelo de máquina de estados finitos es uno de los pocos modelos formales que incluye en su definición un modelo en tiempo real de forma explícita.

Como resultado, la velocidad formalmente "infinita" del autómata activo permite que cualquier evento sea tratado como una señal de entrada potencial (en términos de UML, la condición [11] le corresponde). La máquina solo necesitará "capturar" tales eventos / señales y pausas entre ellos. Todo esto define realmente el protocolo para el trabajo conjunto del medio y la máquina. El protocolo también debería resolver el problema de reconocer sucesivamente eventos idénticos recibidos. Sin esto, por ejemplo, dos símbolos idénticos, recibidos uno tras otro, pueden ser percibidos como uno.

Formalmente, los matices del procesamiento de eventos no son significativos (ver el mismo autómata abstracto), pero en la implementación práctica de algoritmos construidos por el tipo de modelo de evento, deben tenerse en cuenta. En el caso de la biblioteca Qt, su contabilidad está oculta en las clases de implementación del autómata. A continuación, tendremos en cuenta las diferencias entre eventos y autómatas clásicos utilizando el ejemplo de la implementación de la calculadora más simple de [1], donde se proporciona su "implementación de eventos". En contraste con esta solución, se crearán modelos equivalentes basados ​​en la clásica máquina de estados finitos.

3. Modelos de calculadora

Entonces, comencemos ... ¿Llamamos señales de eventos, eventos de autómatas ordinarios ... o en el orden inverso y / o viceversa? Ugh! Confundido En resumen, la completa "globulosa cuzdra shteko budlanula" y algo "rizos". Para saber quién es quién, qué y qué llamar, la forma más segura es elegir un "bokra" específico y "golpearlo" ... El programa de "calculadora automática" seguirá siendo un "lado".

3.1. Modelo de calculadora activa

En la fig. 1 muestra el modelo original de la clase Calculadora de [1]. En apariencia, parece una máquina abstracta clásica sin salida. La diferencia es que Qt conecta acciones cuando entra y sale de un estado. En la salida, se activan por la señal de salida (), y al ingresar al estado, por la señal de entrada (). Pero, notamos, estas acciones no están representadas en el gráfico de ninguna manera.

Si comparamos el modelo en la Fig. 1 con un autómata con un estado abstracto (sus otros nombres son autómata estructural y lógico), se puede ver fácilmente que las acciones a la salida del estado corresponden a las señales del autómata Mealy, y las acciones a la entrada corresponden a las señales del autómata Moore.
Observación 3. Además, considerando la implementación del software del modelo, no hablaremos de señales, eventos, condiciones, etc., sino de las acciones de los autómatas, suponiendo que a nivel de programa estén asociadas con ciertas acciones del programa, que en el caso general representado por funciones de software.

El llamado autómata combinado de Mili-Moore (o un autómata mixto diferente [12]), equivalente al autómata de la Fig. 1, se muestra en la Fig. 2, donde las funciones correspondientes a las señales de entrada y salida del autómata también se muestran a la derecha del gráfico.


Fig.1. Diagrama de máquina de eventos de calculadora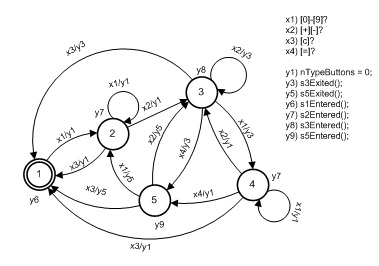


Fig.2. Calculadora de la clase de autómatas del conde Miley-Moore

Para un modelo similar a un autómata en la Fig. 2, por acciones de entrada / salida nos referimos a predicados y acciones que son funciones de programa-métodos de clases [autómatas]. Los predicados analizan el estado actual de los elementos de memoria (variables, propiedades de clase) de ninguna manera (¡esto es importante!) Sin afectarlos, pero dependiendo de su valor, devuelve un valor booleano. Las acciones de un valor no regresan, sino que cambian los elementos de memoria.
De la fig. 2 se deduce que el modelo de la calculadora, como el "cuadro negro", tiene cuatro canales de entrada y siete canales de salida en términos del número de predicados y acciones. Es fácil ver que, en comparación con un autómata abstracto, que por definición no tiene más de un canal de entrada y uno de salida, un autómata estructural que tiene muchos canales es más universal, flexible y conveniente.

El modelo de la fig. 2 puede simplificarse "pegando" los estados 1 y 2. Para hacer esto, primero debe convertir el autómata original en un autómata Mealy. Lo obtenemos cargando los arcos que ingresan al estado de las señales con las señales representadas por las señales de los vértices del autómata Moore. Después de esto, la operación de pegado se hace evidente. El resultado de pegar estados al estado 2, que ahora se convierte en inicial, se muestra en la Fig. 3)


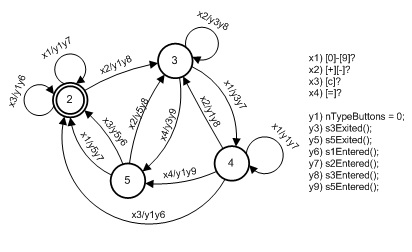Fig.3. El resultado de la transformación y pegado de los estados del autómata en la Fig. 2

Explique la acción y1 y la variable nTypeButtons. En total, implementan un protocolo que simula eventos. La variable nTypeButtons determina el tipo de símbolos de entrada del autómata dividiéndolos en símbolos digitales, símbolos de operación, el símbolo de "reinicio" y el símbolo de "igual". Su valor igual a cero significa la ausencia de caracteres de entrada (no se presiona ninguna de las teclas de la calculadora). Después de procesar el símbolo, esto también significa que el símbolo de entrada se percibe automáticamente. Esto bloquea la respuesta al carácter de entrada.

El código para la clase de la calculadora creada en el marco del entorno de programación automática de componentes visuales (VKPa) [5] se muestra en los listados 1, 2.


Vamos a explicar En VKPa, cualquier clase de autómata hereda las propiedades de la clase de autómata base LFsaAppl. El método Create () crea copias de las clases incluidas en las bibliotecas dinámicas de procesos automáticos. El método virtual MooreAction () se superpone cuando se selecciona un modelo de autómata Moore, que define acciones asociadas con los estados del autómata. Los métodos x [n] e y [n] son ​​los predicados y las acciones asociadas con los canales de entrada / salida del autómata. El algoritmo de comportamiento de la clase [autómata] está representado por la tabla de transición (ver Listado 2), que consiste en una matriz de cadenas de tipo LArc. El resto del código repite el código de la clase de origen Calculadora.


El Listado de avisos 2 contiene tres tablas de salto (dos están comentadas). Así es como se realizan las capacidades de control dedicado cuando, después de eliminar el comentario, el comportamiento de la clase se puede cambiar "por clic" sin afectar sus métodos y propiedades. El método y10 y la línea correspondiente en la tabla de transición (vea la línea marcada con el comentario SWICH) se introdujeron para simular la tecnología SWITCH (para más detalles ver [9]) dentro del marco de la tecnología VKPA. En este caso, el comportamiento de cualquier autómata se modela mediante una llamada cíclica al operador SWITCH, que imita el comportamiento del autómata (aquí el autómata VKPa actúa como un entorno externo).

3.2. Modelo de calculadora pasiva

El modelo de calculadora activa escanea constantemente los canales de entrada. Tan pronto como el valor de la variable nTypeButtons se vuelve distinto de cero, esto sirve como un signo de la llegada del siguiente símbolo a la entrada del autómata. Como resultado, la transición y la acción y1 se activan, restableciendo la variable nTypeButtons, bloqueando la reactivación automática de la máquina por el mismo carácter.
A diferencia del modelo de "calculadora activa", un autómata de eventos no puede, por definición, reprocesar un símbolo de entrada. Ahora está claro que "las mayores dificultades en el uso del enfoque de autómatas ... en sistemas de eventos" parecen reducirse a suprimir la actividad de un autómata activo y vincular su funcionamiento a eventos. Mostramos el procedimiento para cambiar a un autómata pasivo utilizando el ejemplo de la "calculadora activa" recién creada.
El entorno VKPa contiene un modo de operación paso a paso introducido para depurar procesos automáticos. Pero se puede usar para simular máquinas de eventos. Para hacer esto, 1) configure el espacio del autómata en el que se coloca el autómata un modo de operación paso a paso (tenga en cuenta, no un autómata separado, sino todo el espacio del autómata que contiene autómatas), y 2) relacione los momentos de ocurrencia de eventos con la ejecución de un paso discreto de la operación del espacio. El Listado 3 muestra cómo hacer esto, reflejando solo los cambios realizados en el modelo (el encabezado de clase permanece sin cambios).


Aquí, en primer lugar, se introduce un estado [inicial] adicional, en el que se verifica la referencia al espacio donde se encuentra la máquina y el enlace al objeto que determina las propiedades del espacio (incluido su modo de operación). Eh forma la acción de y12. Cuando se establecen los enlaces, hay una transición al estado inicial [anterior] del modelo de calculadora con la instalación de un modo de operación paso a paso del espacio del autómata.

Además, el modelo opera en un modo paso a paso de operación espacial. El lanzamiento de un paso implementa el código insertado en los controladores de eventos asociados con la entrada del siguiente carácter (consulte el Listado 3 para ver los cambios realizados en los métodos digitButtonPressed y operationButtonPressed).

4. ¿Por qué?

¿Por qué inventar algo si hay, como se puede suponer, un modelo de evento más avanzado de D. Harel? Y cómo pensar de manera diferente si se ejecutó en UML, Stateflow, en la biblioteca Qt, etc. etc. y no hay mucho pánico por sus defectos. Bueno, llamaron a las señales eventos y convirtieron la máquina activa en una pasiva ... Y si el modelo, como dicen, también es formalmente equivalente a las máquinas clásicas de Mili / Moore, ¿cómo no creer en él? Y así es, si todas estas declaraciones se toman solo por fe ...

Tome el comienzo del evento (esto es exactamente lo que hicimos anteriormente). Un autómata estructural clásico tiene, por ejemplo, muchos canales de entrada, cada uno de los cuales está asociado con una señal, y pueden procesarse simultáneamente / en paralelo. Pero UML dice que "cada objeto puede procesar solo un evento a la vez" e incluso "si ocurren dos eventos simultáneamente, el objeto aún los procesará uno a la vez" [10]. Por lo tanto, en el nivel de definición, las señales y los eventos son equivalentes, pero el idilio colapsa en el proceso de implementación de las transiciones del modelo.

Considere el ejemplo con el que comienzo a probar / aprender cualquier idioma o tecnología. Se trata de la implementación de software del modelo de elemento AND-NOT. A nivel estructural, corresponde a la "caja negra", que tiene dos canales de entrada y una salida, y en el algoritmo, el autómata que se muestra en la Fig. 4)


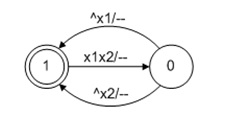Fig. 4. El modelo de autómata del elemento Y NO

Es comprensible cómo crear un modelo de procedimiento normal (ver el Listado 4) o cómo implementar un autómata en el CPSU (ver el Listado 5), pero no es muy claro cómo repetir esto sobre la base del autómata de eventos de la biblioteca Qt debido al problema de implementar la transición desde el estado "1" para indicar "0", que requiere el análisis simultáneo de varios eventos.

Listado 4. Implementación de objetos del modelo de procedimiento AND-NOT



Por lo tanto, deje que la implementación del modelo de evento del elemento NAND en el marco de las clases de autómatas Qt sea "tarea" para los Habrovans. Solo puedo citar su decisión en Stateflow como una "guinda del pastel". Se muestra en la fig. 5. El alivio de Stateflow se usa aquí, lo que permite no marcar la transición con un evento: si no se especifica el nombre del evento, entonces la transición ocurrirá cuando ocurra cualquier evento (consulte la etiqueta de transición en [13] para ver un ejemplo).


Fig. 5. Un modelo de autómata de un elemento AND-NOT en Stateflow

Por lo tanto, las máquinas de estado son un modelo híbrido (activo-pasivo) de una máquina. Es cierto que no está claro cómo se comportará la máquina en ausencia de eventos. Se puede suponer que se "congelará" en anticipación de los eventos. ¿Y si no lo serán? Es decir Al final, es más probable que sea un modelo de máquina pasiva que activa. Aunque solo en apariencia es difícil distinguirlo de este último.

5. Conclusión

En relación con los eventos, podemos decir que, debido a la actividad, la implementación del modelo clásico de autómatas parece preferible al modelo de autómatas síncronos. Si hablamos de programación automática en general, el paquete de extensión Stateflow demuestra lo que puede ser un tipo de programación completamente diferente. Pero, desafortunadamente, hasta ahora solo en perspectiva, porque Los problemas persisten debido al modelo computacional Stateflow, que esencialmente sigue siendo un diagrama de bloques. Parece que precisamente por estas razones, junto con los autómatas, la programación visual en Statefow está representada por la notación de diagramas de flujo.

Descubrir dónde está la programación automática real y dónde está su imitación es uno de nuestros principales objetivos. En el artículo anterior [5], resolvimos una de las tareas básicas planteadas: formulamos el concepto de programas de autómatas. A continuación, debe lidiar con la definición de un modelo de gestión de programas que debe ser autómata finito y efectivo y conveniente para los programadores.

Habiendo lidiado con los eventos, sentamos las bases para tal trabajo. En otros artículos, ya entenderemos los detalles del modelo propuesto por D. Harel. Corriendo un poco más adelante, decimos que, para decirlo sin rodeos, distorsionó la comprensión de los autómatas. Pero, por otro lado, aquí debemos darle la razón, ella reveló problemas que no permitirían, sin ella, formar una programación automática efectiva dentro del marco del modelo clásico que atraería a los programadores.

Descubrimos anteriormente que, al menos, a nivel de evento, los autómatas clásicos no tienen problemas. Lo entenderemos más ... Mientras tanto, esto es solo el comienzo. Estamos esperando muchas cosas interesantes y, tenga en cuenta, no ir más allá de la teoría clásica de los autómatas. Esto es crucial si queremos una programación verdaderamente automatizada. ¡Te deseamos éxito! :)

Referencias

1. Borovsky A.N. Qt4.7. Programación práctica en C ++. - SPb.: BHV-Petersburgo, 2012 .-- 496 p.
2. BUCH G., RAMBO J., JACOBSON I. UML. Manual de usuario. Segunda edicion. Akademiya IT: Moscú, 2007 .-- 493 p.
3. Shalyto A. A. Una nueva conferencia sobre programación automática. 2019, [Recurso electrónico], Modo de acceso: www.youtube.com/watch?v=PPWTxceMutk&feature=youtu.be , gratis. Yaz Ruso (fecha de tratamiento 5 de diciembre de 2019).
4. Flujo de estado. www.mathworks.com/products/stateflow.html , gratis. Yaz Ingles (fecha de circulación 7.01.2020).
5. Máquina de Turing, como modelo de programas de autómatas. habr.com/en/post/481998 , gratis. Yaz Ruso (fecha de circulación 7.01.2020).
6. Melikhov A.N. Gráficos orientados y máquinas de estados finitos. - M .: Nauka, 1971. - 416 p.
7. KUDRYAVTSEV VB, Aleshin S.V., PODKOLZIN A.S. Introducción a la teoría de autómatas - M.: Ciencia. Ch. ed. Phys.-Math. lit., 1985 .-- 320 p.
8. Tukkel N.I., Shalyto A.A. Implementación de autómatas al programar sistemas de eventos. "Programador", 2002. No. 4. C.74-80.
9. Polikarpova N., A. Shalyto A. Programación de autómatas. 2ª ed., San Petersburgo.: Peter, 2011 .-- 176 p.
10. Rambo J., Jacobson A., Butch G. UML: referencia especial. - San Petersburgo: Peter, 2002 .-- 656 p.
11. Goma H. ​​UML. Diseño de sistemas en tiempo real, aplicaciones paralelas y distribuidas: Per. del ingles - M .: DMK Press, 2002. - 2002. - 704 p.
12. SHALYTO A.A. Tecnología SWITCH. Algoritmización y programación de tareas de control lógico. San Petersburgo: Nauka, 1998.628 s.
13. Rogachev G.N. Anotaciones de flujo de estado. bourabai.kz/cm/stateflow13.htm , gratis. Yaz Ruso (fecha de apelación 01.10.2020).