capítulos anteriores

30. Interpretación de la curva de aprendizaje: sesgo grande

Suponga que su curva de error en una muestra de validación se ve así:

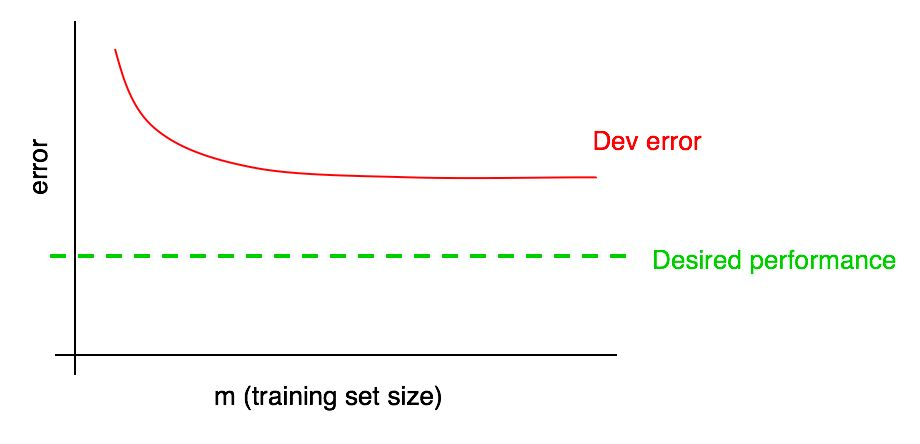
Ya hemos dicho que si un error de algoritmo en la muestra de validación alcanza una meseta, es poco probable que alcance el nivel de calidad deseado simplemente agregando datos.

Pero es difícil imaginar cómo se verá la extrapolación de la curva de la dependencia de la calidad del algoritmo en la muestra de validación (error de desarrollo) al agregar datos. Y si la muestra de validación es pequeña, entonces responder esta pregunta es aún más difícil debido al hecho de que la curva puede ser ruidosa (tener una gran extensión de puntos).

Supongamos que agregamos a nuestro gráfico una curva de la dependencia de la magnitud del error en la cantidad de datos de la muestra de prueba y obtuvimos la siguiente imagen:

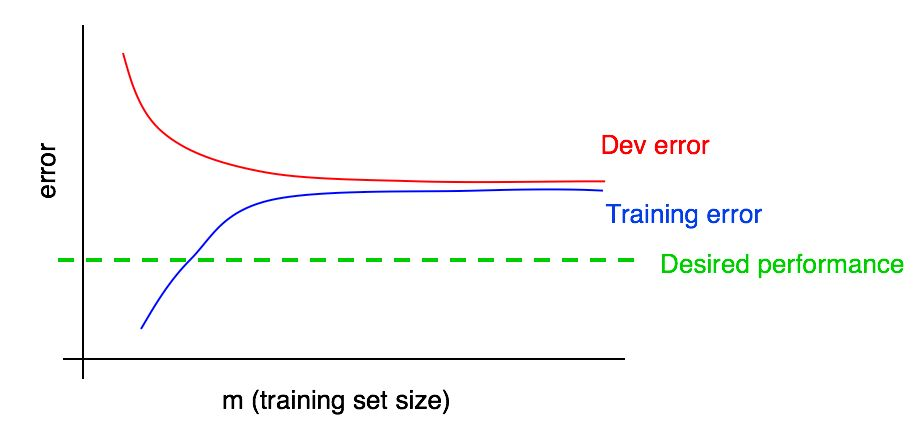
Al observar estas dos curvas, puede estar absolutamente seguro de que agregar datos nuevos por sí solo no dará el efecto deseado (no permitirá aumentar la calidad del algoritmo). ¿Dónde se puede llegar a esta conclusión?
Recordemos los siguientes dos puntos:

• Si agregamos más datos al conjunto de entrenamiento, el error del algoritmo en el conjunto de entrenamiento solo puede aumentar. Por lo tanto, la línea azul de nuestro gráfico no cambiará o se arrastrará y se alejará del nivel de calidad deseado de nuestro algoritmo (línea verde).
• La línea de error roja en la muestra de validación suele ser más alta que la línea de error azul del algoritmo en la muestra de entrenamiento. Por lo tanto, bajo cualquier circunstancia concebible, agregar datos no conducirá a una disminución adicional en la línea roja, no lo acercará al nivel de error deseado. Esto es casi imposible, dado que incluso el error en la muestra de entrenamiento es mayor de lo deseado.

La consideración de ambas curvas de la dependencia del error del algoritmo en la cantidad de datos en las muestras de validación y entrenamiento en el mismo gráfico le permite extrapolar con mayor confianza la curva de error del algoritmo de aprendizaje a partir de la cantidad de datos en la muestra de validación.

Supongamos que tenemos una estimación de la calidad deseada del algoritmo en forma de un nivel óptimo de errores en nuestro sistema. En este caso, los gráficos anteriores son una ilustración de un caso estándar de "libro de texto" de cómo se ve la curva de aprendizaje con un alto nivel de sesgo removible. En el tamaño de muestra de entrenamiento más grande, presumiblemente correspondiente a todos los datos a nuestra disposición, existe una gran brecha entre el error del algoritmo en la muestra de entrenamiento y la calidad deseada del algoritmo, lo que indica un alto nivel de sesgo evitado. Además, la brecha entre el error en la muestra de entrenamiento y el error en la muestra de validación es pequeña, lo que indica una pequeña extensión.

Anteriormente, discutimos los errores de los algoritmos entrenados en muestras de entrenamiento y validación solo en el punto más a la derecha sobre el gráfico, que corresponde al uso de todos los datos de entrenamiento que tenemos. La curva de las dependencias del error en la cantidad de datos de la muestra de entrenamiento, construida para diferentes tamaños de la muestra utilizada para el entrenamiento, nos da una imagen más completa de la calidad del algoritmo entrenado en diferentes tamaños de la muestra de entrenamiento.

31. Interpretación de la curva de aprendizaje: otros casos

Considere la curva de aprendizaje:

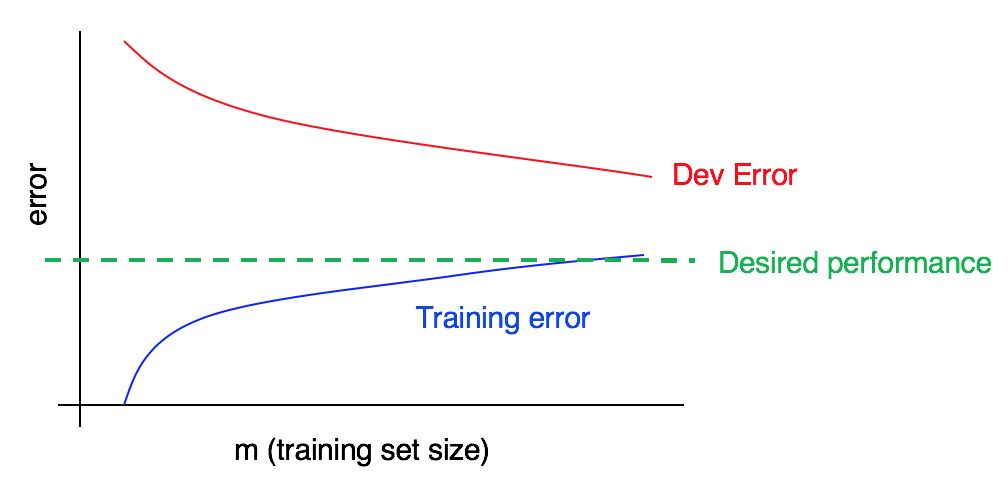
¿Hay un alto sesgo, un alto análisis, o ambos a la vez?

La curva de error azul en los datos de entrenamiento es relativamente baja, la curva de error roja en los datos de validación es significativamente más alta que el error azul en los datos de entrenamiento. Por lo tanto, en este caso, el sesgo es pequeño, pero la propagación es grande. Agregar más datos de entrenamiento puede ayudar a cerrar la brecha entre el error en la muestra de validación y el error en la muestra de entrenamiento.

Ahora considere este cuadro:

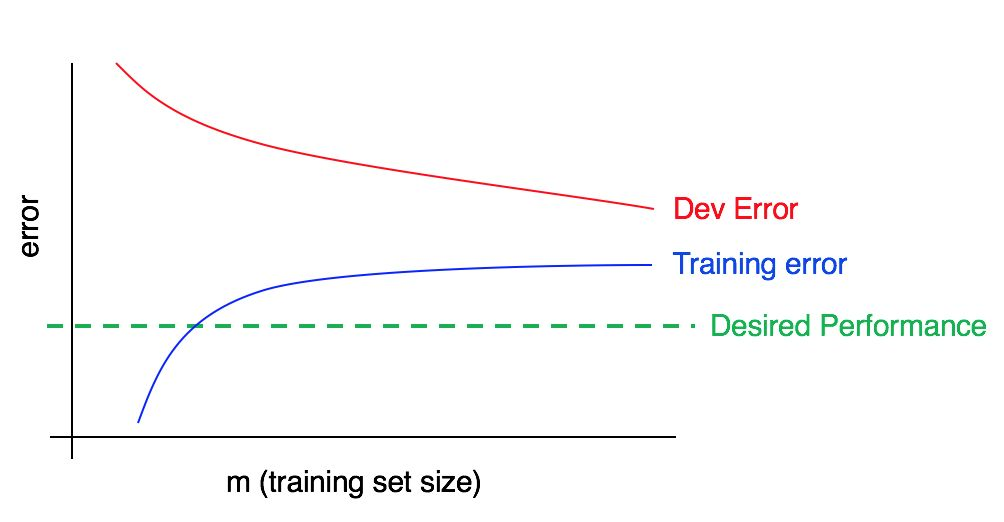
En este caso, el error en la muestra de entrenamiento es grande; es significativamente más alto que el algoritmo correspondiente al nivel de calidad deseado. El error en la muestra de validación también es significativamente mayor que el error en la muestra de entrenamiento. Por lo tanto, estamos lidiando simultáneamente con un gran sesgo y dispersión. Debe buscar formas de reducir, compensar y dispersar su algoritmo.

32. Construyendo curvas de aprendizaje

Supongamos que tiene una muestra de entrenamiento muy pequeña, que consta de solo 100 ejemplos. Usted entrena su algoritmo usando un subconjunto de 10 ejemplos seleccionado al azar, luego de 20 ejemplos, luego de 30 y así sucesivamente a 100, aumentando el número de ejemplos con un intervalo de diez ejemplos. Luego, utilizando estos 10 puntos, construye su curva de aprendizaje. Puede encontrar que la curva parece ruidosa (valores más altos o más bajos de lo esperado) para muestras de entrenamiento más pequeñas.

Cuando entrena el algoritmo con solo 10 ejemplos seleccionados al azar, es posible que no tenga suerte y esto resultará ser una submuestra de entrenamiento particularmente "mala" con una mayor proporción de ejemplos ambiguos / incorrectamente marcados. O, por el contrario, puede encontrar una submuestra de entrenamiento particularmente "buena". La presencia de una pequeña muestra de entrenamiento implica que el valor de los errores en las muestras de validación y entrenamiento puede estar sujeto a fluctuaciones aleatorias.

Si los datos utilizados para su aplicación que utilizan el aprendizaje automático están fuertemente sesgados hacia una clase (como con el problema de clasificación de gatos, en el que la proporción de ejemplos negativos es mucho mayor que la proporción de positivos), o si estamos tratando con una gran cantidad de clases (como reconocimiento de 100 especies diferentes de animales), entonces también aumenta la posibilidad de obtener una muestra de entrenamiento particularmente "no representativa" o pobre. Por ejemplo, si el 80% de sus ejemplos son ejemplos negativos (y = 0), y solo el 20% son ejemplos positivos (y = 1), entonces hay una buena posibilidad de que un subconjunto de entrenamiento de 10 ejemplos contenga solo ejemplos negativos, en este caso muy Es difícil obtener algo razonable del algoritmo entrenado.

Si, debido al ruido de la curva de aprendizaje en la muestra de capacitación, es difícil hacer una evaluación de las tendencias, se pueden proponer las siguientes dos soluciones:

• En lugar de entrenar solo un modelo para 10 ejemplos de entrenamiento, seleccionando con reemplazo varias (digamos 3 a 10) diferentes submuestras de entrenamiento al azar de la muestra inicial que consiste en 100 ejemplos. Entrene el modelo en cada uno de ellos y calcule para cada uno de estos modelos el error en la muestra de validación y entrenamiento. Cuente y trace el error promedio en las muestras de capacitación y validación.

  
  

  Comentario del autor: una muestra con un reemplazo significa lo siguiente: seleccione aleatoriamente los primeros 10 ejemplos diferentes de 100 para formar la primera submuestra de capacitación. Luego, para formar la segunda submuestra de entrenamiento, nuevamente tomamos 10 ejemplos, pero sin tener en cuenta los seleccionados en la primera submuestra (nuevamente de los cien ejemplos completos). Por lo tanto, un ejemplo específico puede aparecer en ambas submuestras. Esto distingue una muestra con un reemplazo de una muestra sin reemplazo; en el caso de una muestra sin reemplazo, la segunda submuestra de entrenamiento se seleccionaría de solo 90 ejemplos que no caen en la primera submuestra. En la práctica, el método de selección de ejemplos con o sin sustitución no debería ser de gran importancia, pero la selección de ejemplos con sustitución es una práctica común.

  
  

• Si su muestra de entrenamiento está sesgada hacia una de las clases, o si incluye muchas clases, elija una submuestra "equilibrada" que consta de 10 ejemplos de entrenamiento, seleccionados al azar de 100 muestras de muestra. Por ejemplo, puede estar seguro de que 2/10 ejemplos son positivos y 8/10 negativos. Para resumir, puede estar seguro de que la proporción de ejemplos de cada clase en el conjunto de datos observados es lo más cercana posible a su participación en la muestra de entrenamiento inicial.

  
  

  No me molestaría con ninguno de estos métodos hasta que la representación gráfica de las curvas de error lleve a la conclusión de que estas curvas son excesivamente ruidosas, lo que no nos permite ver tendencias comprensibles. Si tiene una muestra de entrenamiento grande, digamos unos 10,000 ejemplos y la distribución de sus clases no es muy sesgada, es posible que no necesite estos métodos.

  
  

Finalmente, construir una curva de aprendizaje puede ser costoso desde un punto de vista computacional: por ejemplo, necesita entrenar diez modelos, en los primeros 1000 ejemplos, en el segundo 2000, y así sucesivamente hasta que el último contenga 10,000 ejemplos. El entrenamiento modelo en pequeñas cantidades de datos es mucho más rápido que el entrenamiento modelo en muestras grandes. Por lo tanto, en lugar de distribuir uniformemente los tamaños de las submuestras de entrenamiento a lo largo de una escala lineal, como se describió anteriormente (1000, 2000, 3000, ..., 10000), puede entrenar modelos con un aumento no lineal en el número de ejemplos, por ejemplo, 1000, 2000, 4000, 6000 y 10,000 ejemplos. De todos modos, debería darle una comprensión clara de la tendencia de la dependencia de la calidad del modelo en la cantidad de ejemplos de capacitación en las curvas de aprendizaje. Por supuesto, esta técnica es relevante solo si el costo computacional de la capacitación de modelos adicionales es alto.

continuación