Como todos saben, la ordenación puede basarse en intercambios, inserciones, selección, fusión y distribución.
Pero si se combinan diferentes métodos en el algoritmo, entonces pertenece a la clase de clases híbridas.

Este artículo fue escrito con el apoyo de EDISON.
Nos dedicamos a la finalización y el mantenimiento de sitios en 1C-Bitrix , así como al desarrollo de aplicaciones móviles Android e iOS .
¡Nos encanta la teoría de los algoritmos! ;-)
Recordemos rápidamente qué algoritmos de clasificación de clases tienen y cuáles son las características de cada uno de ellos.
Clases de intercambio
Los elementos de la matriz se comparan en pares entre sí y se realizan intercambios por pares desordenados.
El representante más efectivo de esta clase es el legendario
tipo rápido .
Clases de inserción
Los elementos de la parte no ordenada de la matriz se insertan en sus lugares en el área ordenada.
De esta clase, la
clasificación por inserciones simples se usa con mayor frecuencia. Aunque este algoritmo tiene una complejidad promedio de O (
n 2 ), esta clasificación funciona muy rápidamente con arreglos casi ordenados; en ellos la complejidad llega a O (
n ). Además, esta clasificación es una de las mejores opciones para procesar matrices pequeñas.
Ordenar usando el árbol de búsqueda binario también pertenece a esta clase.
Ordenar por selección

En el área desordenada, se selecciona el elemento mínimo / máximo, que se transfiere al final / principio de la parte no ordenada de la matriz.
La clasificación con una elección simple funciona muy lentamente (en promedio O (
n 2 )), pero en esta clase hay una
clasificación difícil
por un montón (también conocido como
clasificación piramidal ), que tiene una complejidad temporal de O (
n log
n ), y, lo cual es muy valioso, No hay casos degenerados de esta clasificación, independientemente de los datos entrantes. Por cierto, esta clasificación tampoco tiene los mejores casos para los datos entrantes.
Combinar clasificaciones
Las áreas ordenadas se toman en la matriz y se fusionan, es decir, las subcadenas ordenadas más pequeñas se combinan en una subcadena ordenada más grande.
Si se ordenan dos submatrices, combinarlas es una operación fácil de implementar y rápida. La otra cara de la moneda es que la fusión casi siempre requiere el costo de memoria adicional de O (
n ), aunque se conoce un número extremadamente pequeño de opciones de clasificación de fusión particularmente sofisticadas, donde el costo de la memoria es O (1).
Ordenar por distribución
Los elementos de la matriz se distribuyen y redistribuyen en clases hasta que la matriz acepta un estado ordenado.
Los elementos se dispersan en grupos, ya sea en función de su valor (los llamados
ordenamientos de conteo ) o en función del valor de los dígitos individuales (estos ya son
ordenamientos bit a bit ).
La clasificación de cubos también pertenece a esta clase.
Una característica de la clasificación por distribución es que no utilizan comparaciones por pares de elementos entre ellos, o que tales comparaciones están presentes en pequeña medida. Por lo tanto, la ordenación por distribución suele adelantarse a la velocidad, por ejemplo, la ordenación rápida. Por otro lado, la ordenación por distribución a menudo requiere mucha memoria adicional, ya que los grupos de elementos redistribuidos constantemente deben almacenarse en algún lugar.
Las disputas sobre qué clasificación es
la mejor son muy frecuentes, pero el hecho es que no existe y no puede ser un algoritmo ideal para todas las ocasiones. Por ejemplo, la ordenación rápida es realmente muy rápida (pero no la más rápida) en la mayoría de las situaciones, pero también se encuentra con casos degenerados en los que se produce un bloqueo. La ordenación por inserciones simples es lenta, pero para las matrices casi ordenadas evitará fácilmente otros algoritmos. La ordenación del montón funciona bastante rápido con cualquier dato entrante, pero no tan rápido como otras clasificaciones bajo ciertas condiciones y no hay forma de acelerar la pirámide. La ordenación por fusión es más lenta que la ordenación rápida, sin embargo, si hay subarreglos ordenados en la matriz, entonces es más rápido fusionarlos que por ordenación rápida. Si la matriz tiene muchos elementos repetidos o si ordenamos las filas, lo más probable es que la mejor opción sea ordenar por distribución. Cada método es especialmente bueno en su situación más favorable.
Sin embargo, los programadores continúan inventando las clasificaciones más rápidas del mundo, sintetizando los métodos más efectivos de diferentes clases. Veamos qué tan exitoso es para ellos.
Dado que en el artículo se mencionan muchos algoritmos no triviales, solo cubro brevemente los principios básicos de su trabajo, sin sobrecargar el artículo con animaciones y explicaciones detalladas. En el futuro habrá artículos separados, donde habrá dibujos animados para cada algoritmo y matices sutiles detallados.
Insertar + Fusionar
Una conclusión puramente empírica es que la fusión y / o inserción se usan con mayor frecuencia en híbridos. En la mayoría de las clasificaciones, se encuentra uno u otro método, o ambos juntos. Y hay una explicación lógica para esto.
Los inventores de clasificación a menudo se esfuerzan por crear algoritmos paralelos que ordenan simultáneamente diferentes partes de una matriz. La mejor manera de lidiar con varias submatrices ordenadas es fusionarlas; esta será la más rápida.
Los algoritmos modernos a menudo usan recursividad. Durante un descenso recursivo, la matriz generalmente se divide en dos partes; en el nivel más bajo, se ordena la matriz. Al regresar a niveles más altos de recursión, surge la cuestión de combinar submatrices ordenadas en niveles más bajos.
En cuanto a los insertos, en los algoritmos híbridos en ciertas etapas a menudo se obtienen subarreglos aproximadamente ordenados, que se llevan mejor al pedido final con la ayuda de insertos.
Este grupo contiene tipos híbridos, en los que hay una fusión e inserción, y estos métodos se usan de manera muy diferente.
Ordenar por inserción de fusión
Algoritmo de Ford Johnson :: Algoritmo de Ford-Johnson
Fusionar + Insertar

Una forma muy antigua, ya en 1959. Se describe en detalle en el trabajo inmortal de Donald Knuth, "El arte de la programación", Volumen 3, "Clasificación y búsqueda", Capítulo 5, "Clasificación", Sección 5.3, "Clasificación óptima", subsección, "Clasificación con un número mínimo de comparaciones" y parte "Clasificación por inserciones y fusión". .
La clasificación ahora no tiene ningún valor práctico, pero es interesante para aquellos que aman la teoría de los algoritmos. Se considera el problema de encontrar una manera de ordenar
n elementos con el menor número de comparaciones. Se propone una modificación heurística no trivial para la clasificación de inserción (una inserción de este tipo que no encontrará en ningún otro lugar) utilizando
números de Jacobstal para minimizar el número de comparaciones. Hasta la fecha, también se sabe que esta no es la mejor opción y que puede esquivar aún más hábilmente y obtener incluso menos comparaciones. En general, la clasificación académica estándar no es de uso práctico, pero para los conocedores del género es un placer desmontar tales trucos con un sesgo algebraico.
Tim Sort :: Timsort
Insertar + Fusionar
 Publicado por Tim Peters hace 15 años y ahora
Publicado por Tim Peters hace 15 años y ahoraEsta clasificación en Habré se recuerda muy a menudo.
Tesis: en una matriz, se buscan subarreglos pequeños casi ordenados para los que se utiliza la clasificación de inserción. Estas submatrices se fusionan usando merge.
La fusión en TimSort es la parte más interesante: la fusión ascendente clásica se optimiza aún más para diferentes situaciones. Por ejemplo, se sabe que la fusión es más eficiente si las submatrices unidas tienen aproximadamente el mismo tamaño. En TimSort, si los tamaños son muy diferentes, luego de acciones adicionales hay un ajuste (podemos decir que parte de los elementos "fluirán" del subconjunto más grande a uno más pequeño, después de lo cual la fusión continuará en el modo estándar). También se proporcionan varias situaciones insidiosas, por ejemplo, si en un subconjunto todos los elementos serán menores que en otro. En este caso, la comparación de elementos de ambas submatrices estará inactiva. El procedimiento de fusión modificado "notará" un desarrollo indeseable de eventos en el tiempo, y si está "convencido" de una opción pesimista mediante la búsqueda binaria, cambiará a una opción de procesamiento más óptima.
En promedio, esta clasificación funciona un poco más lento que QuickSort, sin embargo, si la matriz entrante contiene un número suficiente de subsecuencias ordenadas de elementos, entonces la velocidad aumenta significativamente y aquí TimSort se adelanta al resto.
Clasificación de fusión de bloques :: Clasificación de fusión de bloques
Wiki-sort :: Wiki-sort
Holy Grail Sort :: Grailsort
Insertos + Fusionar + Cubos
 Animación de clasificación de fusión de bloques de Wikipedia.
Animación de clasificación de fusión de bloques de Wikipedia.Este es un algoritmo muy nuevo (2008) y al mismo tiempo muy prometedor. El hecho es que el problema relativamente importante de la fusión es el costo de la memoria adicional. Por lo general, donde existe la fusión, también hay complejidad de memoria O (
n ).
Pero WikiSort está diseñado para que la fusión ocurra sin el uso de memoria adicional, entre los tipos de fusión, en este sentido, esta es una instancia muy rara. Además, el algoritmo es estable. Bueno, si la clasificación de fusión convencional tiene la mejor velocidad algorítmica O (
n log
n ), entonces en la clasificación wiki este indicador es O (
n ). Hasta hace poco, se creía que fusionar la clasificación con ese conjunto de características era imposible en principio, pero los programadores chinos sorprendieron a todos.
El algoritmo es muy complicado de explicar en un par de oraciones. Pero algún día escribiré un habrast separado sobre él.
Inicialmente, el algoritmo se llamaba sin nombre Block Merge Sort, sin embargo, con la mano ligera de Tim Peters, que estudió la clasificación en detalle (para determinar si algunas de sus ideas deberían transferirse a TimSort), el nombre WikiSort se adhirió a él.
El habruiser prematuro que partió
Mrrl trabajó independientemente durante varios años en la clasificación de fusión, que sería simultáneamente rápido con cualquier dato entrante, económico en memoria y estable.
Sus búsquedas creativas fueron exitosas y más tarde llamó al algoritmo desarrollado una clasificación del Santo Grial (ya que satisface todos los altos requisitos de "clasificación perfecta"). La mayoría de las ideas de este algoritmo son similares a las implementadas en WikiSort, aunque estos tipos no son idénticos y se desarrollan independientemente uno del otro.
Clasificación de tabla hash :: Clasificación de tabla hash
Distribución + Insertar + Fusionar
La matriz se divide recursivamente por la mitad, hasta que el número de elementos en las submatrices resultantes alcanza un cierto valor umbral. En el nivel más bajo de recursión, se produce una distribución aproximada (usando una tabla hash) y la submatriz se ordena por inserciones. Luego hay un retorno recursivo a niveles más altos, las mitades ordenadas se combinan mediante la fusión.
Hablé un poco más sobre este algoritmo hace un
mes .
Ordenación rápida como primaria
Después de fusionarse e insertarse, el tercer lugar en el desfile de éxito híbrido está firmemente en manos de la clasificación rápida favorita de todos.
Este es un algoritmo muy eficiente, pero también hay casos degenerados. Algunos inventores están tratando de hacer que QuickSort sea completamente invulnerable a cualquier dato entrante incorrecto y sugieren complementarlo con ideas fuertes de otros tipos.
Clasificación introspectiva :: Introsort, Clasificación introspectiva, std :: sort
Rápido + montón + insertos
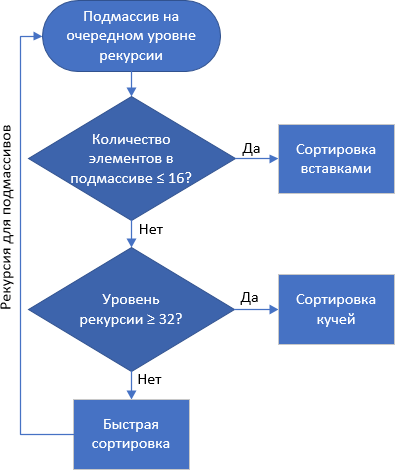
La ordenación en montón funciona de manera algo más lenta que la ordenación rápida, pero al mismo tiempo, a diferencia de QuickSort, no tiene casos degenerados: la complejidad del tiempo algorítmico promedio, mejor y peor es O (
n log
n ).
Por lo tanto, David Musser propuso estar a salvo durante la clasificación rápida: si hay demasiado anidamiento, esto se considera un ataque al sistema, que deslizó una matriz "mala". Se produce el cambio a la clasificación por un montón, que no es megabyte, pero tampoco es lento para hacer frente
a los datos entrantes.
C ++ tiene un algoritmo llamado std :: sort, que es una implementación de ordenación introspectiva. Una pequeña adición: si en el siguiente nivel de recursión el
número de elementos de la submatriz es ≤ 16 , entonces la clasificación de inserción se aplica a la submatriz.
Multikey sort :: Multikey sort
Bitwise Quick Sort :: Clasificación rápida de Radix
Rápido + rangos
Ordenación rápida, solo los valores de los elementos de la matriz se comparan entre sí, pero sus dígitos individuales (primero, organizamos los dígitos más altos de esta manera, nos movemos de los más pequeños a ellos).
O más o menos: esta es una ordenación de bits por orden superior, la ordenación dentro del siguiente bit se lleva a cabo de acuerdo con el algoritmo de ordenación rápida.
Scatter Sort :: Spreadsort
Rápido + fusión + cubos + descargas
Gestalt de quicksort, merge sort, bucket sort y bitwise sort.
En pocas palabras, no lo explique. Analizaremos este algoritmo en detalle en uno de los siguientes artículos.
Otros híbridos
Tipo de conteo de árboles
Contando + árbol
El algoritmo
propuesto por el usuario
AlexanderUsatov . Contando el orden, el número de claves contadas se almacena en un árbol equilibrado.
J-sort :: J-sort
Montón + insertos
Ya escribí sobre esta clasificación hace
5 años . Todo es bastante simple: primero en la matriz, necesita construir una pila no creciente una vez, y luego hacer exactamente lo contrario: construir una vez no decreciente. Como resultado de la primera operación, el mínimo estará en el primer lugar de la matriz, y los elementos pequeños en su conjunto se moverán significativamente al principio. En el segundo caso, el máximo estará en el último lugar y los elementos grandes migrarán hacia el final de la matriz. En general, obtenemos una matriz casi ordenada con la que hacemos qué. Así es, ordena los insertos.
Referencias
 Inserción de fusión
Inserción de fusión ,
fusión de bloque ,
Tim ,
introspectivo ,
propagación ,
multiciclo Grial
Grial Grial
Grial ,
Hash Table ,
Count / Tree ,
JArtículos de la serie:
De todas las clasificaciones que se presentan aquí, en la aplicación Excel de AlgoLab solo se implementa actualmente la animación Jsort.