Teoría de la información visual (Parte 1)

Traducción de un interesante texto largo dedicado a la visualización de conceptos desde la teoría de la información. En la primera parte, veremos cómo representar gráficamente las distribuciones de probabilidad, su interacción y las probabilidades condicionales. A continuación, trataremos con códigos de longitud fija y variable, veremos cómo se construye el código óptimo y por qué es así. Como suplemento, la paradoja estadística de Simpson se entiende visualmente.

La teoría de la información nos brinda un lenguaje preciso para describir muchas cosas. ¿Cuánta incertidumbre hay en mí? ¿Cuánto conocimiento de la respuesta a la pregunta A me dice acerca de la respuesta a la pregunta B? ¿Cuán similar es un conjunto de creencias a otro? Tuve versiones informales de estas ideas cuando era un niño pequeño, pero la teoría de la información las cristaliza en ideas precisas y poderosas. Estas ideas tienen una gran variedad de aplicaciones, desde compresión de datos hasta física cuántica, aprendizaje automático y las vastas áreas entre ellas.

Desafortunadamente, la teoría de la información puede parecer intimidante. No creo que haya ninguna razón para esto. De hecho, muchas ideas clave se pueden explicar visualmente.

Visualización de distribución de probabilidad

Antes de profundizar en la teoría de la información, pensemos en cómo puede visualizar distribuciones de probabilidad simples. Los necesitaremos más tarde, además, ¡estas técnicas para visualizar probabilidades son útiles en sí mismas!

Estoy en california A veces llueve, ¡pero sobre todo el sol! Digamos que el 75% del tiempo está soleado. Es fácil representar en la imagen:


La mayoría de los días me pongo una camiseta, pero a veces me pongo un impermeable. Supongamos que uso un impermeable el 38% del tiempo. Esto también es fácil de representar.


¿Qué sucede si quiero visualizar ambos hechos al mismo tiempo? Es simple si no interactúan, es decir son independientes Por ejemplo, si eso: que llevo una camiseta o un impermeable hoy no depende del clima la próxima semana. Podemos representar esto usando un eje para una variable y uno para la otra:



Presta atención a las líneas rectas verticales y horizontales que atraviesan. ¡Así es como se ve la independencia! La probabilidad de que use un impermeable no cambiará debido al hecho de que en una semana lloverá. En otras palabras, la probabilidad de que use un impermeable y que llueva la próxima semana es igual a la probabilidad de que use un impermeable por la probabilidad de que llueva. No interactúan

Cuando las variables interactúan, la probabilidad puede aumentar para algunos pares de variables y disminuir para otras. Hay una alta probabilidad de que use un impermeable y llueva porque las variables están correlacionadas, se hacen más probables. Es más probable que use un impermeable en un día cuando llueve que la probabilidad de que use un impermeable en un día y llueva en otro día aleatorio.

Visualmente, parece que algunos de los cuadrados se hinchan con una probabilidad adicional, mientras que los otros cuadrados se estrechan, porque es poco probable que ocurran un par de eventos simultáneamente:



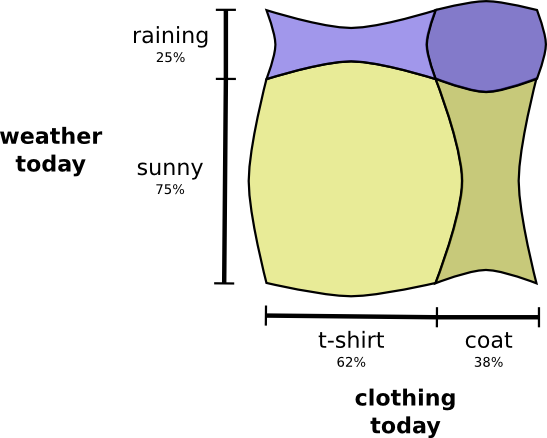
Pero aunque se ve bien, no es muy útil para entender lo que está sucediendo.

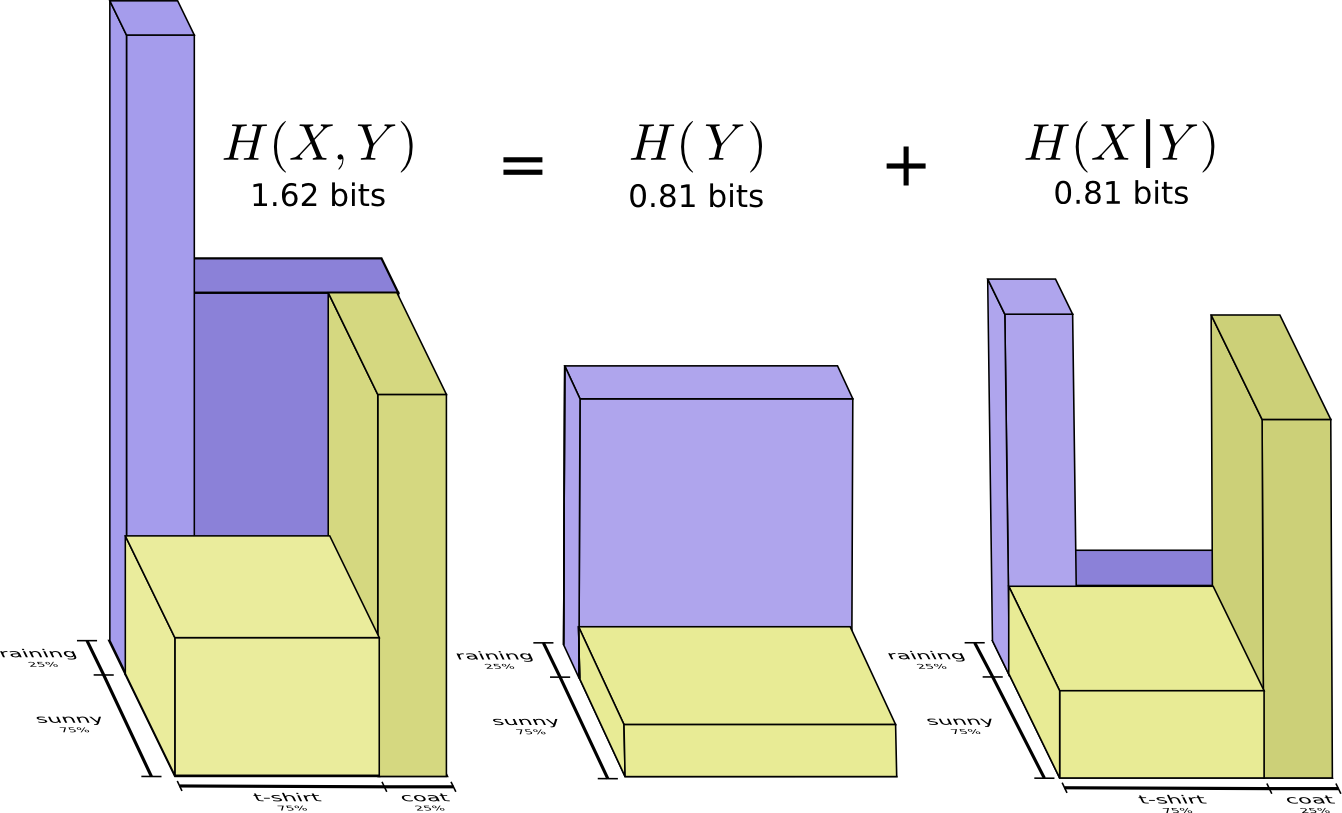
En cambio, centrémonos en una variable como el clima. Conocemos las probabilidades del clima soleado y lluvioso. En ambos casos, podemos considerar las probabilidades condicionales. ¿Cuál es la probabilidad de que use una camiseta si hace sol? ¿Cuál es la probabilidad de que use un impermeable si llueve?


Con una probabilidad del 25%, lloverá. Si llueve, usaré un impermeable con un 75% de probabilidad. Por lo tanto, la probabilidad de que llueva y use un impermeable es del 25% del 75%, que es aproximadamente el 19%. La probabilidad de que esté lloviendo y estoy usando un impermeable es la probabilidad de que esté lloviendo multiplicada por la probabilidad de que use un impermeable si está lloviendo. Lo escribimos así:

$$

$$p (lluvia, abrigo) = p (lluvia) ⋅p (abrigo | lluvia)$$

Este es un ejemplo de una de las identidades más fundamentales de la teoría de la probabilidad:

$$

$$p (x, y) = p (x) ⋅p (y | x)$$

Factorizamos la distribución dividiéndola en un producto de dos partes. Primero, observamos la probabilidad de que una variable, el clima, tome un cierto valor. Luego observamos la probabilidad de que otra variable, mi ropa, tome el valor debido a la primera variable.

Con qué variable comenzar no importa. Podríamos comenzar con mi ropa y luego mirar el clima causado por esto. Esto puede parecer menos intuitivo porque entendemos que existe una relación causal entre el clima que afecta lo que uso y no al revés ... ¡pero funciona de todos modos!

Veamos un ejemplo. Si elegimos un día aleatorio, con una probabilidad del 38%, usaré un impermeable. Si sabemos que estoy en un impermeable, ¿qué posibilidades hay de que llueva? Prefiero usar una gabardina bajo la lluvia que bajo el sol, pero la lluvia en California es rara, y resulta que con un 50% de probabilidad de que llueva. Entonces, la probabilidad de que llueva y use un impermeable es la probabilidad de que lo use (38%), multiplicado por la probabilidad de que llueva si uso un impermeable (50%), que es aproximadamente el 19%.

$$

$$p (lluvia, abrigo) = p (abrigo) ⋅p (lluvia | abrigo)$$

Esto nos da una segunda forma de visualizar la misma distribución de probabilidad.


Tenga en cuenta que los valores de la etiqueta tienen un significado ligeramente diferente al del diagrama anterior: una camiseta y un impermeable son ahora las probabilidades límite, la probabilidad de que use estas prendas sin tener en cuenta el clima. Por otro lado, ahora hay dos marcas de lluvia y sol, porque sus probabilidades dependen del hecho de que usaré una camiseta o impermeable.

(Es posible que haya oído hablar del teorema de Bayes. ¡Puede imaginarlo como una forma de transición entre estas dos formas diferentes de representar la distribución de probabilidad!)

Recuadro: La paradoja de Simpson

¿Son realmente útiles estas técnicas de visualización para distribuciones de probabilidad? Yo creo que si! Un poco más allá, los usamos para visualizar la teoría de la información, pero por ahora los usamos para estudiar la paradoja de Simpson. La paradoja de Simpson es una situación estadística extremadamente poco intuitiva. Es difícil de entender en un nivel intuitivo. Michael Nielsen escribió un excelente ensayo Reinventing Explanation , que explica la paradoja de muchas maneras. Quiero intentar hacerlo yo mismo, utilizando las técnicas que desarrollamos en la sección anterior.

Se están probando dos métodos para tratar los cálculos renales. La mitad de los pacientes reciben tratamiento A, mientras que la otra mitad recibe tratamiento B. Los pacientes que recibieron tratamiento B tenían más probabilidades de recuperarse que los que recibieron tratamiento A.


Sin embargo, los pacientes con cálculos renales pequeños tenían más probabilidades de recuperarse si recibían el tratamiento A. ¡Los pacientes con cálculos renales grandes en el riñón también tenían más probabilidades de recuperarse si recibían el tratamiento A! ¿Cómo puede ser esto?

La esencia del problema es que el estudio no se aleatorizó adecuadamente. Entre los pacientes que recibieron tratamiento A, hubo más pacientes con cálculos renales grandes, y entre los pacientes que recibieron tratamiento B hubo más con cálculos renales pequeños.


Como resultado, los pacientes con cálculos renales pequeños son mucho más propensos a recuperarse en general.

Para comprender mejor esto, podemos combinar los dos diagramas anteriores. El resultado es un gráfico tridimensional con una tasa de recuperación dividida en cálculos renales pequeños y grandes.


Ahora vemos que en el caso de cálculos pequeños y grandes, el tratamiento A es superior al tratamiento B. El tratamiento B se veía mejor solo porque los pacientes a los que se aplicó tenían, en general, ¡más posibilidades de recuperarse!

Códigos

Ahora que tenemos formas de visualizar la probabilidad, podemos sumergirnos en la teoría de la información.

Déjame contarte sobre mi amigo imaginario, Bob. Bob ama mucho a los animales. Él constantemente habla de animales. De hecho, solo habla cuatro palabras: "perro", "gato", "pez" y "pájaro".

Hace un par de semanas, a pesar de que Bob era producto de mi imaginación, se mudó a Australia. Además, decidió que solo quería comunicarse en formato binario. Todos mis mensajes (imaginarios) de Bob se ven así:


Para comunicarnos, Bob y yo necesitamos crear un sistema de codificación, una forma de mostrar palabras en una secuencia de bits.


Para enviar un mensaje, Bob reemplaza cada carácter (palabra) con la palabra de código correspondiente, luego los combina para formar una cadena codificada.

Códigos de longitud variable

Desafortunadamente, los servicios de comunicaciones en Australia imaginaria son caros. Tengo que pagar $ 5 por cada mensaje que recibo de Bob. ¿Mencioné que a Bob le gusta hablar mucho? Para no ir a la quiebra, Bob y yo decidimos averiguar si era posible reducir de algún modo la longitud promedio del mensaje.

Resulta que Bob no pronuncia todas las palabras con la misma frecuencia. Bob ama mucho a los perros. Él habla de perros todo el tiempo. A veces habla de otros animales, especialmente un gato que a su perro le gusta perseguir, pero sobre todo habla de perros. Aquí hay un gráfico de la frecuencia de sus palabras:


Esto es alentador. Nuestro antiguo código usa palabras de código de 2 bits, sin importar con qué frecuencia se usen.

Hay una buena manera de visualizar esto. En el siguiente diagrama, usamos el eje vertical para visualizar la probabilidad de cada palabra $$$p (x)$ y un eje horizontal para visualizar la longitud de la palabra de código correspondiente $$$L (x)$ . Tenga en cuenta que el área resultante es la longitud promedio de la palabra de código que enviamos, en este caso 2 bits.


Podemos ser más inteligentes y hacer que el código sea variable en longitud, donde las palabras de código para palabras comunes se acortan. El problema es que existe una competencia entre las palabras de código: al acortar algunas, nos vemos obligados a alargar otras. Para minimizar la longitud del mensaje, idealmente nos gustaría que todas las palabras de código sean cortas, pero las más cortas deberían usarse ampliamente. Por lo tanto, el código resultante contiene palabras de código más cortas para palabras comunes (por ejemplo, "perro") y palabras de código más largas para palabras raras (por ejemplo, "pájaro").


Vamos a visualizar esto de nuevo. Tenga en cuenta que las palabras de código más comunes son más cortas y las más raras son más largas. Como resultado, tenemos un área más pequeña. Esto corresponde a una longitud de palabra de código esperada más corta. ¡La longitud promedio de la palabra de código es ahora de 1.75 bits!



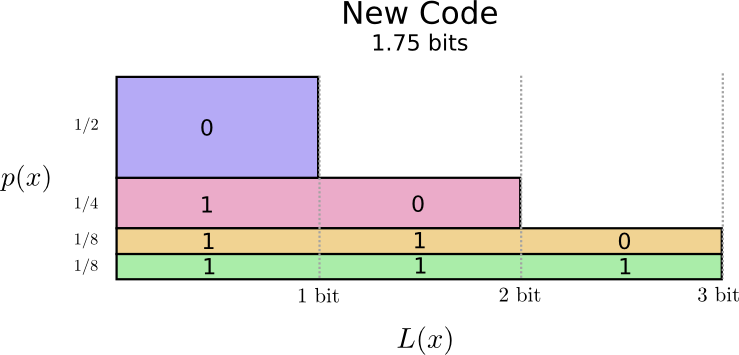
(Quizás se pregunte: ¿por qué no usar 1 por separado como palabra de código? Desafortunadamente, esto causará ambigüedad al decodificar cadenas codificadas. Hablaremos más sobre esto un poco más adelante).

Resulta que este código es el mejor posible. No hay código para esta distribución que nos dé una longitud promedio de palabra de código de menos de 1.75 bits.

Hay un límite fundamental. La transmisión de qué palabra se dijo, qué evento de esta distribución ocurrió, requiere que transmitamos un promedio de al menos 1.75 bits. No importa cuán inteligente sea nuestro código, es imposible lograr que la longitud promedio del mensaje sea menor. Llamamos a este límite fundamental la entropía de distribución ; lo discutiremos con más detalle a continuación.



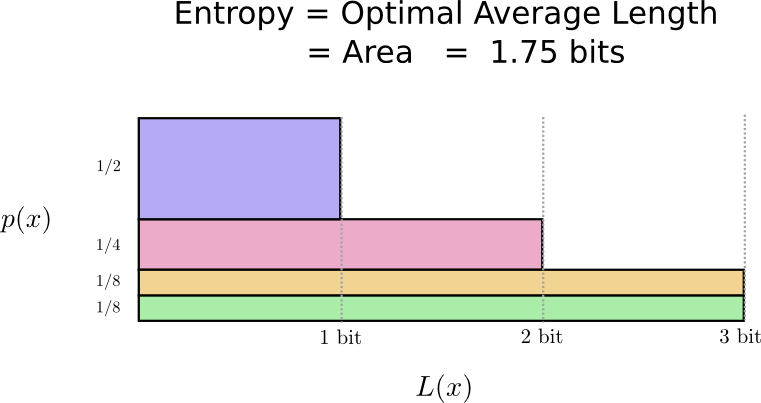
Si queremos entender este límite, debemos entender la compensación entre mantener algunas palabras de código cortas y otras largas. Una vez que resolvamos esto, podemos descubrir cómo son los mejores sistemas de codificación posibles.

Espacio de palabras de código

Hay dos palabras de código con una longitud de 1 bit: 0 y 1. Hay cuatro palabras de código con una longitud de 2 bits: 00, 01, 10 y 11. Cada bit que agregue duplica la cantidad de palabras de código posibles.


Estamos interesados ​​en códigos de longitud variable, donde algunas palabras de código son más largas que otras. Podemos tener situaciones simples cuando tenemos ocho palabras de código de 3 bits de largo. Puede haber mezclas más complejas, por ejemplo, dos palabras de código de longitud 2 y cuatro palabras de código de longitud 3. ¿Qué decide cuántas palabras de código de diferentes longitudes podemos tener?

Recuerde que Bob convierte sus mensajes en cadenas encriptadas, reemplazando cada palabra con su código y concatenándolas.


Hay una pregunta sutil a tener cuidado al crear códigos de longitud variable. ¿Cómo dividimos la cadena codificada en palabras de código? Cuando todas las palabras de código tienen la misma longitud, es fácil: simplemente divida la cadena en partes de esa longitud. Pero como hay palabras de código de varias longitudes, debemos prestar atención al contenido.

Queremos que nuestro código sea exclusivamente decodificable. Y no queremos que sea ambiguo para determinar qué palabras de código forman la cadena codificada. Si tuviéramos un símbolo especial "fin de la palabra clave", sería simple. Pero no tenemos eso: enviamos solo 0 y 1. Necesitamos poder ver la secuencia de palabras de código y determinar dónde termina cada una de ellas.

Es muy sencillo crear códigos que no se puedan descifrar sin ambigüedades. Por ejemplo, imagine que 0 y 01 son ambas palabras de código. Entonces no está claro cuál es la primera palabra de código de la línea 0100111: ¡puede ser esto o aquello! La propiedad que necesitamos es que si vemos una palabra de código específica, no debería incluirse en otra palabra de código más larga. En otras palabras, ninguna palabra de código debe ser un prefijo de otra palabra de código. Esto se llama propiedad de prefijo, y los códigos que la obedecen se llaman códigos de prefijo .

Una forma útil de representar esto es que cada palabra de código requiere sacrificios del espacio de posibles palabras de código. Si tomamos la palabra de código 01, perdemos la capacidad de usar cualquier palabra de código cuyo prefijo sea. Ya no podemos usar 010 o 011010110 debido a la ambigüedad: nos hemos perdido.


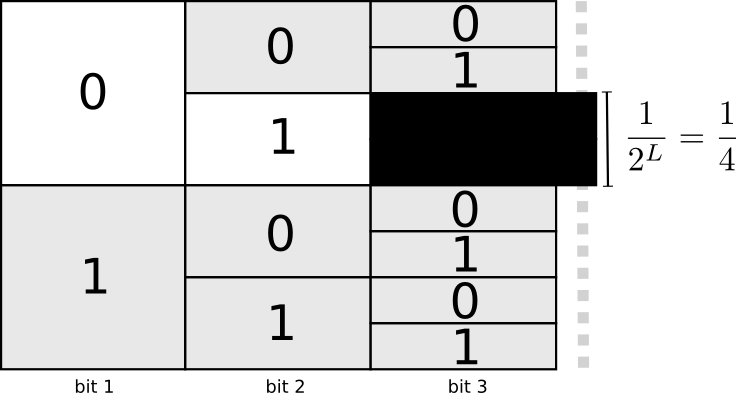
Como una cuarta parte de todas las palabras de código comienza en 01, donamos una cuarta parte de todas las palabras de código posibles. ¡Aquí está el precio que pagamos a cambio del hecho de que tenemos una palabra de código con una longitud de solo 2 bits! A su vez, este sacrificio significa que todas las demás palabras de código deberían ser un poco más largas. Siempre hay una especie de compromiso entre las longitudes de las diferentes palabras de código. Una palabra de código corta requiere que sacrifiques la mayor parte del espacio de palabras de código posibles, lo que evita la brevedad de otras palabras de código. ¡Lo que necesitamos descubrir es cómo comprometernos correctamente!

Codificación óptima

Puede considerarlo como un presupuesto limitado que puede gastar para obtener palabras de código cortas. Pagamos por una palabra de código, sacrificando parte de las posibles palabras de código.

El costo de comprar una palabra de código de longitud 0 es 1, todas las palabras de código posibles, si desea tener una palabra de código de longitud 0, no puede tener ninguna otra palabra de código. El costo de una palabra de código con una longitud de 1, por ejemplo, "0", es 1/2, porque la mitad de las posibles palabras de código comienzan con "0". El costo de una palabra de código de longitud 2, por ejemplo "01", es 1/4, porque una cuarta parte de todas las palabras de código posibles comienza con "01". En general, el costo de las palabras de código disminuye exponencialmente al aumentar la longitud de la palabra de código.



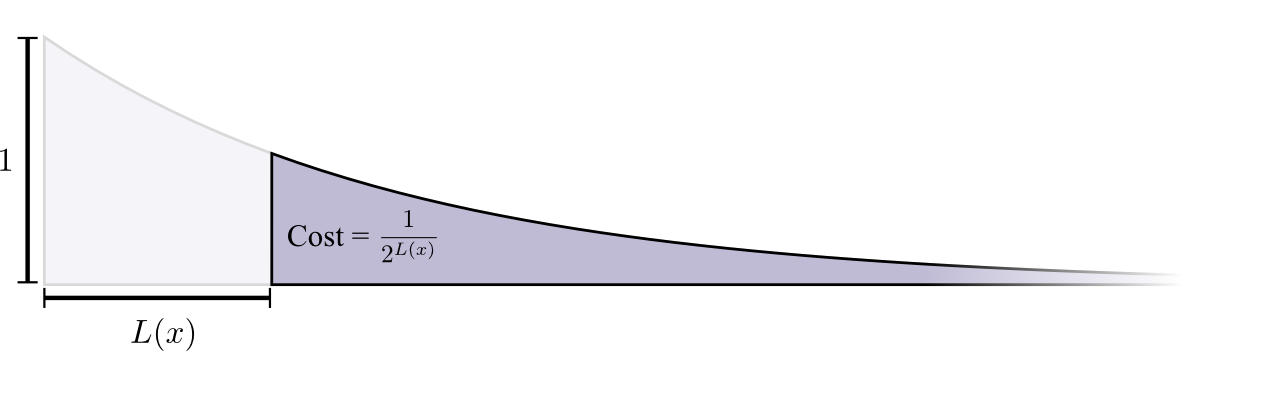
Tenga en cuenta que si el costo disminuye como expositor (en especie), ¡esto es tanto altura como área! ( El ejemplo utilizó un exponente con base 2 donde este hecho es incorrecto, pero puede cambiar al exponente natural, que simplifica visualmente la demostración ) .

Necesitamos palabras de código cortas porque queremos reducir la longitud promedio de los mensajes. Cada palabra de código aumenta la longitud promedio del mensaje por la probabilidad de que esa palabra sea multiplicada por su longitud. Por ejemplo, si necesitamos enviar una palabra de código de 4 bits de longitud el 50% del tiempo, nuestra longitud promedio de mensaje será 2 bits más larga que si no enviamos esta palabra de código. Podemos imaginar esto como un rectángulo.


Estos dos valores están relacionados por la longitud de la palabra de código. El precio que pagamos determina la longitud de la palabra clave. La longitud de la palabra de código determina cuánto se agrega a la longitud promedio del mensaje. Podemos imaginarlos juntos así.



Las palabras de código cortas reducen la longitud promedio del mensaje, pero son costosas, mientras que las palabras de código largas aumentan la longitud promedio del mensaje, pero son baratas.



¿Cuál es la mejor manera de usar nuestro presupuesto limitado? ¿Cuánto deberíamos gastar en una palabra de código para cada evento?

Del mismo modo que una persona quiere invertir más en herramientas que usa regularmente, queremos gastar más en palabras de código de uso común. Hay una manera particularmente natural de hacer esto: distribuir nuestro presupuesto en proporción a la frecuencia con que ocurre el evento. Por lo tanto, si ocurre un evento en el 50% de los casos, gastamos el 50% de nuestro presupuesto en la compra de una palabra de código breve para él. Pero si el evento ocurre solo el 1% del tiempo, gastamos solo el 1% de nuestro presupuesto, porque no estamos muy preocupados por la longitud de la palabra clave.

Esto es algo bastante natural, pero ¿es óptimo? ¡Esto es así, y lo demostraré!

La siguiente prueba es clara y debe entenderse, pero tomará algo de trabajo lograrlo, y esta es definitivamente la parte más difícil de este ensayo. Los lectores pueden saltearlo con seguridad, aceptar el hecho sin pruebas y pasar a la siguiente sección.

Veamos un ejemplo específico donde necesitamos decir cuál de los dos posibles eventos sucedieron. El evento $$un paso$a$$$p ( a ) tiempo y el evento$p(a)$$$b ocurre$b$$$p ( b ) tiempo. Asignamos nuestro presupuesto de la manera natural descrita anteriormente, gastando$p(b)$$$p ( a ) nuestro presupuesto de palabras clave cortas$p(a)$$$$a$ y $$p ( b ) para recibir una palabra de código corta$p(b)$$$$b$ .



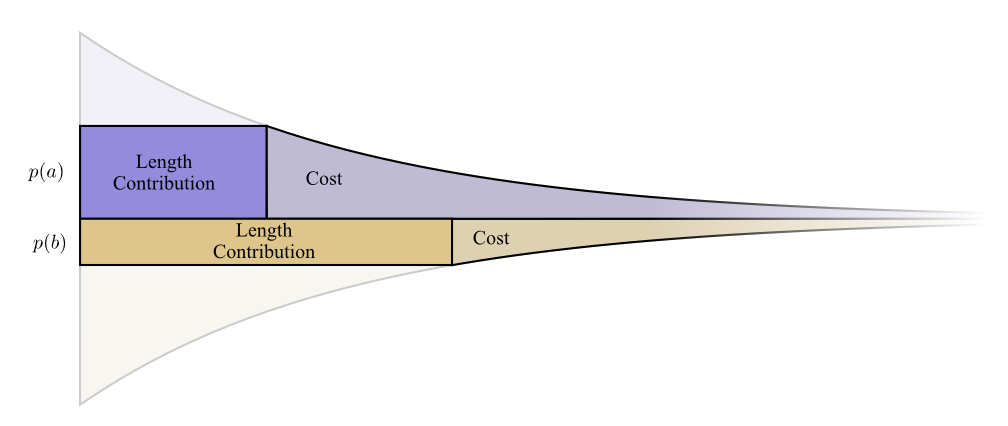Los límites de costo y longitud se alinean maravillosamente. ¿Eso significa algo?

Considere qué sucede con la contribución del costo y la longitud si cambiamos un poco la longitud de la palabra de código. Si aumentamos ligeramente la longitud de la palabra de código, entonces la contribución de la longitud del mensaje aumentará en proporción a su altura en el borde, y el costo disminuirá en proporción a su altura en el borde.



Por lo tanto, el costo de crear una palabra de código más corta es$$$p(a)$ .No nos preocupa igualmente la longitud de cada palabra de código; nos interesan en proporción a la frecuencia con la que las usamos. En caso de$$a es$a$$$$p(a)$ . Nuestra ganancia al hacer la palabra de código un poco más corta es proporcional $$$p(a)$ .

Curiosamente, ambos derivados son iguales. Esto significa que nuestro presupuesto inicial tiene una característica interesante: si tuviera un poco más de dinero, sería igualmente bueno invertir en la reducción de cualquier palabra de código. Lo que realmente nos importa es la relación beneficio / costo: eso es lo que decide en qué deberíamos invertir más. En este caso, la relación$$p ( a )p ( a ) , que es igual a uno. No depende del valor de p (a), siempre es igual a la unidad. Y podemos aplicar el mismo argumento a otros eventos. El beneficio / costo siempre es uno, por lo que tiene sentido invertir un poco más en cualquiera de los eventos. En términos de infinitesimal, cambiar el presupuesto no tiene sentido. Pero esto no es prueba de que este sea el mejor presupuesto. Para probar esto, veremos un presupuesto diferente donde gastamos un poco más en una palabra de código a expensas de otra. Gastaremos en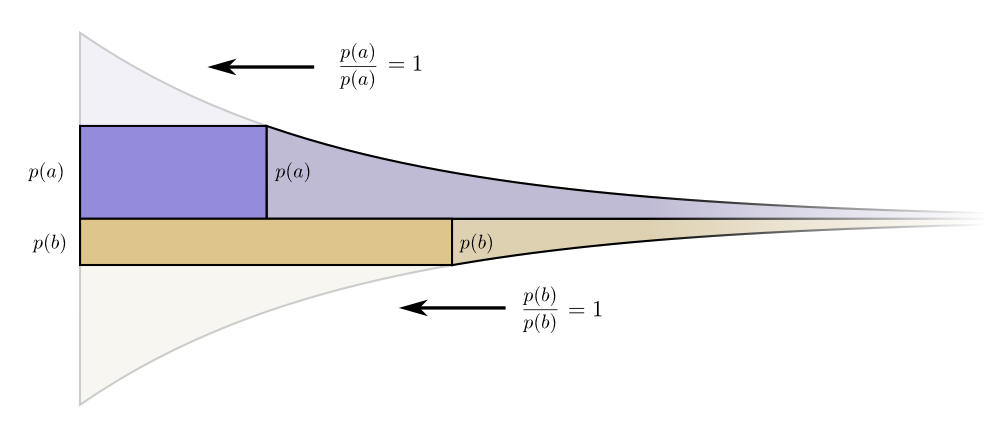$\frac{p(a)}{p(a)}$



$$ϵ menos por$\epsilon$$$b y agregue esto$b$$$ϵ evento$\epsilon$$$$a$ . Hace una palabra de código para $$a es un poco más corto, y la palabra clave para$a$$$b es un poco más largo. Ahora el precio de compra de una palabra de código más corta para$b$

$$a es igual$a$$$p ( a ) + ϵ , y el precio de compra de la palabra de código más corta para$p(a) + \epsilon$$$b es igual$b$$$$p(b) − \epsilon$ .Pero los beneficios son los mismos. Esto lleva al hecho de que la relación costo / beneficio de la compra$$un testamento$a$$$p ( a )p ( a ) + ϵ , que es menos que la unidad. Por otro lado, la relación costo / beneficio de la compra b es$\frac{p (a)}{p(a) + \epsilon}$$$p ( b )p ( b ) + ϵ , que es más de uno. Los precios ya no son equilibrados.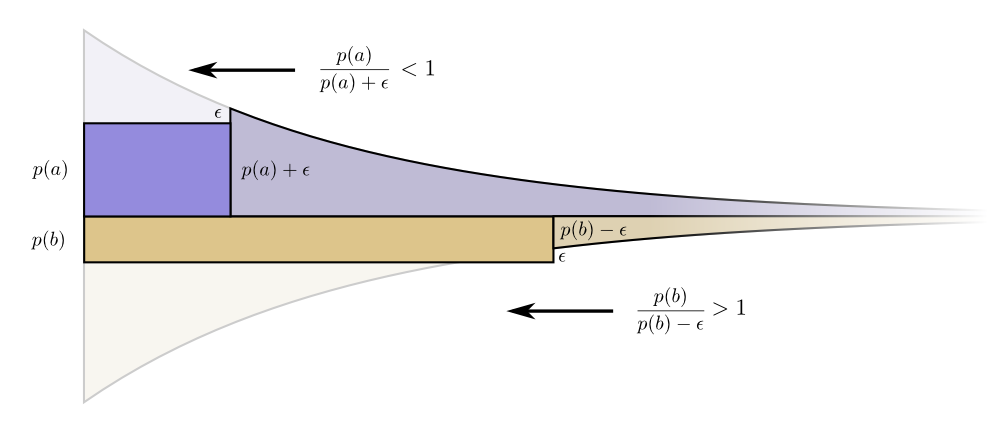$\frac{p (b)}{p(b) + \epsilon}$



$$b mejor trato que$b$$$$a$ . Los inversores gritan: "Comprar $$$b$ ! Vender $$a ! ”Estamos haciendo esto y volviendo a nuestro plan de presupuesto original. Todos los presupuestos se pueden mejorar volviendo a nuestro plan original. El presupuesto inicial, invertir en cada palabra de código en proporción a la frecuencia con que lo usamos, no era solo una opción natural, sino óptima. (Nuestra prueba solo funciona para dos palabras de código; se puede generalizar fácilmente a un número mayor).$a$



(Un lector atento puede haber notado que en el caso de un presupuesto óptimo, pueden aparecer códigos en los que las palabras de código tienen una longitud fraccional. ¿Qué significa esto? En la práctica, si desea comunicarse enviando una palabra de código, tendrá que redondear el valor. Pero, ¿cómo lo hacemos? ver más adelante, ¡hay un sentido real en el envío de palabras de código fraccional cuando enviamos muchas de ellas al mismo tiempo!)

PD La continuación se dedica a la entropía, entropía cruzada, información mutua, bits fraccionales y otras cosas interesantes.